水利水电项目施工风险模糊层次分析以及MATLAB应用

陈伟彬

(广东金松建设集团股份有限公司，广东 佛山 528300)

当前，国内中小型水利水电项目陆续建设并投入使用，尤其是在偏远地区，中小型水利水电项目具有非常重要的作用。但在实际工程建设中，存在着多种不利因素，如施工质量差、机械设备少、工期过短、造价过低、施工图不到位等等，致使工程项目的施工质量受到严重威胁，并且此类风险极易造成损失，不利于工程的建设。如何解决施工风险，并予以有效的预防和控制，是当前亟待解决的问题，建议在解决该问题时应当以风险的划分和分析以及处理为重点。本文利用模糊层次分析理论，采用MATLAB程序建立相应的程序，构建风险评价的相应理论体系,并以实际案例进行分析验证。

1 工程概述

国内某水电站主要利用长度为150 km的大河弯天然落差，再经16 km的引水隧洞，截弯取直而得到水头约300 m。该水电站总装容量为4 800 MW，由拦河闸、引水系统以及地下厂房构成，为引水式水电站。该水电站的主要功能是发电，并兼具蓄能、蓄洪以及拦沙的功能。该工程的投入较高，并且产生的社会影响较大，在施工期内将面临一定的风险。因此，针对该工程进行实际建模，同时分析相应的风险因素，可为施工风险的管理提供一定的科学依据。

2 构建水利工程施工风险评价的模糊层次分析法和MATLAB

模糊层次分析主要基于层次分析为重要基础，经相关专家的调查分析，利用模糊数学对权重进行确定排序，以此来对工程的风险进行评价，实现对风险的有效等级划分，最终明确风险的大小。模糊层次分析最关键的是对权重和风险的划分，以及如何控制计算精度与效率。

2.1 构建递阶层次的结构

根据问题的复杂与分解的程度来得出各个元素，依据不同的属性存在的差异性加以分组，由此建立形成不同层次的相应结构。在同一层次的元素是完全独立的存在，在竖向关系中由上一次所支配，其也能对下一个层次元素进行支配。所以在元素间建立了支配的关系，同时构建出递阶的层次。另外，对于支配关系而言，其可以是完全和不完全的。

2.2 建立判断矩阵

通过建立递阶层次，明确上下级间隶属的关系。假设选择某一次的元素准则设成Ck，相邻的一层元素A1,A2…,An与其为支配关系，同时A1,A2…,An也得到一定的权重。通过利用T.L.Satty 1～9的比例标度来建立标度的矩阵，针对选择的n个元素进行互相的对比来得到判断的矩阵A。

2.3 层次权重排序的计算和检验

权重的计算应当利用数学工具，先构建判断矩阵，并利用线性代数的相关理论知识对特征值加以计算，具体如下：

Aw=λmaxw

(1)

根据式(1)进行计算得出的w，并利用归一化的处理为A1,A2…,An，在Ck下确定权重的相应排序，然后利用系统的分析理论，运用幂法进行计算得到λmax及w。之后开展一致性的计算，一致性CI的计算如下：

(2)

在得到CI以后，与平均随机的一致性指标RI相结合(表1)，再对一致性比例CR的指标进行计算。

表1 平均随机一致性指标

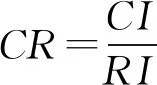
(3)

CR<0.1时，判断矩阵是否存在一致性；反之，应当计算到满足条件为止。

2.4 层次总排序的获取和一致性验证

层次总排序主要是将全部的因素在对总目标的重要程度进行顺序的有效排列；层次总排序权重和层次排序存在不同，其主要指全部因素对总目标的权重。而对层次总排序的计算则使用下述公式：

(4)

式中设定B层存在m个元素，即B1,B2…,Bm，总目标权重b1,b2…,bm；下层对上层的单排序设定为C1j,C2j…,Cnj。

根据上述公式可知，总排序计算应当从最上层进行计算，然后逐步向下层进行计算。

针对总排序一致性的验证则同样是从最上层逐步计算至最下层，计算使用下述公式：

(5)

式中CIj表示下一层C各个元素对B层单排序的一致性指标，RIj则属于随机性的指标。结果显示CR<0.1，判断矩阵是否存在一致性，并通过检验。

2.5 建立因素集和风险因素集

建立拥有多个评价的结果评价集V，具体的向量形式如下：

V={v1,v2,…,vm}

(6)

式中m表示有m个评判结果，决断v1(i=1,2,…,m)则代表不同结果的相关评判，评价主要分成4～5个等级。然后构建因素集，即明确对评价的对象存在影响的n个因素的集合，具体的向量形式如下：

U={u1,u2,…,un}

(7)

2.6 构建隶属度的评价矩阵

通过开展单因素的评判来明确因素集U内每一个因素ui进行相应的评判，再从因素ui中得出此因素对评判级ui的隶属度rij，由此得出单因素的评判集中因素ui:

rij=uj(ui) (j=1,2,…,m)

(8)

从而得到在各因素ui和评价集V间的模糊向量：

ri=(ri1,ri2,…,rim) (i=1,2,…,n)

(9)

通过整合上述各因素间的模糊关系，得出U和V间的模糊关系矩阵，具体如下：

(10)

最后可以依据R来确定项目的风险等级以及大小。

2.7 MATLAB设计

MATLAB主要用在对数据的分析和无线通信以及图像处理等方面，具有非常强大的计算能力，尤其是在计算矩阵方面特别突出。对矩阵的特征值以及特征向量计算可以采用eig函数非常轻松的实现，具体的格式显示为[V,D]=eig(A)。为避免出现复数，运用函数maxeigvalvec.m对V/D结果予以相应的判断。并与MATLAB矩阵计算以及层次分析法的相关特点进行结合，运用sglsortexamine.m函数检验层次分析的单排序一致性，同理对层次分析总排序的权重及一致性进行检验，对tolsortvec.m函数定义后经过计算得以实现。

依据上述对权重及排序的计算，构建模糊隶属矩阵时考虑到操作性和可行性，决定采用专家调查法来构建风险评判表，将专家的人数予进行归一化处理：

(11)

运用矩阵计算开展模糊一级与模糊二级的相应评判，最终对项目工程的风险进行相应的等级判别及划分。

3 应用结果

3.1 层次结构和判断矩阵

对工程施工风险进行分析得出，影响施工风险的主要因素集主要是目标层A(环境因素、施工企业、合同及履约能力、其它因素)，设成B={B1,B2,B3,B4}，并当作第一层(准则层)，而子准则层为第二层，并主要包括16个风险评价的因子(C11-C43)，具体见图1。

依据图1对因素进行对比及评分得出判断矩阵，具体见图2。

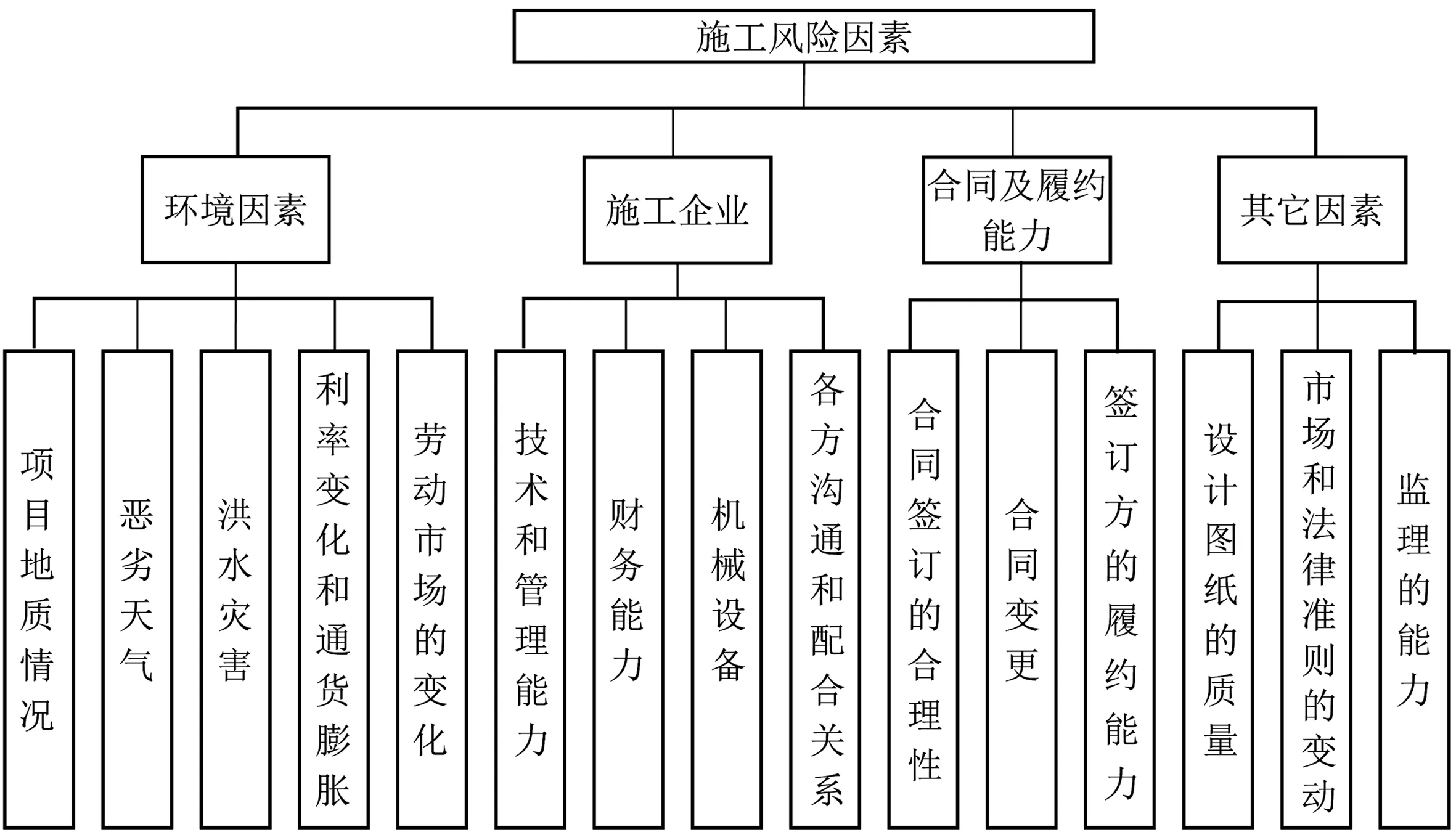
图1 风险影响因素的层次划分

AB1B2B3B4B111/322B23156B31/21/512B41/20/61/21

A-B判断矩阵

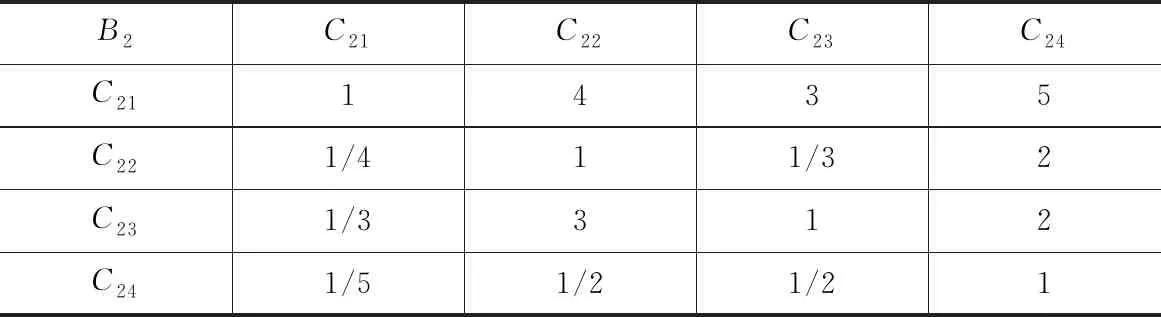
B1-C1i判断矩阵

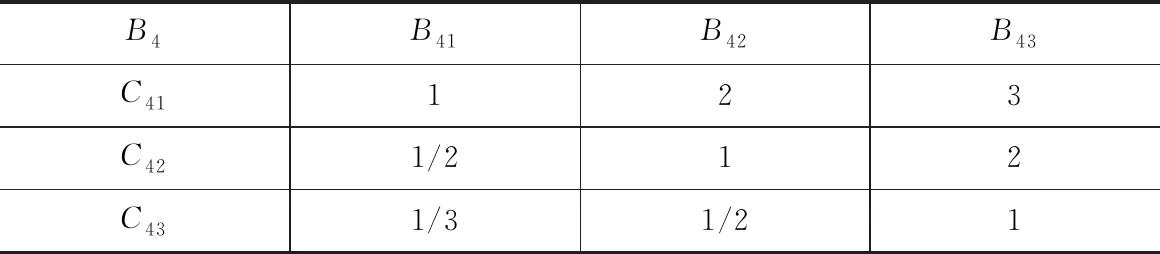
B2-C2i判断矩阵

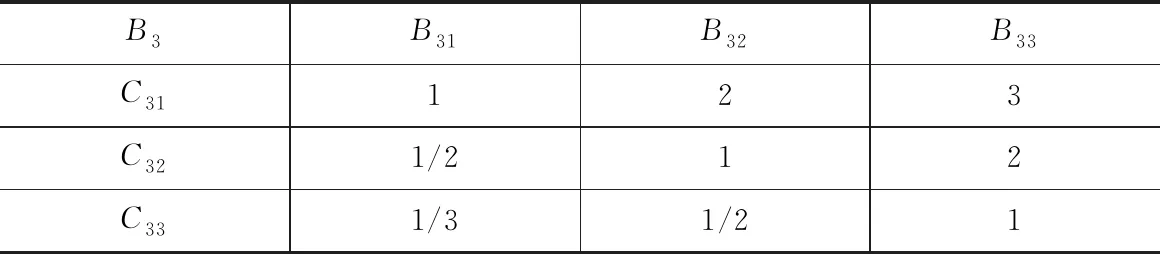
B4-C4i判断矩阵

3.2 层次单排序和总排序以及一致性检验

依据上述判断矩阵来编写主程序main.m，调用子程序maxeigvalvec.m、sglsortexamine.m和tolsortvec.m，运行主程序得出准则层的权重系数：

WA-B=[0.2043 0.5812 0.1282 0.0863]T

WB1-C1i=[0.4683 0.0726 0.0934 0.0617 0.1276 0.1764]T

WB2-C2i=[0.5402 0.1278 0.2391 0.0930]T

WB3-C3i=[0.4934 0.3108 0.1958]T

WB4-C4i=[0.5396 0.2970 0.1634]T

子准则层的权重总排序：

WA-C=[0.0957 0.0148 0.0191 0.0126 0.0261 0.0360 0.3139 0.0743 0.1389 0.0540 0.0633 0.0399 0.0251 0.0466 0.0256 0.0141]T

由此，层次单排序与层次总排序全部通过一致性的检验。

3.3 模糊层次整体风险评价

风险因素集U={环境因素、施工企业、合同及履约能力，其它因素}={C11,C12,C13,C14,C15,C16,C21,C22,C23,C24,C31,C32,C33,C41,C42,C43}，风险评价集V={严重、较高、一般、较小、轻微}。表2为8名本领域专家制定的风险评判表。

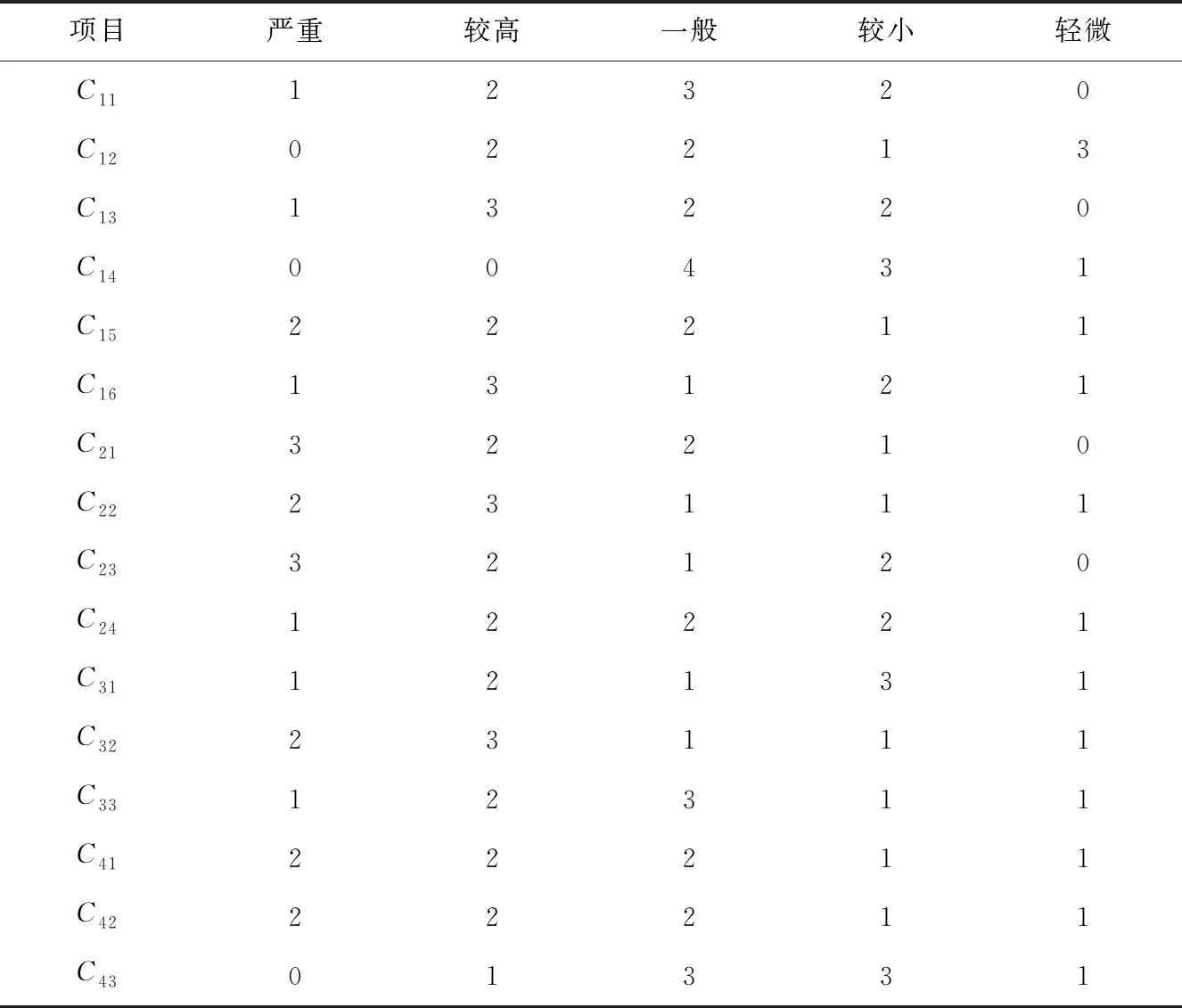
表2 工程施工风险评判

利用式(11)可以得出表2中风险隶属的矩阵R1、R2、R3、R4。根据模糊层次评判原理，得出目标层的环境因素、施工企业、合同及履约能力及其它因素的模糊矩阵：

Y1=C1R1=[0.0253 0.0548 0.0617 0.0475 0.0149]

Y2=C2R2=[0.1972 0.1559 0.1269 0.0974 0.0160]

Y3=C3R3=[0.0210 0.0371 0.0223 0.0319 0.0160]

Y4=C4R4=[0.0181 0.0198 0.0233 0.0143 0.0108]

依据最大隶属度的相关原则得出：环境因素的风险Y1∈v3，表明程度一般；施工企业风险因素Y2∈v2，表明程度较高；合同及履约能力风险因素Y3∈v2，表明程度较高；其它因素Y4∈v3，表明程度一般。

根据一级模糊评判结果Y1,Y2,Y3,Y4，建立二级模糊评判矩阵隶属矩阵R，依据计算得出二级模糊评判矩阵：

Y二级=B二级Y一级=[0.1240 0.1083 0.0912 0.0716 0.0153]

依据最大隶属度的相关原则得出二级模糊的评判结构为：水电站的施工风险Y∈v1，表明施工的风险严重。分析主要原因可能是该工程从业主到施工的实施中出现违规的行为，导致施工风险非常严重，并与实际的工程情况相符。

4 结 论

模糊层次分析法是一种定性及定量的分析方法，既能对风险进行识别，也能对风险进行评价。在一些多层次分析中，运用近似法对计算精度有严重影响，而利用MATLAB程序能够方便地求出矩阵特征值和向量，并且具有较高的精度以及效率。根据上文的分析结果得出以下结论：

1) 以模糊层次的分析原理为基础，利用MATLAB程序软件编写计算的主要程序，进一步提升了计算的精度及工作效率，避免运用近似方法求解矩阵最大特征值与特征向量。

2) 通过对某水电工程为实际案例进行分析，运用模糊层析分析及MATLAB程序结合，对工程施工的风险因素予以相应的评价，进一步揭示了因素的风险程度，并进行了相应的划分。由此表明，该方法具有较高的可行性及科学性，可以明确施工风险的程度。