关于网的理想收敛性质

熊 倩

（闽南师范大学数学与统计学院,福建漳州363000）

统计收敛是一般收敛的推广,它的思想可以追溯到Zygmund[1]的专著.1951年,Fast[2]和Steinhaus[3]基于正整数集的子集的渐近密度提出实数序列的统计收敛概念.直到Šalát[4]的工作,特别是Fridy[5-6]的论文之后,关于统计收敛的研究开始变得活跃起来,越来越多研究者对它进行了推广研究.特别是Di Maio 和Kocinac[7]于2008年提出了拓扑空间及一致空间中统计收敛的概念,并研究了它的性质及应用.此外,统计收敛也在数学其他分支中出现,如：可和性理论[8],数论[9],三角级数[1],概率论[10],最优化[11],测度论[12],逼近论[13]等,具有非常广泛的应用价值.

理想收敛是统计收敛的推广.Kostyrko 等[14]利用正整数集上理想的概念引入了序列的理想收敛,并在度量空间中研究了它们的相关性质.随后Šalát 等[15-16]将统计收敛的一些概念和结果推广到理想收敛,并与可和性理论联系起来.除了理想收敛之外,I*收敛也是统计收敛的有趣推广.2005年,Lahiri等[17]将理想收敛和I*收敛的概念推广到一般的拓扑空间中, 并研究了它们的一些性质. 其后Tripathy 和Hazari‐ka[18-20]从函数、收敛域等不同方面研究了理想收敛的相关性质.最近周先耕等[21]、林寿[22]研究了由理想收敛定义的一些拓扑空间以及在这些空间上的映射和相关性质.在过去20年里,许多学者在理想收敛和相关问题上做了大量工作,使其成为拓扑学和分析学中最活跃的研究课题之一[23].

最近,Hazarika[24]在第一可数的拓扑群中研究了序列理想收敛的若干运算性质.Das[23]证明了以下结果：设I是ℕ 的一个可容理想,1)C(I)是l∞的闭线性子空间；2)其中l∞为ℝ 中全体有界序列的集合且赋予上确界范数,C(I)和C(I*)分别为ℝ中全体I收敛和I*收敛的有界序列.

网作为序列的推广,在一般拓扑中具有重要意义[25].本文围绕Hazarika[24]和Das[23]的工作,首先讨论了拓扑群中网的理想收敛的运算性质,获得了如下结果：设G是拓扑群,(xα)α∈D及(yα)α∈D是G中的网, 1)若I- limxα=x0及I- limyα=y0, 则I- limxαyα=x0y0; 2) 若I- limxα=x0, 则I- limxα-1=x0-1; 设G是满足第一可数公理的拓扑群,I是D上的P理想.若G中的网理想收敛于x,则存在G中的网及满足limyα=x,xα=yα zα,{α∈D:xα≠yα} ∈I且{α∈D:zα≠e} ∈I.其次在Βanach 空间中定义了lD∞及其C(I)和C(I*),并讨论了lD∞中C(I)和C(I*)的相关性质,获得了如下结果：若I是D可容理想,则1)C(I)是lD∞的闭线性子空间;2)这些结果推广了Hazarika和Das的相关工作.

1 预备知识

定义1[26]称集合D是一定向集,若对D的某些元素规定了次序＞并满足以下条件：1)若a＞b及b＞c,则a＞c;2)对任意a,b∈D,存在c∈D,使得c＞a及c＞b.

定义2[23]令(D,＞)是一定向集,X是一非空集,映射s:D→X称为X上的网,记为(sα:α∈D,＞)或（也可简记为(sα)）.网(sα)称为终留于A⊂X,若存在α∈D,使得对任意β∈D且β＞α,有sβ∈A.拓扑空间(X,τ)中网(sα)称为收敛于x∈X,若(sα)终留于x的每一个邻域,即对x的任意邻域U,存在β∈D,使得对任意α∈D且α＞β时有sα∈U,记作limsα=x.

定义3[23]非空集族I⊆2D(D的幂集)称为D的理想当且仅当满足以下条件：1) 对任意A,B∈D, 有A⋃B∈D; 2) 对任意A∈D且B⊂A, 有B∈D. 理想I称为非平凡, 若I≠{∅ } 且D∉I. 集族（I）={D-A:A∈I} 称为理想I的导出滤子.设D为非空定向集,对于α∈D,定义Dα={γ∈D:γ≥α} ,称D的非平凡理想I为D可容,若对任意α∈D,有Dα∈（I）.

定义4[23]设X是拓扑空间,(sα)是X中的网,则有：

1)(sα)称为I收敛于x∈X,若对包含x的任意开集U,有{α∈D:sα∉U} ∈I,记作I- limsα=x;

2)(sα)称为I*收敛于x∈X,若存在集M∈（I）使得M是定向集且网(sα)α∈M收敛于x,记作I*-limsα=x.

定义5[23]D可容理想I称为满足条件(DP)(或称为P理想),若对两两不交的集族{Ai}i∈ℕ⊂I, 存在集族使得对任意j∈ℕ,存在αj∈D,有AjΔBj⊂DMαj且B=∪Bj∈I.其中对任意j∈ℕ,Bj∈I.

定义6[27]设G是群,τ是群G上的一个拓扑.称(G,τ)是半拓扑群,如果对于群G上任意一个元在G中的左乘法运算和右乘法运算都是连续的;称(G,τ)是仿拓扑群,如果群G上的乘法运算是共同连续的;称(G,τ)是拟拓扑群,如果(G,τ)是半拓扑群且群G上的逆运算是连续的;称(G,τ)是拓扑群,如果(G,τ)是仿拓扑群且群G上的逆运算是连续的.

引理1[23]设I是D可容,X是拓扑空间,是X中的网, 则有：1) 若limxα=x, 则I- limsα=x; 2) 若I*- limsα=x,则I- limsα=x.

引理2[23]若I是P理想, 且X是第一可数拓扑空间. 对X中的任意网(sα), 若I- limsα=x, 则I*-limsα=x.

本文ℕ 表示正整数集,D为非空定向集,所涉及的理想I均是D可容理想,对一些未说明的定义和术语可以参考文献[23-27].

2 主要结果

2.1 拓扑群中网的理想收敛

定理1设G是拓扑群,(xα)α∈D及(yα)α∈D是G中的网.若I- limxα=x0及I- limyα=y0,则I- limxαyα=

证明设νe是单位元e的全体开邻域形成的集族.因为G是拓扑群,从而G上的映射φ:G×G→G连续, 即有φ:(x,y)↦x0xy0y连续, 且有φ(e,e)=x0ey0e=x0y0. 因此对任意V∈νe, 存在V1,V2∈νe使得(x0V1)(y0V2)⊂x0y0V.因为I- limxα=x0,从而由定义4 知{α∈D:xα∉x0V1} ∈I.同理有,{α∈D:yα∉y0V2} ∈I.因此由(x0V1)(y0V2)⊂x0y0V知,

又由上式右边均属于I,因此{α∈D:xαyα∉x0y0V} ∈I,即证I- limxαyα=x0y0.

定理2设G是拓扑群,(xα)α∈D是G中的网.若I- limxα=x0,则I- limxα-1=x0-1.

证明设U是单位元e的任意开邻域. 因为G是拓扑群, 从而存在e的开邻域V满足V=V-1且xVx-1⊂U,即Vx-1⊂x-1U.因为I- limxα=x0,由定义4知{α∈D:xα∉x0V-1} ∈I,即{α∈D:xα-1∉Vx0-1} ∈I.故由Vx-1⊂x-1U知,{α∈D:xα-1∉x0-1U} ⊂{α∈D:xα-1∉Vx0-1} .因此{α∈D:xα-1∉x0-1U} ∈I,即证I-limxα-1=x0-1.

注定理1对仿拓扑群也成立,定理2对拟拓扑群也成立.

定理3设G是满足第一可数公理的拓扑群,I是D上的P理想.若G中的网(xα)α∈D理想收敛于x,则存在G中的网(yα)α∈D及(zα)α∈D满足limyα=x,xα=yα zα,{α∈D:xα≠yα} ∈I且{α∈D:zα≠e} ∈I.

证明因为I是P理想,则由引理2知网(xα)α∈DI*收敛于x,从而存在集使得M是定向集且网收敛于x.对任意α∈D,若α∈M,则令yα=xα且zα=e;若α∉M,则令yα=x且zα=x-1xα.因此,对任意α∈D,有

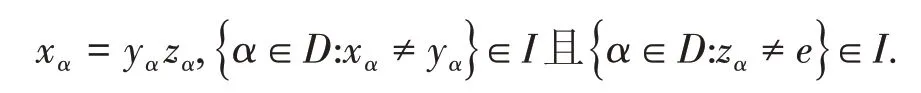
下证limyα=x.事实上,因为网(xα)α∈M收敛于x,则对x的任意邻域U,存在β∈M,使得对任意α∈M且α＞β时有xα∈U.由上述构造知,对任意α∈D且α＞β时有yα∈U,因此limyα=x.

2.2 Βanach空间中网的理想收敛

每一个Βanach空间是拓扑群,接下来讨论Βanach空间上全体有界的理想收敛网的性质.为了下面的应用，给出Βanach空间中网的理想收敛的相关定义.

定义7设D为非空定向集,I为D上的理想，X为Βanach空间,(sα)是X中的网.

1)(sα)称为I收敛于x∈X,若对任意ε＞0,有记作I- limsα=x;

2)(sα)称为I*收敛于x∈X, 若存在集使得M是定向集且网收敛于x, 记作I*-limsα=x.

设X是Βanach 空间,令分别为X中全体I收敛和I*收敛的有界网,由定理1,定理2及Βanach空间的性质,易知是线性空间.赋予上确界范数

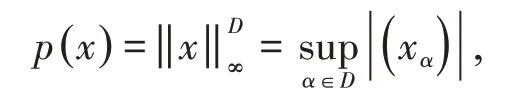
定理41)C(I)是lD∞的闭线性子空间;

证明1) 令其中x=(xα)α∈D. 下证x∈C(I).

断言1(ξm)是X中的柯西序列.

对任意η＞0,由limx(m)=x可知存在m0∈ℕ,使得对任意u,v≥m0,有固定u,v＞m0,由假设注意到从而

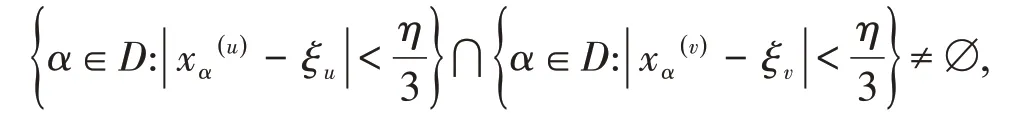
即存在s∈D,有故

因此(ξm)是X中的柯西序列,又因为X完备,从而(ξm)收敛,令limξm=ξ∈X.

断言2(xα)α∈D理想收敛于ξ.

对任意ε＞0,因为limξm=ξ,则存在v0∈ℕ,使得当m＞v0时有同时当m＞v0时也会满足故对任意α∈D有

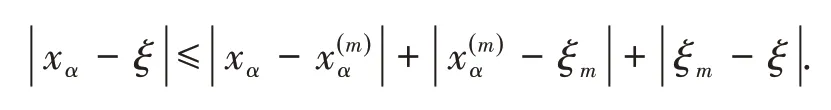
2)因为I是D可容理想,由引理1有C(I*)⊂C(I),又由结论1)知C(I)在lD∞中是闭的,故得

因为y∈C(I),令A=I- limy. 由定义7 知, 对包含A的任意开集U, 有{α∈D:yα∉U} ∈I, 记G={α∈D:yα∉U} .定义网x=(xα)如下：若α∈G,则xα=yα;否则xα=A.由构造易知x∈lD∞.因为当α∈DG时,DG∈F（I）,且此时xα=A,由定义7 知I*- limx=A成立, 即x∈C(I*). 对任意η∈( 0,δ), 当α∈G时,有恒成立;当α∈DG时,η＜δ.于是有因此有证毕.