细分析,巧变换,妙求值
2021-06-29 07:44夏晓静
中学生数理化·高一版 2021年6期
■夏晓静
三角函数的求值问题是每年高考的必考内容。解答这类问题,可利用“平方关系式”“和角公式”“倍角公式”等进行变换求值。下面对“变式、变角与变名”等方法在解题中的运用加以归纳,希望对同学们解决三角函数求值问题有所帮助。
一、观察结构,通过“变式”,求三角函数的值
例1 已知sinα+cosβ=1,cosα+sinβ=0,则sin(α+β)=_____。
分析:将所给的两个等式分别两边平方,借助sin2α+cos2α=1即可得到结果。
解:已知两个等式的两边分别平方可得

评析:观察所给等式的结构特征,发现具有轮换对称关系,利用“两边平方”相加,可得到所求三角函数的值。

二、分析角度,依据“变角”,求三角函数的值
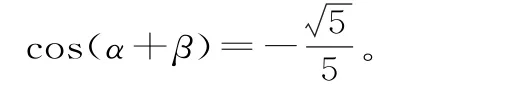
(1)求cos2α的值。
(2)求tan(α-β)的值。
分析:(1)利用已知角α,可求出cos2α的值;(2)把所求角α-β转化为2α-(α+β)求解。

评析:此题属于求三角函数值中的“给值求值”型,解题的关键是要找到已知角与所求角之间的关系,从而达到解题的目的。


三、紧扣函数名称,尝试“变名”,求三角函数的值
例3 求(tan10°-3)·sin40°的值。分析:利用“切化弦”及特殊角的三角函数求值。
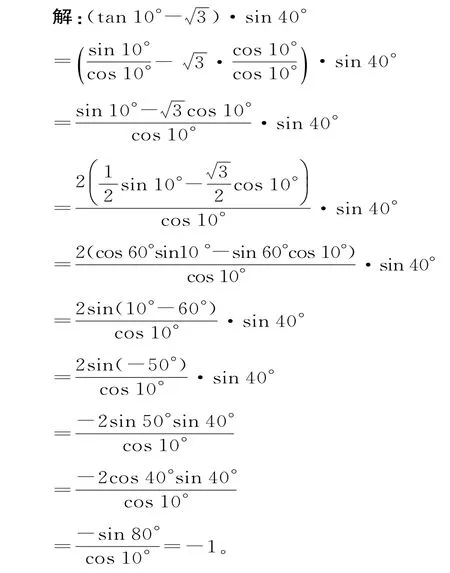
评析:利用“切化弦”将函数名称统一为正弦和余弦,再引入辅助角公式,可将问题化简到底。本题属于“给角求值”型,题中给出的角都是非特殊角,通过寻找非特殊角与特殊角之间的关系,从而达到求值的目的。

提示:因为5sin(α+2β)=7sinα,所以5sin(α+β+β)=7sin(α+β-β)。
由两角和与差的正弦公式可得5sin(α+β)cosβ+5cos(α+β)sinβ=7sin(α+β)cosβ-7cos(α+β)sinβ,即sin(α+β)cosβ=6cos(α+β)sinβ,其中cosβ,cos(α+β)均不为0。
上述方程两边同除以cosβcos(α+β),可得tan(α+β)=6tanβ。故原命题成立。

猜你喜欢
新高考·高三数学(2022年3期)2022-04-28
读写月报(初中版)(2021年12期)2021-05-25
数学小灵通(1-2年级)(2020年9期)2020-10-27
新高考·高一数学(2018年5期)2018-11-22
黄河之声(2016年24期)2016-02-03
读写算(中)(2015年11期)2015-11-07
电测与仪表(2015年16期)2015-04-12

