波浪与地震荷载共同作用下桩的动力响应

刘晨晨，张 琪，李明广，周香莲，黎蔚杰

(上海交通大学 海洋工程国家重点实验室； 土木工程系， 上海 200240)

随着传统能源的大量消耗，越来越多的国家开始可再生能源的发展与使用.风能是一种清洁高效的能源，在沿海地区的储备极其丰富.基于成本与技术的考虑，大部分海上风机基础采用的是单桩基础.对于我国而言，海岸线绵长，海上风能资源十分丰富，但大多处于地震烈度较高的地区，海上风机不仅会受到波浪荷载的循环作用，同时也面临着地震破坏的风险.因此，在海上风机单桩基础设计过程中，为确保结构安全性，需充分考虑波浪荷载与地震荷载等复杂的海洋环境荷载对于桩基的影响.

近年来，许多学者对于地震荷载作用下桩基的动力响应问题进行了大量研究.其中，刘宗贤等[1]对分层弹性地基中的单桩基础按Winkler模型进行了特性分析，给出了桩基础横向自振特性及在横向动力与地震荷载作用下的解析解.Kjørlaug等[2]研究了海上风机单桩基础在水平地震与竖向地震作用下的动力响应问题，在他们的研究中，桩对于地震加速度具有一定的放大效应，桩顶的加速度放大系数为2.吴小峰等[3]研发了初始水平环境施加装置，设计了砂土地基中的近海风机单桩基础超重力动力模型试验，从物理模型尺度上初步实现了考虑初始水平环境荷载与地震荷载联合作用的单桩基础动力试验.

对于海上风机单桩基础受波浪荷载作用时的动力响应及其与海床相互作用的问题，学者们进行了大量研究.其中，Lu等[4]提出了一种耦合模型，用于研究波浪荷载作用下多孔海床和海上单桩的动力响应问题，他们将波浪力考虑为一种外荷载，并在线性波浪理论的背景下，通过波函数展开法进行计算.Sui等[5]采用完全非线性Boussinesq方程模拟了波浪与桩的相互作用，发现单桩基础对于波浪运动以及孔隙水压力响应具有重要影响.李琪等[6]基于COMSOL有限元软件计算分析台风环境中风机结构承受的风荷载、波浪荷载和流荷载,建立典型大直径单桩与导管架基础风机结构简化模型,分析了台风极端工况下风机桩基泥面和轮毂点的转角与位移动态响应.

本文基于Abaqus有限元软件建立了一个三维单桩基础有限元模型，分别考虑了地震荷载单独作用下以及地震荷载与波浪荷载共同作用下单桩的动力响应问题.其中地震荷载以Kobe地震波水平加速度时程曲线作为地震输入，作用在桩上的波浪力采用Morison方程进行简化模拟.并进一步分析讨论了桩的弹性模量、埋深以及土体弹性模量对于单桩动力响应的影响.

1 数值方法

1.1 隐式动力分析

为研究波浪荷载与地震荷载共同作用下桩基动力响应问题，本文采用隐式动力分析方法.隐式积分方法基本假设如下：

(1)

(2)

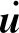
(3)

(4)

将式(3)、(4)代入t+Δt时刻平衡方程，则有：

(7)

1.2 波浪理论

本文中波浪运动采用线性波浪理论进行描述，其表达式如下：

(8)

式中：φ为速度势；H为波高；k为波数，k=2π/Lw，Lw为波长；T为波浪周期；z竖向坐标；d为水深；x为水平坐标；ω为波浪圆频率，ω=2π/T.

波面方程表达式如下：

(9)

(10)

(11)

1.3 Morison方程

Morison等[7]提出Morison方程，用于计算波浪荷载作用在结构物上产生的力.目前，与波长相比尺度较小的细长柱体波浪力计算在工程中仍采用Morison方程.一般认为，桩直径与波长的比值，即D/Lw<0.2(D为桩身直径)的柱体为小尺度结构物，适用于Morison方程.根据Morison方程理论，作用在结构物的波浪荷载包括拖曳力和惯性力两个部分.拖曳力及惯性力在时域中表示为

(12)

式中：f为单位长度上作用的波浪力；fD、fI分别为单位长度上作用的拖曳力和惯性力；ρ为海水密度；CD为拖曳力系数；CM为惯性力系数.

将式(9)、(10)代入式(12)并积分可得到水平波浪力表达式如下：

|cos (kx-ωt)|+

(13)

式中：g为重力加速度，

本文中，波浪力作为集中力施加在桩上.

2 计算模型

2.1 模型设置

本文采用通用有限元软件Abaqus建立桩-土模型，并对地震荷载与波浪荷载共同作用下桩的动力响应规律进行研究.为更加真实地模拟地震荷载与波浪荷载作用下桩-土动力响应，本文假定土体为Mohr-Coulomb模型，桩为弹性材料.

桩-土之间接触面采用主从接触，刚度较大的桩设为主面，刚度较小的土设为从面.法向接触采用硬接触，切向接触采用库伦摩擦模型，具体表述如下：

τc=μP

(14)

式中：τc为接触面发生滑移时的临界切应力；μ为摩擦因数；P为接触面之间的接触压力.

在桩-土动力相互作用中，土体与桩基础中均存在阻尼.本文仅考虑土体的阻尼，忽略桩的阻尼.土体材料阻尼采用瑞利阻尼理论：

C=αM+βK

(15)

式中：α及β均为阻尼系数，

(16)

ω1、ω2分别为土体一阶、二阶自振频率，ξ为阻尼比，取值5%.

2.2 边界条件

本文中，竖向边界允许产生水平位移，约束竖向位移，并对竖向边界采用图1所示的约束压力，以模拟土体真实环境，且在地震过程中，约束压力假定不变.地震波通过水平加速度的形式添加在模型底部x方向，约束压力计算式为

图1 边界条件Fig.1 Boundary conditions

Ps=K0ρsgzs=(1-sinσn)ρsgzs

(17)

式中：K0为静止土压力系数；ρs为土体密度；zs为土体深度；σn为摩擦角.

3 模型验证

在模型研究之前，对地震荷载作用下桩的动力响应进行验证，参考Peiris等[8]的数值模型.其中，桩的尺寸为0.25 m×0.25 m，弹性模量为36 GPa，泊松比为0.15，桩贯穿整个土体.土体为成层土，分为5层，总厚度33 m，各层具体参数如表1所示.地震波采用峰值加速度为0.1g的Northridge地震波.图2为地震波作用下桩顶水平位移u随时间变化结果的对比.可以看出，本文模型的数值结果与Peiris等人的计算结果基本一致.因此，本文建立的桩-土三维模型能够比较好地反映桩在地震作用下的动力响应情况.

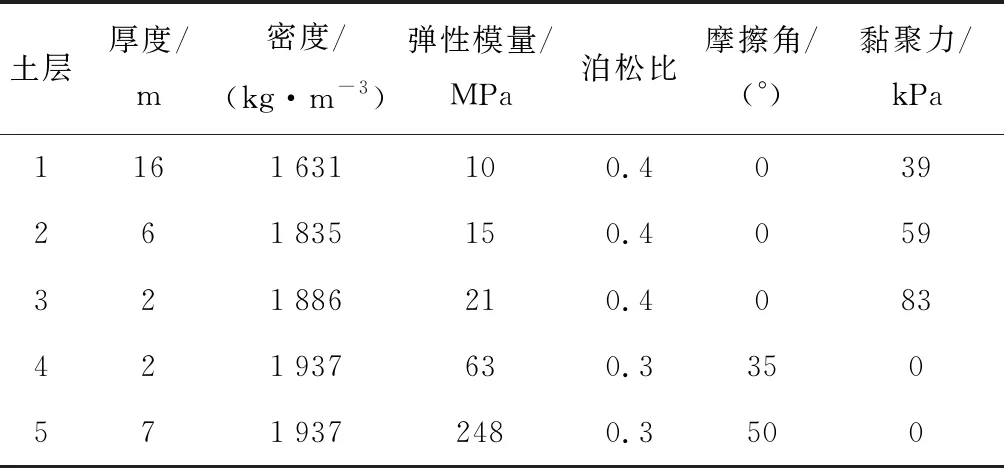
表 1 Peiris模型参数Tab. 1 Parameters of Peiris’ model

图2 地震荷载验证Fig.2 Verification for seismic load

4 数值结果和讨论

本文建立了一个三维桩-土有限元模型，以研究波浪荷载与地震荷载共同作用下桩的动力响应问题.桩的网格尺寸为0.25 m，土单元的网格尺寸为0.25～2 m，时间步为0.02 s.土、桩和波浪的相关参数如表2所示.输入地震波采用峰值加速度为0.1g的Kobe地震波，其时程曲线如图3所示, 图中aK为加速度.为了进一步研究地震荷载与波浪荷载共同作用下桩的动力响应问题，本节将讨论桩的弹性模量Ep、埋深db、直径D以及土体弹性模量Es的影响.

图3 Kobe地震波Fig.3 Kobe earthquake

表2 模型参数Tab.2 Parameters of the model

4.1 不同荷载组合时桩顶动力响应

图4比较了地震荷载单独作用时和地震与波浪荷载共同作用下时桩顶的动力响应情况.图中ah和uh分别为桩顶水平加速度和桩顶水平位移.从图4(a)可以看出，波浪荷载对于桩顶水平加速度的影响相对较小.对于桩顶水平位移，波浪荷载与地震荷载共同作用时的桩顶水平位移相较于地震荷载单独作用时略有增加，但总的来看波浪荷载的影响相对较小.

图4 不同荷载条件下桩顶动力响应Fig.4 Dynamic response of head of pile under different load conditions

4.2 桩的弹性模量

基于表格2中模型参数，本节考虑Ep=2,20,100 GPa时桩的动力响应.图5表示具有不同弹性模量的桩受到波浪荷载与地震荷载共同作用时桩顶动力响应.桩顶加速度动力响应受桩的弹性模量影响较大，弹性模量越大，加速度越小.桩顶水平位移受弹性模量影响更为显著，当Ep=2 GPa时，在地震与波浪共同作用下，桩顶水平位移明显大于Ep为20和100 GPa时的桩顶水平位移，且Ep=20,100 GPa时桩顶水平位移相差不大.值得注意的是，在荷载作用在桩的初期，尤其是Ep=2 GPa时，波浪荷载起主要作用.

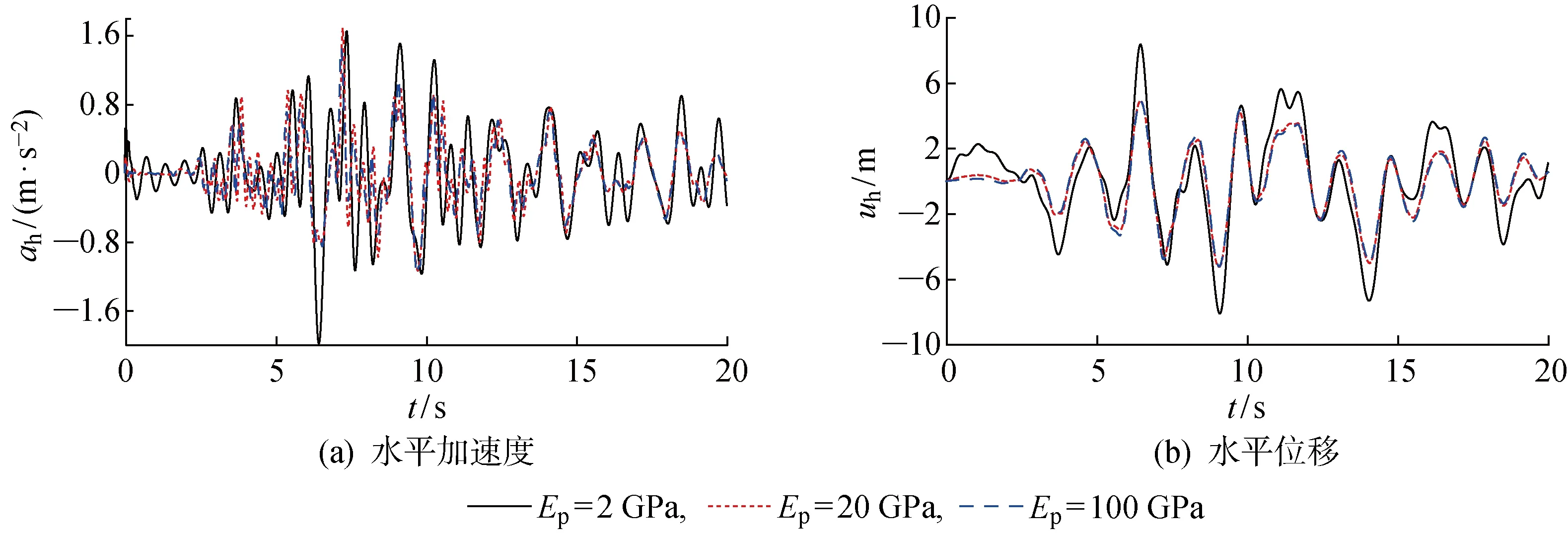
图5 不同弹性模量时桩的桩顶动力响应Fig.5 Dynamic response of head of pile with different elastic modulus of pile

为了更加直观地表示桩的弹性模量对于动力响应的影响，图6绘制出了t=9.06 s时的桩身相对加速度变化以及t=6.48 s时的桩身相对位移变化.图中：h为桩身高度，桩顶为原点，向下为正；ar和ur分别为桩身相对水平加速度和相对水平位移.可以看出，埋置部分的桩受桩的弹性模量影响较小，而露出部分影响较大.

图6 不同弹性模量时桩沿桩身动力响应Fig.6 Dynamic response along pile with different elastic modulus of pile

4.3 桩的埋深

桩的埋深是影响桩的动力响应的一个重要因素，为研究桩的埋深的影响，本节研究了3种情况下桩的动力响应情况，分别为埋深16、18及20 m.图7(a)、7(b)分别表示不同埋深条件下桩顶的加速度动力响应变化与水平位移动力响应变化.如图7(a)所示，桩埋深越大，桩顶的加速度动力响应越小.类似地，图7(b)中桩顶水平位移随着埋深的增加而减小.

图7 不同埋深时的桩顶动力响应Fig.7 Dynamic response of head of pile at different buried depths

图8为加速度响应与水平位移响应沿桩身的变化情况.可以看出，埋置部分的桩的加速度与位移变化规律同露出部分有显著差别，埋置部分的桩的相对加速度随着埋深的增加而增加，而露出部分则完全相反.对于相对位移，埋置部分的桩的相对位移也随着埋深增加而增加，露出部分随着埋深增加而减小.由此表明，海床土体对于桩会有约束效应，能够在地震发生时对于桩产生一定的保护作用.埋深越大时，这种保护作用越大.

图8 不同埋深时沿桩身动力响应Fig.8 Dynamic response along pile at different buried depths

4.4 土的弹性模量

本节研究土体弹性模量对于桩的动力响应的影响，基于表2的参数，考虑Es=40,80,120 MPa的3种情况.图9比较了3种情况下桩顶的加速度动力响应变化与水平位移响应变化.总体而言，桩顶加速度随着土体弹性模量的增加而减小；土体弹性模量越小，桩顶水平位移越大.如图10所示，土体弹性模量对于相对加速度与相对位移沿着桩身的变化有着显著影响.尤其当Es=120 MPa时，桩身的相对位移几乎为0.

图9 土的弹性模量不同时的桩顶动力响应Fig.9 Dynamic response of head of pile with different elastic modulus of soil

图10 土的弹性模量不同时沿桩身动力响应Fig.10 Dynamic response along pile with different elastic modulus of soil

5 结论

(1) 相较于地震荷载对于桩的影响，波浪荷载影响相对较小.在地震荷载作用下，桩身对于地震加速度具有一定的放大效应.

(2) 在其他条件相同的情况下，随着桩的弹性模量的增加，加速度响应与位移响应均随着弹性模量的增加而减小.埋置部分的桩受桩弹性模量的影响较小，而露出部分影响较大.

(3) 桩顶加速度随着土体弹性模量的增加而减小.土体弹性模量越大，桩的水平位移越小.土体对于桩的约束作用随着土体弹性模量增加而增强.