基于多种预测模型的人均可支配收入预测研究——以苏州市城镇居民为例

陈懋昕，邓霓冉

（苏州大学 政治与公共管理学院，江苏 苏州 215123）

自改革开放以来，民生问题一直是党和国家最为关心的，党的十九大把提高人民收入水平作为逐步实现全体人民共同富裕目标的重要内容。苏州市经济运行稳健，改革扎实推进，可支配收入数据不仅是衡量苏州市居民生活水平的基本指标，对其发展成果的检验，对苏州市政府经济政策的制定也有着重要的作用。对人均可支配收入的分析预测一直是一些专家学者的重要研究内容，李新朋（2019年）对1985—2017年上海市城镇居民人均可支配收入的数据运用SAS软件建立ARIMA（1,1,0）的拟合模型。张钊（2018年）利用1992-2017年贵州城乡可支配收入差距数据，建立了指数曲线预测模型与ARMA模型的组合模型。构建了GIOWA算子优化组合预测方法。可以看出除了单一的预测模型外，组合预测也得到了广泛运用。本文以苏州市城镇常住人民可支配收入为例，运用多种单一预测方法和组合预测方法建立预测模型，并从中寻求最优模型。

1.数据来源与研究方法

1.1 数据来源

基于可操作性及数据准确性考虑，通过查阅苏州市统计年鉴（2019）官方数据，收集了从1989年到2018年共30年城镇常住居民人均可支配收入的历史数据，并绘制成以时间编号为横轴，收入（单位：千元）数据为纵轴的时间序列图。

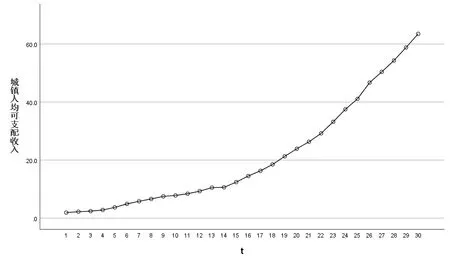
图 1 苏州城镇居民人均可支配收入时间序列图

1.2 研究方法

1.2.1 三次指数平滑法料对本期的意义较小， 当时间序列的变动表现为二次曲线趋势时，则需要用三次指数平滑法。其计算公式为：

三次指数平滑法的预测模型为

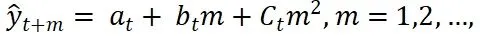
1.2.2 趋势外推法

趋势外推法是依据预测目标的历史数据，提示其发展变化规律，常用的趋势预测模型有多项式模型、指数曲线预测模型等。曲线拟合优度有专用的测量方法：

R²取值在0～1之间，R²越接近1，说明回归方程对于样本数据点的拟合优度越高；反之，R²越接近0，说明回归方程对于样本数据点的拟合优度越低。

1.2.3 组合预测模型

组合预测模型是指把多种预测方法所得到的预测结果进行综合，假设对某一问题有k(k>1,且k为整数)种预测模型，经过具体的权重确定方法得到第i种预测模型的权重wi(i=1,2,…,k)，此时组合预测模型就可表示为：

式中：

1.2.4 预测精度评价

为不同模型的预测精度，选取了以下3 种误差评价指标作为评判依据。

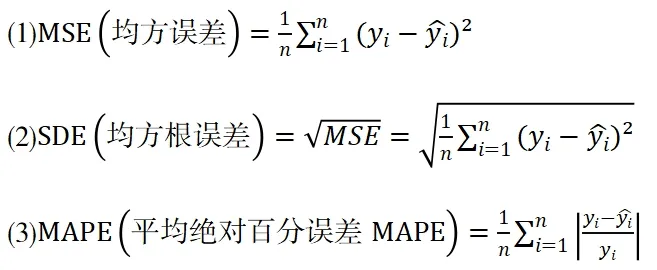
MSE、SDE、MAPE越小，则模型的预测精度越高。

2.苏州市城镇常住居民人均可支配收入预测

2.1 基于三次指数平滑法的预测

2.2 基于趋势外推法的预测

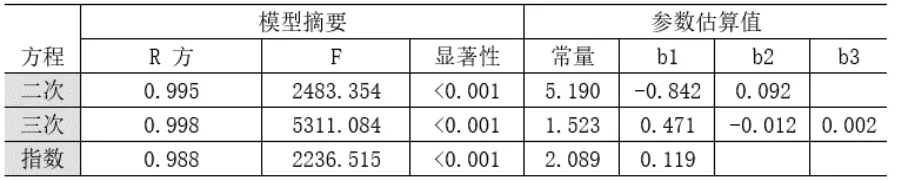
为确保预测模型的准确性，建立了不同的趋势模型，分别为二次模型、三次模型以及指数曲线模型，通过SPSS 26软件进行趋势拟合。

?

显著性水平均小于0.001，通过检验。三次模型拟合度R方为0.998，该模型拟合度最好，二次模型拟合度R方为0.995次之，拟合度最差的是指数模型，其R方为0.988。因而在运用趋势外推法时，建立苏州市城镇常住居民人均可支配收入的三次（抛物线）预测模型。

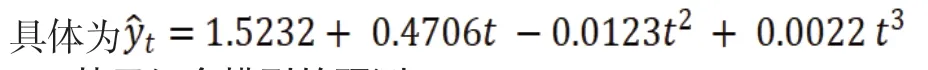
2.3 基于组合模型的预测

因此建立如下的预测模型：

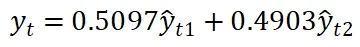
2.4 各模型预测精度评价

用上述三个模型分别对苏州市城镇常住居民人均可支配收入进行预测，并通过MSE、SDE、MAPE三项指标来评价预测精度（见表 3）

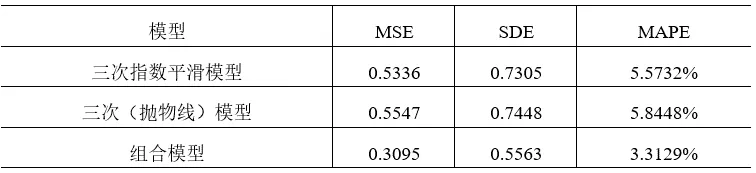
表2 各模型预测精度比较

可以明显的看出，组合模型(MSE，SDE，MAPE)<三次指数平滑模型 (MSE，SDE，MAPE)<三次（抛物线）模型(MSE，SDE，MAPE)，说明组合模型的预测精度高于其他单一模型，而三次指数平滑模型的预测精度又高于三次（抛物线）模型。

3.结论与局限

3.1 研究结论

本文以苏州市城镇常住居民人均可支配收入为例，除了建立单个预测模型外，，通过构建组合预测模型，综合了各个单项预测模型的优点，并与其他两个单一模型在MSE、SDE、MPAE三个指标上进行比较，发现组合模型的预测精度是最高的，因而选用组合预测模型作为苏州城镇常住居民人均可支配收入的预测工具，可以进一步推广到苏州以外城市的居民人均可支配收入的预测。

3.2 研究局限

本文选取的组合预测模型在各模型的权重计算过程中，采用的是方差倒数法，与其余两个预测模型的误差平方和密切相关，因而组合预测模型是在单一模型预测结果的基础上进行的，受单一模型选择是否合理的影响较大。

本文出现的三种预测模型均未对外部环境因素加以考虑，如在2020年，新冠疫情的出现可能会使本文模型的预测结果与苏州的实际情况有所出入。