基于混合迁移学习的运动想象分类算法研究及其在脑机接口中的应用
杜义浩,刘兆军,付子豪,张园园,任 娜,陈 杰,谢 平
(1. 燕山大学 河北省测试计量技术及仪器重点实验室,河北 秦皇岛 066004;2. 燕山大学 电气工程学院,河北 秦皇岛 066004;3. 燕山大学 体育学院,河北 秦皇岛 066004)
1 引 言
由于脑电信号具有非线性、非平稳性的特点,在使用前为保证系统识别准确率,脑机接口(brain-computer interface,BCI)系统[1~3]需进行长时间的训练过程来获取足够多的训练数据,这导致设备、时间成本高,使用便捷性差,限制了其实际应用。迁移学习可有效利用现有数据样本实现训练集的快速扩充,在保证识别准确率的同时提升系统使用便捷性,为解决BCI系统训练时间过长的问题提供了新的解决思路。
迁移学习主要包括3种迁移方式,实例迁移、特征迁移和模型迁移,其中实例迁移和特征迁移最为常用。为提升迁移学习的迁移效率,学者们进行了大量的探索研究。实例迁移学习方面,如,基于简单贝叶斯模型实现对源域样本的筛选,保证当前任务模型的训练效果,用于提升人脸识别的准确率[4];基于Logistic回归分析的直推式迁移学习,通过权重调整进行样本筛选,保证分类模型性能,用于文本分析[5];利用互近邻思想选择迁移对象,提升合并训练集的样本质量,用于解决数据流分类过程中样本标注和概念漂移问题[6]。这些研究着眼于实例层面,通过在源域样本集中选取与目标域样本分布最为相似的样本,实现训练集扩充目的。但源域与目标域中样本数据本身存在差异,经过实例迁移后仍无法消除。实例迁移仅适合两域样本差异较小的情况,使得其适用范围较为局限。特征迁移方面,如,通过最小化扩展非参数最大均值差异矩阵,拉近两域数据分布距离,实现多工况下湿式球磨机负荷参数测量[7];将最大均值差异距离度量准则应用于二分类运动想象,减少训练样本和测试样本的分布差异,以提高分类准确率[8];将基于最大方差展开的特征降维方法与最大均值差异相结合,实现源域与目标域分布距离的最小化,通过WIFI数据与文本数据进行方法的有效性验证[9]。上述研究着眼于特征层面,通过特征映射的方式寻找两域分布差异最小的希尔伯特空间,实现两域分布距离的拉近。但特征迁移忽略了样本本身是否适合迁移,若源域中存在大量的与目标域样本分布差异较大的样本,将会严重影响迁移效率。综上所述,现有迁移学习方法只考虑实例层面/特征层面的迁移效果,由于源域和目标域数据集本身的特性,使得基于单一模式的迁移学习可能存在迁移效果不明显甚至出现负迁移的情况。同时,迁移学习方法虽已广泛应用于人脸识别等等领域,但在运动想象BCI系统方面的应用较为少见,尤其是进行在线识别应用更少。
本研究构建了基于混合迁移学习的运动想象分类算法,结合实例迁移与特征迁移方法的各自优势,提升迁移效率与迁移方法的普遍适用性。首先,对运动想象数据进行预处理和特征提取;进而改进TrAdaBoost算法[10,11],从实例样本层面对源域样本进行筛选,提升训练集样本质量;最后基于大间隔投射迁移支持向量机[12,13],从特征层面实现两域分布距离最小化,进一步提升迁移效率。进一步,基于BCI 2008竞赛Dataset IIb数据集[14]与运动想象在线识别系统的实测数据集验证了本方法的有效性、普适性与实用性。
2 运动想象脑电信号特征提取
针对运动想象脑电信号的非线性、非平稳特点,为全面表征脑电信号事件相关去同步(event related desynchronization,ERD)/事件相关同步(event related synchronization,ERS)现象[15,16],本研究从时域、频域和时频域进行特征分析,特征量包含Hjorth参数,最大熵功率谱参数及时频能量,以综合定量刻画脑电信号特性。
2.1基于Hjorth参数的时域特征提取
Hjorth参数[17,18]定义了活动性(activity,Act)、移动性(mobility,Mob)和复杂性(complexity,Com)3个时域参数,分别定量描述脑电信号的方差、平均频率和带宽。本研究选取参数Act和Mob作为特征量,以表征脑电信号的时域特征。参数的计算公式为:
(1)
式中:Var表示方差;y(t)为运动想象脑电信号。基于Act和Mob参数构建脑电信号时域特征FHjorth为:
(2)
式中C3、C4为与运动想象最相关的脑电通道。
2.2 基于最大熵功率谱估计的频域特征提取
最大熵功率谱估计(power spectral density,PSD)是一种基于AR模型的参数谱估计法[19~21],目的是提升频谱质量。最大熵功率谱为
(3)
式中:f为频率;ω为角频率;p为AR阶数;αk和σω为Yule-Walker方程的解。根据运动想象ERD/ERS信号频谱特点,选取8~30 Hz的最大熵功率谱作为特征:
FPSD=[C3PSDC4PSD]
(4)
2.3 基于时频能量的时频特征提取
经验模态分解(empirical mode decomposition,EMD)[22~24]将信号分解为多个固有模态函数(intr-insic mode functions,IMFs),并经希尔伯特变换得到希尔伯特频谱,以用于定量表征脑电信号的时频域特征。EMD的表达式为:
(5)
式中:S(t)为原始信号;Ci(t)为第i个IMF分量。Rn(t)为剩余的部分。
对每一个IMF分量进行希尔伯特变换:
(6)
分解信号为:
Xi(t)=Ci(t)+jY(t)=Ai(t)ejθi(t)
(7)
然后计算瞬时振幅Ai(t)和瞬时相位θi(t)。
(8)
(9)
瞬时频率为:
(10)
故希尔伯特谱为:
(11)
瞬时能量谱(instantaneous energy spectrum,IES)代表在不同时段的能量分布[25],本研究将IES作为特征量:
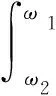
(12)
由于mu节律和beta节律是运动想象过程中最显著的频段,选取ωmu1(8 Hz)和ωmu2(13 Hz)、ωbeta1(14 Hz)和ωbeta2(30 Hz),得到IESmu和IESbeta。
故能量特征为
(13)
得到运动想象脑电特征矩阵:
F=[FHjorthFPSDFenergy]
(14)
3 基于混合迁移学习的运动想象分类算法
迁移学习的目的在于提升数据样本复用性,快速扩充训练集,若应用于BCI系统可有效提升其使用效率。本研究针对现有方法存在的问题,为增强迁移效率与迁移方法的普适性,基于第2节提取的特征集,构建了混合迁移学习运动想象分类模型。
3.1 混合迁移学习模型可行性分析
实例迁移从样本层面,通过样本加权提升源域样本质量,特征迁移从特征层面,通过特征重映射拉近两域的分布距离。本研究结合实例迁移和特征迁移构建了混合迁移学习模型,以提升迁移效率及方法普适性。实例迁移、特征迁移和混合迁移学习模型的理想迁移效果见图1所示。

图1 实例迁移、特征迁移和混合迁移学习模型迁移效果示意图Fig.1 Schematic diagram of transfer effects of instance transfer,feature transfer and hybrid transfer learning model
由图1(a)可见,由于源域和目标域样本存在分布差异,使得两域自训练得到的分类边界在空间上具有明显的差异,若用源域模型对目标域样本进行分类识别,分类误差较大;由图1(b)可见,实例迁移以目标域的样本分布为标准,经过多次迭代过程移除源域中与目标域样本分布差异较大的样本,可以有效降低两域的横向误差;由图1(c)可见,特征迁移目标是寻找最优特征映射矩阵,实现在某维度希尔伯特空间中两域分布距离最小化,可以有效降低两域的纵向误差;图1(d)为混合迁移效果,首先基于实例迁移完成样本筛选,可提升训练样本集的质量,进而在优化的训练集基础上进行特征迁移,通过特征重映射寻找两域分布差异最小的希尔伯特空间。通过对比各图可以发现,经混合迁移学习后可使两域分布距离最小,迁移学习效果达到最优。
3.2实例迁移—改进的TrAdaBoost算法
TrAdaBoost算法[10,26]属于直推式迁移学习算法,利用少量目标域样本和大量源域样本以迭代与样本加权的方式优化源域训练样本集质量,进而得到性能良好的分类模型。
具体来说,定义合并的训练样本集为:
D={Ds,Dt}={xi,yi}
(15)
式中Ds为源域训练样本集;Dt为目标域训练样本集;xi为样本实例;yi为标签。
(16)
定义测试样本集:
(17)
为合并的训练样本集中每个样本赋予初始权重:
(18)
并设置调整因子:
(19)
其中N为迭代次数,则第t次迭代过程中训练样本的权重分布为:
(20)
利用支持向量机(support vector machine,SVM)[11]获取分类模型,并对合并的训练样本集进行标签预测,利用Hedge(β)算法和AdaBoost算法对误分源域样本与误分目标域样本的权重进行上升与下降调整
(21)
经过N次迭代过程,即可得到在合并训练集上新的权重分布PN。
为降低计算成本并便于将优化的训练样本集作为特征迁移算法的输入,于是本研究依据样本极化原理对上述TrAdaBoost算法进行了改进,即样本的初始权重为

(22)
利用SVM获取分类模型,对样本集D进行标签预测,并根据分类结果对训练样本权重进行如下调整。
(23)
经过N次迭代过程,得到新的合并训练集:
(24)
经过改进的TrAdaBoost算法完成对源域训练样本的筛选,提升了合并训练样本集质量,完成训练样本集优化过程.
3.3 特征迁移——大间隔投射迁移支持向量机
在实例迁移优化后的训练集基础上,本研究引入大间隔投射迁移支持向量机[12,13,27]实现源域与目标域分布距离的进一步拉近。该算法基于最大均值差异(maximum mean discrepancy,MMD)的思想,通过重映射将特征矩阵映射至高维希尔伯特空间中,实现源域与目标域分布距离的拉近。
对于特征数据集Ds={x1,x2,x3,…,xn}和Dt={z1,z2,z3,…,zm},其MMD距离为:
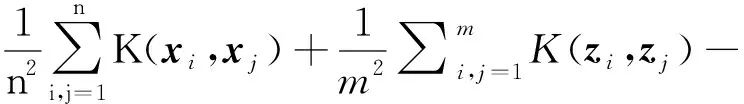
(25)
式中φ(·):X→H为映射函数;K(·)为核函数。
将MMD与SVM相结合,要求在保证对训练集分类性能的同时实现两域分布距离的最小化。因此,基于MMD的迁移支持向量机可以表示为:
(26)
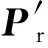
(27)
则优化目标最终定义为:

(28)
式中映射向量w为线性决策函数的方向向量,是被核函数K定义在希尔伯特空间中的向量。由表征定理可知,任何可使上式最小化的映射向量w必须是源域与目标域样本的核特征向量的线性组合。
(29)
设
φ(S)=(φ(S1),φ(S2),…φ(Sn+m))=
(φ(x1),φ(x2),…φ(xn),φ(z1),
φ(z2),…φ(zn))
(30)
式中φ(S)为训练数据和测试数据的核特征向量集。将式(28)代入式(30)中,则2个数据集的投影分布距离可以表示为:
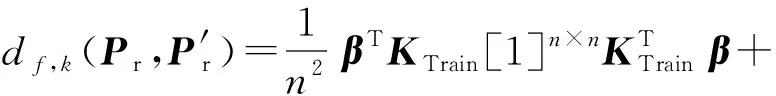
(31)
式中:KTrain为源域数据的(n+m)×n阶核矩阵;KTest为目标域数据的(n+m)×m阶核矩阵;Ω为(n+m)×(n+m)阶对称半正定矩阵。大间隔投射迁移支持向量机的优化目标最终可表示为:
yi(βTKj+b)≥1-εj; ∀j=1,2,…,n
(32)
综上所述,在实例迁移后的优化训练集基础上通过特征集重映射,实现特征集分布距离最小化,完成特征迁移过程。
3.4 混合迁移学习模型
根据上文中关于实例迁移和特征迁移的描述,本研究构建的基于混合迁移学习的运动想象分类模型的整体流程如图2所示。
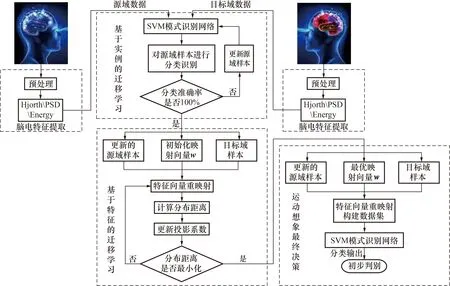
图2 基于混合迁移学习的运动想象分类模型流程Fig.2 The flowchart of motion imagery classification model based on hybrid transfer learning
首先对样本进行预处理,并利用第2节中的方法进行特征提取;根据2.2节中的实例迁移学习算法,将来自不同被试的特征数据集作为改进的TrAda-Boost算法的输入,利用SVM进行模式识别,以迭代方式筛选源域样本,提升训练集样本质量;根据2.3中的特征迁移算法,将优化的源域、目标域训练样本集和初始化映射向量w作为输入,基于MMD理论对投影系数进行最优查询,实现两域分布距离的最小化;最后构建最优分类模型,进行运动想象实验分类。
4 实验验证与结果分析
4.1 数据库仿真分析
为了验证本方法的有效性,基于BCI 2008竞赛Dataset IIb数据集[16]进行实验验证。本研究随机选取了5名被试者的数据,采样通道为C3、Cz、C4,每名被试样本总量为160,分别作为训练样本集和测试样本集,数据信息如表1所示。
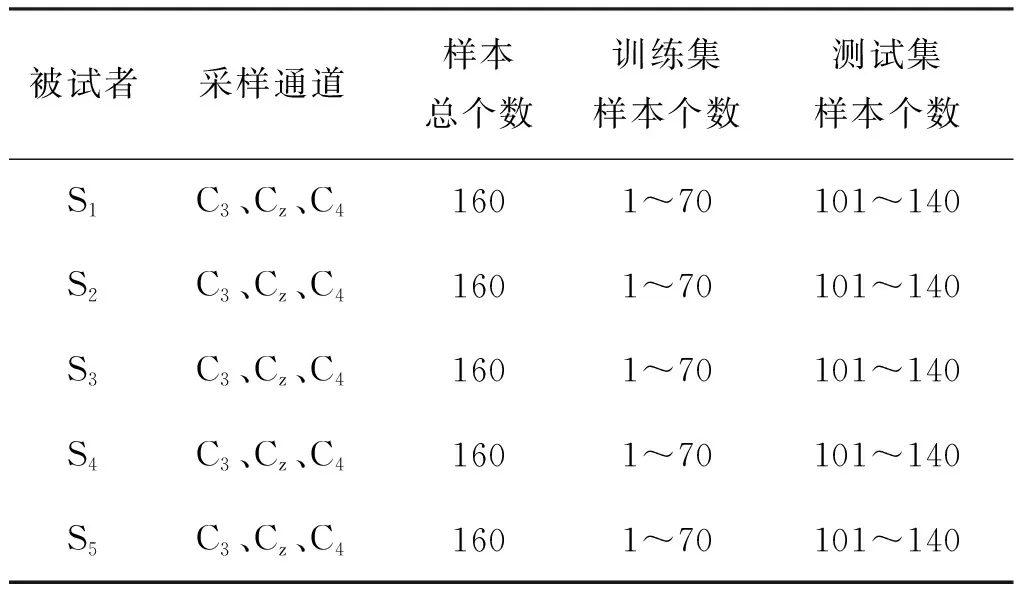
表1 BCI 2008竞赛Dataset IIb信息Tab.1 Dataset IIb properties
采用4阶巴特沃斯滤波器对原始信号进行8~30 Hz带通滤波,设置阻带截止频率分别为6 Hz和32 Hz,获取mu节律和beta节律频段,并进行 250 Hz 至200 Hz的降采样。
分别计算被试S1~S5运动想象脑电信号的时域、频域和时频域特征指标值。图3为单特征指标均值。由图3(a)可见,在被试者进行左手运动想象过程中,C3通道的mu节律的Act参数要明显高于C4通道的mu节律;相反地,由图3(b)可见,在被试者进行右手运行想象过程中,C3通道的mu节律的Act参数要明显低于C4通道的mu节律;由图3(c)可见,在被试者进行左手运动想象过程中,C3通道的beta节律的Act参数要明显高于C4通道的beta节律;相反地,由图3(d)可见,在被试者进行右手运行想象过程中,C3通道的beta节律的Act参数要明显低于C4通道的beta节律。同样的,被试者进行左右手运动想象过程中的Mob参数和时频能量特征具有与Act参数相似的变化规律。被试者进行左右手运动想象实验时,其mu节律和beta节律对应频段具有更高的PSD。由图3(e)可见,在进行左手运动想象实验时,C3通道的PSD整体高于C4通道。由图3(f)可见,在进行右手运动想象实验时,C3通道的PSD整体低于C4通道。
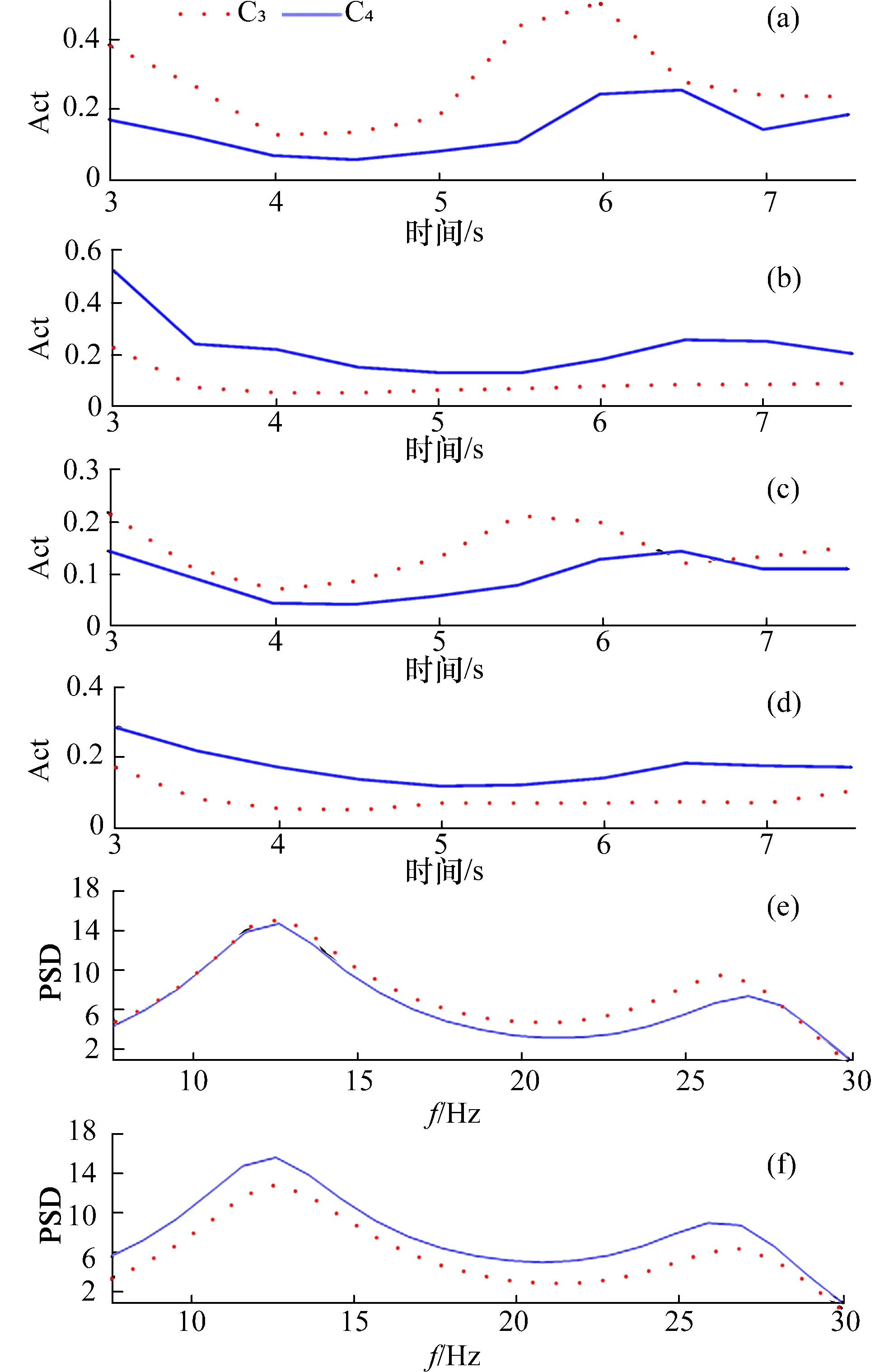
图3 运动想象脑电信号特征Fig.3 Motor imagery EEG signal features
将选取的被试数据集视为5个差异分布的数据集,对特征矩阵进行归一化处理后,分别利用SVM方法、实例迁移、特征迁移以及混合迁移学习模型进行测试。对于单特征与多特征,测试结果如图4所示。

图4 单特征与多特征迁移效果对比Fig.4 Comparison of single feature and multi-feature transfer performance
由图4可见,首先,多特征混合迁移识别准确率均值为78.48%,对于单特征的时域混合迁移、频域混合迁移和时频域混合迁移,识别准确率分别为69.0%、=67.2%和74.5%,显然,多特征混合迁移效果要优于单特征混合迁移效果,并且时频域混合迁移效果要优于时域混合迁移和频域混合迁移;其次,对于任一特征集合,混合迁移学习模型对迁移效率的提升均明显高于实例迁移与特征迁移。
由分析可知,将多特征矩阵作为分类学习模型的输入,能在有效提升迁移效率的同时提升迁移学习模型分类识别准确率,对于BCI 2008竞赛Dataset IIb数据集,测试结果如表2所示。
由表2可见:1)训练样本来自于目标域,即训练样本与测试样本满足独立同分布条件,模型识别准确率为79.4%~87.5%,识别精度最高,说明此时得到的分类器性能最佳;2)训练样本来自于源域,模型识别准确率均值仅为65.68%,说明此时得到的分类器性能最差;3)训练样本来自于源域,经过实例迁移、特征迁移、混合迁移学习模型分类,其识别准确率均值由65.68%分别提升至72.44%、73.64%、78.48%,且3种迁移方式的识别准确率相对提升均值分别为38.4%、47.1%、74.0%,说明混合迁移学习模型对迁移效率有明显的提升效果;4)训练样本来自于源域,实例迁移、特征迁移、混合迁移三种迁移学习方式的识别准确率相对提升标准差分别为0.19、0.23、0.12,说明混合迁移学习模型对于不同的迁移对象普适性更强。

表2 5名被试数据测试对比Tab.2 Comparison of 5 subjects (%)
因此,基于BCI 2008竞赛Dataset IIb数据集进行离线分析,验证了混合迁移学习模型不仅能大幅度提升迁移效率,同时也增强了迁移方法的普遍适用性。
4.2 运动想象在线实验分析
为进一步验证本方法在BCI系统实际应用中的实用性,基于如图4所示运动想象在线识别系统,选取20名(15男5女,年龄24±2岁)被试者参与本次实验,实验开始前,要求被试者睡眠充足,24 h内没有饮酒、喝茶等,依据系统界面的动画和语音提示进行70次训练。具体训练过程如图5所示,实验开始时,屏幕中央出现小实心圆和不断缩小的空心圆提醒被试者集中精神即将开始训练,此过程持续 2 s;第2 s后空心圆消失,实心圆随机向右或向左移动,被试者跟随实心圆移动方向进行右手或左手抓握运动想象;第6 s后实心圆消失,提示被试者想象过程结束,之后有4 s时间供被试者休息,并准备下一次运动想象过程。选用Neuracle脑电采集设备采集被试者脑电信号,电极按照10~20国际标准放置,具体采集C3、Cz、C4通道。

图5 运动想象在线实验Fig.5 Motion imaging online experiment

图6 单次运动想象实验范式Fig.6 Single motion imagery experiment paradigm
在20名被试者中随机选取5名(S6~S10),对实测数据进行1 000 Hz至200 Hz降采样,并采用与3.1节中同样的模式进行测试分析,结果如表3所示。
由表3可见,运动想象在线实验测试结果表现出与BCI数据集离线测试结果相似的变化规律,经实例迁移、特征迁移、混合迁移学习模型分类,其识别准确率相对提升均值分别为43.6%、49.1%、77.1%,同时其识别准确率相对提升标准差分别为0.21、0.19、0.09,说明混合迁移学习模型迁移效率最高、普适性更强,也同样证明了其在BCI系统实际应用中的实用性。

表3 5名被试数据测试对比Tab.3 Comparison of 5 subjects (%)
5 结 论
本研究构建了一种基于混合迁移学习的运动想象分类模型。首先依据样本权重极化原理改进TrAdaBoost算法,完成训练样本集优化;进而在优化的训练集基础上引入大间隔投射迁移支持向量机完成特征迁移过程,实现迁移效率与方法普适性的进一步提升。将本研究应用于BCI竞赛Dataset IIb数据集,并与SVM、实例迁移、特征迁移3种方法横向对比分析,由实验结果可知,本研究构建的混合迁移学习模型迁移效果提升明显,并且其对于不同的迁移对象的普适性更强。此外,基于运动想象在线识别系统进行在线测试,得到与离线数据相似的实验结果,证明了混合迁移学习模型的有效性与普适性,同时提高了运动想象BCI系统的实用性,为BCI系统的广泛应用奠定了基础。

