基于最大相关熵准则的多尺度高斯核极端学习机

刘兆伦，武 尤，王卫涛，张春兰，刘 彬

(1.燕山大学 河北省特种光纤与光纤传感重点实验室，河北 秦皇岛 066004；2.燕山大学 信息科学与工程学院，河北 秦皇岛 066004；3.燕山大学 电气工程学院，河北 秦皇岛 066004)

1 引 言

针对传统前馈神经网络学习速度慢的问题，黄广斌等人提出了极端学习机(extreme learning machine，ELM)[1]，但通过人为试凑法设定的隐含层节点个数以及隐含层激活函数的选择对ELM的学习效率和鲁棒性有很大的影响[2]。针对这些问题，有学者利用Mercer理论将具有良好的非线性映射能力的核函数引入ELM中形成核ELM[3]，不但避免了隐含层节点个数的设定和隐含层激活函数的选择，又提高了ELM的非线性映射能力。不同核函数所具备的性能不同，因此对于不同的特点的数据，同一个核函数的表现差异较大，单个核函数对输入数据进行映射的处理将不再合理。针对这个问题，学者们开始对多核ELM进行研究[4,5]。

随着多尺度分析和小波理论的发展，多尺度核学习作为多核学习的一种特殊形式[6]，因与合成核相比更具泛化能力和灵活性而被广泛应用。Liu等人将多尺度核ELM应用于脑电图信号(EEG)特征分类问题[6]；Chang等人利用多尺度核ELM解决相对磁导率曲线的计算问题[7]；王新迎等人将多尺度核ELM用于对多元混沌时间序列的建模预测[8]；Chen等人利用多尺度核ELM对电路系统输电线路进行故障诊断[9]。但是以上文献中现有的核函数多尺度化方法存在着计算复杂的问题，且大量的计算使得网络学习时间变长。

现有的多尺度核ELM均是采用最小二乘法的思想，基于最小均方差(minimum mean square error，MMSE)准则构建的[10]，对粗差数据十分敏感且往往存在过拟合的现象，在难免存在噪声的实际应用过程中，逐渐显示出其弊端。而近年来，作为一种新的随机变量局部相似性的度量，相关熵受到广泛关注[11,12]。最大相关熵准则(maximum correntropy criterion，MCC)从M-estimate框架来看，等价于加权最小二乘法[13]，相比于MMSE准则具备更优的抑制噪声的作用和更好的鲁棒性[14]，能有效地处理噪声数据。张金凤等人采用MCC准则对投影近似子空间跟踪算法的目标函数进行修正，推导出适用于噪声环境的新算法[15]；Wang等人利用MCC准则抑制混沌时间序列预测中脉冲噪声干扰的影响[16]；Wang等人将MCC准则引入核回归中提出了一种基于MCC准则的核回归脉冲星轮廓去噪方法[17]；Su等人用MCC准则代替基于高斯混合模型的图像恢复方法中的MMSE准则，避免了MMSE准则对异常值敏感的问题[18]。

针对上述多尺度核ELM现存的问题，本文采用MCC准则代替传统的多尺度核ELM算法中的MMSE准则构建目标函数使之适用于高斯噪声环境，并且基于按训练样本数量随机生成尺度因子的新型多尺度化方法，采用拉格朗日乘子法推导出基于MCC准则的多尺度核ELM算法(MCC-MKELM)，并对其进行收敛性与计算复杂度分析。针对3种对比算法在基准回归数据集与高斯噪声数据集上进行对比实验来验证其性能。最后将其应用于对水泥熟料f-CaO含量的预测以评估其实用性。

2 基于最大相关熵准则的多尺度高斯核极端学习机

2.1 最大相关熵准则

相关熵是一种用来衡量特征向量之间相似性的相关函数，对于任意给定的2个变量A、B可以定义为：

V(A,B)=E[k(A,B)]

(1)

式中：E(·)表示对两个变量A、B之差进行高斯变换后的函数期望[15]；k(·)为满足Mercer条件的高斯核函数[16]。但在实际问题中，变量A、B的联合概率密度往往未知，因此式(1)中的期望用训练样本估计量近似表示，设样本总数为S，ai、bi表示第i个样本在矩阵A、B中对应的元素，同时代入高斯核函数并用σ表示尺度因子，得到最大相关熵(MCC)准则表达式为：

(2)

2.2 基于最大相关熵准则的核极端学习机

使用MCC准则代替ELM中的MMSE准则并加入正则化项，得到求解ELM输出权重矩阵的新目标函数：

(3)

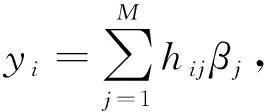
针对此非线性优化问题，半二次优化技术利用训练样本对输出权重进行迭代寻优得到的结果可能并不是最优解，因此本文使用拉格朗日乘子法进行求解。

目标函数：

约束条件：

εi=ti-yi=ti-hiβ(i=1,…,S)

(4)

式中:hi表示第 个训练样本经过ELM隐含层映射得到的特征向量；εi为第i组训练样本的训练误差。

运用式(4)构造拉格朗日函数：

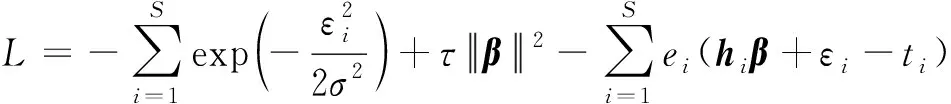
(5)

式中ei表示第i个训练样本对应的拉格朗日乘积因子。对式(5)进行求导得到：

(6a)

(6b)

(6c)

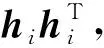
(7)

将变换后的求导结果进一步写成矩阵形式为：

(8)

式中:H表示全部训练样本通过ELM隐含层映射得到的特征矩阵；E表示由S个训练样本对应的ei所构成的向量。由式(8)求得输出权重β的表达式：

(9)

则最终网络输出可表示为：

(j=1,…,N)

(10)

式中：f(xj)表示第j个测试数据的预测输出；N为测试样本数目；h(xj)表示第j个测试数据的隐含层输出矩阵,h(xj)=[h1j,h2j,h3j,…,hMj]。用核函数取代式(10)中的内积计算便可得到基于MCC准则的核极端学习机为：

(11)

(12)

2.3 基于最大相关熵的多尺度高斯核极端学习机

高斯核函数是典型的可多尺度化核函数，传统的多尺度高斯核有两种形式: 一种是多尺度合成核[6]，如式(13)所示，不同尺度的核函数相加合成一个核; 另一种是大小尺度叠加核[4]，如式(14)所示，先用大尺度核处理平缓变化的数据，再用小尺度核处理剧烈变化的样本，最后使多个尺度得到的结果相加。用R表示尺度个数。

(13)

f(x)=f(k1)+f(k2)+…+f(kR)

(14)

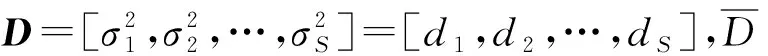
(15)

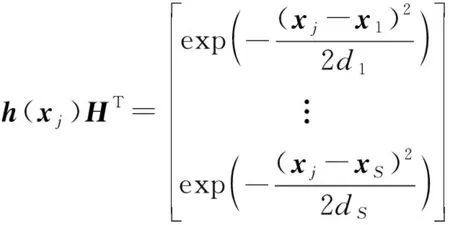
(16)

由此，得到一种基于最大相关熵准则的新型多尺度核ELM：

(17)

3 算法收敛性与复杂度分析

3.1 收敛性分析

在文献[1]中，Huang G B从非线性逼近能力和统计学习理论方面给出了ELM算法收敛的理论依据。本文提出的MCC-MKELM算法在基本ELM的基础上引入的多尺度核只是改变了计算方式，且每个核都是单一尺度的高斯函数，满足ELM的收敛条件，对ELM的收敛性并无影响。此外由拉格朗日乘子法理论可知，只有在目标函数是凸函数的情况下，才能保证求解得到的结果为所求解问题的最优解。本文引入的相关熵准则，使用高斯核函数保证了目标函数是凸的，从而确保了全局收敛，因此MCC-MKELM算法是收敛的。同时，MCC-MKELM算法保持了ELM的一次性学习特性，随机产生输入权重和隐含层阈值后不再需要迭代优化，因此MCC-MKELM算法也具有良好的收敛速度。

3.2 复杂度分析

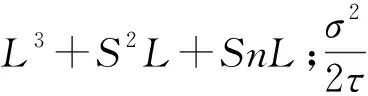
2L3+2S2L+SL(m+n)+1

(18)

对于采用式(13)所示多尺度化形式的，基于MMSE准则的多尺度核ELM，最终对应的计算复杂度为：

L3+2RS2L+RSL(m+n)

(19)

对于采用式(14)所示多尺度化形式的，基于MMSE准则的多尺度核ELM，最终对应的计算复杂度为：

R[L3+2S2L+SL(m+n)]

(20)

比较式(18)、式(19)与式(20)可以看出，本文提出的MCC-MKELM算法与传统多尺度核ELM算法相比，避免了尺度个数对计算复杂度的影响。在新多尺度化方法中R=S=L，使3种多尺度核ELM的隐含层神经元个数一致，则2种传统多尺度核ELM的计算复杂度明显大于MCC-MKELM算法。

4 性能验证

将MCC-MKELM算法与2种传统的ELM算法以及1种实验对比ELM算法在3种UCI基准数据集上进行性能对比，4种ELM算法如表1所示。其中算法2是为了验证MCC准则与MMSE准则的抗噪性能差异而设置的算法，只将算法1中的MCC准则替换为MMSE准则，而其他方面均保持不变，并没有文献出处。仿真实验均是基于Intel(R)Core(TM)i3-4150处理器、3.50 GHz CPU主频、4.00 GB内存和Windows7 32位操作系统的计算机，使用Matlab R2007b仿真软件进行的。

表1 4种ELM算法Tab.1 Four ELM algorithms

在数据集模型训练过程中，本文采用Hold-out方法，随机将各数据集的3/4作为训练数据，1/4作为测试数据。每组实验均重复运行50次，并将4种ELM在每组数据集上运行的时间平均值、测试样本数据的均方差平均值以及相关熵平均值进行统计。

4.1 对预测精度与学习速度的验证

为了全面地验证4种算法的性能，选取不同数量不同维度的3个典型的基准数据集进行性能验证，3个数据集均来自UCI机器学习数据库[19]，分别为：MachineCPU、AutoMPG、BostonHousing。算法1中τ=0.5，3个基准数据集上尺度因子随机生成的范围依次是：[0,0.001]、[0,0.015]、[0,0.035]。算法2中的所有参数包括尺度因子均与算法1保持一致。算法3中隐含层激活函数采用sigmoid函数，最大迭代次数设置为k=2 000。算法3与算法4中的正则化因子设置为C=20。算法4中的传统多尺度化方法采用应用更普遍且更具鲁棒性的式(14)的形式。仿真结果如图1～图3所示。

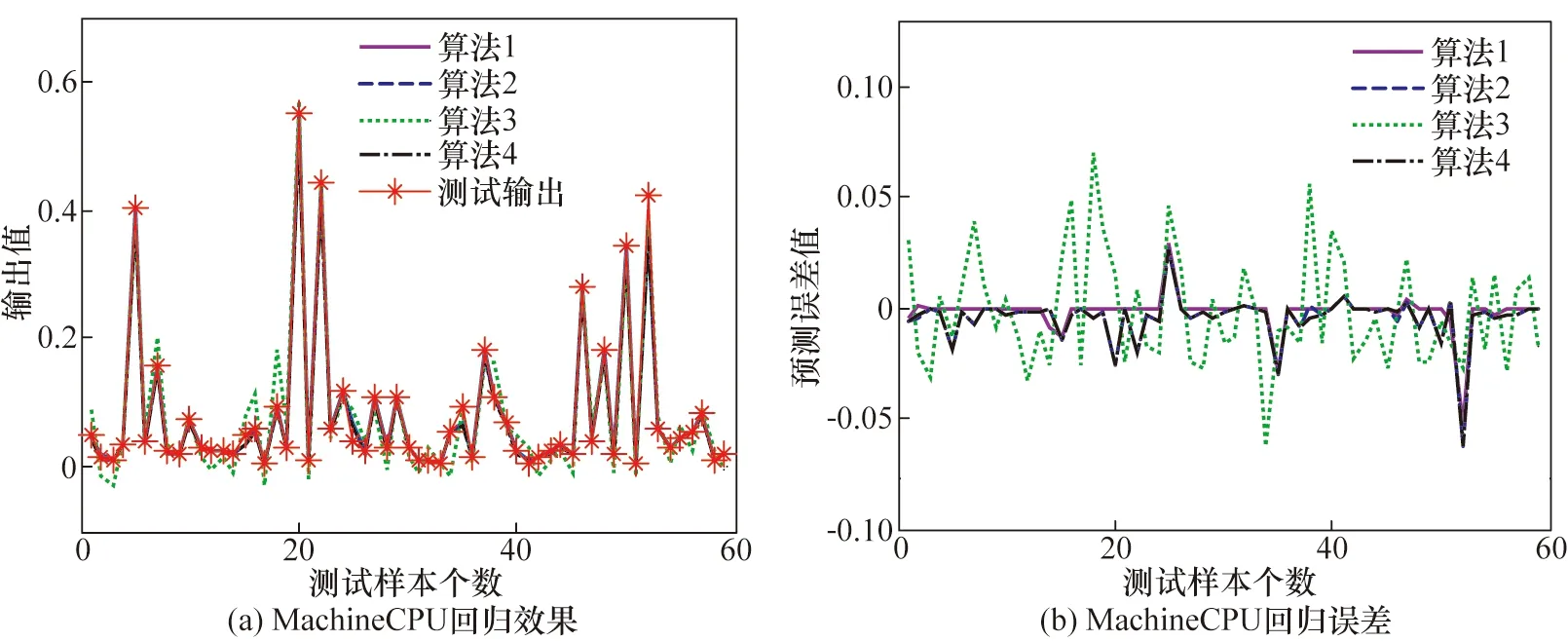
图1 4种ELM在MachineCPU数据集上的回归效果对比Fig.1 Comparison of the regression effects of four ELMs on the MachineCPU dataset

图1～图3分别为4种ELM算法在MachineCPU、AutoMPG和BostonHousing数据集上的回归效果对比图。以图2中AutoMPG数据集上的回归结果为例：图2(a)显示出算法3的回归效果相对最差，图2(b)可以更加直观地显示出算法1的回归误差曲线最稳定地贴近于0值且波动最弱，其次为算法2，最次为算法4。在其他2个数据集上，4种算法的对比结果与在AutoMPG数据集上基本一致。具体预测性能数据如表2所示。

图2 4种ELM在AutoMPG数据集上的回归效果对比Fig.2 Comparison of regression effects of four ELMs on AutoMPG datasets

表2 4种算法在UCI回归数据集上的性能统计Tab.2 Performance statistics of four algorithms on UCI regression dataset

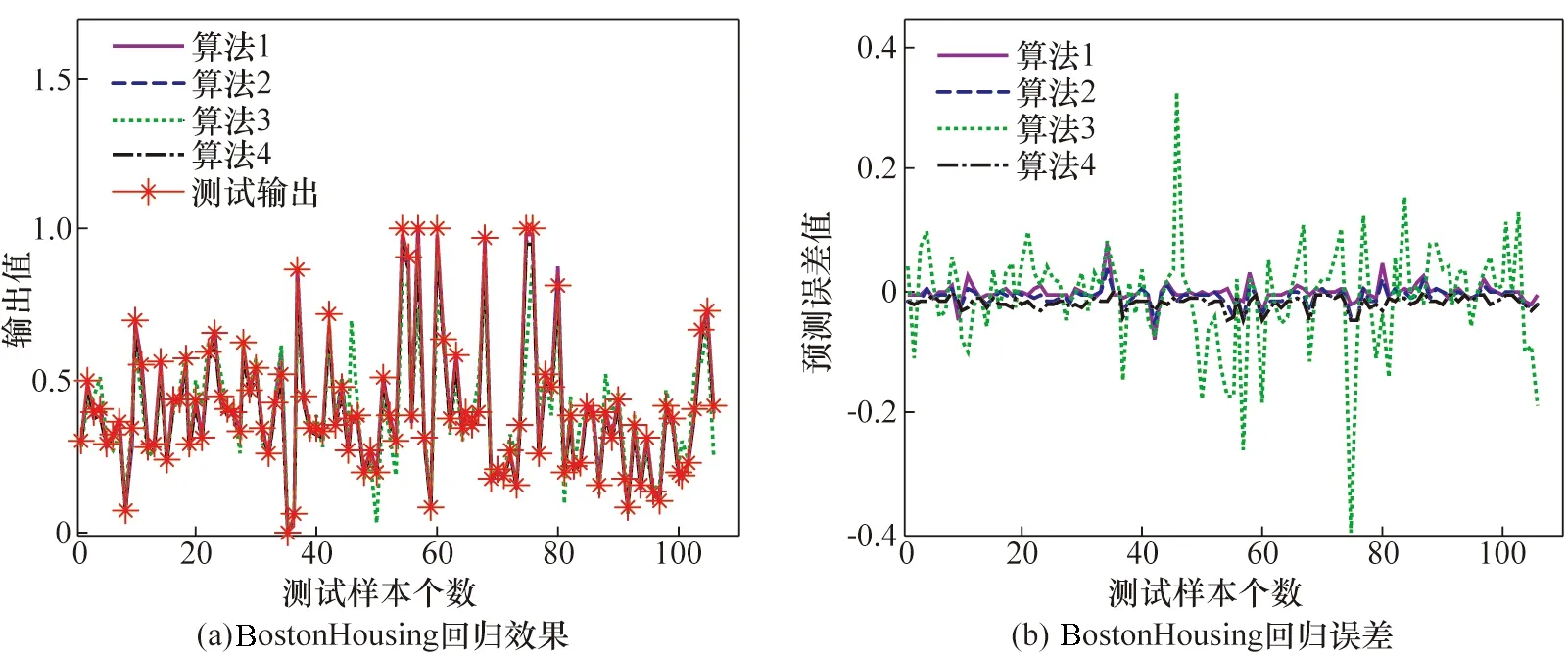
图3 4种ELM在BostonHousing数据集上的回归效果对比Fig.3 Comparison of regression effects of four ELMs on the BostonHousing dataset

从预测精度来看，仍以AutoMPG数据集为例：算法1均方根误差值为0.009 8，将预测精度较算法2提高9.26%，较算法3提高67%，较算法4提高30.98%。其中，算法1的预测精度明显优于算法3是由于:针对基于MCC准则对非线性优化问题的求解，相比于现有的半二次优化技术，拉格朗日乘子法可以得到更准确的最优值。算法1使用的多尺度高斯核与算法4使用的多尺度小波核相比，高维特征空间的维度更高，因此区分数据差异的能力也优于算法4。算法2与算法1除了构造目标函数依据的准则不同之外，两者的核函数、多尺度化方法、非线性问题的求解方法均相同，因此两者预测性能差别不大。

从3个数据集来看，算法2、算法3、算法4均存在均方差值随数据集数据量的增加而逐渐增大的趋势，而算法1在三个不同类型的数据集上的均方差数值依次为：0.010 1、0.009 8、0.011 4，可见算法1的泛化性能优于其他对比算法。同时，相比于传统多尺度核极端学习机的算法4，算法1在3个基准数据集上将预测精度平均提升30.30%。

针对学习速度而言，算法1的学习时间在3个基准数据集上均优于算法3与算法4。这是由于，算法2与算法4相比，在同样采用MMSE准则的前提下，采用新多尺度化方法，在不影响预测精度的情况下大大缩短了多尺度核的学习时间，明显提高了学习速度。而算法1不但采用了与算法2相同的多尺度化方法，还使用拉格朗日乘子法求解非线性问题避免了算法3中耗时的迭代过程。同样，由于算法1与算法2的核函数、多尺度化方法、非线性问题的求解方法均相同，因此两者的学习速度也相当。所以，整体来说算法1的学习速度是可取的。

4.2 抗噪性能验证

在第4.1节的实验中，算法1与算法2在基准数据集上都具有良好的预测精度和较优的学习速度。由于实际获取的数据往往含有噪声，因此在噪声数据集上对2种准则下的多尺度高斯核ELM进行实验。

图4 两种准则下的多尺度核ELM抗噪性能对比Fig.4 Comparison of multi-scale nuclear ELM anti-noise performance under two criteria

图4是在4种不同信噪比的高斯噪声环境下，采用MMSE准则的算法2与采用MCC准则的算法1的抗噪效果对比图。图4(a)显示在信噪比为25的高斯噪声下算法2与算法1相比回归精度稍差但差距不大；图4(b)显示在信噪比为20的高斯噪声下算法2开始出现轻微的过拟合现象，而算法1仍可以保持良好的回归精度；图4(c)显示在信噪比为15的高斯噪声下算法2的过拟合现象加剧，而算法1的回归精度略微下降但仍明显优于算法2；图4(d)显示在信噪比为10的高斯噪声下虽然两种算法的回归效果均变差，但是算法1仍能维持较好的sinc曲线形状且与算法2相比回归精度优势更加明显。

具体实验数据如表3所示。

表3 基于两准则下的多尺度核ELM在高斯噪声数据集上的性能统计Tab.3 Performance statistics of multi-scale kernel ELMbased on two criterias on Gaussian noise dataset

由实验数据分析得出：相比于算法2，在不同信噪比的高斯噪声环境中，算法1具有更强的抗高斯噪声的能力和鲁棒性。在信噪比为25的数据集上

将精度提高26.27%；在信噪比为20的数据集上将精度提高36.04%；在信噪比为15的数据集上将精度提高47.00%；在信噪比为10的数据集上将精度提高51.34%。实验数据验证了，使用MMSE准则的算法2在高斯噪声的环境下容易发生过拟合，而使用MCC准则在高斯噪声环境中的预测结果更可靠，特别是在信噪比小的环境中，本文所提出的算法1鲁棒性的优势更加明显。但本文所提出的算法1抑制高斯噪声的能力并非无限，随着信噪比的增强，精度相应变差。从学习速度来看，由于式(17)中存在2次求逆运算而使算法1的学习时间整体略高于算法2，但是权衡算法1在精度与鲁棒性上的提高，学习时间的牺牲是可以接受的，因此与算法2相比算法1具有更佳的性能。

5 应用案例

在水泥生产过程中，水泥熟料中游离氧化钙(free lime in cement clinker，f-CaO)含量是水泥熟料质量的一项重要指标，生产操作人员需及时掌握熟料f-CaO含量以调整生产操作[25,26]。

通过对水泥熟料生产工艺的分析，选取水泥熟料f-CaO含量预测算法的相关输入变量为：烟室氮氧化物含量(×10-6)、分解炉出口温度(℃)、二次风温度(℃)、烟室氧气含量(%)、烟室温度(℃)以及窑主机电流(A)，输出变量为水泥熟料f-CaO含量(%)[27]。

本文的实际数据来自某水泥厂生产线DCS系统和水泥熟料f-CaO含量化验室的历史记录，在最终获得的245组实验样中采用随机子抽样验证的方法，随机选取155组样本数据作为训练数据，剩余的90组数据作为训练验证数据。与第3节性能验证部分相同，采用计算时间、均方误差值、相关熵值作为水泥熟料f-CaO含量预测算法的性能评估指标，其他参数设置均与第4.1节中相同。实验仿真结果如图5所示。

图5 4种ELM的水泥熟料f-CaO含量预测效果对比Fig.5 Comparison of prediction effects of f-CaO content of cement clinker with four ELMs

图5显示了4种ELM算法应用于水泥熟料游离氧化钙含量预测的结果，可以看出算法1预测结果最贴近于对应的测试输出值，算法2与算法4次之，而算法3的预测结果与测试输出的拟合度最低。具体预测性能数据统计如表4。

表4 4种ELM对水泥熟料游离氧化钙含量的预测性能统计Tab.4 Predictive performance statistics of f-CaOcontent of cement clinker by four ELMs

由表4中的实验数据可以得出：由于算法1与算法2中既没有算法3中的迭代，也没有算法4中复杂的多尺度计算，算法1与算法2所需的运行时间明显少于算法3与算法4。4种ELM算法的预测均方差值分别为：0.009 9, 0.011 2, 0.030 6, 0.013 0。算法1的预测精度相对于算法2提高11.6%，相对于算法3提高67.6%，相对于算法4(传统多尺度核极端学习机)提高23.8%。综上所述，在4种ELM算法中算法1的预测精度最高且运算时间短，将其应用于水泥熟料游离氧化钙含量预测更具适用性和时效性。

6 结 论

本文构建了一种基于最大相关熵准则的多尺度高斯核极端学习机算法—MCC-MKELM。利用MCC准则建立目标函数，避免了多尺度核ELM中传统的MMSE准则对噪声敏感的问题，提高了多尺度核ELM在高斯噪声环境中的预测精度和鲁棒性。提出了一种新的针对核ELM的多尺度化方法，避免了传统多尺度化方法因计算量大而出现学习速度慢的现象，大大缩短了多尺度核ELM的学习时间。使用拉格朗日乘子法对非线性问题进行求解，避免了半二次优化技术中复杂的迭代，提高了求解输出层权值矩阵的速度和网络预测精度；同时保留了传统多尺度核ELM泛化能力强的优点并实现了对泛化性能的进一步优化。实验结果表明，本文提出的MCC-MKELM算法能快速准确地对水泥熟料f-CaO含量进行预测，为生产操作提供指导，具有重要的实际意义。

[参考文献]

[1] Huang G B, Zhu Q Y, Siwe C. Extreme learning machine: Theory and applications [J].Neurocomputing, 2006, 70(1): 489-501.

[2] Huang G B, Zhou H M, Ding X J,etal. Extreme learning machine for regression and multiclass classification [J].IEEETransactionsonSystems,Man,andCyberneticsPartB:Cybernetics, 2012, 42(2): 513- 529.

[3] 曾启明, 纪震, 李琰, 等, 基于ELM和MA的微型四频天线设计 [J]. 电子学报, 2014, 42(9): 1693-1698.

Zeng Q M, Ji Z, Li Y,etal. A Miniature Four-Band Antenna Design Using ELM and MA [J].ActaElectronicaSinica, 2014, 42(9): 1693-1698.

[4] 汪洪桥, 孙富春, 蔡艳宁, 等. 多核学习方法 [J]. 自动化学报，2010, 36(8): 1037-1050.

Wang H Q, Sun F C, Cai Y N,etal. On Multiple Kernel Learning Methods [J].ActaAutomaticaSinica, 2010, 36(8): 1037-1050.

[5] Liu X W, Wang L, Huang G B,etal. Multiple kernel extreme learning machine [J].Neurocomputing, 2015, 149(Part A): 253-264.

[6] Liu Q, Zhao X G, Hou Z G,etal. Multi-scale wavelet kernel extreme learning machine for EEG feature classification [C]// IEEE. IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems. 2015: 1546-1551.

[7] Chang P, Li S R, Ge Y L,etal. Computation of reservoir relative permeability curve based on multi-scale wavelet kernel extreme learning machine [C]// IEEE. Control Conference. 2016: 7179-7184.

[8] 王新迎, 韩敏. 多元混沌时间序列的多核极端学习机建模预测 [J]. 物理学报, 2015, 64(7): 129-135.

Wang Y X, Han M. Multivariate chaotic time series prediction using multiple kernel extreme learning machine[J].ActaPhysicaSinica, 2015, 64(7): 129-135.

[9] Chen Y Q, Fink O, Sansavini G. Combined Fault Location and Classification for Power Transmission Lines Fault Diagnosis with Integrated Feature Extraction [J].IEEETransac-tionsonIndustrialElectronics, 2018, 65(1): 561- 569.

[10] 牛培峰, 史春见, 刘楠, 等. 基于GSA-PELM的锅炉NOx预测模型 [J]. 计量学报, 2018, 39(5): 741-746.

Niu P F, Shi C J, Liu N,etal.Optimization for NOxPrediction Model from Boilers Based on GSA-PELM[J].ActaMetrologicaSinica, 2018, 39(5): 741-746.

[11] Santamaria I, Pokharel P P, Principe J C. Generalized correlation function: Definition, properties, and application to blind equalization [J].IEEETransactionsonSignalProcessing, 2006, 54(6): 2187-2197.

[12] Xing H J, Wang X M. Training extreme learning machine via regularized correntropy criterion[J].NeuralComput&Applic, 2013, 23(7-8): 1977-1986.

[13] 唐哲, 雷迎科. 基于最大相关熵的通信辐射源个体识别方法 [J]. 通信学报, 2016, 37(12): 171-175.

Tang Z, Lei Y K. Method of individual communication transmitter identification based on maximum correntropy [J].JournalonCommunications, 2016, 37(12): 171-175.

[14] Chen B D, Wang X, Lu N,etal. Mixture Correntropy for Robust Learning [J].PatternRecognition, 2018, 79: 318-327.

[15] 张金凤, 邱天爽, 李森. 冲激噪声环境下基于最大相关熵准则的韧性子空间跟踪新算法 [J]. 电子学报, 2015, 43(3): 483-488.

Zhang J F, Qiu T S, Li S,etalA Robust PAST Algorithm Based on Maximum Correntropy Criterion for Impulsive Noise Environments [J].ActaElectronicaSinica, 2015, 43(3): 483-488.

[16] 王世元, 史春芬, 钱国兵,等. 基于分数阶最大相关熵算法的混沌时间序列预测 [J]. 物理学报, 2018, 67(1): 283-290.

Wang S Y, Shi C F, Qian G B,etal. Prediction of chaotic time series based on the fractional-order maximum correntropy criterion algorithm [J].ActaPhysicaSinica, 2018, 67(1): 283-290.

[17] Wang Y D, Zheng W, Zhang D P,etal. Pulsar profile denoising using kernel regression based on maximum correntropy criterion [J].Optik-InternationalJournalforLightandElectronOptics, 2017, 130:757-764.

[18] Su Z M, Yang L, Zhu S M,etal. Gaussian mixture image restoration based on maximum correntropy criterion [J].ElectronicsLetters, 2017, 53(11): 715-716.

[19] Asuncion A, Newman D. UCI Machine learning repository [EB/OL]. (2018-09-24). http://archiveics.uci edu/ml/datasets.html.

[20] Chuang C C, Su S F, Jeng J T,etal. Robust support vector regression networks for function approximation with outliers [J].IEEETransactionsonNeuralNetworks, 2002, 13(6): 1322-1330.

[21] Abrarov S M, Quine B M. Sampling by incomplete cosine expansion of the sinc function: Application to the Voigt/complex error function [J].AppliedMathematics&Computation, 2015, 258(C): 425-435.

[22] Xu Y, Ye L L, Qun X Z. Improved dynamic recurrent-based ELM neural network for fault prediction [J].ControlandDecision, 2015,30(4): 623-629.

[23] Abrarov S M, Quine B M. Sampling by incomplete cosine expansion of the sinc function: Application to the Voigt/complex error function[J].AppliedMathematicsandComputation, 2015, 258: 425-435.

[24] 李凡军, 韩红桂, 乔俊飞. 基于灵敏度分析法的ELM剪枝算法 [J]. 控制与决策, 2014,(6): 1003-1008.

Li F J, Han H G, Qiao J F. Pruning algorithm for extreme learning machine based on sensitivity analysis [J].ControlandDecision, 2014,(6):1003-1008.

[25] 赵朋程, 刘彬, 孙超, 等. 基于IQPSO优化ELM的熟料质量指标软测量研究 [J]. 仪器仪表学报, 2016, 37(10): 2243-2250.

Zhao P C, Liu B, Sun C,etal.Soft sensor for cement clinker quality indicator based on IQPSO optimize ELM [J]ChineseJournalofScientificInstrument, 2016, 37(10): 2243-2250.

[26] 赵彦涛，何永强，贾利颖，等. 基于时间序列单维卷积神经网络的水泥熟料游离钙软测量方法[J]. 计量学报, 2020, 41(9): 1152-1162.

Zhao Y T, He Y Q, Jia L Y,etal.Soft Measurement Method for Cement Clinker f-CaO Based on Time Series Single-dimensional Convolutional Neural Network[J].ActaMetrologicaSinica, 2020, 41(9): 1152-1162.

[27] 刘彬, 赵朋程, 高伟, 等. 基于粒子群算法与连续型深度信念网络的水泥熟料游离氧化钙预测 [J]. 计量学报, 2018, 39(3): 420-424.

Liu B, Zhao P C, Gao W,etal.Prediction of Cement f-CaO Based on Particle Swarm Optimization and Continuous Deep Belief Network[J].ActaMetrologicaSinica, 2018, 39(3): 420-424.