交互式多模型集自适应协同滤波目标跟踪算法研究
孔德明,杨 丹,王书涛
(燕山大学 电气工程学院,河北 秦皇岛 066004)
1 引 言
为了准确地获得目标当前的位置和状态信息,高精度的跟踪技术变得越来越重要[1]。为了获得准确稳定的跟踪,必须有效地去除测量误差[2],精准获得目标运动状态估计参数,需要准确地对目标的运动状态进行估计[3],常见的模型有匀速运动模型(constant velocity,CV)、匀速度转弯运动模型(constant turn,CT)、匀加速度运动模型(constant acceleration,CA)、Singer模型[4]以及当前统计(current statistical,CS)模型。但是单一的运动模型在处理复杂的机动目标跟踪问题上容易出现较大的误差,甚至出现目标丢失的情况[5]。针对这个问题,Bar-Shalom提出了交互式多模型(interactive multiple model,IMM)算法[6],该算法引入了马尔科夫状态转移概率矩阵,使每个模型的输入状态都与一个动态模型相关联,并且使得这些所有的模型都相互作用,从各个模型的滤波器得出的状态估计通过加权得到最终状态估计。
IMM算法的出现使得目标跟踪不再是单一模型的匹配问题,传统交互式目标跟踪算法的模型采用的是固定结构固定参数,虽然能够克服单一模型对运动目标匹配误差大的缺点,但是模型集的固定使得在处理复杂场景的机动目标跟踪问题时只能通过增加模型个数来提高测量的精度。这将会导致该算法在一方面降低运算速度,在另一方面模型之间的竞争也会降低跟踪的精度的问题[7],并且模型参数的固定使得测量环境一旦发生较大的变化,模型将不再适合当前的测量情况,加大了估计误差。
对于固定结构参数IMM算法存在的问题,有关学者提出了许多有关跟踪准确性的算法。例如变结构多模型(variable structure multiple model,VSMM)算法[8],异构模型集协同滤波(novel interactive multiple model,Novel-IMM)算法以及混合目标跟踪算法[9]。在VSMM算法中采用的是自适应模型集,当机动目标的运动模式频繁发生切换时,模型集自适应匹配的不准确会导致目标跟踪精度下降的问题。Novel-IMM算法在面对机动目标运动模式时,不需要频繁地切换场景,具有较好的跟踪效果[10];但是实验表明当目标为CA或 CT状态时跟踪性能较好,当目标为CV状态时的跟踪效果较差,同时该算法相比较VSMM与固定结构交互多模型算法(fixed structure interacting multiple model,FSMM)算法在计算量方面也是成倍增加[11]。针对许多场景需要比较高的跟踪准确性,以上算法均难以达到要求。
本文提出了一种交互式多模型集自适应协同滤波(interacive multi-model set adaptive collaborative filtering,SAC-IMM)算法,SAC-IMM算法由3个拥有独立的模型集的滤波器组成,分别为CV-CT-CA-CV模型集、CV-CT-CA-CT模型集以及CV-CT-CA-CA模型集,3个模型集独立并行运行,并根据当前模型集中模型的概率和协方差进行模型集的自适应调整以达到更加准确跟踪的目的。
2 交互式多模型算法
在进行对目标的跟踪时,目标通常不是长期固定的处于同一运动状态,而是具有多种运动状态;所以当使用单个模型来进行对目标进行跟踪时,一旦目标发生机动变化,将会产生很大的跟踪误差甚至发生目标丢失的情况[12]。因此,在处理目标复杂的运动时通常会创建多个模型, IMM算法将系统视为有限状态下的马尔可夫链,并使用不同类型模型之间的转移概率进行交互[13]。考虑模型集中的单个模型为离散时间马尔可夫跳跃线性系统:
X(k)=F(k-1)X(k-1)+G(k-1)W(k-1)
(1)
Z(k)=H(k)X(k)+V(k)
(2)
式中:X(k)为k时刻的状态向量;Z(k)为k时刻的测量向量;F(k-1)、G(k-1)与H(k-1)分别为状态矩阵、输入矩阵和测量矩阵;与模型相关的过程噪声向量W(k)和测量噪声向量V(k)均为高斯白噪声,对应下文中的状态和测量噪声协方差矩阵Q(k)与R(k)。
IMM算法引入了马尔可夫状态转移矩阵[14],将模型集中的每个模型都参与到状态估计的运算中,目标状态的检测将由多个模型并行工作来完成,而不再是依靠单一模型,多模型的交互能够更加真实准确的描述机动目标的运动过程[15]。
本文实现的扩展卡尔曼滤波IMM算法的完整流程如下:
步骤1:计算各模型的初始混合概率
(3)
其中,
(4)

步骤2:计算混合状态输入估计
(5)
i,j∈S
(6)

步骤3:滤波
(a)状态一步预测
(7)
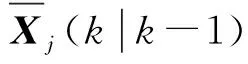
(b)进一步预测方差矩阵
Pj(k|k-1 )=Fj(k-1)P0j(k-1)Fj(k-1)T+
G(k-1)Qj(k-1)G(k-1)T
(8)
式中:Qj(k-1)表示k-1时刻的过程噪声协方差矩阵。
(c)计算滤波增益
Kj(k)=Pj(k|k-1)Hj(k)T·
[Hj(k)Pj(k|k-1)·Hj(k)T+Rj(k)]-1
(9)
式中:Hj(k)为k时刻第j个卡尔曼滤波器的测量矩阵;Rj(k)]为k时刻第j个滤波器的测量噪声协方差矩阵。
(d)状态估计量
新的状态估计是卡尔曼校正相应状态预测的结果,校正值由Kj(k)的值以及残差值δj(k)加权得到。
(10)
式中:残差值的公式为
(11)
(e)估计误差方差
Pj(k)=(I-Kj(k)Hj(k))Pj(k|k-1)
(12)
式中:I为单位矩阵。
步骤4:各模型可能的概率
得到模型的似然函数,计算每个模型在该模型集中所占的权重。
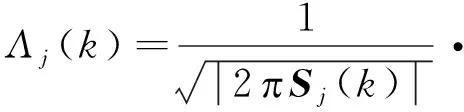
exp[-0.5·δj(k)T(Sj(k))-1δj(k)]
(13)
自相关矩阵Sj(k)为
Sj(k)=Hj(k)Pj(k|k-1)Hj(k)T+R(k)
(14)
式中:δj(k)表示k时刻模型j的信息(残差);Sj(k)表示k时刻模型j的信息协方差矩阵。
步骤5:各模型概率更新
(15)
式中:
(16)
步骤6:各部分信息融合
根据各模型概率更新的值,重新计算模型集中每个模型的状态估计值以及协方差矩阵。
(17)
(18)
3 SAC-IMM算法
为了实现在某些场景下精度需求较高的跟踪技术,本文提出的 SAC-IMM算法通过设立3个基于不同模型集的IMM滤波器,分别为CV-CA-CT-CV、CV-CA-CT-CA、CV-CA-CT-CT模型集。k-1时刻的模型概率信息将会作为k时刻的先验信息,分配概率最低的模型将会在k时刻的模型集中被删除,但同一模型集中只删除一个模型。这样在IMM1、IMM2和IMM3模型集中总存在CV-CA-CT(IMM0)模型集,当目标的机动状态发生改变需要剔除模型与激活新模型时,该模型将会在IMM0模型集中的作为概率最小或最大的模型输出。IMM1、IMM2和IMM3模型集恢复初始状态,继续重复上述过程,以达到模型集自适应的同时提高测量精度目的。
3个IMM滤波器协同工作并相互独立。利用模型集概率检测MSPT算法,从候选模型集中选择机动目标最优估计结果,提高跟踪精度。由于3个模型均初始化的前几个时刻先验信息与后验信息较少,故SAC-IMM算法的实现步骤分为前时刻a(0s~CHs)的状态估计与第k(k=CH+1,CH+2,…)步的状态估计。其中CH时刻为存在其中任意模型集中模型概率超过0.75的时刻;其中Mij为第i个模型中第j个模型;μij为第i个模型中第j个模型的概率值;μi为第i个模型集中模型概率的最大值。
(1)前时刻估计的步骤
步骤1:并行计算
输入目标状态以及状态协方差矩阵,并行执行IMM1(a-1)、IMM2(a-1)、IMM3(a-1)算法,计算得到前时刻目标状态预测向量X1(a)、X2(a)、X3(a);状态协方差矩阵P1(a)、P2(a)、P3(a);ηi(a)以及各Mij的概率μij(a)。
步骤2:比较
计算max(ηi)的值,当max(ηi)>0.75时,当前时刻即为CH时刻,所对应的模型记为G(CH)。比较ηi(CH)的值,比较μij(CH)的值,找到其中最小值所对应的模型,记为B(CH)。
步骤3:估计输出
当前时刻为CH时刻时,将ηi中最大值对应模型集的状态输出作为最终的输出,最后输出的状态估计向量为X(CH)状态协方差矩阵为P(CH),至此前时刻的状态估计结束。否则取3个模型的估计状态向量X1(a)、X2(a)、X3(a)的算术平均值作为估计输出,跳转步骤1继续执行前时刻的算法流程。
(2)第k(k=CH+1,CH+2,…)时刻的状态估计流程
步骤1:并行计算
将k-1时刻滤波结束得到的状态估计值作为先验信息提供给IMM1(k-1)、IMM2(k-1)、IMM3(k-1)中各滤波器进行并行计算。
步骤2:概率检测
模型概率检测(model probability detection, MPD)作为整个SAC-IMM算法的关键步骤,MSPT的判断是机动目标运动发生转变的关键,以及模型集更新的直接依据,具体实施办法如下:
由于该算法的设置原因会导致k时刻在IMM1、IMM2和IMM3模型集中都会存在CV-CA-CT(IMM0)模型集,设形如IMM0模型集中最小模型概率所对应的模型为B(k),如果B(k)=B(k-1)跳转到步骤5,否则进入步骤3。
步骤3:模型更新
由于该算法的设置原因,被删除的模型B(k-1)将只会出现在IMM0模型集中,当B(k-1)不再是IMM0中最小概率且满足以下条件之一:
{|μB(k)-μB(k-1)|>0.05||μB(k)|>0.3}
(20)
即认为目标的运动状态可能发生改变,模型集将会更新,各模型也将进行初始化计算,初始化的具体实施方法见步骤4。
步骤4:模型集初始化
将3个模型集恢复为初始状态(CV-CA-CT-CV、CV-CA-CT-CA、CV-CA-CT-CT),将k-1步IMM0中各模型对应的估计状态以及状态协方差初始化IMM1(k)、IMM2(k)、IMM3(k)模型集中相同的模型。
步骤5:状态输出
当目标状态更符合某一运动模型时,该运动模型被分配更多的概率,不匹配的模型分配越少的概率时估计的运动状态将会越准确,该自适应算法的状态输出分两种情况:
当B(k)=B(k-1),取ηi中最大值所对应的模型集的X(k)、P(k)作为输出结果。
否则取IMM0模型集的计算结果作为最终的估计状态并输出。至此一个循环结束,跳转到步骤1开始下一个循环。
SAC-IMM算法的流程图如图1所示,其中将虚线框内的子IMM算法视为一个整体。
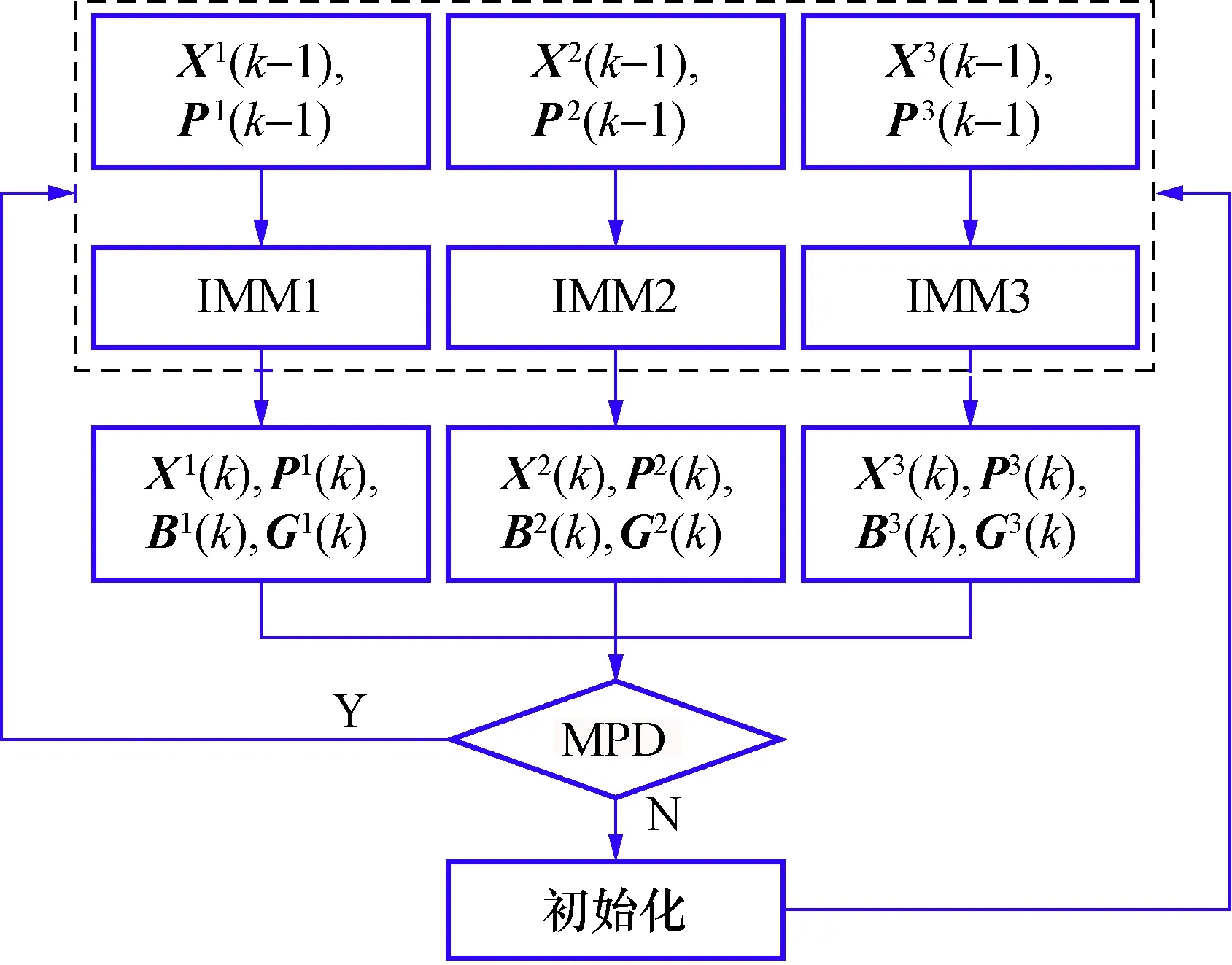
图1 SAC-IMM算法的流程图Fig.1 Flow chart of SAC-IMM algorithm
4 仿真与结果
4.1 目标运动轨迹仿真
仿真一条机动目标的行驶轨迹,设该目标初始的运动状态X(0)=[0,0,0,0,0,0],状态协方差P(0)=10000I,I为6阶单位矩阵,该目标在1 s~10 s时做10 m/s2的匀加速度运动,10.1 s~20 s时做30 deg/s的匀速度转弯运动,20.1 s~30 s时做101 m/s的常加速度运动。被测数据每0.1 s采集一次,产生的机动目标运动仿真轨迹如图2所示。
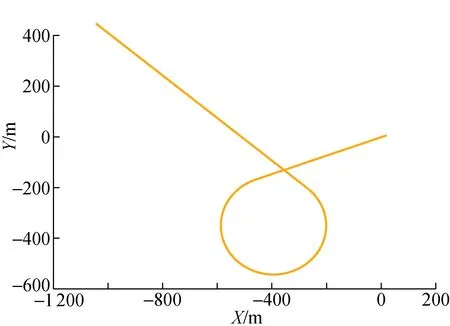
图2 目标的真实位置仿真轨迹Fig.2 Real position simulation trajectory of target
4.2 SAC-IMM算法跟踪验证
本实验对上述机动目标运动轨迹在固定模型集IMM算法以及SAC-IMM算法下应用跟踪进行了100次蒙特卡洛仿真。参考文献[16]选择GPS定位精度为5%左右,测量误差假定为白噪声序列,所以在真实值中加入均值为0、方差为(10 m)2的随机噪声得到仿真的测量值。为了证明SAC-IMM算法能够提高测量精度,将两种不同算法的滤波结果进行仿真比较。根据前文关于噪声值分析,以及状态转移矩阵P的习惯性设置,设置测量噪声方差R为(10 m)2,设置初始状态转移概率矩阵P为

图3为笛卡尔坐标系下IMM、SAC-IMM算法的跟踪轨迹。图4为图3的局部放大图。从图3可以看出交互式多模型算法能够有效地对测量值进行修正,从而使测量结果更加接近真实值,在强转弯阶段也能够准确地跟踪目标,没有发生较大的偏离。从图4的局部放大图则可以看出,SAC-IMM算法较固定模型IMM算法在位置跟踪方面可以进一步提升测量精度。

图3 不同跟踪算法跟踪轨迹对比Fig.3 Comparison of different tracking algorithms

图4 不同跟踪算法跟踪轨迹局部放大对比图Fig.4 Enlarged local comparison diagram of different tracking algorithms for tracking trajectories
4.3 讨论与分析
图5为IMM0模型集检测到的各模型的概率。

图5 模型概率Fig.5 Model probability
图6及表1分别为两种算法在CA、CT、CV状态下的位置均方根误差RMSEk比较。
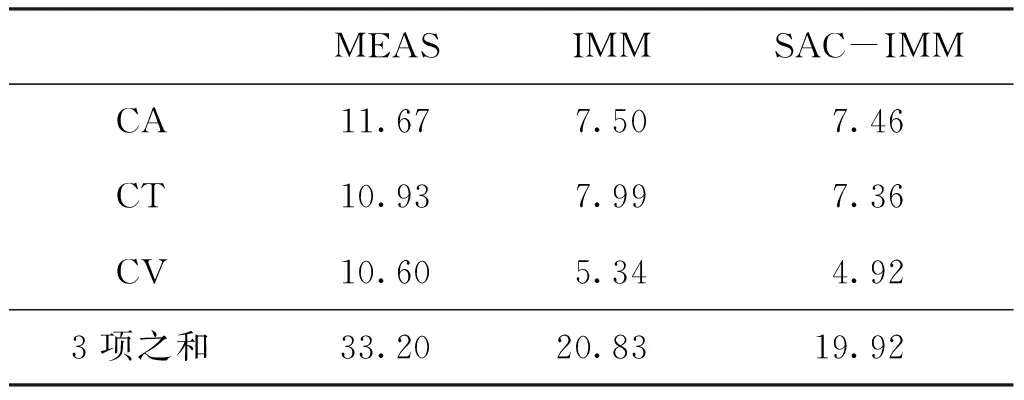
表1 位置RMSE均值Tab.1 The mean of Position’s RMSE m

图6 不同运动状态下的均方根误差比较Fig.6 Comparison of root mean square error of three in different motion states
(21)

由对比图和表1的数据中可以看出SAC-IMM算法和固定模型集IMM算法在位置跟踪精度上3项之和较测量值MEAS分别提高了37%和41%,SAC算法相比较固定模型IMM算法在位置跟踪的精度上提高了5.2%。下面分别对CV状态的非机动模式以及CT、CA状态的机动模式的位置跟踪精度以及目标运动参数获取的准确性进行讨论分析。
为了更加多方位多分析本文算法的实用性,还增加本文算法与文献[1]中提到的IMM-UKF算法在运动状态信息方面获取能力的比较分析。无迹卡尔曼滤波算法(UKF)不像卡尔曼滤波函数那样,是通过线性化非线性函数实现递推滤波,而是通过无损变换使非线性系统方程适用于线性假设下的标准卡尔曼滤波体系。在实际目标跟踪中,跟踪系统的状态模型和测量模型往往是非线性的,采用IMM-UKF算法的非线性滤波方法能够较传统IMM固定模型集算法更准确地获得目标物体的机动信息。与IMM-UKF在运动状态方面的获取的对比实验数据见表2。
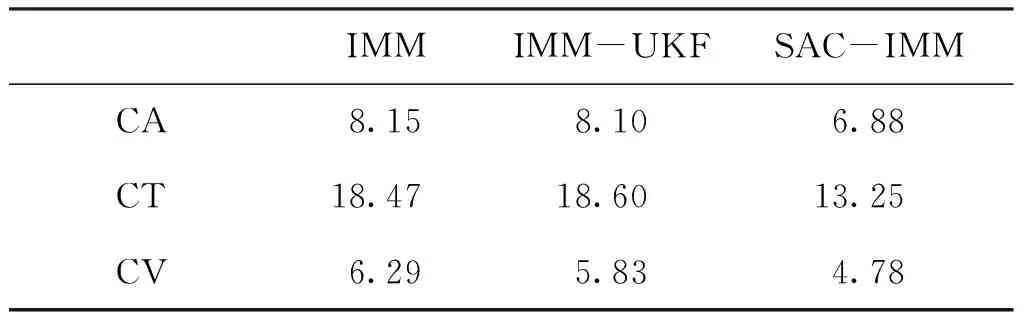
表2 运动参数RMSE均值Tab.2 The mean of motion parameters RMSE m
本文提出算法与其它算法的比较如下。在匀速运动阶段(20.1~30 s),由于目标处于非机动的运动状态,运动的速度是恒定的,跟踪较稳定不会出现较大的偏差。且模型概率检测到的G(k) 为CV,B(k)也将长时间的保持为CA,经剔除CA模型后,符合实际运动模型的CV概率将会得到提升。如表1和表2所示,两种算法在定位方面性能精度分别为0.49与0.53,且SAC-IMM较固定IMM算法在定位精度方面提升了7.9%,在速度获取准确性方面提升了24%,且相对于文献[1]中的IMM-UKF算法提升了18%。两种算法对目标运动的追踪误差均方根也较其它两种机动运动状态小,可以看出交互式多模型算法在目标做非机动运动时跟踪性能较好,且SAC-IMM算法在跟踪精度和信息获取方面相比较固定模型集IMM算法要有一定程度上的提升。
在匀加速运动阶段(0~10 s)和匀速转弯运动阶段(10.1~20 s),目标处于速度和加速大小和方向发生变化的机动状态,这对于模型检测得精度提出了较高的要求。SAC-IMM算法在这两个阶段的定位精度上分别提高了34.5%和32.6%。目标在CA状态下的时候,SAC-IMM算法相比较固定模型集IMM算法在精度方面没有提升,在CT状态下提升为7.9%。由图5可以看出在目标运动的0~10 s区间内,模型概率检测十分不稳定且模型概率的检测与实际产生偏差,在进行模型的激活与剔除存在误判,故在此阶段SAC-IMM算法的位置误差较大,导致了自适应模型集需要频繁的进行切换,在模型集进行切换的时模型概率的检测发生误判就会加大当前跟踪的误差,可见SAC-IMM算法在模型概率检测发生误判时跟踪精度将会发生下降。在目标运动的10.1~20 s区间内,模型概率检测比较稳定且模型概率的检测符合实际的运动情况,因此在此阶段应用SAC-IMM算法的位置跟踪精度得到了提升。
由图6(a)以及图6(b)可以看出SAC-IMM算法在一定程度上可以减小峰值误差,这是因为当目标的运动状态发生改变时,不匹配的模型集概率会迅速减小,自适应的模型集将会根据当前的目标运动状态匹配更加合适的模型结构,从而将会比固定模型集在得到更加准确快速的进行模型概率的分配。由表2可以得出SAC-IMM算法在获取运动目标加速度信息的准确率方面相比较固定IMM和IMM-UKF算法提升了15.6%和15.0%,在获取CT运动状态的转角信息提高了28.3%和28.8%。交互式多模型算法在目标处于机动运动状态时可以提高测量精度,SAC-IMM的自适应模型集算法能够更加准确地获取机机动目标的运动信息。
5 结 论
本文对固定模型集的交互式多模型算法进行了改进,提出了一种交互式多模型集自适应协同滤波(SAC-IMM)算法。并针对含有CV、CT、CA 3种运动状态的运动目标进行仿真和对比实验分析。从而得到以下结论:固定模型集和本文所提出的自适应模型集跟踪算法在CV、CT、CA 3种运动状态的跟踪性能都能够得到一定程度上的提升,且实时性能较好。SAC-IMM算法能够更加准确的获取运动目标的速度、加速度以及转角等信息,并且在目标状态发生转变时能够更加快速的匹配项对应的模型,减小峰值误差。在不增加模型种类的情况下,SAC-IMM算法可以实现更加精准的目标跟踪定位和运动信息的获取。

