基于多种小波变换的一维卷积循环神经网络的风电机组轴承故障诊断
陈维兴,崔朝臣,李小菁,赵 卉
(1.中国民航大学,天津 300300; 2.中国人民解放军 31439部队,辽宁 沈阳 110000)
1 引 言
滚动轴承作为风力发电机组传动链机构核心部件之一,其健康状况对于机构性能和使用寿命会有很大影响[1],因此,风力发电机组轴承的故障诊断对于机组的安全运行具有重要意义。卷积神经网络(convolutional neural network,CNN)自从在图像识别领域取得巨大成功以来,一些学者尝试将其应用于故障诊断领域[2]。如文献[3~5]提出基于一维卷积神经网络的旋转机械故障诊断算法。虽然利用一维CNN对振动信号进行故障识别方法在诊断结果上具有一定效果,但风力发电机组轴承实际运行中其振动信号呈现出非平稳、背景噪声大等特点,利用一维信号进行故障诊断的方法丢失了信号的频率信息,无法充分展现信号的时频特征。为弥补一维CNN的缺陷,Chen等[6]提出一种基于离散小波变换和CNN的故障识别方法,证明了其可行性。Li等[7]利用短时傅里叶(DFT)变换得到时-频谱样本,用CNN进行特征提取,该方法具有一定的鲁棒性。Zeng等[8]利用S变换获得的时-频图作为卷积神经网络的输入,进而提取故障特征以进行故障诊断。基于时-频信息的CNN方法虽然在定转速轴承故障诊断中取得较好的效果,但CNN是通过将局部信息聚合到全局,丢失了时-频信号的长时依赖性。由于时-频特征在时域上具有时移性、风力发电机组轴承振动信号的复杂性,单小波变换无法囊括信号的多种振动模式,使得所训练的网络在实际应用中稳定性不强。
为改进传统方法的缺点,提出基于多种小波变换的一维卷积循环神经网络(multi-wavelet-1D convolutional LSTM, Mw-1DConvLSTM)网络架构。首先利用多种小波函数得到时-频矩阵,使得信号特征得到充分展现;利用CNN提取每个时间步频率特征,再利用扩展长短时记忆网络(long short term memory network, LSTM)自适应捕获样本全局时空信息,进而实现轴承故障模式的识别。通过与传统的CNN方法对比,在复杂工况下,本文提出的方法具有更高的准确率和稳定性。
2 小波变换与ConvLSTM
2.1 小波变换
风力发电机组轴承振动信号是一种非平稳信号,其信号随时间而变化。傅里叶变换无法捕捉信号时间序列中某一特定频率出现的时间[9],因此不适合分析非平稳信号;维格纳分布虽然具有很高的时-频分辨率,但用于多个信号分量时,会产生交叉项干扰,有时会严重影响原信号[10];循环平稳信号分析虽然在机械故障诊断领域的应用取得了不少的成绩,但是在非高斯、非平稳噪声中鲁棒性较差[11];经验模式分解由于其理论不完备,缺少严密的数学基础支持,其应用还存在一些重要的问题需要解决[12];小波变换克服了短时傅里叶变换固定时-频分辨率的缺陷,避免了二次型时-频分布中交叉项对分解结果的影响,也不存在经验模态分解理论基础不完善的问题[6]。
小波变换具有很强的时-频复合观测特性,而复杂工况下(速度和负载时变)风电机组轴承振动频率观测值具有明显的时变非线性[13,14],故利用小波变换[15]实现时-频特性的提取。考虑到数据的离散采样,工程计算能力问题,实验采用离散小波变换。
2.2 ConvLSTM
ConvLSTM最初用于解决气象预测问题[16]。后因其强大的时空数据处理能力被广泛应用于视频处理任务中[17,18]。ConvLSTM是LSTM和CNN的扩展,由用卷积运算代替LSTM中的矩阵乘法,将所有的输入、输出、隐层状态和ConvLSTM门控都设置为三维张量,其中2个维度为时空信息(行和列),最后一个维度为ConvLSTM中随时间变化的状态信息。ConvLSTM的核心公式如式(1)~式(5)所示[16]。
it=σ(Wxi*Xt+Whi*Ht-1+Wci∘Ct-1+bi)
(1)
ft=σ(Wxf*Xt+Whf*Ht-1+Wcf∘Ct-1+bf)
(2)
Ct=ft∘Ct-1+it∘tanh(Wxc*Xt+Whc*Ht-1+bc)
(3)
ot=σ(Wxo*Xt+Who*Ht-1+Wco∘Ct-1+bo)
(4)
Ht=ot∘tanh(Ct)
(5)
式中:“*”为卷积操作;“∘”为哈达玛积。由于时-频图既包含频率上的空间信息,又包含时序依赖信息,而ConvLSTM能够自适应捕捉信号的空间特征和长短时依赖特征。因此,本文使用ConvLSTM进行时-频特征的提取。
3 基于Mw-1DConvLSTM的故障诊断方法
在故障诊断过程中,为了将振动信号得以充分展现和提取,提出一种基于Mw-1DConvLSTM的故障诊断方法。1) 多小波变换策略:通过多种小波基变换将原始振动信号从多个角度得到互补特征,增加数据冗余,进而增加模型的稳定性;2) 时空特征提取策略:可以从一定程度上弥补由于CNN平移不变性而造成在样本较小时容易陷入过拟合的缺点。同时,又充分结合时-频特征的物理意义,使得所训练的网络具有更好的鲁棒性。
3.1 多小波变换策略
由于风力发电机组轴承不同部位振动信号表现出的不同频率特征,使得所测得的信号是由多种频率叠加、耦合的结果。此外,轴承故障会引入低频脉冲,而这些成分易被具有主振幅的固有高频分量和强背景噪声所掩盖。因此,单一小波无法满足信号分解需求。故需要利用多种小波从多个角度提取信号的互补特征,为网络提供不同条件下的互补判别能力,使得网络具有更好的故障识别能力。
针对不同特征的信号,不同小波基的选择对于分析结果具有一定差异。需选择合适的小波基才能够满足小波分解的可完全重构性。小波函数的选择通常应从正交、线性相位、连续和紧支撑4个方面综合考虑,迄今为止,尚无一种小波函数能够同时满足需求。因此,结合风力发电机组轴承振动信号特征,在比较了几种具有良好正交性和紧支撑的小波基后,根据其分解重构误差,重构误差计算公式(如式(6))。最终选定db3、coif1和sym2小波函数对原始振动进行“同源异构变换”,如图1所示。
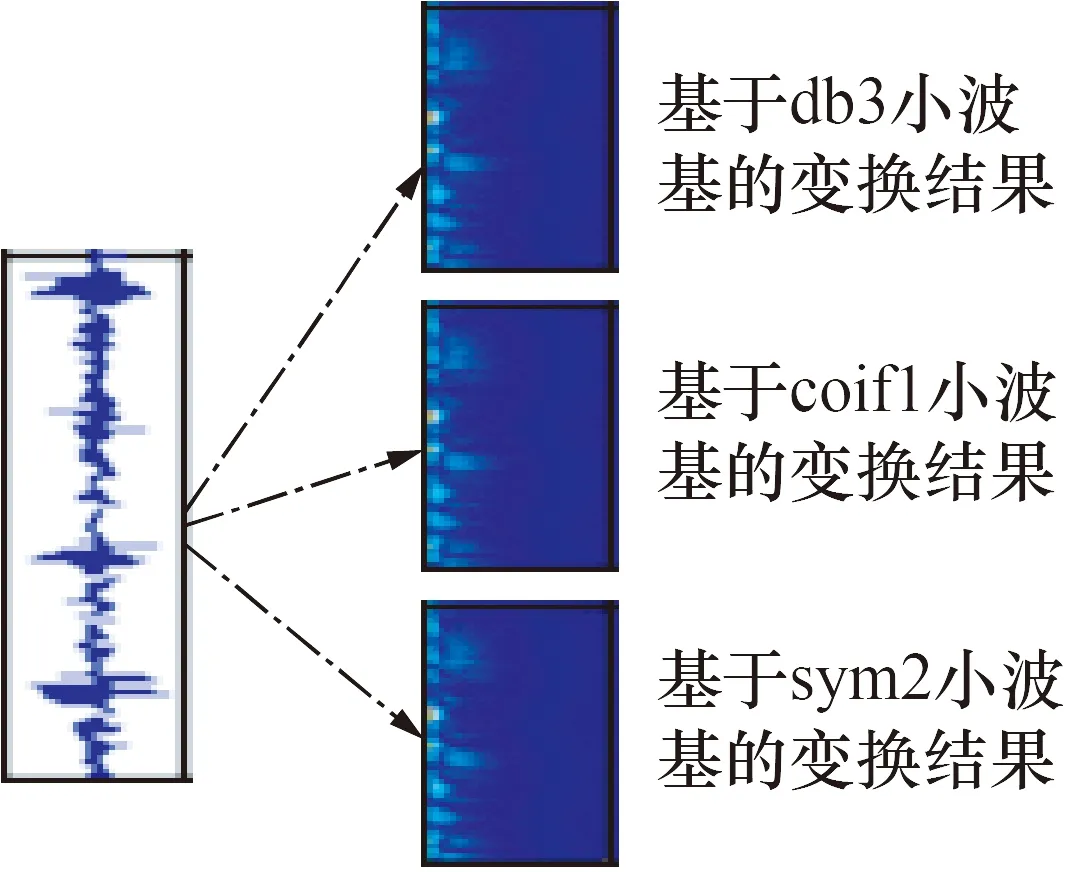
图1 多小波变换Fig.1 Multi-wavelet transform
(6)
式中:srec,i为经小波函数重构后得到的重构信号;s为原始信号,i∈(1,2,…,n)为信号序列。
3.2 时空特征提取策略
传统CNN将得到的时-频矩阵视为图像,然后卷积神经网络对信号进行多层特征提取,实现特征表达[19]。但由于CNN在处理大尺度特征时,平移不变性效果不理想[20]。如图2所示,卷积层使用3×3的卷积核,池化层使用2×2的池化块;输入层部分3×3区域对应于卷积层中的一个输出元素,卷积层的输出经过2×2区域的最大值池化层产生一个输出元素。基于此过程,如图3所示,最大值池化最左端灰色部分的一个输出元素值仅受输入层最左端4×4的灰色区域影响,其右端区域未参与计算。类似地,最大值池化最右端灰色部分的一个输出元素仅受输入层最左端4×4的灰色区域影响。虽然CNN所学习到的特征可以通过全连接层聚合到全局,包含有时-频信号一定的位置信息,有助于网络对故障的诊断。但对于具有长时依赖和周期性的轴承振动信号而言,在样本较少的情况下,网络容易陷入过拟合,泛化能力不强,最终影响模型的稳定性。因此,需要一种策略改善上述CNN方法的不足。
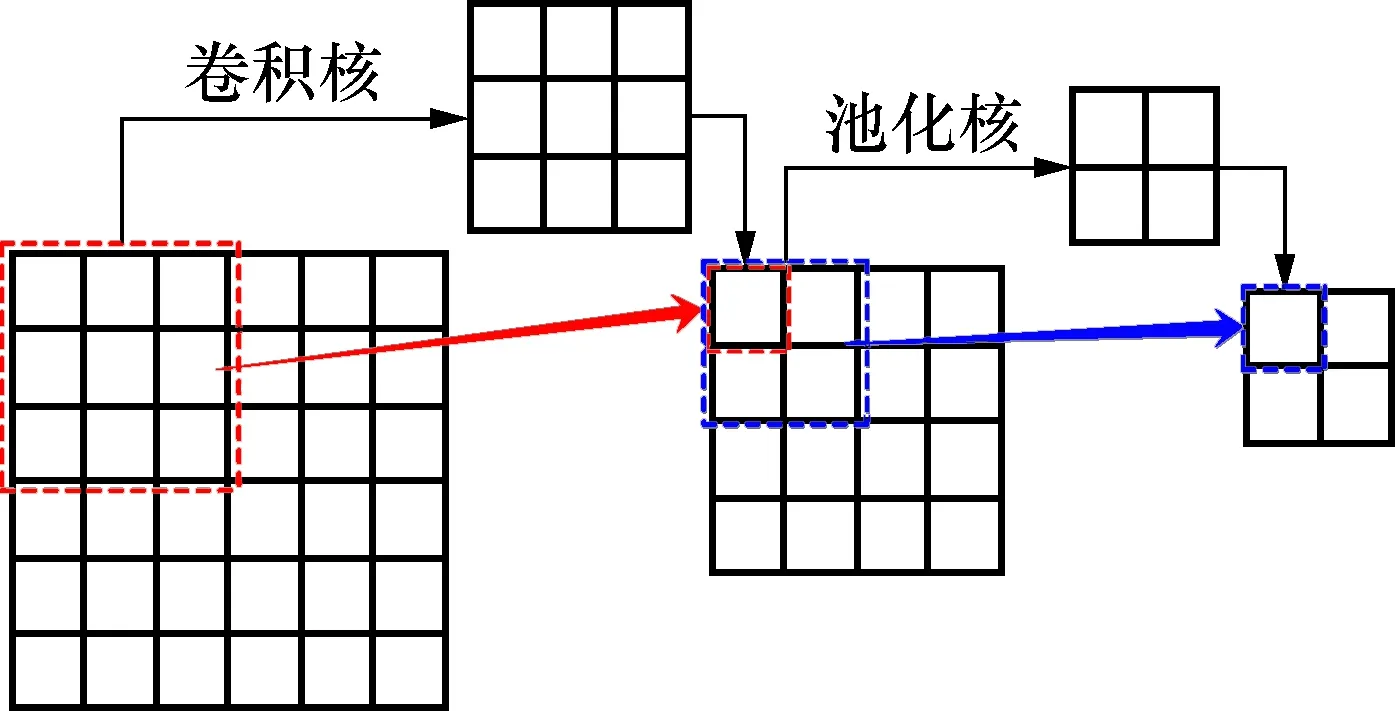
图2 卷积操作和池化操作示意图Fig.2 The schematic diagram of convolution operation and pooling operation
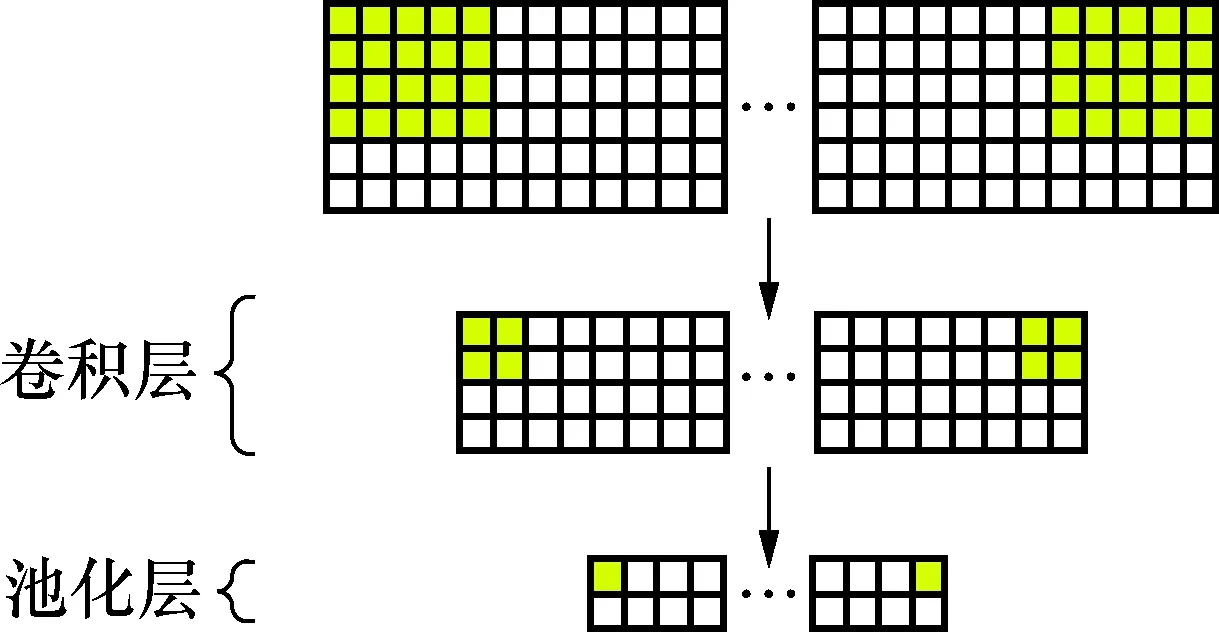
图3 CNN平移不变性示意图Fig.3 The schematic diagram of CNN translation invariance
因此,本文提出一种改进的ConvLSTM网络。该网络既结合CNN提取空间特征能力的优点,又兼顾LSTM可以访问时序信号先验知识的特性,充分考虑时-频谱包含的频率和时序双重特性。同时,由于风力发电机组轴承振动信号是一个时间序列,经小波变换后,将获得时-频谱定义为一种时空序列问题,即在某一时刻的频率分布视为空间特征,当截取某段时间空间特征时,其在时域上的趋势定义为时序特征。基于此,利用一维CNN提取每一时刻的频率特征,利用扩展的LSTM提取频率信息在时间域所呈现的时序特征,使网络在频域和时域都具有描述信号特征的能力,充分利用信号时空信息。
该策略的核心部分为样本特征的自适应提取。方法如下:假设某小波变换得到的时-频谱分为N个样本,每个样本为S1,S2,…,SN,每个样本包含T个时间步,则第1个样本可表示为S1={f1,f2,…,fT}。于是对于第1个样本特征提取步骤如下:首先利用一维CNN提取每一帧空间特征,即单个时间步所包含的频率信息;由于每一帧之间的频率变换在时域上具有一定的关联性,因此利用扩展的LSTM自适应地捕获各帧间的时空特征,实现网络对样本全局时空特征的自适应学习,如图4所示,图4中,xT表示在T时刻的输入,ck,T-1表示T-1时刻第k层网络的状态单元,hk,T-1表示T-1时刻第k层网络的隐层状态。
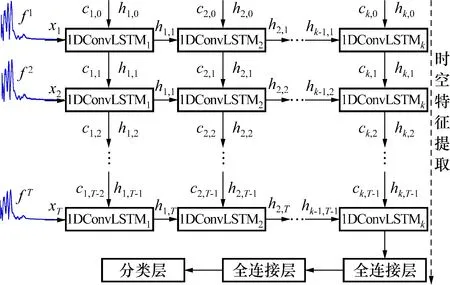
图4 样本时空特征提取Fig.4 Temporal and spatial feature extraction of sub-sequences
4 故障诊断方法流程
基于Mw-1DConvLSTM的故障诊断流程如图5所示,其具体流程步骤如下:1) 原始振动信号采集与分割:采集轴承振动信号,并将振动信号进行等长分割;2) 将分割好的信号进行多种小波变换得到时-频谱;3) 设置网络超参数,并初始化网络权值、偏置及全连接层的权值和偏置;4) 将数据批量输入网络,最后通过全连接层和分类层获得与故障类型相对应的one-hot编码形式的标签,计算出误差。用反向传播的方法将误差回传,更新网络权值和偏置,进行训练;5) 重复第4)步,直到网络达到一定精度或达到所设定的迭代次数,最后将训练好的模型进行保存,并进行故障诊断。
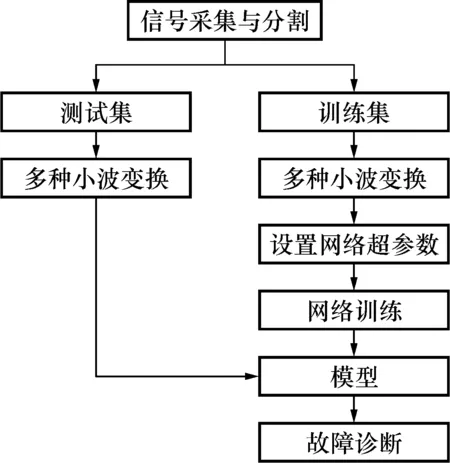
图5 基于Mw-1DConvLSTM的轴承故障诊断流程图Fig.5 Flow chart of bearing fault diagnosis based on Mw-1DConvLSTM
5 实验设计
5.1 实验描述
本文实验数据来源于山东某风场华锐SL1500型风机佳木斯发电机驱动端6328型轴承和永济发电机驱动端6332型轴承的振动信号,由安装在风机上的CMS系统采集获取,系统采样频率为25.6 kHz。图6分别展示了CMS系统的振动传感器的安装位置(具体位于发电机驱动端的端盖处)和风力发电机组的基本结构。

图6 CMS系统发电机轴承传感器测点布置示意图Fig.6 Schematic diagram of measuring point arrangement of CMS system generator front-end bearing sensor
5.2 数据集描述
实验数据分为3种不同的转速,每种转速都有四种不同类型的运行状态,即正常状态、外圈故障、内圈故障和混合故障,如图7所示。佳木斯驱动端轴承的振动数据包含6 900个样本,每个样本信号长度包含2 048个数据采样点,用其中6 000个样本作为训练集,900个作为测试集。用900个永济发电机轴承的振动数据样本作为验证集,检验模型的泛化能力。具体样本信息如表1和表2所示。

图7 轴承的健康状态类型Fig.7 Healthy state type of bearings
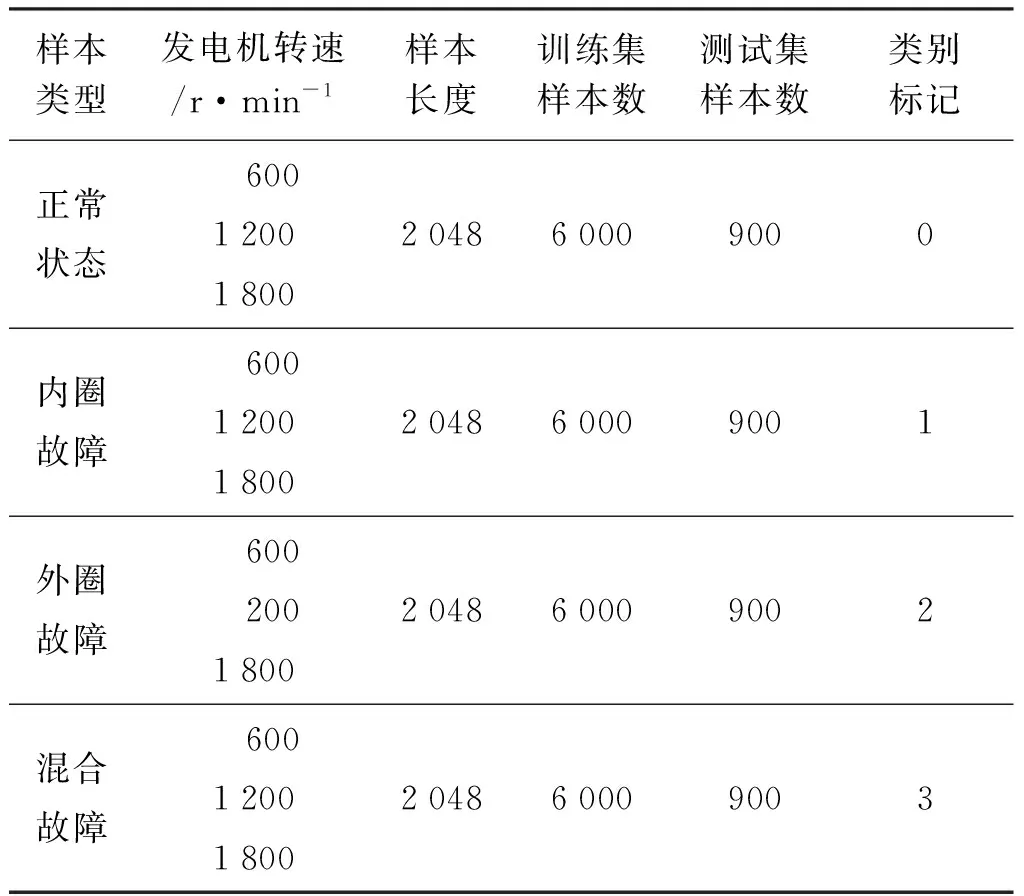
表1 佳木斯发电机样本信息描述Tab.1 Description of Jiamusi generator sample information
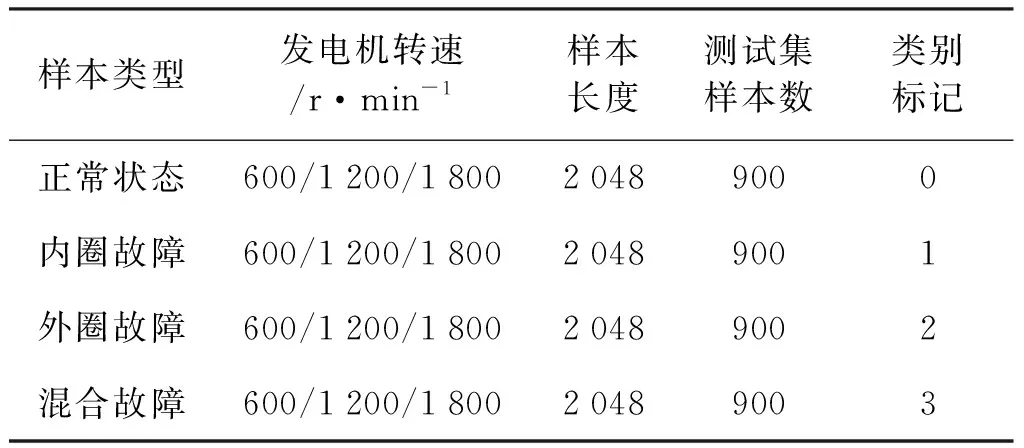
表2 永济发电机样本信息描述Tab.2 Description of Yongji generator sample information
6 实验结果
实验基于Keras平台,采用交叉验证进行对比,得到最优的网络参数。每层的激活函数设置为“relu”,最后一层激活函数为“softmax”;采用交叉熵作为损失函,“Adam”作为优化器。
6.1 评价指标
为对所提模型性能进行量化评估,使用准确率、查准率、召回率和F1-score作为网络评价指标[4],各指标具体计算公式如下:
(7)
(8)
(9)
(10)
其中:PT为某一类样本被正确分类的数目;NT为其它类别被正确分类的数目;PF为该类别被错误分类的数目;NF为其它类别被错误分类的数目。
6.2 参数配置
6.2.1 小波函数选择
根据式(6)计算不同小波函数的重构误差,选择适用于风电机组轴承振动信号的小波函数,如表3所示。最终选择Harr、coif1、db3和sym2这4种重构误差较小的小波函数进行实验。

表3 不同小波函数的重构误差Tab.3 Restructuring Error in Different Wavelet Functions
6.2.2 网络深度和样本长度设置
所提模型网络深度和样本长度对模型的诊断性能具有重要影响。为保证在较高诊断正确率的同时,不会因为参数增加而使网络难以训练。经过多次试验对比后,选用如图8的网络结构,样本长度选择2 048个采样点。使用多个通道并行输入进行特征提取,经过1DConvLSTM层后将特征进行跨通道融合,实现多种小波时-频特征的提取。为了降低数据维度加快训练难度,增强网络的泛化能力,在最后一个1DConvLSTM层后,将2 048×64×1维特征,通过一维全局最大值池化实现维度约简,代替全连接层;最后将得到的特征表达通过softmax层实现网络分类。网络具体参数如表4所示,其中,表中1DConvLSTM阶段只列出一种小波通道的参数,另外两个通道配置与之相同。Ks表示卷积核的大小,F表示卷积核深度,S代表步长。

表4 网络参数配置表Tab.4 Network parameter configuration table
6.3 实验结果分析
6.3.1 多小波时频分析与单一小波时频分析
振动信号在不同小波变换下提取的特征差异较大,因此有必要考虑多小波分解特征。为了验证小波分解数目对于准确率的影响,使用1~4种小波进行实验验证。实验采用图8所示的结构。不同条件下的实验结果如表5所示。
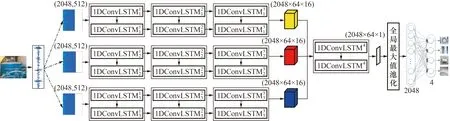
图8 基于Mw-1DConvLSTM的轴承故障诊断网络结构Fig.8 Bearing fault diagnosis network structure based on Mw-1DConvLSTM
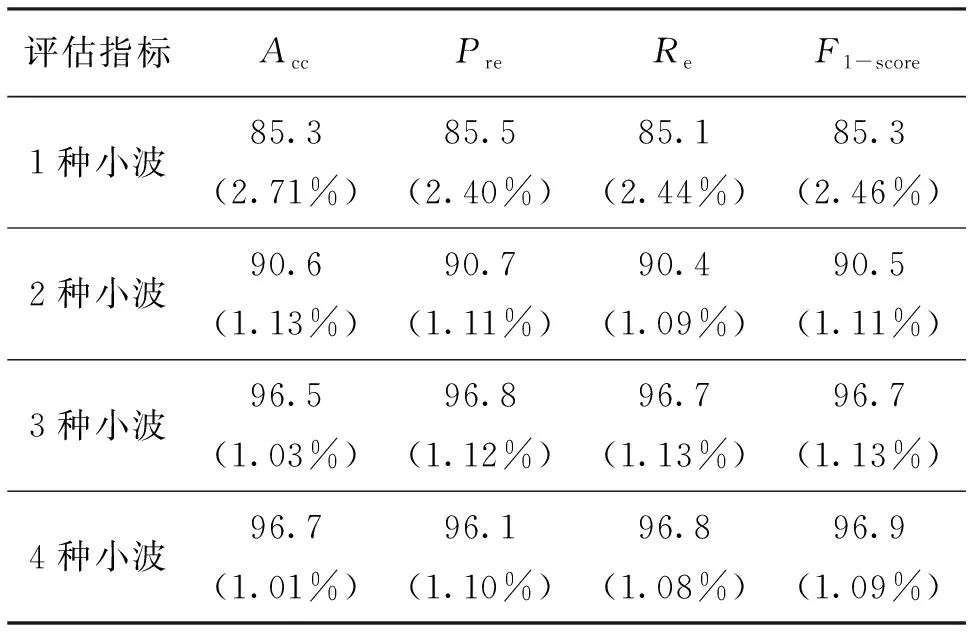
表5 多种小波数目诊断性能比较Tab.5 Comparison of diagnostic performance of various wavelet numbers
由表5可以发现本文方法在2~4个类别数目上的性能优于传统的单一小波方法。一般来说,随着数目的增加,模型可以获得更稳健的性能,因此所提出的多小波方法可以提高诊断性能。同时,可以发现当利用3个小波时取得较好的效果,利用4种小波时,诊断性能并没有得到较大提升,却会增加网络训练时间,因此最终选用coif1、db3和sym2这3种重构误差最小的小波函数。
为更直观地理解多小波特征融合的优越性,使用t-SNE降维技术对数据特征进行可视化。图9(a)为原始数据,可以发现原始数据不具有分类特性;图9(b)为将单一小波数据经过网络特征提取后可视化的结果,可以发现模型有一定的聚类趋势,但类间区分不明显;图9(c)为将2种小波数据经过网络特征提取后的结果,可以发现具有一定的聚类和分类特性,但分类效果不明显;图9(d)为将3种小波数据经过网络特征学习后的结果,可以观察到,此时网络提取的特征已经表现出良好的聚类和分类特性。可以推断出随着小波种类数目的增加,相同健康状态的特征呈现出很好的聚类特性,不同健康状态间呈现出更好的分类特性。结果表明3种小波变换提取的特征具有较强的辨识能力。进一步验证了融合多种小波特征可以提高特征学习能力。
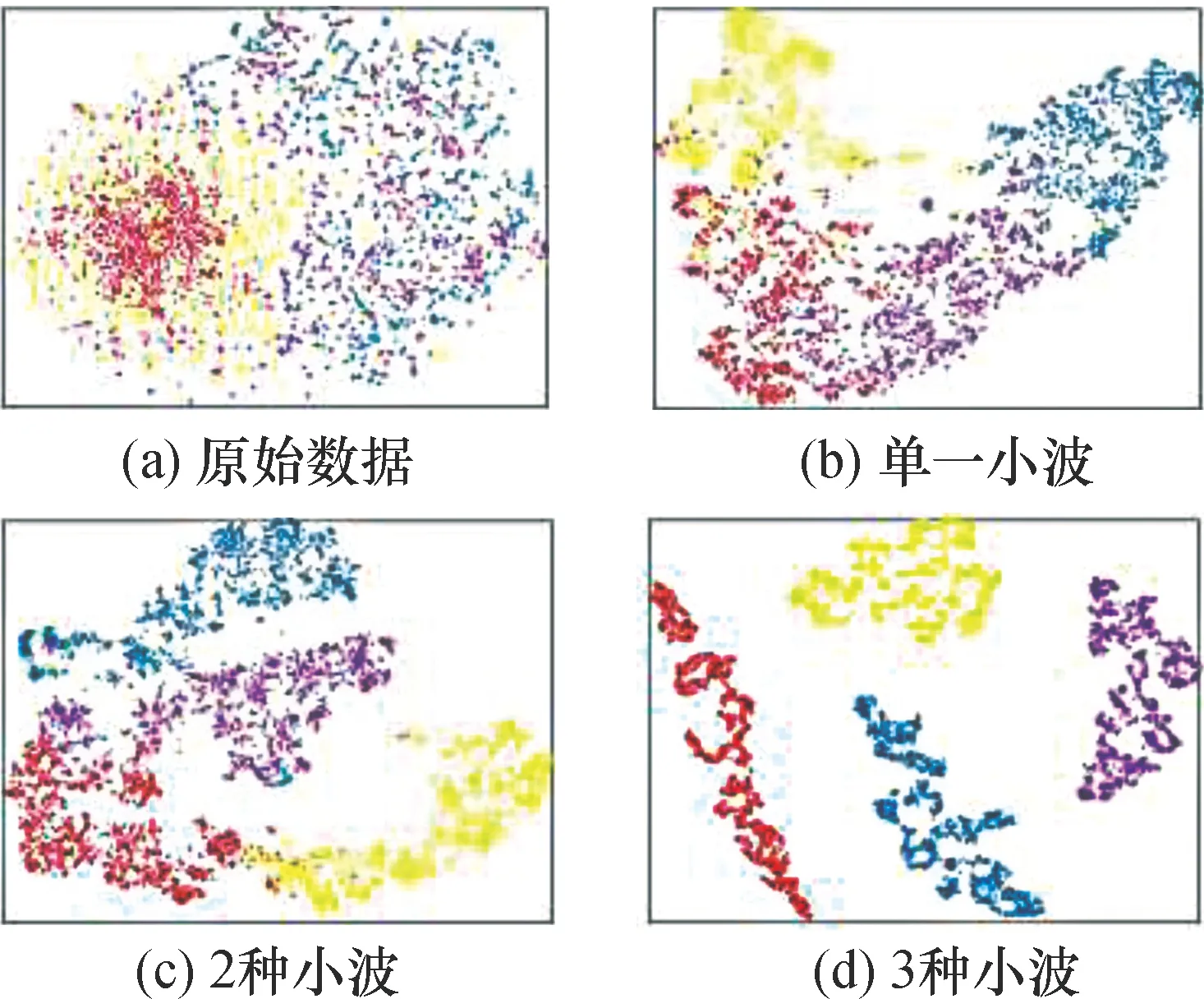
图9 不同小波数目基于t-SNE的特征可视化Fig.9 Feature visualization based on t-SNE with different wavelet numbers
6.3.2 与传统CNN方法对比
为说明本文方法在大尺度和时序依赖问题上的优越性,使用本文方法与文献[3]、[6]和[7]所述方法进行对比分析,以验证所提方法的有效性,如图10所示。观察图10可以发现,由于一维信号不能充分利用信号的频率特征信息,基于原始振动数据的卷积神经网络(简称为ACNN-FD)在实际应用中并不能取得较好的效果。基于短时傅里叶变换(简称为STFT-CNN)取得相对较好的效果,但由于机组并不能运行在理想的恒定转速状态,而是在恒定转速周围具有一定的波动性和噪声,加之短时傅里叶变换测不准原理的缺陷,使得其在实际应用中的表现并没有基于小波变换的卷积神经网络(简称为WT-CNN)的性能优越。STFT-CNN和WT-CNN相对于ACNN-FD具有较好的性能,但由于CNN网络机制的限制,其在大尺度具有时序依赖的信号处理中,效果并不理想。而所设计的Mw-1DConvLSTM由于采用了多种小波互补机制使得网络能够充分提取信号时频特征。同时,得益于本文所提的时空特征提取策略,使得网络不仅能够自主提取频域特征,而且能够提取频率在时序上的依赖特征。因此,Mw-1DConvLSTM在处理具有非平稳性的数据时,具有良好性能。
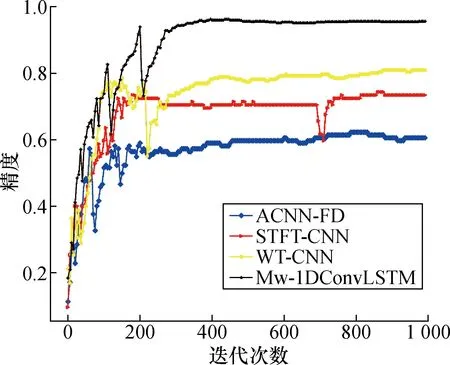
图10 不同方法精度对比Fig.10 Precision comparison of different methods
6.3.3 工况适应性实验
在实际机组运行中,转速处于波动状态,因此需要模型具有良好的泛化性。实验采用某一转速数据作为训练集,用另外2种转速的数据作为测试集。实验数据分组如表6所示,分别进行20次训练与验证,以获得较稳定的结果,实验结果如表7所示,可以发现使用单一转速振动信号进行训练在不增加样本时,本文方法仍具有良好表现,说明Mw-1DConvLSTM具有较好的转速适应性,在实际应用中对数据集的要求相对较低。

表6 不同转速实验数据集分组Tab.6 Grouping of experimental data sets at different speeds

表7 不同实验组结果Tab.7 Results of different experimental groups
6.3.4 泛化性实验
1) 不同型号发电机同一种转速适应性实验
为了进一步验证模型的泛化能力,在同一种转速下,使用佳木斯发电机轴承振动数据作为训练集,永济发电机轴承振动数据作为测试集进行验证。实验结果如图11所示,对不同型号的发电机进行诊断时,采用本文提出的方法仍然能保持很高的准确率,远高于使用文献[3]、[6]和[7]提出的方法。
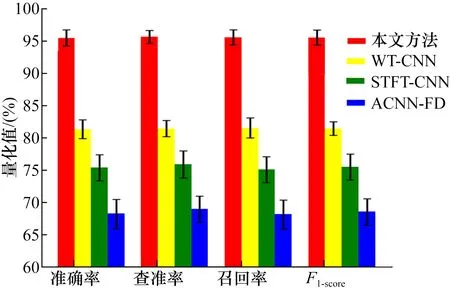
图11 不同型号相同转速下实验结果Fig.11 Experimental results at the same speed of different models
2) 不同型号发电机不同转速适应性实验
为进一步验证实际工程环境中网络模型的实用性,使用特定转速下佳木斯发电机轴承振动数据作为训练集,另外2种转速下永济发电机轴承振动数据作为测试集进行验证,如图12所示。可以发现模型在不同型号发电机不同工况下,具有较强的稳定性。
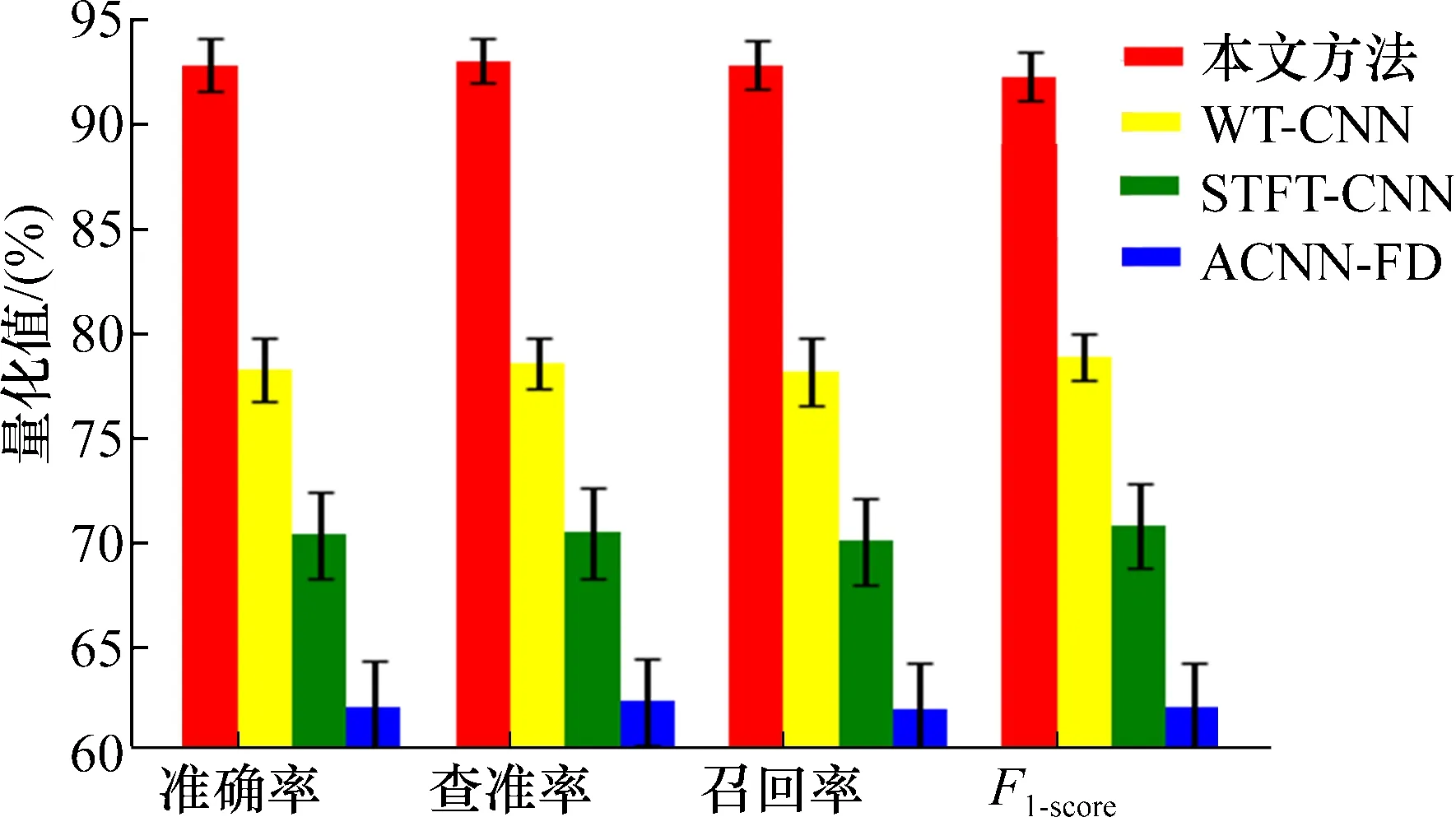
图12 不同型号发电机轴承不同转速泛化性验证Fig.12 Generality verification of generator bearings of different types
7 结 论
Mw-1DConvLSTM网络能够自适应地从多种小波变换后的时-频域信号中提取有效的时空信息,克服了基于CNN的方法不能有效提取时序信息的缺点。通过对现场实际运行的数据进行测试,可以得出以下3点结论:1) 由于1DConvLSTM能够从充分考虑时-频信号时空特征,使得在诊断过程中,网络不仅具有较高的故障识别率,在轴承信号和转速发生改变时,仍具有较高的识别率;2) 得益于多个小波变换的冗余时-频特征,使得所训练的网络相对于单小波时-频特征作为输入时,具有更高的准确率;3) 需要指出的是本文方法仍存在不足之处,相对于传统的CNN方法,Mw-1DConvLSTM网络的训练时间较长,且在训练过程中需要占用大量计算机资源,这也是下一步需要重点解决的问题。

