多边法坐标测量系统中解算方式对测量精度的影响研究

孙 威，缪东晶，李建双，姚 燕,钟 文，赫明钊，李连福

(1. 中国计量大学 计量测试工程学院，浙江 杭州 310018；2. 中国计量科学研究院，北京 100029)

1 引 言

随着现代装备制造业的飞速发展，航空航天、轨道交通、船舶等大尺寸装备领域都对制造精度、装配精度提出了更高的要求[1～6]，人们对大尺寸计量学的兴趣也日益浓厚。多边法作为一种坐标测量方法，具有大尺寸、柔性、动态测量等优点，且仅需测量长度量，避免了引入角度量测量带来的误差，继而解算出被测物体的位置坐标，具有较高理论精度[7]。

提高多边法测量精度的主要途径是寻求系统的最优布局以及通过长度标准、平面标准等进行优化约束。Takatsuji T等[8]在三维空间坐标测量系统自标定中提出了一种布局限制条件。林永兵等[9]研究了4路激光跟踪干涉三维坐标测量系统的最优布局，并且指出了影响系统自标定精度的多种因素。范百兴等[10]引入三维位置几何精度衰减因子(position dilution of precision，PDOP)，可以避开不利位置与方向，提高测量精度。Miao D等[11]提出一种采用标准长度约束的自标定算法，增加标准长度约束在优化函数中的权重值，较好地提高了系统的自标定精度与坐标测量精度。Zhang F 等[12]提出一种基于标准平面约束的标定方法，在不增加未知量的情况下，用标准平面约束来提供更多的方程。从研究现状看，对于多边法测量精度的研究较少涉及到多边法理论自身解算方式的影响，而多边法坐标测量系统彼此间的测量模型存在一定差异，对坐标解算方式的研究同样存在以下区别：①通过目标点冗余将各自的测量模型转化为非线性最优化问题进行多边法坐标测量系统参数的标定，标定完成后再进行测量；②以文献[13]为代表的多边法测量模型解算方式，将测站坐标和目标点坐标均视为未知量，通过同步解算方式由测量模型输出。二者都能完成目标点坐标的求解，但对于同一测量模型而言，涉及到的不同解算方式对测量精度的影响研究则较为缺乏。

本文针对上述情况，建立了多边法坐标测量系统测量模型，分析了多边法坐标测量系统目标点坐标两种解算方式的差异，通过对典型的4台测站多边法坐标测量系统的仿真实验，分析了两种解算方式对测量精度的影响，并进行了坐标测量精度验证实验，对进一步优化系统测量精度以及指导最优测量策略具有积极的参考意义。

2 多边法坐标测量系统测量原理

多边法坐标测量系统是通过空间中目标点到3个或3个以上已知点的距离来确定目标点的坐标，工作原理如图1所示，图1中，LT1、LT2,…,LTm为激光跟踪干涉仪。

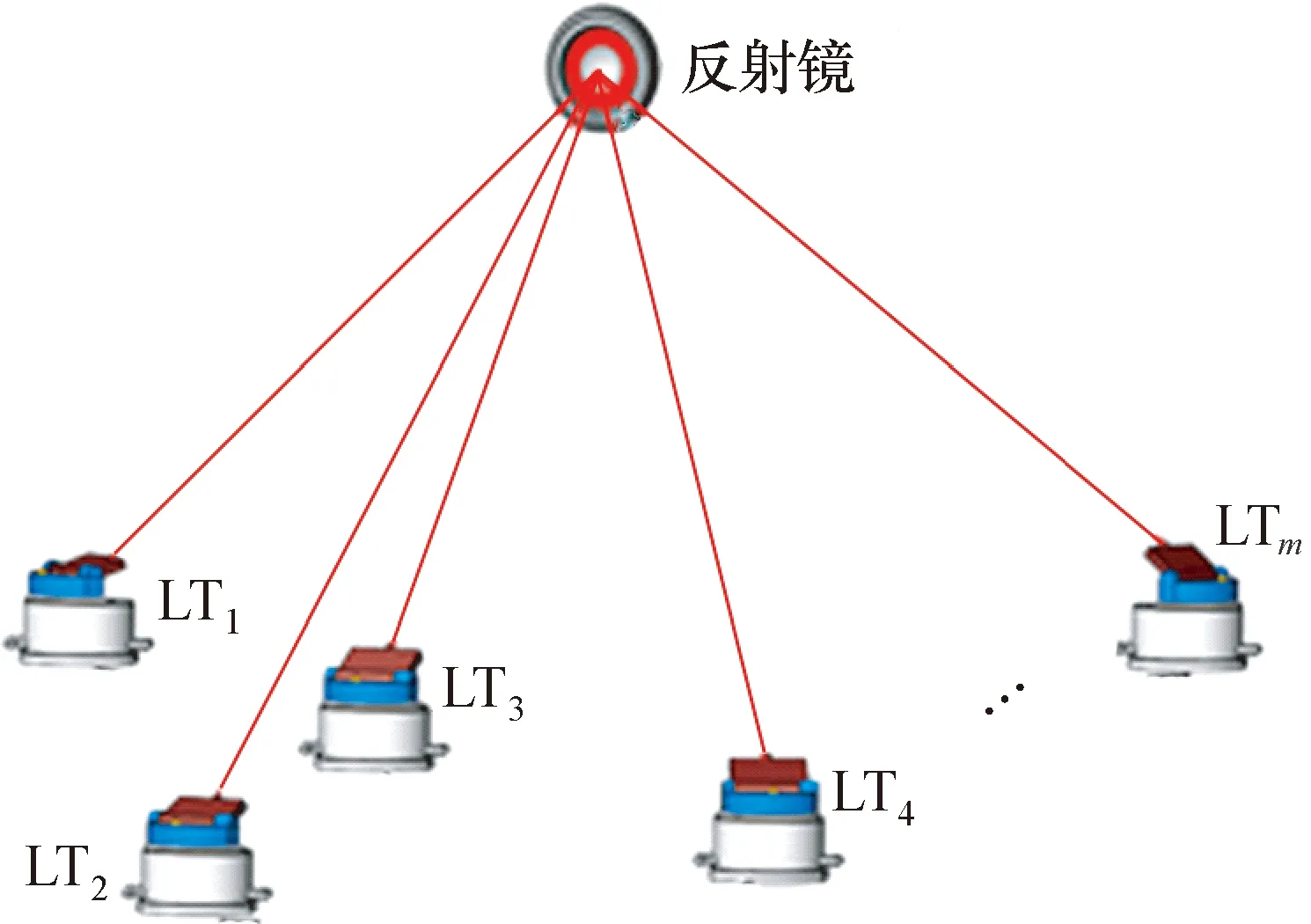
图1 多边法坐标测量系统Fig.1 Multilateral coordinate measurement system

对于空间中任一目标点Pi(xi,yi,zi)和m台测站的测量中心坐标Sj(xSj,ySj,zSj)存在如下关系式：

fi,Sj=(xi-xSj)2+(yi-ySj)2+(zi-zSj)2-

(lSj 0+ΔlSj i)2,j=1,…,m

(1)

式中:fi,Sj为两点间距离的计算值和测得值之差；i为目标点个数；lSj 0为各测站到初始点的初始长度；ΔlSj i为激光干涉测得的长度变化量；通过增加目标点数，使得方程个数大于未知量个数，将其转化为非线性最小二乘问题来处理，在目标点数i≥9，测站数m≥4时可以通过信赖域法、Gauss-Newton法、Levenberg-Marquardt等方法进行求解[14]。

需要指出的是，多边法坐标测量系统可以通过以下两种方式解算目标点坐标。

(1) 如式(1)所示，多边法坐标测量系统在m个测站测得到i个目标点的距离值是测量模型的输入量，而i个目标点的坐标以及m个测站的坐标为测量模型的输出量。测站坐标Sj(xSj,ySj,zSj)与目标点坐标Pi(xi,yi,zi)可以作为未知量，所建立的方程数量大于未知量数量时，通过非线性最小二乘问题同步解算出所有未知量，即标定过程包含在测量过程中，不单独对系统参数进行标定。

(2) 预先对多边法坐标测量系统参数进行准确标定，根据标定后的系统参数对目标点坐标进行求解。系统参数在标定过程中主要受测站布局等非线性因素的影响，可以在标定过程中加入标准长度约束[11]或者标准平面约束[12]，以提高系统参数标定精度。

坐标求解示意图如图2所示，对于任一目标点Pi(xi,yi,zi)和3台测站(A,B,C站)的测量中心坐标(xm,ym,zm)，两者并非完全独立，可以由两点间距离公式解得测站坐标与目标点坐标Pi(xi,yi,zi)的关系。

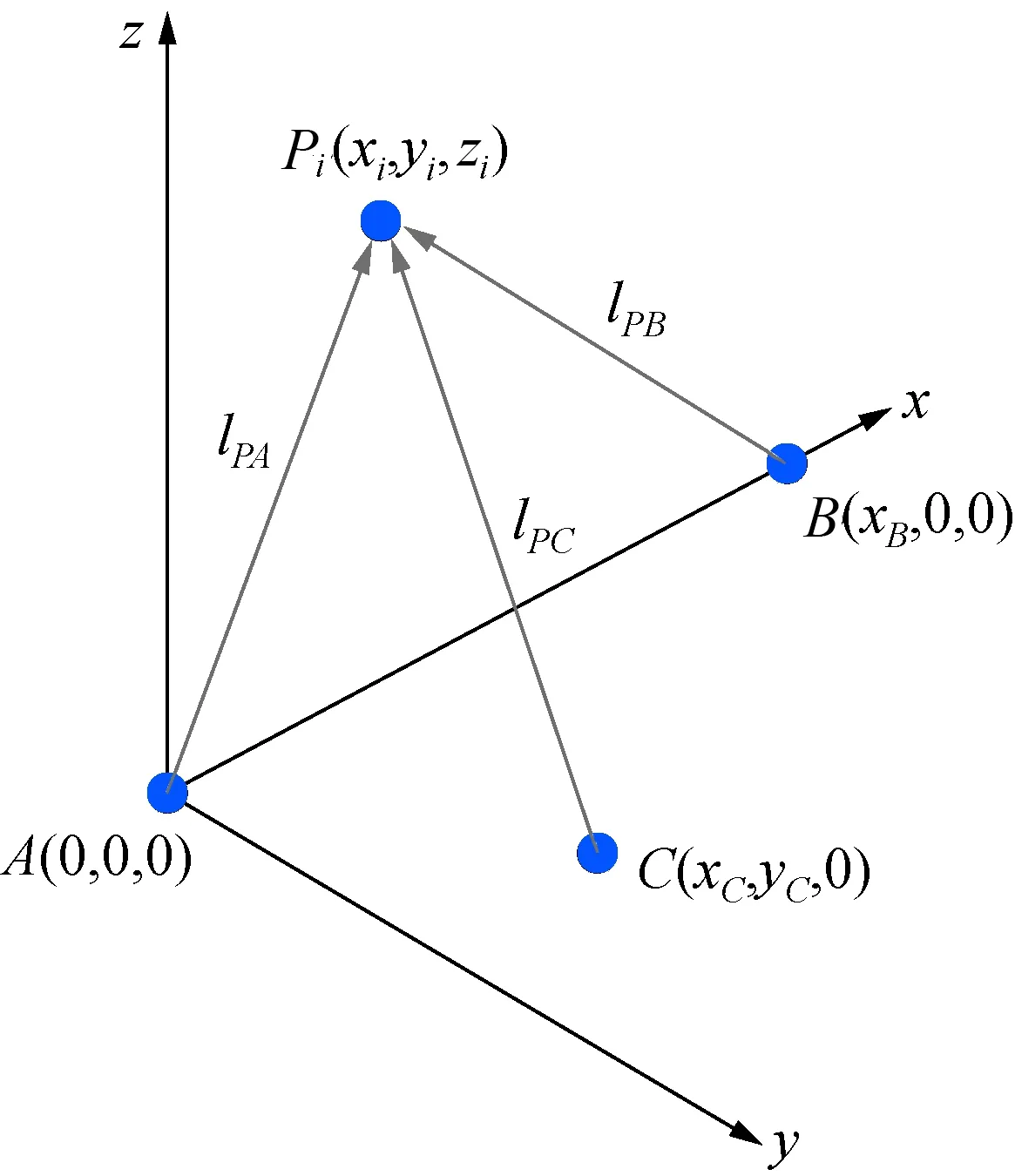
图2 坐标求解示意图Fig.2 Schematic of coordinate solution

目标点Pi(xi,yi,zi)的各坐标值公式为

(2)

将式(2)代入式(1)，这样就可以消去目标点坐标的未知量，仅对测站坐标及初始长度等系统参数进行标定，根据标定后的系统参数对目标点坐标进行求解。

3 两种解算方式对测量结果的影响

3.1 两种解算方式测量仿真实验

为了研究目标点坐标的预先标定系统参数和同步解算方式对测量结果的影响，对典型的4台测站多边法坐标测量系统分别进行了两种解算方式的测量仿真实验。如图3所示，S1，S2，S3，S4为4台激光跟踪干涉仪测量中心。令S1为系统坐标系原点，坐标单位为mm，S2点坐标为(1 964，0，0)，S3点坐标为(1 452，4132，0)，S4点坐标为(-777，638，-684)，任意3台测站构成的平面均不穿过被测面。在空间3 m×3 m×4 m的矩形区域内均匀创建3层散点，第1层为P1至P9，依次进行编号，3层共27个点。

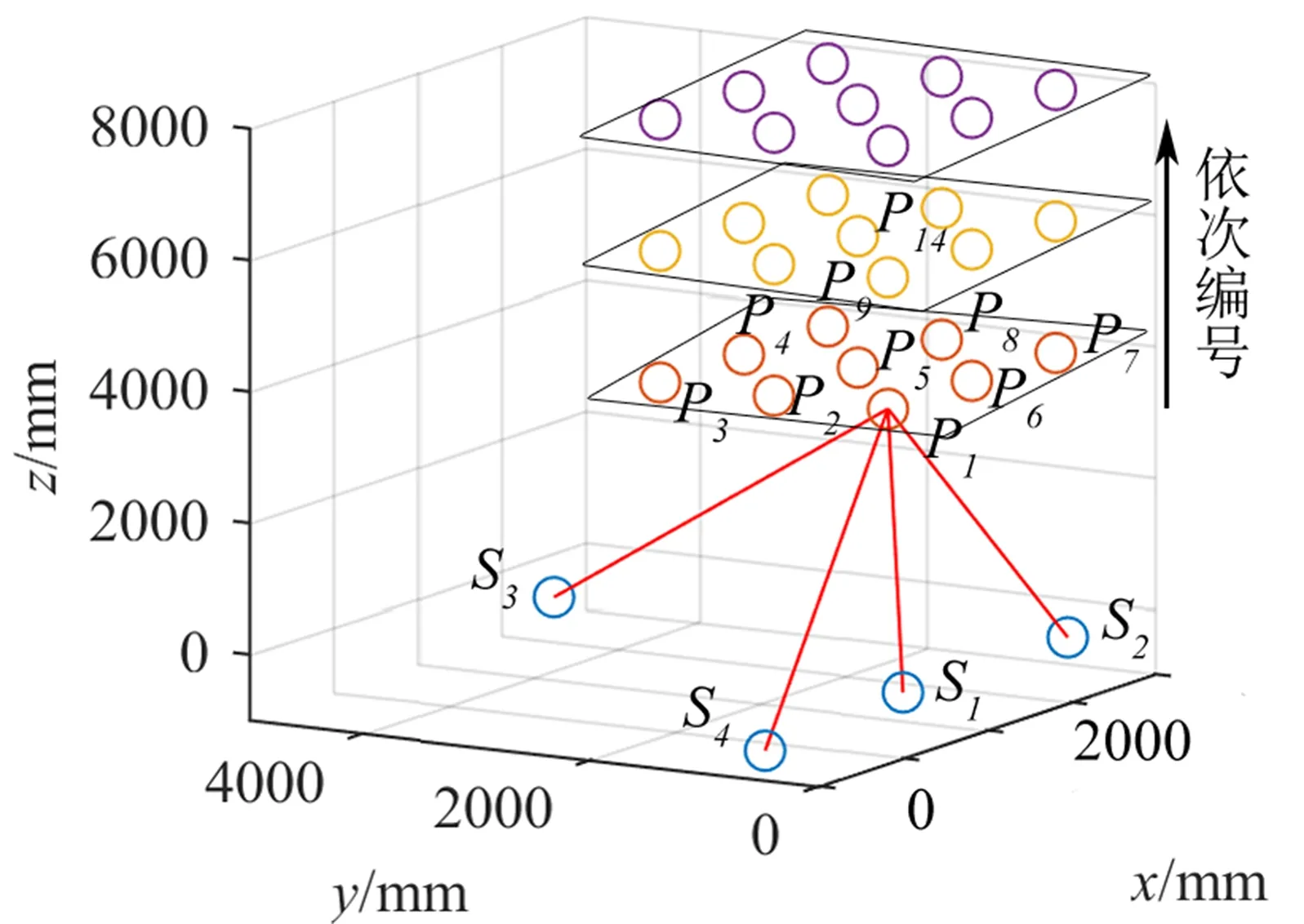
图3 仿真实验示意图Fig.3 Schematic diagram of simulation experiment

初始坐标点P1到4台仪器S1，S2，S3，S4的初始长度，以及每个点到4台仪器S1，S2，S3，S4与初始长度的变化量作为理论测长数据。在仅考虑仪器测距误差影响因素的情况下，根据激光跟踪干涉仪的测距不确定度U=0.2 μm+0.3 μm/m，对生成的理论测距值加入[-U,+U]范围内的随机噪声，作为仿真测距值。以生成的理论目标点间的12段距离值作为参考距离值L0，通过两种解算方式分别解算出目标点的坐标，由两点间距离公式计算目标点间距离值L1、L2作为测量值，分别计算L1、L2与L0的偏差作为测量误差，进行比较。

3.2 仿真实验结果分析

两种解算方式的3组测量仿真实验结果如图4所示。

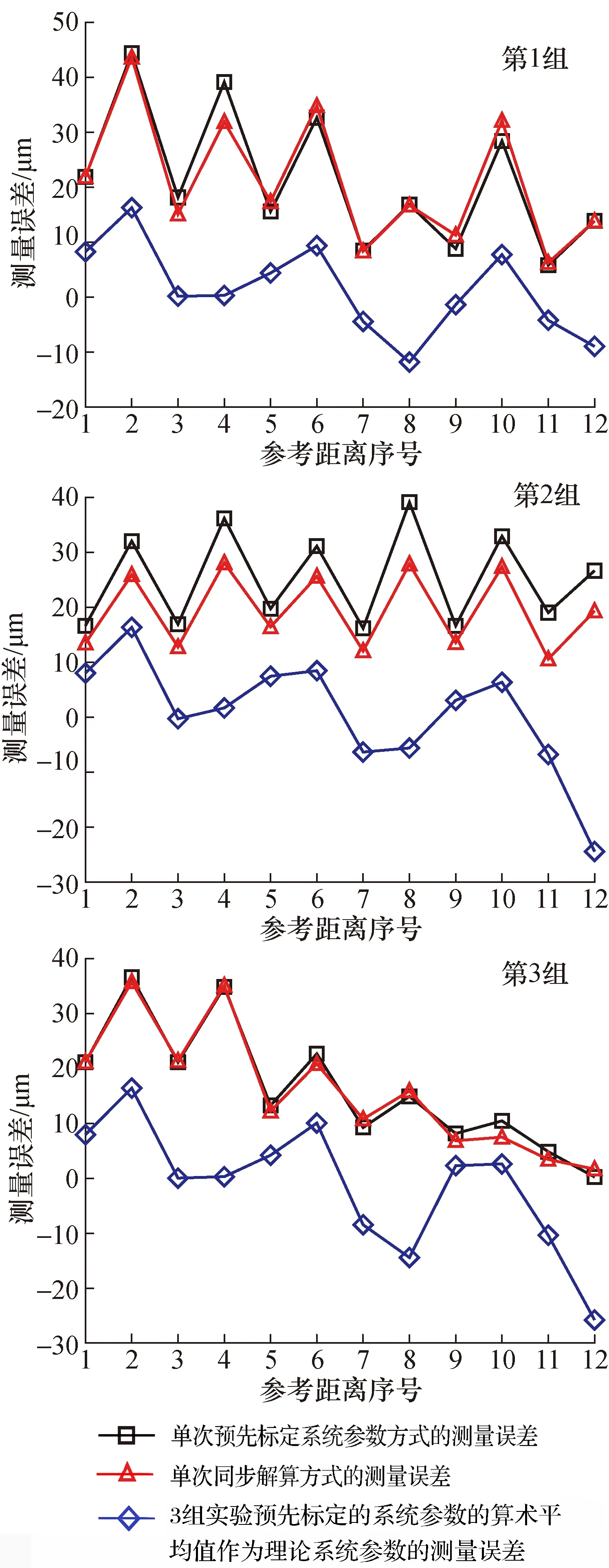
图4 测量仿真实验结果Fig.4 Measurement simulation results

3组实验结果中，单次预先标定系统参数与单次同步解算方式的测量误差范围及趋势均较为接近。其中，第1组实验单次预先标定系统参数测量误差分布在[5.7 μm，44.1 μm]范围内，误差平均值为21.0 μm，标准差为12.4 μm；单次同步解算方式测量误差分布在[6.4 μm，43.2 μm]范围内，误差平均值为21.0 μm，标准差为11.8 μm。第2组实验单次预先标定系统参数测量误差分布在[16.1 μm，39.2 μm]范围内，误差平均值为25.2 μm，标准差为8.7 μm；单次同步解算方式测量误差分布在[10.3 μm，28.0 μm]范围内，误差平均值为 19.3 μm，标准差为7.2 μm。第3组实验单次预先标定系统参数测量误差分布在[0.3 μm，36.6 μm]范围内，误差平均值为16.4 μm，标准差为11.2 μm；单次同步解算方式测量误差分布在[1.7 μm，35.8 μm]范围内，误差平均值为16.0 μm，标准差为11.2 μm。

实验表明在单次测量的情况下，两种解算方式能取得相近的测量结果。在Intel Core i5 2.6 GHz计算机配合MATLAB R2016a平台上，预先标定系统参数方式解算耗时0.189 s，同步解算方式耗时6.525 s，解算时间缩短了97.1%，提升了测量效率。当测量点数较少时(测量目标点数i<9)，同步解算方式不能完成解算过程，此时只能采用预先标定系统参数方式解算。

由于单次测量过程中不可避免地存在随机误差，为了减小随机误差对测量结果的影响，实现系统参数的准确标定，对3组实验预先标定的系统参数取算术平均值后作为标定结果，此时解算结果的测量误差与同步解算方式相比有较明显的降低。其中，第1组实验的测量误差分布在[-11.8 μm，16.3 μm]范围内，取模后的误差平均值为6.4 μm，标准差为4.9 μm；第2组实验的测量误差分布在[-24.6 μm，16.3 μm]范围内，取模后的误差平均值为7.9 μm，标准差为6.7 μm；第3组实验的测量误差分布在[-26.0 μm，16.5 μm]范围内，取模后的误差平均值为8.7 μm，标准差为7.6 μm；相较于两种解算方式单次测量误差均值，测量精度依次改善了69.5%、64.6%、46.3%。表明预先准确标定系统参数能有效地抑制单次测量过程中随机误差的影响。

4 实验与结果分析

4.1 坐标测量精度验证实验

图5是坐标测量系统仪器布局图，选用了4台由德国Etalon AG公司生产的LaserTracer，测距不确定度U=0.2 μm+0.3 μm/m。

图5 坐标测量系统仪器布局图Fig.5 Instrument layout of coordinate measurement system

坐标测量精度验证实验利用激光干涉仪和水平导轨进行，如图6所示，在水平导轨的一端放置一台激光干涉仪，并在导轨的气浮运动平台上放置干涉仪反射镜和CER75反射镜靶座，调整CER75反射镜和靶座位置至干涉仪测量光线的延长线上，以减少Abbe误差[11]。

图6 坐标测量精度验证实验Fig.6 Verification experiment of the coordinate measurement accuracy

实验时将反射镜从起始点P0移动到运动平台的第一个点， 相邻测量点间距约500 mm。以激光干涉仪测量的长度值作为距离标准值L0，同时用4台测站测出每个被测点的空间坐标值，计算被测点间距离值L。其中，激光干涉仪测距最大允许误差为±0.4 μm/m，由于导轨长度较短，且实验环境较为稳定，因此激光干涉仪的测距误差予以忽略[12]。

4.2 坐标测量精度验证实验结果分析

采用两种解算方式各进行了3组坐标测量精度验证实验，其结果见表1。表1中，δ1、δ2分别为预先准确标定系统参数方式以及同步解算方式的测量结果L与激光干涉仪标准值L0间的误差。

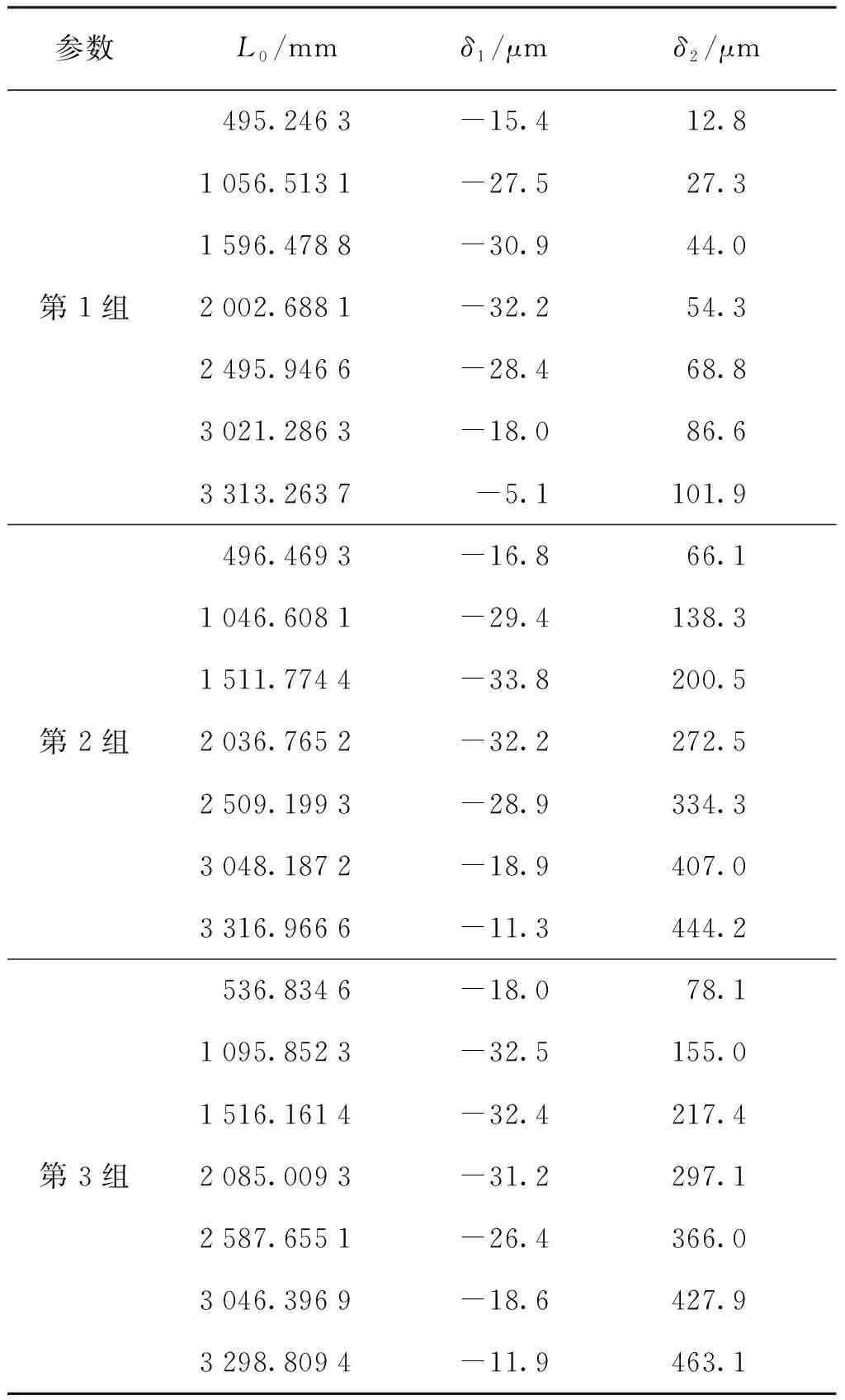
表1 坐标测量精度验证实验结果Tab.1 Results of the verification experiment of coordinate measurement accuracy

3组实验结果中，预先准确标定系统参数方式测量误差与同步解算方式相比有较明显的降低。其中，第1组实验中预先准确标定系统参数方式的测量误差分布在[-32.2 μm，-5.1 μm]范围内，误差平均值为-22.5 μm，标准差为10.0 μm；同步解算方式的测量误差分布在[12.8 μm，101.9 μm]范围内，误差平均值为56.5 μm，标准差为31.7 μm。第2组实验中预先准确标定系统参数方式的测量误差分布在[-33.8 μm，-11.3 μm]范围内，误差平均值为-24.5 μm，标准差为8.7 μm；同步解算方式的测量误差分布在[66.1 μm，444.2 μm]范围内，误差平均值为266.1 μm，标准差为139.6 μm。第3组实验中预先准确标定系统参数方式的测量误差分布在[-32.5 μm，-11.9 μm]范围内，误差平均值为 -24.4 μm，标准差为8.3 μm；同步解算方式的测量误差分布在[78.1 μm，463.1 μm]范围内，误差平均值为286.4 μm，标准差为143.2 μm。

对3组实验结果进行分析可以得出：预先准确标定系统参数方式与同步解算方式相比，测量误差取模后的最大值由463.1 μm降低到33.8 μm；测量误差取模后的平均值由203.0 μm降低至23.8 μm；标准差平均值由104.8 μm降低到9.0 μm。实验证明，采用同步解算方式测量时，测量精度容易受到单次测量过程中随机误差的影响，测量误差分布在[12.8 μm，463.1 μm]范围内；采用预先准确标定系统参数方式后可以抑制随机误差的影响，测量误差分布在[-33.8 μm，-5.1 μm]范围内。

此外，3组实验结果中，同步解算方式的测量误差δ2与距离标准值L0间的相关系数分别为99.6%、100%、99.9%，均为强相关，这表明同步解算方式的测量误差会随距离值的增大而增大；预先准确标定系统参数方式的测量误差δ1与距离标准值L0间的相关系数分别为35.6%、33.8%、43.9%，相关性显著降低，表明预先准确标定系统参数方式抑制了测量误差随距离值的增大的特性，可以有效地改善测量精度。

5 结 论

本文对多边法坐标测量系统中解算方式对测量精度的影响进行了研究。在多边法测量模型基础上，分析了多边法坐标测量系统解算目标点两种方式的区别，并通过对典型的4台测站多边法坐标测量系统的仿真实验，研究了两种解算方式对测量精度的影响，仿真实验结果表明：预先准确标定系统参数对改善系统测量精度具有积极意义，测量精度依次改善了69.5%、64.6%、46.3%。进行了坐标测量精度验证实验，实验结果表明：预先准确标定系统参数能有效抑制单次测量的随机误差，取模后的3组实验平均测量误差相较于同步解算方式，由203.0 μm降至23.8 μm，且测量误差与测量距离的平均相关系数由99.8%降至37.8%，验证了仿真实验结论，对于提升多边法坐标测量系统测量精度具有积极参考意义。