最优炉温曲线与确定其工艺参数问题

李楠，王晓杰，杜咏昊

（东北林业大学，黑龙江哈尔滨市，150000）

1 模型假设与约定

理想情况下回焊炉不同温区温腔内温度能快速准确达到指定值，但由于炉前区域、炉后区域和小温区之间的间隙不做特殊温度控制，其温度以及各温区边界附近的温度也可能收到相邻温区的影响。本问题求解在已设定温区温度下，还需满足制成界限。考虑主要因素，忽略必要影响，建立时间和温度分段进行回归分析和微分方程。

1.1 假设内容

（1）各小温区在题目已定温度下，温腔内温度视为准确、均匀、稳定状态。

（2）忽略一个大温区的各个小温区之间间隙的温度变化。

（3）电路板尺寸很小，其内部温差可忽略，看作温度分布均匀。

（4）电路板的厚度可忽略不计，对电路板采用薄材分析法或集总参数分析法。

（5）在温度变化的情况下，牛顿冷却模型中的比例系数k值[12]相同

1.2 假设可行性

（1）回焊炉各温区均采用强制独立循环，独立控制，上下同时加热的方式，使得各个温腔内的温度均匀、准确，回焊炉启动后，炉内空气温度会在短时间内达到均匀、准确、稳定状态。

（2）由于一个大温区的各个小温区之间间隙长度相对于小温区的长度可忽略，且两个相邻小温区温度相同，间隙温度同时受到两侧小温区的同时传热，间隙温度梯度可近似认为大温区设定温度。

（3）电路板进入回焊炉前具有和室温相同的均匀初始温度。

（4）温度变化差异不是很大的时候，牛顿冷却模型中的比列系数k可以近似认为不变。

2 模型建立

在研究热量传输时，把研究的对象电路板的温度场看成连续的，因此温度的全微分可表示为：

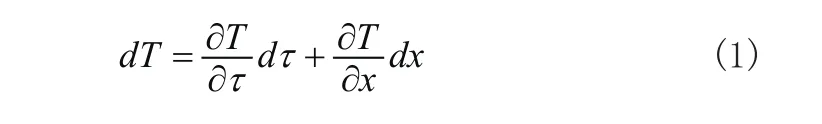
即：

该非稳态导热问题为最简单的一维问题，导热方程为偏微分方程，由于电路板焊接区域中心温度梯度较小，故其非稳态导热过程可用集总参数分析法求解[1]。

为了使每一个节点的热平衡方程具有唯一解，需要附加一定的边界条件和初始条件，统称为定解条件。温度场分析通常有三类边界条件[13]，而本文研究问题是基于回焊炉传热方式为对流传热分析，故主要应为第三类边界条件。

（1）第一类边界条件是指物体边界上的温度函数已知，即：

（2）第二类边界条件是指物体边界上的热流密度q已知，即：

（3）第三类边界条件是指与物体相接触流体介质的温度Tf和换流系数h已知，即：

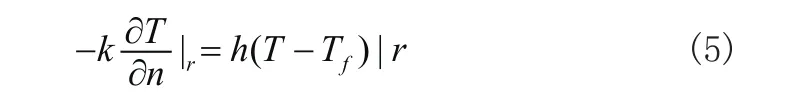
回流焊实际焊接中存在的是第一和第三类边界条件，在本模型中将问题简化——将第一类边界条件转换为第三类边界条件，这样，在仿真过程只考虑转换后的第三类边界条件进行施加载荷[14]。

2.1 牛顿冷却定理

物体在常温下的温度变化可以用牛顿冷却定理来描述：物体温度对时间的变化率与物体温度和它周围介质温度之差成正比。

记物体在时刻t的温度为x=x(t)，它周围介质的温度为A,设A保持不变，则根据牛顿冷却定律建立微分方程模型

其中比例系数k＞0

微分方程满足初始x(t0) =x0的特解为：

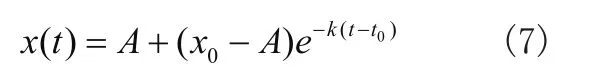
当x0=A时有x(t)=A,即微分方程的常数解，

当x0＞A0时，且A时有x(t)＞A，

当x0＜A时，且A时有x(t)＜A且limx(t)=A

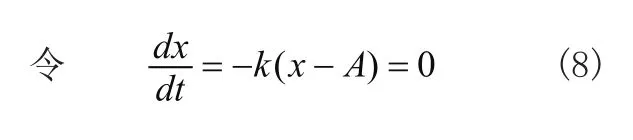
解得x=A,这是微分方程唯一的临界点（即平衡点）。以上分析说明临界点x=A是渐进稳定的。

PCB板不管处于何种焊接状态，皆满足牛顿冷却定律，在同一个温区k值恒定不变，由已知数据可知传送带的过炉速度为70cm/min；温度传感器在焊接区域中心的温度达到300C时开始工作，电路板进入回焊炉开始计时。

2.2 牛顿冷却定理

物体在常温下的温度变化可以用牛顿冷却定理来描述：物体温度对时间的变化率与物体温度和它周围介质温度之差成正比，基于第一问函数结果及其计算方式和牛顿冷却定率可得：

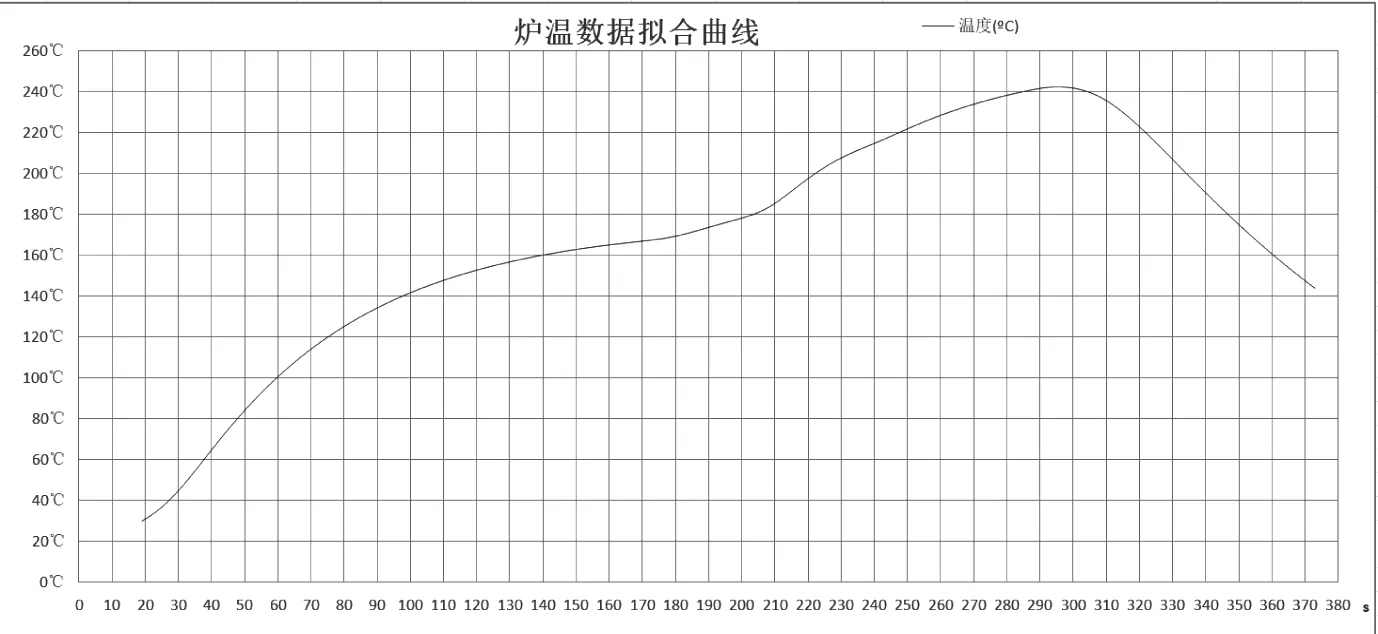
图1 炉温曲线

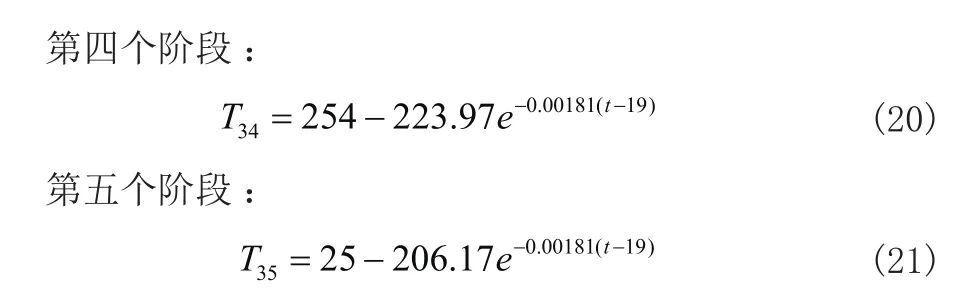
由表1的 制程界限中的第四条限制关系：温度大于217ºC的时间最长为90s，最低为40s。

由5个温区的函数关系式可以初步判断，只有在第三个温区和第四个温区温度才可能达到217ºC，中间有一个峰值,解方程组：