与傅里叶变换有关的线性空间和代数
卫 延, 郑晶晶, 余晶晶, 郭 勇
(北京交通大学 1.全光网与现代通信网教育部重点实验室,2.电子信息工程学院,北京100044)
0 引言
“信号与系统”是电子信息类本科生的专业课程,其教学内涵是研究信号表示和系统描述[1]。傅里叶变换及其性质是课程的核心内容之一,透彻理解傅里叶变换及其性质有利于学生领悟信号表示和频域分析,对于学习拉普拉斯变换和z变换也有帮助[2]。希尔伯特空间和抽象代数[3]的相关数学知识,正是有效的工具,能给本课程的教学带来直观性与深刻性。本文从希尔伯特空间和抽象代数的角度,讨论傅里叶变换的数学内涵以及相关的概念和性质。
1 希尔伯特空间和抽象代数
数域上的线性空间[4]是一个集合,其中的元素满足加法和数乘运算的封闭性,即线性性质。如果线性空间内的任意柯西序列都收敛在该线性空间之内,则称该线性空间是完备的。定义了范数(长度)的完备的线性空间称为巴拿赫空间,定义了内积的巴拿赫空间是希尔伯特空间,希尔伯特中的元素称为向量。

在抽象代数中,群G是带有一种二元运算的非空集合,此二元运算在集合中具有封闭性,满足结合律,且该集合具有单位元,集合中任意元素具有逆元。如果群G中的二元运算还满足交换律,称群G为阿贝尔群。希尔伯特空间显然是一个加法阿贝尔群,加法单位元是零向量。若非空集合R具有两种运算“+”(加)和“·”(乘),集合R关于“+”构成阿贝尔群,关于“·”构成一个幺半群(群中去掉逆元条件),且加法与乘法满足左、右分配律,称R为环[5]。
设R1,R2为环,映射f:R1→R2称为环同态[5],如果f将R1中的幺元(乘法单位元)映射到R2中的幺元,且保持运算:
f(a1+a2)=f(a1)+f(a2)f(a1·a2)=f(a1)·f(a2)
(1)
对所有a1,a2∈R1成立。如果f是双射,称f为环同构映射,此时称环R1和R2是同构的,同构的环具有相同的数学结构。用群、环、同态和同构等概念可以从根本上梳理清楚信号的时域表示和频域表示的关系,说明信号变换、时域分析和频域分析的数学本质。
2 周期信号傅里叶级数与希尔伯特空间
在复数域C上的全体可积函数集合L,在积分意义下,构成希尔伯特空间,称为函数空间。函数空间中的元素是函数g(t),其中自变量t取实数。为研究周期信号,限定所有函数都以T为周期,将此周期函数空间记为LT。为简便,仅研究函数在一个周期上的性质。设周期信号f(t),g(t)∈LT,定义它们的内积为:
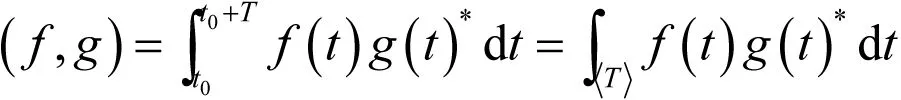
为对连续周期信号进行傅里叶分解,必先指定周期函数空间LT的一组完备正交基函数。虚指数信号集{ejnw0t}(ω0=2π/T,n=0,±1,±2,…)可作为LT的一组完备的正交基函数,

(2)
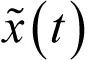
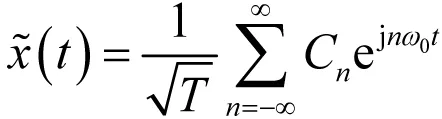
(3)
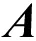

(4)
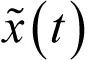
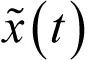

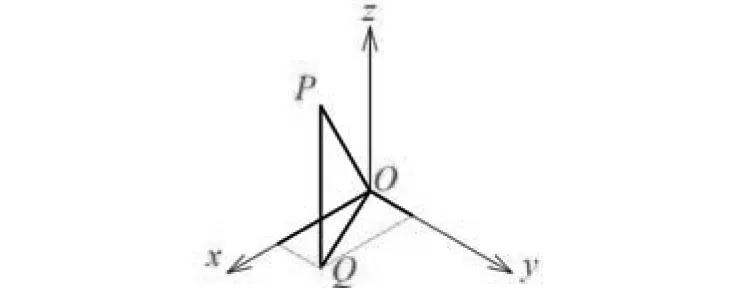
图1 矢量在xOy平面上的最佳近似示意图
3 连续时间非周期信号和傅里叶变换



(5)


(6)
公式(5)(6)是归一化正交基函数下的傅里叶变换与逆变换,与文献[6]一致。

FT(f+g)=FT(f)+FT(g),
FT(f*g)=FT(f)·FT(g)
(7)
此同构映射将(L,+,*)中的零元和幺元,分别映射为(LF,+,·)中的零元和幺元,即:FT(0)=0,FT(δ(t))=1。
类似地,可定义时域函数环(L,+,·)与频域函数环(LF,+,*),根据傅里叶变换的乘积性质可知二者同构:(L,+,·)≃(LF,+,*),如图2(b)所示。同构映射为:
FT(f+g)=FT(f)+FT(g),
FT(f·g)=FT(f)*FT(g)
(8)


(a)(L,+,*)≃(LF,+,·) (b)(L,+,·)≃(LF,+,*)图2 环同构示意图
用希尔伯特空性质和环同构,可直接得出傅里叶变换的一些性质,假定FT[x(t)]=X(jω)。
(1)线性性质:由于信号的时域和频域都是希尔伯特空间,同构映射是一个线性映射,所以对任意的常数α,β∈R,有
FT(αf+βg)=αFT(f)+βFT(g)。
(2)时移特性:
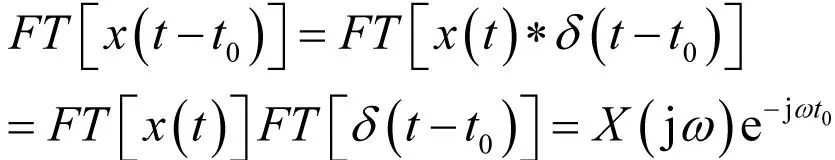
(3)频移特性:
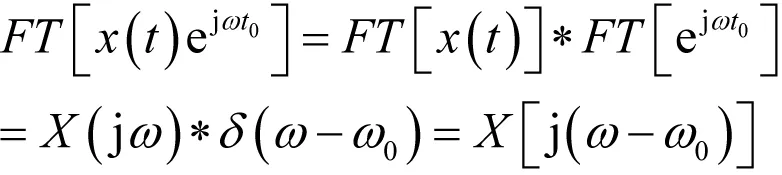
(4)时域微分特性:

(5)积分特性:

(6)频域微分特性:
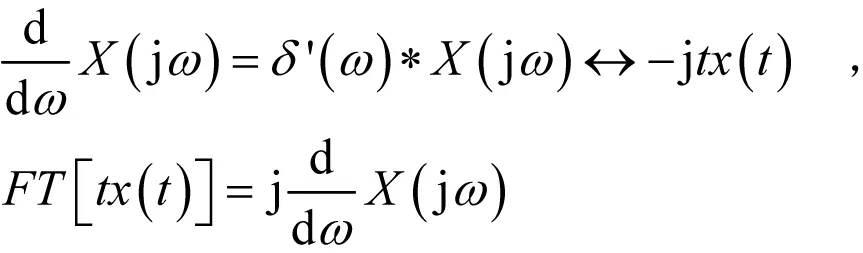
(7)巴塞伐尔定理:在正交归一化基函数下,信号的范数的平方不会改变,即在时域和频域看,信号能量 是不变的,即:

这些公式与“信号与系统”有些常数因子不同,因为本文采用归一化的基函数集,而“信号与系统”中没有使用归一化的基函数集,但是二者在数学本质上是一致的。
4 信号、系统与环同构
在时域函数环(L,+,*)中,线性时不变系统的单位冲击响应为h(t),则连续非周期信号x(t)经过该系统后的响应为y(t)=h(t)*x(t)。傅里叶变换FT作为同构映射,将时域函数环(L,+,*)映射到频域函数环(LF,+,·),相应的,频谱为X(jω)的信号,经过系统函数为H(jω)的系统后,输出信号的频谱为:Y(jω)=H(jω)·X(jω),从而时域分析与频域分析可以精确对应起来,如图3所示。

图3 时域分析、频域分析与环同构示意图
“信号与系统”中的有些问题适合从频域求解,有些问题适合从时域求解,还有一些要综合时域与频域的求解方法。时域和频域之间可任意来回切换,人们不用担心会出错,因为时域和频域是环同构,而同构映射正是傅里叶变换与其逆变换。
5 结语
本文借助希尔伯特空间理论,说明了连续周期信号的傅里叶级数和连续非周期信号的傅里叶变换,本质是信号的正交分解,可用三维欧氏空间的矢量分解来直观理解傅里叶级数、傅里叶变换的几何意义。从抽象代数的观点来看,对于连续非周期信号,时域和频域在整体上是一个环同构,同构映射是傅里叶变换。由希尔伯特空间理论和环同构的性质,可以直接导出连续非周期信号傅里叶变换的一些性质。希尔伯特空间理论和抽象代数的基础知识,也可以用来研究离散信号的傅里叶变换,以及拉普拉斯变换和z变换等的数学本质。正确应用这样的数学工具,能给“信号与系统”的教学带来直观性和深刻性,并且提高学生对课程内容的认知水平以及应用数学工具的能力。

