基于二分迭代法的三心圆复曲线优化算法及程序设计

熊江陵 曾凡云 唐俊成 韩 扬

(中国电建集团中南勘测设计研究院有限公司 长沙 410014)

在传统的公路及城市道路设计中，通常将平面交叉口右转弯车道边线简化为单圆曲线形式，一方面是为了便于施工，另一方面原因是双心圆及三心圆等复曲线无法通过固定的公式进行直接计算。但是在高等级公路及渠化城市道路设计中，将交叉口右转弯车道边线设计为双心圆或三心圆复曲线具有一定的必要性，因为它能有效提高右转弯通行能力和行车舒适性。蔡伟等[1]研究了不同类型弯道路缘石对车辆在交叉口转弯处行驶速度和轨迹的影响，结果表明在交叉口弯道处采用三心圆曲线进行布设，不但节约用地资源，也有利于提高车辆在交叉口转弯处行车的舒适性。JTG D20-2017《公路路线设计规范》[2]在10.4.3条规定：渠化平面交叉的右转弯车道，在内侧路面边缘应采用三心圆复曲线。文献[3]指出以铰接列车控制设计时，相交路面的边缘应采用复曲线。在三心圆复曲线的计算方法方面，相关研究较少，朱家兵等[4]根据相交道路线形，分左直右直、左直右曲、左曲右直、左曲右曲等情况，提出一种以切线长度为逼近目标的三心圆复曲线计算方法，但该方法在曲线相交的交叉口中计算误差较大(1 m)，并且文献中没有对进、出口道均为曲线的形式进行详细论证。

为研究三心圆复曲线的通用计算方法，基于三心圆复曲线终点坐标计算公式，提出以终点距离为逼近目标的二分迭代法，并对该方法收敛性和迭代初始值区间选取进行论证。通过在实际项目中的应用结果表明：该算法能正确求解任意线形相交的交叉口右转弯车道三心圆复曲线，具有更好的通用性、稳定性和求解精度，同时也具有较高计算效率。

1 三心圆复曲线切线长公式及应用

根据文献[5]中介绍的方法，进、出口道为直线时，左、右侧切线长Tq、Th分别为

Tq=(R1-R2)sinα+[R3-(R3-R2) cosγ]/

sinδ-[R1-(R1-R2)cosα]/tanδ

(1)

Th=(R3-R2)sinγ+[R1-(R1-R2) cosα]/

sinδ-[R3-(R3-R2)cosγ]/tanδ

(2)

式中：R1、R2、R3分别为3段圆弧的半径，R2小于R1、R3；α、β、γ分别为3段圆弧对应的转角；δ为三段圆弧旋转角度之和，各参数示意图见图1。

图1 三心圆复曲线切线长公式参数示意图

假定3段圆弧长度分别为L1、L2、L3，则有公式

α=(L1/R1)·(180°/π)

(3)

β=(L2/R2)·(180°/π)

(4)

γ=(L3/R3)·(180°/π)

(5)

δ=α+β+γ

(6)

通过确定R1、R2、R3，并且确定3段圆弧中任意2段的长度，或选择3段圆弧相等，利用式(1)～(6)可求出Tq和Th，进而可以计算出A、D的位置和确定3段圆弧的准确位置。

当进、出口道为曲线时，文献[4]以切线长T值为目标进行迭代逼近，目标控制条件为Th-Th′<10-10，其中Th为根据公式(2)计算得到的切线长，Th′为迭代点处实际的切线长。经测试，该方法结果存在较大误差，原因是路线的圆弧半径较大，δ的微小变化对Th结果影响较小，但对Th′影响较明显。

2 基于终点距离逼近的二分迭代法

为解决上述三心圆复曲线计算的误差问题，并考虑相交道路线形的任意性，提出以终点距离为逼近目标的二分迭代法。

由于相交道路几何条件的不确定性，对于曲线相交的交叉口，三心圆复曲线仅在某一范围存在可能解，可以视为局部收敛的非线性问题[6]。局部收敛非线性问题求解，需要解决如下3个问题。

1) 选择合适的迭代公式。

2) 选择合适的迭代初始值。

3) 保证迭代的收敛性。

2.1 选择迭代公式：基于终点距离逼近的迭代方程

当相交道路线形为曲线时(见图2)，三心圆复曲线终点切向量及坐标计算公式如下。

图2 三心圆复曲线终点切向量及坐标计算参数示意图

Ve=R(Vs,δ)

(7)

Pe=Ps+R1·(υ1+υ1′)+

R2·(υ2+υ2′)+R3·(υ3+υ3′)

(8)

式中：Ve为复曲线终点向量；Vs为起点向量；R(Vs,δ)为将向量Vs顺时针旋转δ角度；Pe为复曲线终点坐标；Ps为复曲线起点坐标；υ1、υ2、υ3分别为3段圆弧起点处指向圆心的单元向量，υ1′、υ2′、υ3′分别为3段圆弧终点处背向圆心的单位向量。

三心圆复曲线在终点需与边线相切，即应满足如下2个条件。

1) 复曲线终点切向量与终点在边线上投影处的切向量相等。

2) 复曲线终点与终点在边线上投影点距离为0。

用公式表示为

D(Ve,Ve′)≤ε

(9)

D(Pe,Pe′)≤ε

(10)

以式(10)为逼近目标建立二分法迭代方程，其中式(10)应以满足式(9)为前提，他们的因变量分别为起点切向量Vs和Ps起点坐标。

2.2 选择迭代初始值区间

对于迭代方程为y=f(x)的二分迭代法，需要确定迭代求解的初始值区间[X1,X2]，保证[X1,X2]对应的目标值y1，y2满足y1×y2≤0。对于式(9)，假设复曲线终点向量目标解为Ve*，则初始值区间[Vs1,Vs2]应满足复曲线终点向量Ve1、Ve2分别在Ve*的两侧。对于式(10)，初始值区间[Ps1,Ps2]应满足复曲线终点坐标Pe1、Pe2分别在出口车道边线的两侧。

由于路线几何的不确定性，可能收敛区间[Ps1,Ps2]仅存在于路线中很短的一段距离，为了快速、准确地找出初始值区间[Ps1,Ps2]，参考文献[4]，可以先利用式(1)、(2)以切线长为逼近目标迭代求解到复曲线起点Ps，然后再在Ps附近找出符合上述条件的[Ps1,Ps2]，此处不再赘述。

2.3 迭代收敛性论证

迭代方程为y=f(x)在区间[X1,X2]能否收敛，除需要满足对应的目标值y1×y2≤0外，还应满足y=f(x)在区间[X1,X2]连续。

根据式(3)～(8)，可以得到

Pe=Ps+f(Vs,δ)

(11)

当三心圆复曲线起点Ps确定时，Vs能唯一确定，而δ的大小也与起点位置有关，也就是说Pe可以表示为

Pe=F(Ps)

(12)

为保证行车的顺畅性，路线在几何上也必然是连续且光滑的，也就是说Ps是连续变化的，所以基于终点距离逼近的迭代方程D(Pe,Pe′)≤i也具备连续性。

分别对相交道路为直-圆、圆-直、圆-圆等情况进行测试，终点距离D(Pe,Pe′)值迭代收敛过程图见图3。

图3 二分法迭代计算收敛过程图

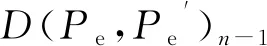
3 以终点距离逼近为目标的二分法迭代计算流程图

根据上述分析，以终点距离逼近为目标的二分迭代法需要如下过程。

1) 根据切线长预估复曲线起点位置。

2) 在预估的起点附近确定迭代区间初始值。

3) 以终点距离逼近为目标进行二分迭代计算。

算法流程图设计见图4。

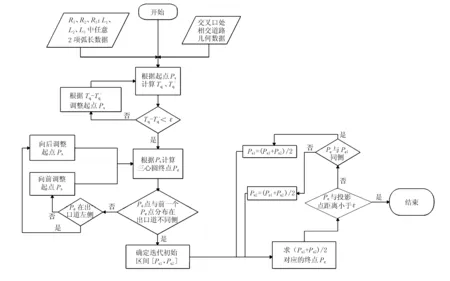
图4 三心圆复曲线终点逼近二分迭代法计算流程图

其中三心圆复曲线终点切向量迭代逼近的算法包含在“根据Ps计算三心圆终点Pe”这一步骤中，迭代步骤与计算Pe相同，不再赘述。

4 项目应用

金山大道位于广西省河池市，设计长度2 350 m，双向八车道，设计速度60 km/h，为城市主干路。其中金山大道与开元大道相交的交叉口位于K1+062.705处，相交处道路主线段为半径625m的圆弧，支线段为直线，最小交角约为78°，该右转区间行车道边线选择三心圆复曲线，R1、R2、R3分别为25,15,25 m，3段圆弧长度相等。

基于上述三心圆复曲线算法，利用三维道路软件OpenRoads Designer进行二次开发，完成“交叉口右转边线”设计功能。经测试，该功能可以正确生成该交叉口右转弯车道三心圆复曲线，边线图见图5，三维实体模型图见图6。

图5 交叉口右转弯车道边线图

图6 交叉口三维实体模型图

5 结语

1) 利用以终点距离逼近为目标的二分迭代法，计算三心圆复曲线，计算结果精度高，能够将复曲线起、终点误差控制在10-8m以内。

2) 该算法具有通用性，能够应用于进、出口车道为直-直、直-曲、曲-直、曲-曲等不同情形。

3) 该算法在进、出口车道足够长的前提下，能保证收敛性，并且迭代计算效率较高。

3) 仅通过修改迭代目标公式，该算法框架可扩展应用于双心圆复曲线的计算。

4) 该算法在逼近方法、初始值选取、收敛性论证等方面，对道路路线中复杂复曲线计算有一定参考价值。