两款水泥混凝土路面结构有限元分析软件接缝模拟技术比较*

武琨璐 蒋 鑫 古含焱 Babiker Lana Elabbas Abdelhaliem 付用国 邱延峻

(1.西南交通大学土木工程学院 成都 610031； 2.西南交通大学道路工程四川省重点实验室 成都 610031；3. 西南交通大学高速铁路线路工程教育部重点实验室 成都 610031)

水泥混凝土路面结构所出现的唧泥、碎裂、错台和角隅断裂等损害多与接缝密切相关[1]，接缝工作状况严重制约着路面结构的使用性能。为了控制路面因温缩应力和翘曲应力所引起的开裂，水泥混凝土路面面层在横、纵2个方向设置接缝，通过集料嵌锁或设置传力杆和拉杆来传递部分荷载。路面接缝布置见图1。

图1 路面接缝布置示意

为深入研究接缝的传荷效果，涌现出诸多有限元软件可对接缝进行模拟，其中方法之一是直接视传力杆、拉杆等为梁、杆等结构性单元，如ILLI-SLAB和JSLAB。将传力杆看作二维梁单元，EverFE[1-2]中的传力杆则由支承在混凝土弹性基础上的剪切梁和弯曲梁共同模拟。对传力杆予以细致建模虽可提高计算精度，但在有限元软件中的实现和用户操作方面等存在较大难度。若采用线性弹簧模型，认为接缝间传递的剪切力等于接缝两侧的挠度差与剪切弹簧常数的乘积，则更具实用性，可与接缝传荷能力建立唯一对应关系。基于此法所开发的2D程序KENSLABS[3]、3D程序FEAFAA[4]各有特色，已得到广泛应用，然而关于它们的接缝模拟技术的详细讨论尚鲜见报道。

本文拟针对内嵌于KENSLABS、FEAFAA这两款程序的水泥混凝土路面结构接缝模拟技术开展横向比较，通过具体算例，讨论二者计算结果的差异及原因，有助于水泥混凝土路面结构分析工具的科学选用。

1 线性弹簧模型模拟接缝的基本原理

KENSLABS、FEAFAA均将接缝刚度与板和地基的刚度矩阵组合为路面结构的整体刚度矩阵，将外部作用的荷载转换为节点力向量，即可通过求解方程(1)得到节点位移。

Kδ=F

(1)

式中：K为整体刚度矩阵；δ为节点位移；F为外部作用的节点力。

由上所述，在考虑利用有限元法模拟接缝时，核心工作在于求解接缝刚度。线性弹簧模型见图2，相邻板块接缝两侧对应节点之间看作由线性弹簧相连。当受到外部荷载作用时，节点能够承受竖向剪切力或弯矩作用。软件通过确定接缝刚度的数值，使模型中节点弹簧常数与实际接缝刚度相同。

图2 线性弹簧模型

其中KENSLABS在模拟集料嵌锁型接缝时，接缝刚度由剪切弹簧常数和力矩弹簧常数表示；模拟传力杆型接缝时由剪切弹簧常数表示[5]。而FEAFAA则默认为接缝仅传递竖向剪切力。剪切弹簧常数、弯矩弹簧常数的具体含义如下。

剪切弹簧常数Cw的计算式为

(2)

wd=wl-wr

(3)

式中：Fw为沿接缝处单位长度上的剪力；wd为接缝两板之间的挠度差；wl为受荷板挠度值;wr为非受荷板挠度值。

弯矩弹簧常数Cθ的计算式为

(4)

式中：M为沿接缝处单位长度上的力矩；wθ为接缝两板之间的转角差。

计算接缝刚度的重点是确定沿接缝节点上弹簧常数的数值。接缝刚度受缝隙宽度、集料啮合程度和断面形状等因素的影响，很多因素难以量化[6]。当缝隙宽度不大于3 mm时，多视为集料嵌锁型接缝，此时弹簧常数由用户自定义输入，一般情况下在(0.5～4.0)×104MN/m3的范围内取值。

而对于传力杆型接缝剪切弹簧常数的确定，两款软件方法有所不同，下面分别详细阐述。

1.1 KENSLABS接缝刚度计算

对于KENSLABS软件，由于接缝中剪力作用导致两板产生的挠度差wd由传力杆自身的剪切变形ΔS和传力杆作用下混凝土产生的变形y0共同组成，变形图见图3，可知它们之间的关系为

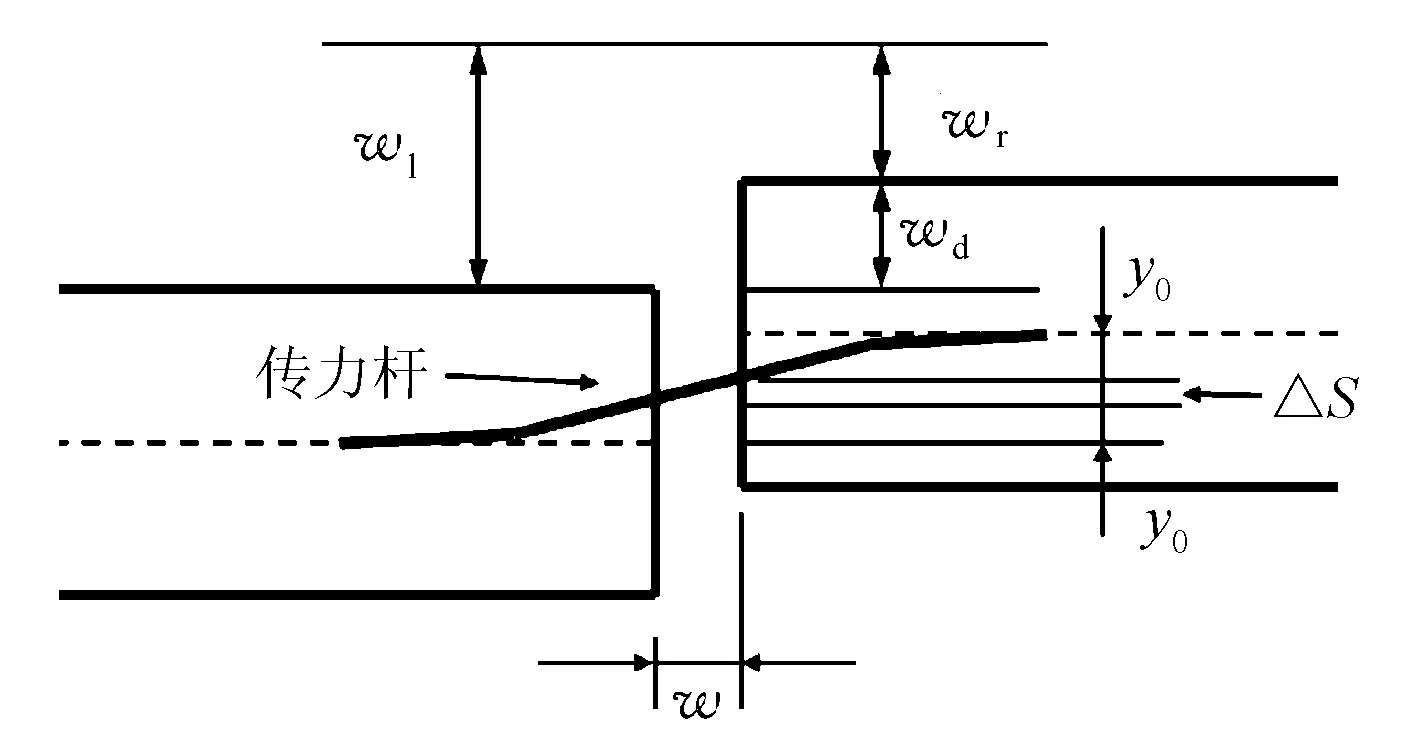
图3 KENSLABS中传力杆的剪切变形

wd=2y0+ΔS

(5)

接缝传递的剪切力Fw集中作用在沿接缝的节点上，L为沿接缝节点的平均间距，则可以得到

Fw=LCwwd

(6)

传力杆的松动可通过传力杆和混凝土之间的间隙wg予以考虑。若有间隙存在，则式(6)变为

Fw=LCw(wd-wg)

(7)

若传力杆的平均间距为s, 则每个节点处传力杆的数量为L/s，每根传力杆上的剪力P为

(8)

传力杆的剪切变形ΔS和传力杆作用下混凝土的变形y0可以由式(9)和(12)计算得到。

(9)

(10)

(11)

(12)

式中：w为接缝宽度；G为传力杆的剪切模量；γd为传力杆的泊松比；A为传力杆截面积；Ed、Id分别为传力杆的弹性模量和截面惯性矩；β为混凝土与杆的相对刚度；K为混凝土对传力杆的支承模量；d为传力杆的直径。

联立以式(5)、(8)、(9)、(11)并与式(6)比较可得传力杆接缝剪切弹簧常数Cw的计算公式为

(13)

1.2 FEAFAA接缝刚度计算

对于FEAFAA软件，传力杆接缝的传荷作用由传力杆截面的抗剪刚度和混凝土对传力杆的承压刚度组合而成。计算过程如下。

混凝土对传力杆支承的剪切弹簧刚度DCI为

(14)

式中：β为混凝土与传力杆的相对刚度，可由式(12)求出。

传力杆自身的剪切弹簧刚度C为

(15)

(16)

式中：Az为传力杆等效截面面积，取值为0.9A。

可得传力杆组合剪切刚度为

(17)

式(17)分母第一项中的系数2表示同时考虑了受荷板和非受荷板对传力杆的支承而产生的变形。

联立式(14)～(17)得到单位长度上的剪切弹簧刚度的计算式为

(18)

2 两款软件模拟接缝实施技术

基于上述基本原理，下面详细阐述这两款软件模拟接缝的具体实施技术。

2.1 面板分割

接缝传荷效果在多块板体系中方才涉及。KENSLABS最多可将面板结构划分为9个板块。通过“General”选项栏中的“NSLAB”设定板块数量后，对板块进行编号。每个板块可有不同的尺寸，但相邻的板宽度必须相同。划分完成后对板块单独进行编号。

FEAFAA只能设置特定数量的板块(1、2、4、6、9)，每个板块具有相同的尺寸，无需进行编号。

2.2 接缝位置确定

KENSLABS通过“General”选项栏中的“NJOINT”中设定接缝数量，最多为12条。对每条接缝编号后，通过参数JONO(J,I)来确定接缝位置。其中第一个下标J(1,2,3,4)表示板的四边(左、右、下和上)，第二个下标I表示板块的编号。具体通过KENSLABS中“Slab”选项栏中点击“Arrangement”，进行参数输入。

FEAFAA通过勾选“Joint Modeling”栏中的“X-Direction Dowel Bar”或“Y-Direction Dowel Bar”选项，分别设置面板系统中的纵缝或横缝。

2.3 接缝刚度确定

KENSLABS中每条接缝的刚度都可以在“Joint”项目栏中单独设置。对于集料嵌锁型接缝，输入参数“SPCON1”和“SPCON2”，分别代表剪切弹簧常数Cw和弯矩弹簧常数Cθ，其余参数值为0。对于传力杆型接缝，输入参数“SCKV”“BD”“BS”“WJ”“GDC”“NNAJ”，分别表示混凝土对传力杆的支承模量K、传力杆的直径d、平均间距s、接缝宽度w、传力杆和混凝土之间的间隙wg、该接缝上的节点数N。若传力杆等间距分布，“NNAJ”的值为0。否则输入“NNAJ”确定接缝上节点数目后，双击数值框后输入参数“BARNO”，代表沿该接缝每个节点上分布的传力杆数目。传力杆自身的材料性质，包括弹性模量Ed和泊松比γd分别在“Optional”选项栏“Dowel”中的“YMSB”和“PRSB”中设置，输入界面见图4。

图4 KENSLABS中计算参数输入界面

FEAFAA中每条接缝只能同时设置相同的接缝刚度。依次输入传力杆直径d、间距s和接缝宽度w。输入界面见图5。

图5 FEAFAA中计算参数输入界面

混凝土对传力杆的支承模量K有2个默认值，通过在“Method of Dowel Bar Placement(传力杆的放置方式)”中进行选择。勾选“Bar placed in fresh concrete(置于现浇混凝土中)”时，K=57 159.55 MPa(8 290 000 psi)；勾选“Bar placed in drilled holes(置于钻孔中)”时，K=36 336.65 MPa(5 270 000 psi)。默认传力杆的泊松比γd、弹性模量Ed分别为0.3、200 000 MPa(29 000 000 psi)。

2.4 模型计算求解

KENSLABS在运行过程中，根据总刚度矩阵维度是否小于70 000，分别采用高斯消去法、迭代法联立求解方程式(1)。

FEAFAA首先调用INGRID程序划分模型网格，生成输入文件。之后调用计算引擎NIKE3D程序，使用迭代法和插值法计算出各个节点的位移和应力，以文本格式输出。最后使用NIKEPLOT程序处理输出数据，便于TecPlot软件对其可视化。

2.5 接缝相关的计算结果后处理

KENSLABS中将计算结果输出在.txt文件中。包括沿接缝上每个节点的剪力(FAJ1)和弯矩(FAJ2)、每根传力杆上的剪力(FAJPD)、混凝土对传力杆的支承应力(BEARS)和传力杆的剪切应力(SHEARS)等，计算结果见图6，可通过ORIGIN、SURFER等第三方软件可视化。

图6 KENSLABS接缝相关计算结果

FEAFAA将输入数据和计算结果存放在n3dhsp文件中，计算结果见图7。

图7 FEAFAA接缝相关计算结果

然后调用NIKEPLOT程序，读取n3dhsp文件并生成model_load.dat 和model_stress_1.dat。前者包含三维模型的几何数据、荷载和边界条件。后者包含单元节点坐标，以及外推到节点的6个应力分量、应力不变量和节点温度。二者以特定的数据格式输出，可通过TecPlot程序进行可视化。

3 算例分析与讨论

3.1 问题描述

取设有横缝的2块板体系为研究对象。每块板的长度、宽度和厚度分别为4，4，0.26 m。各结构层主要计算参数见表1。假设面层与水泥稳定基层之间光滑无摩阻，基层与地基之间为完全接触。暂不考虑温度翘曲和初始间隙的影响。

表1 各结构层主要计算参数

3.2 有限元模型建立

荷载系轴重100 kN的单轴双轮组，轮胎接触压力为0.7 MPa[8]，作用范围为18.9 cm×18.9 cm，两侧轮隙间距为190 cm。因板角破坏的情况最为常见，故将荷载作用在板角处[9]。接缝为宽度0.2 cm的胀缝，传力杆直径3.2 cm，等间距20 cm排布，传力杆对混凝土的支承模量为57 172 MPa。假定传力杆与混凝土之间无间隙。不考虑纵缝处拉杆的影响。

KENSLABS有限元模型见图8。

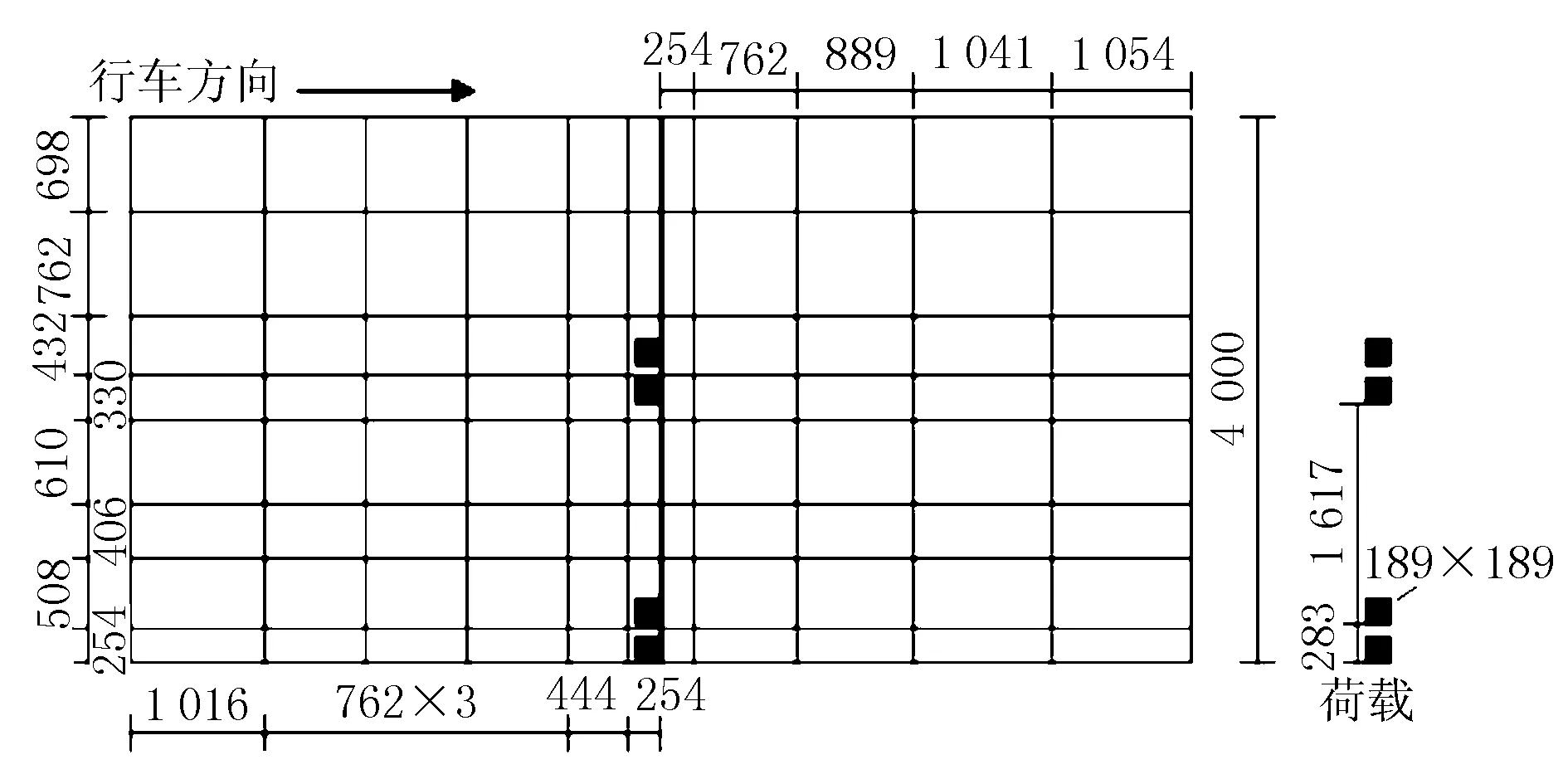
图8 KENSLABS路面结构有限元模型(单位：mm)

整个模型共划分为88个单元、117个节点，满足软件的计算规模限制要求。单元最大长宽比为1 016/330=3.1<5，符合软件精度要求。为了提高计算精度，荷载作用处网格划分较密。

FEAFAA则采用非协调性八节点六面体砖单元进行建模，有限元模型见图9。2个板块、基层和地基的网格划分均为35×35。地基使用无限单元进行模拟，划分基层和地基网格时将每个单元边长控制在12 in(304.8 mm)左右。

图9 FEAFAA路面结构有限元模型(单位：mm)

3.3 计算结果分析

两款软件计算得到的板底应力分布结果比较见图10。

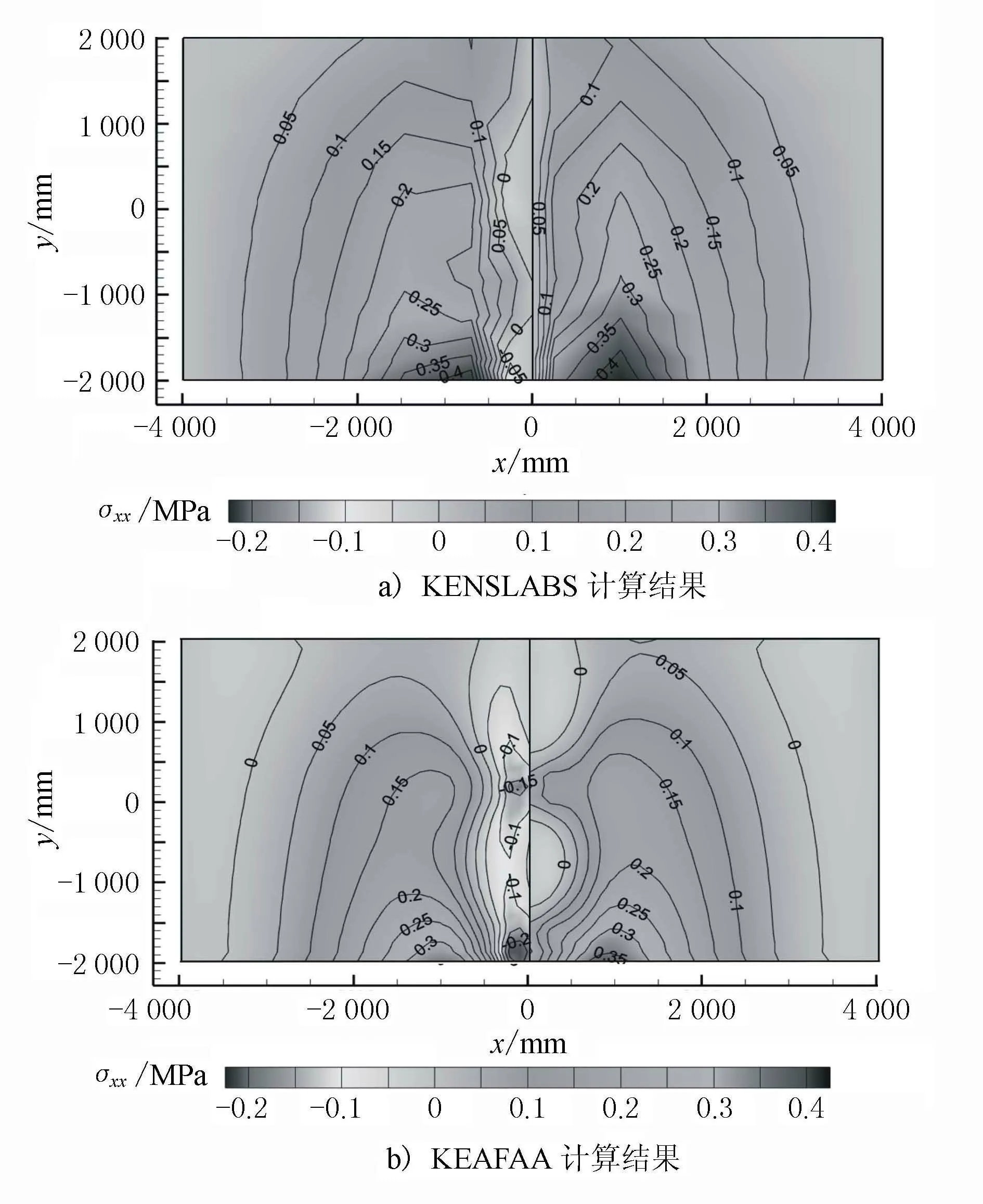
图10 面板底部主应力分布图

由图10可知，在荷载、路面结构参数相同的情况下，两款软件的计算结果宏观规律保持一致。轮载下方板底受到压应力，随着与轮载中心距离的增大，面层底径向应力由压应力调整为拉应力。非受荷板中的最大拉应力大于受荷板中的最大拉应力。FEAFAA计算得到的板底最大压应力较大，而最大拉应力较小。

路表弯沉的空间分布情况见图11。图11表明二者亦相似。采用以挠度比表征的传荷系数LTE来评价接缝传荷能力，计算结果见表2。KENSLABS和FEAFAA计算得到的传荷系数分别为93.1%，97.2%。

图11 路表弯沉的空间分布

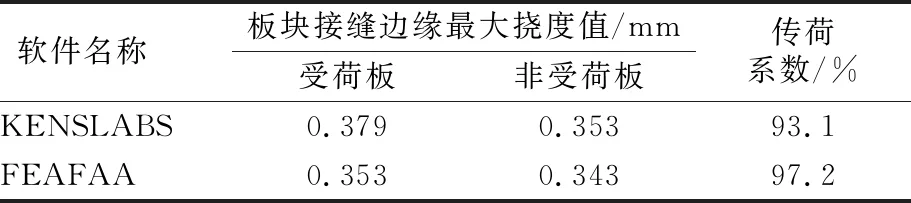
表2 板块接缝边缘最大挠度值及接缝传荷系数

两款软件接缝模拟技术不同导致计算结果产生差异，体现在以下两方面。

1) 对比式(13)、式(18)，KENSLABS未考虑传力杆接缝间隙部分对抗弯刚度的贡献，剪切弹簧刚度计算值小于FEAFAA。对于缝隙宽度较小的传力杆接缝来说，该影响可忽略不计。

2) 网格划分对计算结果的收敛性和精度影响甚大[10]。在板块沿接缝两侧进行节点排布时，KENSLABS受半带宽的限制，靠近荷载周围节点紧密排布，远离荷载区域则比较稀疏；FEAFAA则可以划分大量等距离节点，适当提高了精确度。

4 结论

1) 模拟缝隙宽度较大的传力杆型接缝，或为提高计算精度，网格划分细密时，总刚度矩阵维度较大，使用FEAFAA将体现出一定的优越性。

2) 若不同位置接缝中传力杆自身的弹性性能参数与常规数值不同或不等间距分布时，宜采用KENSLABS。

3) KENSLABS的结果数据量较少，易于用多种第三方软件对结果进行可视化处理。FEAFAA的结果数据量较多，虽易被TecPlot读取处理，但要求用户熟悉TecPlot软件，若要使用其他第三方软件处理则要求用户重新编排数据格式，稍为繁琐。