时差法超声波流量计在大型渠道的应用分析

陈兴农 ，李 仪 ，胡天忠 ，张 伟 ，汤黎明 ,

（1. 长江水利委员会水文局汉江水文水资源勘测局，湖北 襄阳 441000；2. 南水北调中线干线工程建设管理局陶岔管理处，河南 南阳 474450）

南水北调中线调水主干渠（以下简称干渠）陶岔渠首（以下简称渠首）位于河南省淅川县陶岔村，渠首下游渠道设计最大输水流量为 420 m3/s，设计标准输水流量为 350 m3/s，属于大型调水渠道。渠首出水口下游渠道约 300 m 处为弯道，3 000 m 处有分水口。弯道、分水口对渠道内水力要素影响较大，渠首出水口下游 400～2 500 m 内渠道顺直，剖面呈梯形，底部宽度为 13 m，两边坡比均为 1∶3。渠道内水力要素复杂，采用传统流量测验方式测流无法满足流量实时精准监测需求，为确保干渠渠首段流量监测的连续性、精准性，经勘察论证，选取陶岔出水口下游水力学条件较优的 1 400 m 处渠段，安装 Quantum 时差法超声波流量实时监测系统作为流量精准监测设施，进行调水总量监测。选用该系统既可满足流量实时监测需求，又可满足复杂水力要素下流量精准测量，保证调水总量数据的可靠性。

1 时差法超声波流量计测量基本原理

时差法超声波流量计是 Quantum 时差法超声波流量实时监测系统的重要组成部分。工作时首先测量横跨断面的 1 个或几个水层的平均流速，然后利用这些水层平均流速与断面平均流速建立关系，求出断面平均流速，再通过断面平均流速与该水位下断面面积的乘积求出断面的流量。时差法超声波测量水层平均流速原理如下：超声波在流体中顺流和逆流传播相同距离时存在时间差（传播历时差异），传播历时差异与被测流体的流动速度有关，传播历时可以通过技术手段监听[1-2]。利用测得的传播历时差异，通过模型公式可计算出断面的平均流速。

1.1 单层流速的测量

时差法超声波流量计测量流速示意图如图 1 所示，如果t1是超声波从换能器 1 到换能器 2（顺流）的传输时间，t2是超声波从换能器 2 到换能器 1（逆流）的传输时间，则从换能器 1 到换能器 2 的历时为

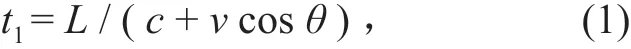
从换能器 2 到换能器 1 的历时为

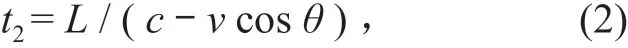
式中：v为河流某水层平均流速；L为换能器 1 和2 之间的距离；θ为声波传输路径与水流方向的夹角；c为特定水温下，超声波在该水环境下的传播速度。

根据式 (1) 和 (2)，监听时差 Δt计算如下：

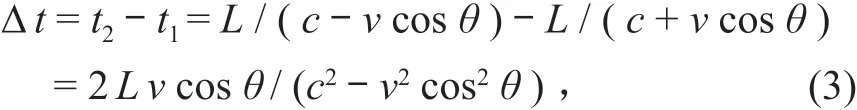
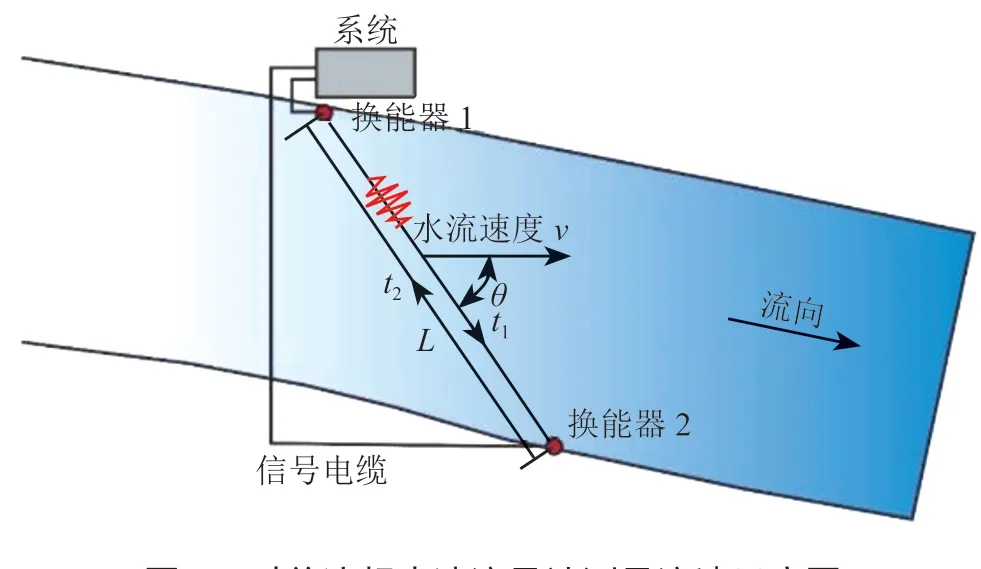
图 1 时差法超声波流量计测量流速示意图

则流速v为

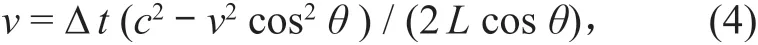
由于v2cos2θ＜＜c，舍弃v2cos2θ后，换能器 1到 2 水层的平均流速公式约为

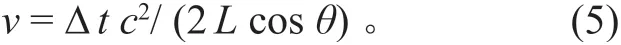
1.2 断面平均流速的率定

断面流量Q由断面面积A和平均流速vm计算得到，计算公式为Q=A·vm。

采用时差法超声波流量计测得的水层平均流速v与断面平均流速vm间存在vm=Kv的关系（K为率定系数），示意图如图 2 所示。

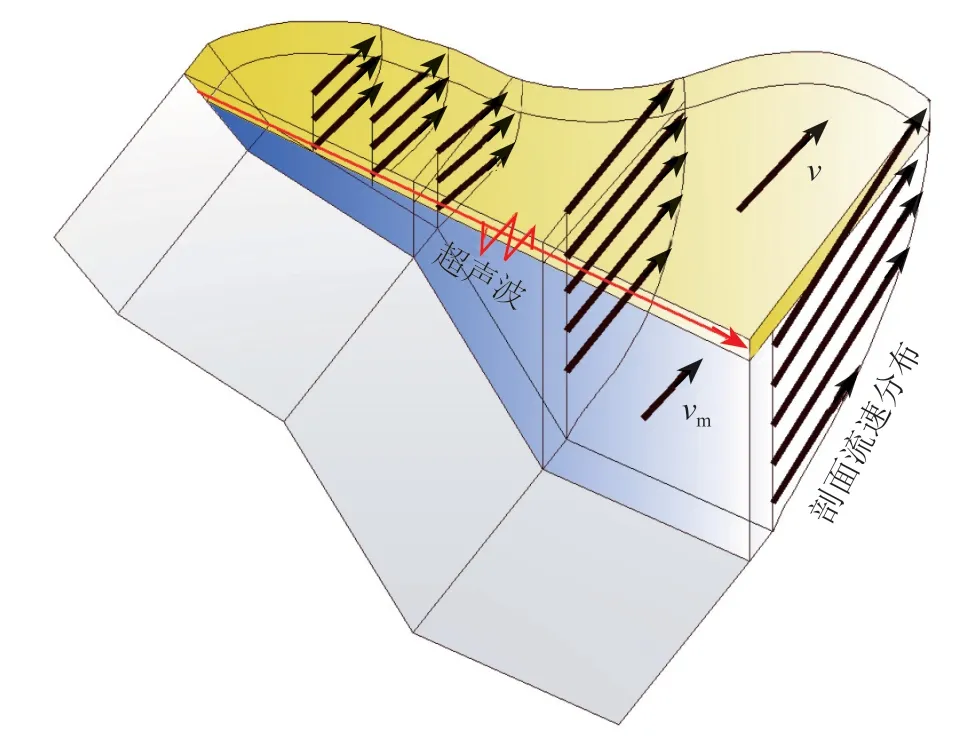
图 2 断面平均流速 vm 与水层平均流速 v 关系示意图

率定系数K可以通过理论推导，数学模型计算，或其他测量方式测量计算。为区分理论速度系数k1与特定测量装置的校准系数k2，Quantum 时差法超声波流量实时监测系统在率定系数K的计算模型上采用如下公式[3]：

因此，时差法超声波流量计断面流量计算公式为

国际标准 ISO 6416 推荐的k1值与换能器安装高度H和水深h的比值相关，具体如表 1 所示[4]。

表 1 国际标准 ISO 6416 推荐的 k1 值

k2的确定，对于时差法超声波流量计是极为关键的。所选断面的水流理论流速受水位、流向、断面轮廓等一些因素的影响，因而在测量中发现理论速度系数k1的特定偏差可通过特定测量装置的校准系数k2进行修正。由于k2=f(A，Q)，而A和水位Z的关系为A=f(Z)，Q和影响流量的水力因素φ的关系为Q=f(φ)，从而得到k2=f(Z，φ)，由于干渠渠道为人工规整渠道，各水力要素相对稳定，因此忽略φ影响因素，可将k2的计算公式进一步简化为k2=f(Z) 。

在实际应用中，需要随着水位变化动态调整k2值，以保证时差法超声波流量计所测得数据的准确性。在 Quantum 时差法超声波流量实时监测系统运行比测期间，选择不同水位、流量级，采用转子式流速仪或走航式 ADCP 进行现场比测，得到k2与水位Z的关系，如表 2 所示 。

表 2 特定测量装置的校准系数 k2 值

1.3 分层流量的测量

当测验断面水位变幅大，受回水影响，断面形状不规则，垂线流速分布与理论分布差异较大，流量测验精度要求较高时，可将水深划分成不同的水层，每层水深处安装 1 对换能器，测得各层的平均流速，进而提高流量测验的精度[5]。

陶岔主干渠安装的时差法超声波流量计采用4 层测量系统，安装 4 对换能器的分层测流示意图如图 3 所示。在测得断面各水层平均流速后，乘以对应的河宽，得到单深流量，以水深为纵坐标，单深流量为横坐标，绘制垂直流量分布曲线图，用求积仪量出垂直流量分布曲线与纵坐标所包围的面积，即为全断面的流量。全断面流量也可用下式计算：

式中：α为河底流速系数，可由试验确定，无试验资料取 0.8；B0，Bi分别为河底和第i个换能器对应的宽度；vi为第i个换能器测得的平均流速；ΔHi为第i个换能器至第（i-1）个换能器（或河底）的水层深度；ΔHn+1为第n个换能器（最上 1 个）至水面的水层深度；n为换能器个数。

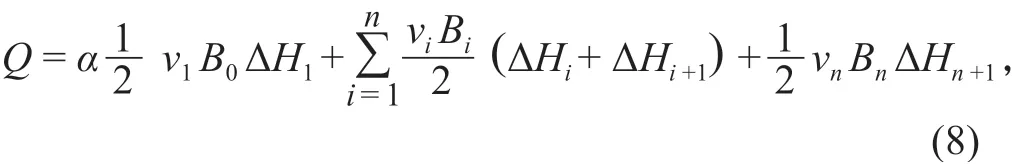
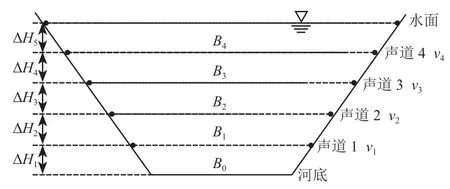
图 3 分层测流示意图

2 时差法超声波流量计的安装

2.1 换能器安装位置

为提高测量精确度，陶岔主干渠时差法超声波流量计采用 4 层换能器分层测流，且换能器和超声波传输的路径都与渠道呈 45° 夹角，依据断面资料，按渠道最大水深 10 m 设计，从河底至上方高度分别为 1.20，2.90，4.60，6.30 m 处安装 4 层换能器，安装示意图如图 4 所示。图中：1.1 和 1.2 为第 1 层换能器安装位置，2.1 和 2.2 为第 2 层换能器安装位置，3.1 和 3.2 为第 3 层换能器安装位置，4.1和 4.2 为第 4 层换能器安装位置；浅蓝色线为各层换能器之间超声波传输的路径；红线表示换能器与最高水位的垂直距离。1.1，1.2 左右岸 2 个探头组成 1 层换能器，可以测出相对河底往上 1.20 m 处的层流速，以此类推至其他 3 对换能器。

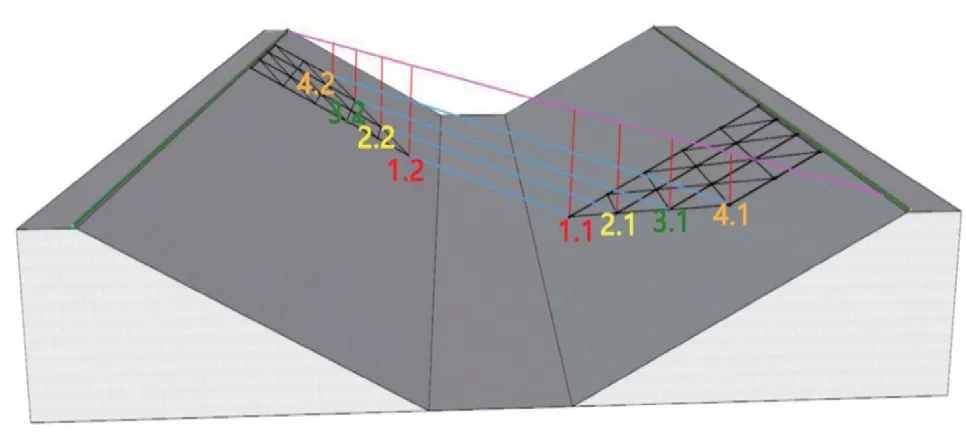
图 4 4 层换能器安装示意图

2.2 换能器固定方式

陶岔主干渠时差法超声波流量计的换能器采用预制托盘固定，托盘由横担、滑轨、斜拉撑、换能器滑轨小车、滑轨小车底托、滑轨小车推拉管、连接板和固定板组成，通过预制托盘固定安装，施工方便，框架结构稳定，换能器在水下环境中固定牢固，保证换能器在接收超声波信号时稳定。

3 时差法超声波流量计的比测分析

3.1 比测内容

陶岔干渠时差法超声波流量计比测实验中，常规测验方法采用转子式流速仪法、走航式 ADCP法，测得的流量数据同相应时段时差法超声波流量计数据进行对比分析，以常规测验方法的数据为基准，着重分析时差法超声波流量计监测的流量数据成果精度及误差来源与控制。

3.2 比测方案

3.2.1 转子式流速仪法流量测验

转子式流速仪法测验方案采用 LS 25-3A 型旋桨式流速仪在时段流量稳定的条件下测量全断面流量，测验方式如下：测速垂线为 11～12 条，垂线测点为 3 个，测点测速历时为 60 s，测深和测速的起点距分别为 8.0，10.0，15.0，20.0，30.0，35.0，41.0，43.0，50.0，55.0，61.0，63.0 m。

3.2.2 走航式 ADCP 流量测验

走航式 ADCP 采用 1 200 kHz 的瑞普 ADCP 进行流量测验。水情平稳时，每次测验至少施测 2 个测回，测回间流量相对误差不超过 5%，平均历时一般在 20 min 以内；水情涨落变化快时，施测 1 个测回。通过 WinRiver Ⅱ 软件计算 GGA（GPS 跟踪模式）或 BTM（底跟踪模式）下的实测流量、断面面积和平均流速。

3.2.3 时差法超声波流量计测验

陶岔干渠安装的 Quantum 时差法超声波流量实时监测系统测量采样间隔为 300 s，每 5 min 时差法超声波流量计完成 1 个流量数据的采集。系统内置时差法超声波信号处理及流量计算软件。流量成果使用自带软件计算，其中校准系数k2值为前期实验所得，计算所需水位为现场气泡压力式自记水位计提供。

3.3 比测分析

陶岔 Quantum 时差法超声波流量实时监测系统自 2019 年 6 月 25 日开始运行至 9 月 26 日，分别采用走航式 ADCP 和转子式流速仪法与该系统的时差法超声波流量计进行同步流量比测，共计 31 个测次。

比测期间，干渠内水位变化范围为 148.69～149.61 m，流量变化范围为 205～354 m3/s，比测测点主要集中在水流相对稳定时段。常规流量测验和时差法超声波流量计 2 种方法测得流量对比如图 5所示。从图 5 可以看出： 由于受水流脉动强弱影响，大流量级时，常规流量测验方法和时差法超声波流量计测得的流量误差较大；在小流量级时，两者误差较小；其中部分流量级存在一定系统误差，具体原因尚待分析。

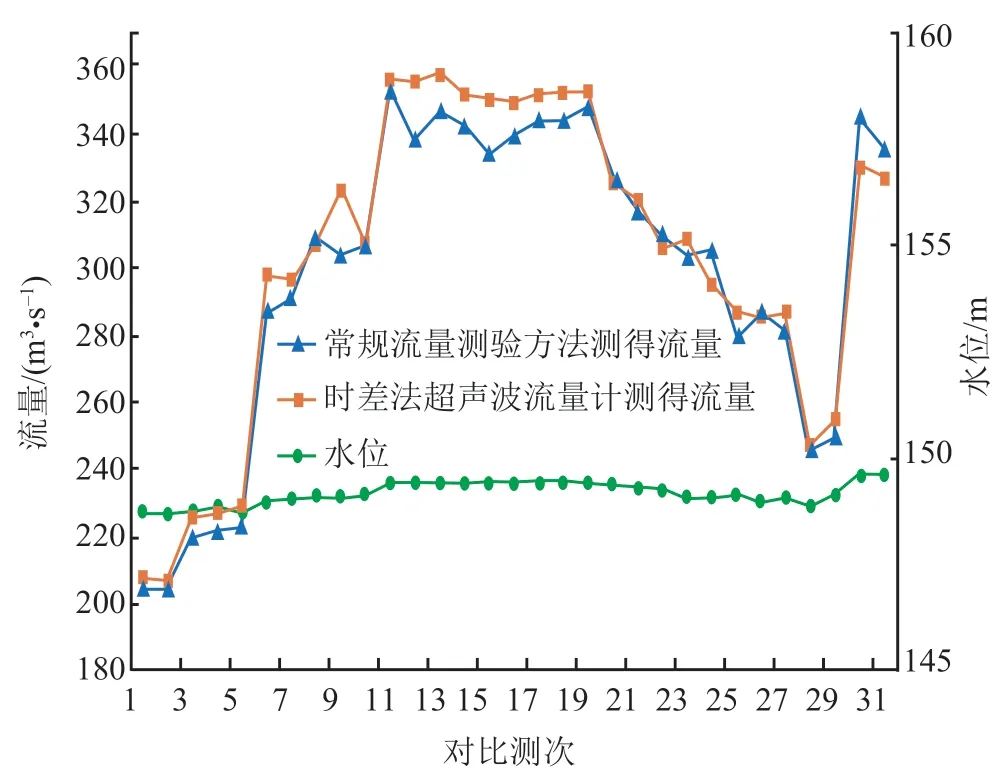
图 5 常规流量测验方法和时差法超声波流量计2 种方法测得流量对比

3.3.1 成果精度评定

以常规流量测验方法测得流量为基准，计算样本数据时差法超声波流量计测得流量的平均相对误差δ，计算公式如下：

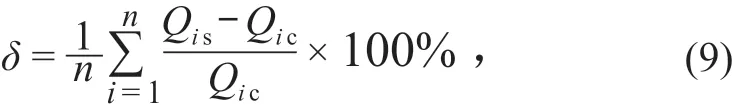
计算相对误差标准差S，公式如下：

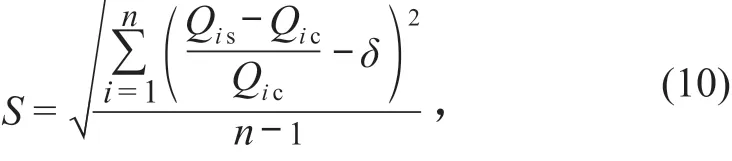
式中：Qis为第i个测次时差法超声波流量计测得流量；Qic为第i个测次常规流量测验方法测得流量；n为样本数量；S为时差法超声波流量计测得流量的相对误差标准差。

经过计算，平均相对误差δ=1.28%，相对误差标准差S= 2.30%，取 2 倍相对误差标准差估算其置信水平为 95% 的总不确定度为 4.60%[6]。

借鉴流速仪法单次流量测验允许误差，精度满足 GB 50179—2015《河流流量测验规范》中，一类精度站中水位级基本资料收集或水资源管理所要求的精度，即随机不确定度不应超过 6%，系统误差不超过 ±2% 的要求[7]。

3.3.2 误差来源分析

流量测验误差可分为随机、未定系统、已定系统的误差，以及伪误差。随机误差应按正态分布，采用置信水平为 95% 的随机不确定度描述；未定系统误差采用置信水平不低于 95% 的系统不确定度描述；已定系统误差，应进行修正；含有伪误差的测量成果应剔除，本次比测实验成果数据采用前已对伪误差的数据进行了剔除。经分析，时差法超声波流量计测得流量误差在本次比测实验中的来源主要有以下几个方面：

1）前期k2值的率定是以常规流量测验方法获取数据为基准的，流量测验本身存在随机误差[8]，采用k2值后误差带入时差法超声波流量计系统。

2）比测实验中，以常规流量测验方法作为基准，但其测验成果同样存在误差，且误差范围无法精准评估。

3）时差法超声波流量计在测量水层平均流速方面存在系统误差，其误差会带入流量计算中。

4）比测时 2 种测验方式外部条件无法完全一致，如水流条件、时间同步等方面，会造成误差。

4 时差法超声波流量实时监测系统运行效果

陶岔干渠自安装 Quantum 时差法超声波流量实时监测系统以来，经过对时差法超声波流量计调试、率定、比测等过程，于 2020 年 1 月 1 日正式运行。

实时监测系统采集的水层流速数据和经过模型计算得到的断面流量数据会存储在系统计算机内。通过 RTU 接入网络可将数据经多通道转发至各数据中心，实现数据多备份。原始数据主要为多层流速数据，可对流速数据进行分析，必要时建立流量计算模型进行二次流量计算，实现数据的可开发性。结合自行开发的中心站处理软件，可实现流量实时监测和历史数据查看与导出。经过比较：采用常规流量测验方式监测干渠流量，1 a 需要上百个流量测次，同时还要进行水位-流量关系分析与定线，耗费大量人力和物力资源；采用时差法超声波流量实时监测系统实现流量远程连续监测，5 min 即可完成1 次流量测试、计算、上报过程，大大提高了水文监测效率。

5 结语

在南水北调中线陶岔干渠应用以时差法超声波流量计为重要组成的流量实时监测系统进行流量监测，采取现场存储、转发，中心站接收的模式，实现数据双备份，确保了资料安全，满足了水文自动化建设要求，推进了水利信息化建设，提升了水文监测能力，在南水北调中线工程的水量监测，丹江口水库的精准调度、水资源管理中发挥了重要作用。其分层流速数据可根据需求进行最小采集间隔设置，满足水文分析计算、水资源管理等需求，有应用分析价值。

在应用管理上，Quantum 时差法超声波流量实时监测系统投产后，还须加强流量比测资料的收集和相关参数的适用性验证，在使用过程中不断细化参数。同时借助 Quantum 时差法超声波流量实时监测系统也可开展规整大型渠道分层流速分布研究，分析优化不同水位变幅、水深、水面宽等条件下流速沿水深垂线分布规律，优化理论速度系数k1，提高流量测验精度。