舰船磁场垂向分量推算其三分量的傅里叶方法∗

王 鲸 禤予文 杨明明

（1.中国人民解放军92601部队 湛江 524009）（2.中国人民解放军91388部队 湛江 524022）

1 引言

舰船磁场是舰船的重要物理特征，是舰船隐身性能的重要指标之一。现代水中兵器和航空磁探测一般使用舰船磁场在舰船坐标系下的投影来作为触发、控制引爆和探测的信号源［1］。舰船磁场在相应坐标系下的投影分别称为磁场成为磁场纵向分量、横向分量和垂向分量，统称为磁场三分量，在舰船磁性处理中需要对磁场三分量进行测量以提高舰船磁隐身性能。

采用三分量磁传感器进行舰船磁场三分量的测量是最为直接的方法，但三分量磁传感器造价成本高、技术复杂、安装要求高，实际使用中存在测量前需检测调整其三轴正交性等不便。而单分量磁传感器的成本和安装要求低，且不需要调整正交性，使用方便，但其只能获取舰船磁场的某一分量，需要由该分量推算其他分量。针对上述问题，文献［2～3］分别从舰船磁场的Laplace方程出发，建立了磁场垂向分量与其他两个分量的积分表达式，实现了由磁场垂向分量推算磁场纵向和横向分量。

上述方法存在测量面的剖分，复杂的积分奇异处理和大量的积分计算等不足。为此，本文引入空间二维傅里叶变换，建立相应的推算模型，可避开积分奇异处理和积分计算。在此基础上，探讨测量面长度和宽度对推算方法的影响，确定适用性条件。

2 基于傅里叶变换的推算方法

2.1 磁场三分量的频率域关系

如图1所示，舰船下方某无限大平面S将场域空间分成两部分V1和V，所有的磁源（包括铁磁物质和传导电流）都被限制在V1内。

图1 磁源与场域位置示意图

V可以看成是由两个闭合面限定的区域（S和伸展到无限远的S∞），该区域内没有电流分布（J=0），则标量磁位φ(x，y，z)满足拉普拉斯方程：

由式（12）可以看出磁场三分量的空间傅里叶变换存在点对点的简单线性关系，即经空间二维傅里叶变换后的磁场某分量在每一波数（u或v或）处的能量值仅与其他分量在该波数相对应波数的能量值有关。上述推导过程是建立在测量点位于xoy平面内的，即空间二维傅里叶变换是针对x和y坐标进行的，波数u和v的取值与x和y坐标有关，因此由磁场的Bx或By分量无法直接由式（12）计算Bz分量。若测量发生在yoz平面内则可由Bx计算By或Bz，若测量发生在xoz平面内则可由By计算Bx或Bz，此时式（12）相应的变换为

由 Bx计算 By或 Bz：

由 By计算 Bx或 Bz：

2.2 基于空间傅里叶变换推算的离散模型

从上面的分析不难看出，在频率域内实现磁场单分量之间推算的重点是二维傅里叶变换及其反变换。为了便于计算机上实现，需要将式（2）离散化。

假设磁场测量位于如图2所示，全部磁场测量位置形成采样间隔均匀的（2M+1）X（2N+1）点阵，依据文献［4］，可将式（2）离散化为：

图2 测量位置示意图

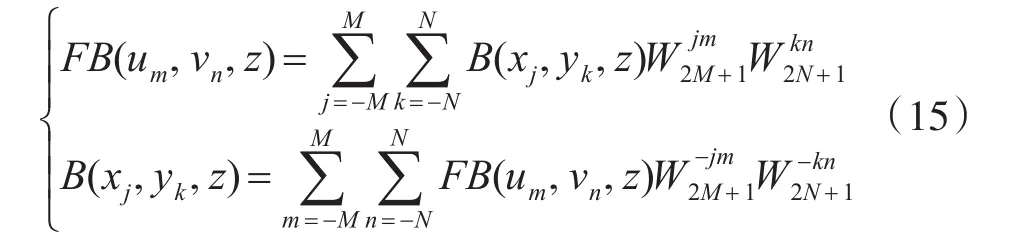
其中B和FB分别为某磁场分量及其傅里叶变换 ，W2M+1为 常 数e-i2π/(2M+1)，W2N+1为 常 数e-i2π/(2N+1)，um和 vn的取值满足 Nyquist采样定理要求，具体为

在测量得到磁场垂向分量后由式（13）和式（14）进行傅里叶变换后，逐频率点（波数）由式（12）计算磁场x，y分量的傅里叶变换，再进行傅里叶反变换即可求得该分量磁场值。

3 数值算例分析

采用单个长旋转椭球体来模拟舰船总体磁场特性，以数个磁偶极子来模拟舰船局部磁场是舰船磁场建模常用的方法，称为混合阵列模型［5］，本文采用参数如表1中的椭球体和磁偶极子开展数值算例分析。测量面中心坐标为（0，0，20）测量面在x方向的长度Lx和y方向的长度Ly分别为200m和150m，测量点在x方向和y方向的间距分别为5m和7.5m。

表1 磁模拟体参数表

数值分析的具体过程：1）由磁模拟体参数计算各测量点的磁场值作为理论值，在磁场垂向分量的理论值上叠加幅值为±10nT的随机噪声作为其测量值；2）由磁场垂向分量的测量值采用上述基于空间二维傅里叶变换的数值模型计算磁场纵向分量和横向分量，记为磁场推算值；3）比较分析磁场推算值与理论值的差异。比较结果见图3～图6，可以看出：在测量面的中心较大区域内，推算值与理论值吻合较好。为消除随机测量噪声的干扰，经多次计算后发现：Bx和By的相对均方差［6］分别不超过2.5%和1.5%。图7和图8分别为y=0米测线的Bx和x=0m测线的By的最大相对误差［6］，从图中可以看出，在测量面的边缘区域误差较大，在测量面的中心区域最大误差不超过5%。

图3 Bx理论值与推算值比较图

图4 Bx理论值与推算值（y=0m）比较图

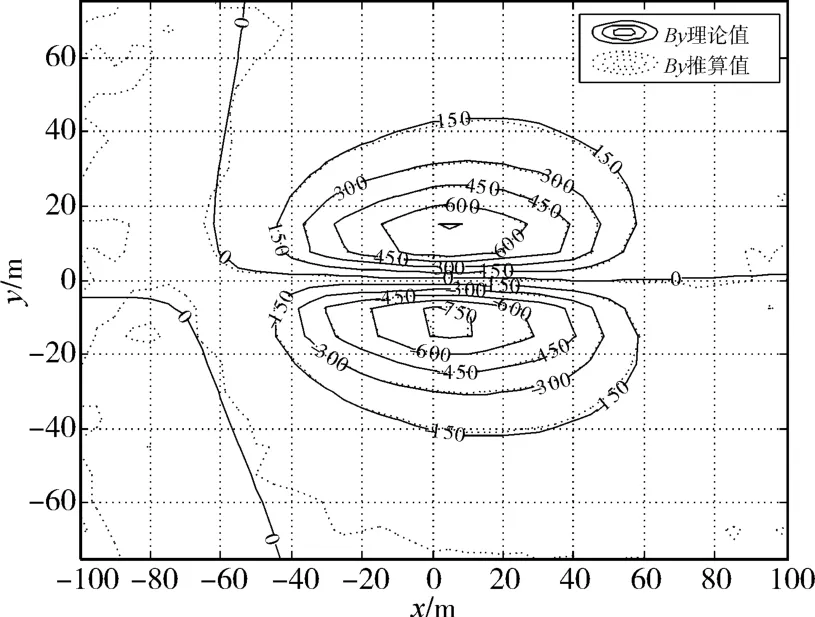
图5 By理论值与推算值比较图

图6 By理论值与推算值（x=0m）比较图

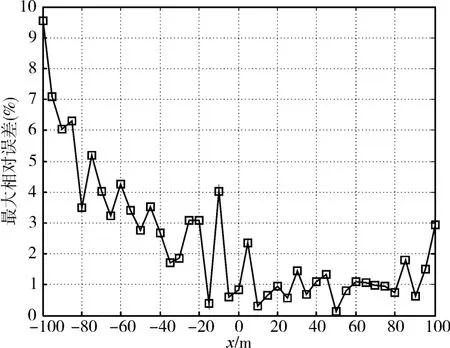
图7 Bx最大相对误差（y=0m）图

图8 By最大相对误差（x=0m）图

采用本文方法进行磁场分量推算时，主要存在两类方法误差：一是窗效应误差，由于采用有限区域内的求和带代替无限区域的积分，出现类似于时频信号频谱分析时，对信号有限截取相当于加了矩形窗，从而产生频谱泄露误差；二是边缘效应误差，磁场测量值的离散傅里叶变换需要在波数域采样（um和vn取离散值），求测量值傅里叶变换的过程中磁场值经过周期性复制延拓，参与变换的信号是由居于中心的实测值和无限多个分布在其周围的“虚像”构成，而傅里叶反变换随距离衰减，距离“虚像”越远的地方越小，因此测量面边缘距离“虚像”越近，误差较大。降低两类方法误差的途径主要为尽可能增大测量面，一般需要在感兴趣的区域外各增加30%的区域作为测量面。图9为Ly=150m，相对均方差随Lx的变化图，图9为Lx=200m，相对均方差随Ly的变化图，从图中可以看出，相对均方差随Lx或Ly的增大而减小，这是因为随测量面的增大，参与傅里叶变换的磁场信息多，频谱泄露误差小。

图9 相对均方差随Lx的变化图

图10 相对均方差随Ly的变化图

4 结语

本文基于空间二维傅里叶变换建立了由磁场某分量推算其矢量的方法，该方法无需测量面单元剖分、复杂的积分计算以及积分奇异处理。利用磁椭球体和磁偶极子混合阵列模型的数值分析算例验证了方法的可行性，结果表明推算精度较高。初步探讨测量面长度和宽度对推算方法的影响，分析表明该方法要求测量面足够大。考虑到实际的舰船磁场测量方式，本文方法更适合于动态磁性检测方式下的磁场分析场合。下一步，针对固定式消磁设施中磁场面较窄、磁场信息获取有限等实际，引入扩边和内插等处理手段，改善和提高本文方法的适用性，并开展实验验证研究。