基于M估计的遭遇段弹目运动数据拟合方法∗

裴 喆

（92941部队 葫芦岛 125000）

1 引言

通常利用光学测量防空导弹遭遇段导弹和目标的x、y、z方向运动数据，对这6组数据进行拟合除差处理是计算导弹战斗部毁伤、脱靶量等参数的重要依据［1～3］。如果其中1组甚至多组数据的拟合精度不高，那么势必影响导弹性能分析。目前经常采用普通最小二乘（Ordinary Least Squares）拟合（以下简称OLS拟合）方法，数据不含粗差时拟合精度较高［1，3］。但是由于设备测量误差、弹目尾焰红外成像面积散布误差、事后人工选点误差等因素影响，实测数据有时包含少量粗差，尤其小幅值粗差。OLS拟合抗粗差能力弱，致使拟合精度下降。为此本文研究基于M估计的遭遇段弹目运动数据拟合方法，并对其抗粗差能力和拟合效果进行仿真验证。

2 M估计与Tukey权重函数

OLS拟合给予每个测量数据的权重均为1，且拟合目标是使残差平方和最小，因此拟合结果受粗差影响较大［4］。稳健拟合的目的就是减小粗差影响，目前主要有L估计、R估计、M估计等方法。其中M估计是经典极大似然估计的推广，被称为广义极大似然估计［4～5］。基于M估计的稳健拟合方法采用特定的权重函数构建一个增速较低的残差函数，拟合目标是使该残差函数之和最小，所以残差越大，权重越小，达到抵抗粗差的目的［6～7］。

M估计常用的权重函数有Huber、Tukey、Ham⁃pel等。本文采用Tukey权重函数，其表达式如式（1）所示［8～9］：

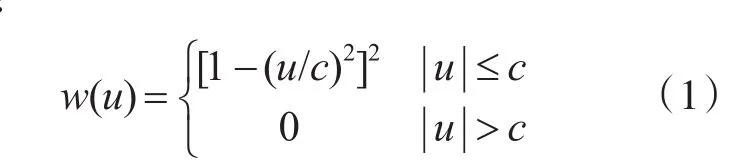
式中，w为权重大小（0≤w≤1）；c为调节系数；u为标准化残差，计算公式如下［9］：

式中εn为拟合残差；S为稳健估计量的尺度，通常用残差εn的中位数绝对离差MAD计算，当εn服从正态分布时，利用式（3）计算的S是该正态分布标准差的无偏估计［9～10］。

中位数绝对离差MAD的计算公式为［9～10］：

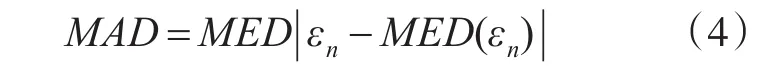
式中MED为残差εn的中位数。MED和MAD分别是稳健拟合中重要的位置测度和尺度测度［11］。

调节系数c取常用值4.685时，Tukey权重函数如图1所示。

证据留痕 积极应对（李远强等） ....................................................................................................................7-57

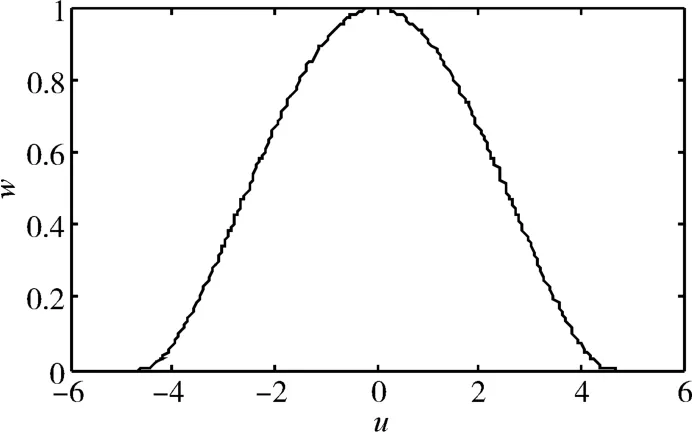
图1 Tukey权重函数（c=4.685）

由式（1）和图1可知，对于|u|＞c（即|εn|＞cS）的两端残差，Tukey函数赋予的权重w均为0，因此它是 有 淘 汰 域 的 权重 函数［5］；对 |u|≤c（即|εn|≤cS）的中间段残差也进行权重分配，越靠近中心其权重w越接近1。同时可知c值越小，其抗粗差能力越强，这也是本文用来识别小幅值粗差的理论依据。

3 不含粗差时的拟合结果分析

假设防空导弹和目标在遭遇段150ms时间内均作匀速直线运动是成立的［3］，以导弹y方向运动为例，其真值数据yM0（ti）可由式（5）表示。

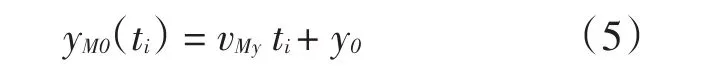
式中，ti为采样时间（i=1，2，…，n），yM0（ti）为位置真值，vMy为速度真值，y0为位置截距真值。

测量误差用ε（ti）表示，则yM0（ti）的测量数据yM（ti）表示为

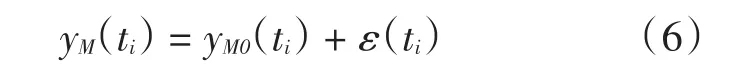
下面对yM（ti）不含粗差时OLS拟合和M估计拟合结果进行对比分析。设置ti=［10.01s，10.15s］，采样周期为10ms，则采样个数为15。设vMy为-50m/s，y0为100m，由式（5）得到yM0（ti）。再设ε（ti）为白噪声误差，即ε（ti）～N（0，σ02），σ0取 0.15m，ε（ti）不含粗差（幅值绝对值均小于 3σ0），由式（6）得到 yM（ti）。拟合结果（vMy的估计值 vMye和 y0的估计值 y0e）如表1所示，拟合残差特征量（标准差σMy、MAD以及尺度S）如表2所示。

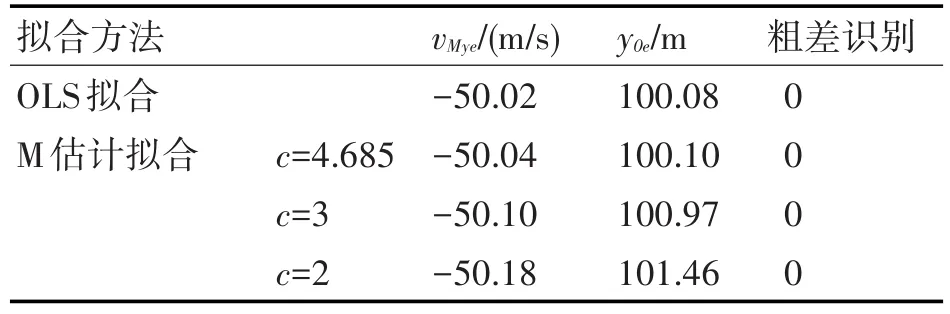
表1 yM（ti）不含粗差时的拟合结果

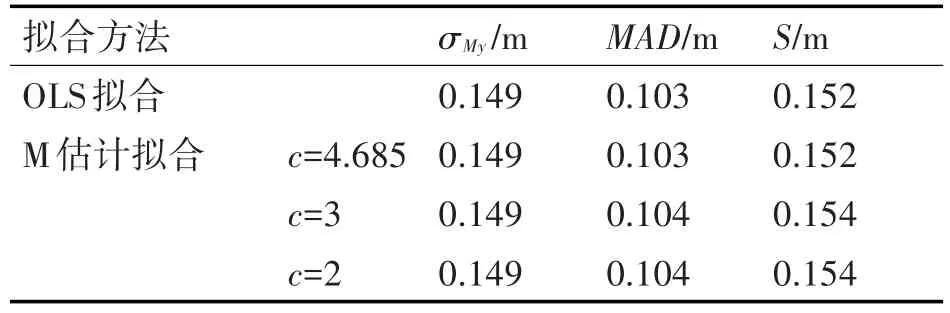
表2 yM（ti）不含粗差时的拟合残差特征量

分析表1和表2可知：

1）从拟合结果看，不含粗差时两种拟合得到vMy和y0的估计精度都很高，其中OLS拟合与c=4.685时M估计拟合的精度相当。当c值从4.685逐渐减小到2，vMy和y0的估计精度逐步下降，但下降幅度非常小，可知拟合仍是稳健的，并未将正常数据误判为粗差。这是因为由正态分布可知，1次测量误差绝对值超过2σ0的概率仅为4.56%［12］，即在22次测量中只有1次的误差绝对值超过2σ0，而yM（ti）的采样个数仅为15。

4 包含粗差时的拟合仿真验证

4.1 基于M估计的拟合方法及步骤

本文主要讨论幅值绝对值在（3σ0～3.5σ0）范围内的粗差，因为这种小幅值粗差较为“隐蔽”，OLS拟合很难识别它们。由于双站光学同帧画幅数据已经有效减小各种测量误差［2～3］，粗差比例很少大于15%，因此对于上节中采样个数为15的yM（ti）数据，只讨论包含1～2个粗差的情况。

基于M估计的拟合方法及步骤如下。

1）取最小c值识别粗差

调节系数 c最小取 2，对 yM（t）i进行 M 估计拟合，根据残差|εn|＞2.5S的准则识别粗差，标记粗差的位置和个数。如果未识别出粗差则对yM（ti）进行OLS拟合。

2）增大c值替换粗差

逐步增大c的取值（每次增大0.1），对yM（ti）进行M估计拟合并且识别粗差，如果识别的粗差与c=2时所识别粗差的位置和个数均相同，就将粗差替换为当前c值对应的拟合数据，因为c值越大拟合精度越高；直到识别粗差的位置或个数与c=2时所识别粗差的不同，即可停止增大c值。最后再对粗差替换后的数据进行OLS拟合。

4.2 只包含1个粗差时的仿真验证

与位于其他位置相比，1个粗差位于数据一端时OLS拟合识别它更困难。为此在上节中无粗差的yM（ti）末端加入1个粗差（幅值为3.2σ0），拟合结果如表3所示，拟合残差特征量如表4所示。

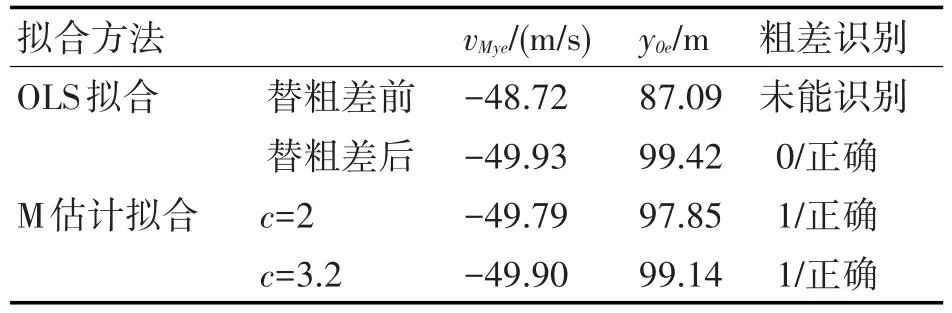
表3 1个粗差位于yM（ti）一端时的拟合结果

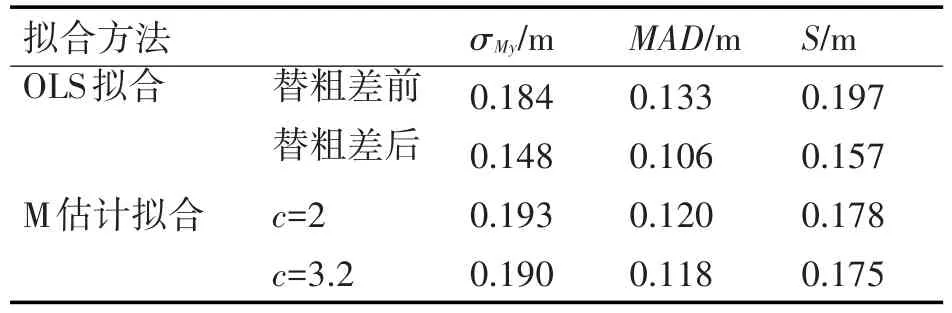
表41 个粗差位于yM（ti）一端时的拟合残差特征量

分析表3和表4，并与表1、表2对比，可知：

1）受粗差影响，OLS拟合估计值vMye、y0e均没有不含粗差时的估计值准确。依据通常采用的残差绝对值大于3σMy的准则，OLS拟合未能识别出粗差。

2）c值从2～3.2，M估计拟合均能正确识别粗差，c=3.2时的拟合估计值比c=2时的准确。将粗差数据用c=3.2时的拟合数据替换后，再次OLS拟合的估计值已逼近真值，相比粗差替换前的估计精度明显提高。

3）与不含粗差相比，包含粗差时的拟合残差标准差σMy均有所增大，但M估计拟合的MAD和S增幅较小，可见二者的稳健性较好。同时正因为MAD和S的增幅较小，本文识别粗差准则采用|εn|＞2.5S，而不是常用的|εn|＞3S。

4.3 包含两个粗差时的仿真验证

4.3.1 含两个同向粗差时的拟合效果

与位于其他位置相比，两个同向粗差集中靠近数据一端时，OLS拟合识别更为困难。为此，在无粗差的yM（ti）末端加入两个同向粗差，幅值均为3.3σ0，拟合结果如表5所示，拟合曲线如图2所示。图中，yM（ti）、yM2（ti）分别为替换粗差前、后的测量数据曲线，yMO（ti）、yMO2（ti）分别为替换粗差前、后的OLS拟合数据曲线，纵坐标统一用yM表示。

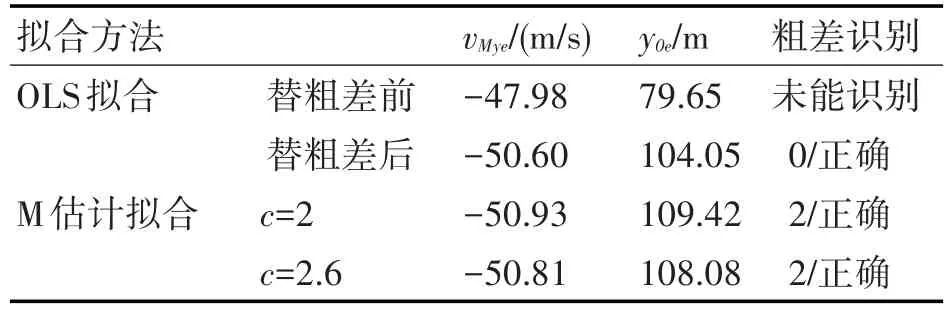
表5 两个同向粗差集中于yM（ti）一端时的拟合结果

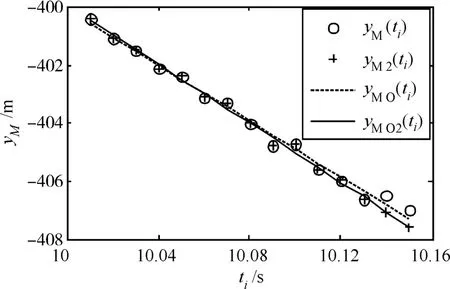
图2 2个同向粗差集中于yM（ti）一端时的拟合曲线

由表5和图2可知，两个粗差对OLS拟合曲线有明显的拉偏影响，粗差替换后拟合效果明显改善。c值从2到2.6时M估计拟合均能正确识别出两个粗差，且未将正常数据误判为粗差。

4.3.2 含两个反向粗差时的拟合效果

对于两个反向粗差，正、负粗差分别位于数据两端形成“跷跷板”式情形相比位于其他位置的情形对拟合影响更大。OLS拟合识别它们更为困难为此，在无粗差的yM（ti）两端加入两个反向粗差，幅值分别为-3.3σ0和3.3σ0，拟合结果如表6所示，拟合曲线如图3所示。

由表6和图3可知，反向粗差分布于两端比同向粗差集中于一端对拟合的影响还要严重，因此仅在c从2～2.3时M估计拟合能正确识别出两个粗差。粗差替换后拟合估计值vMye、y0e的准确性明显提高。

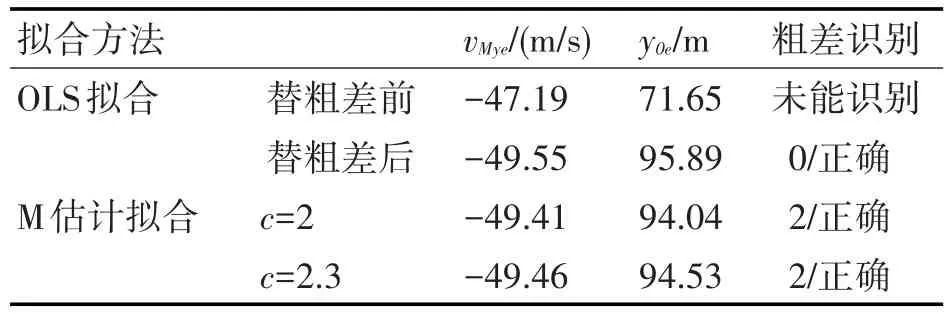
表6 两个反向粗差分布于yM（ti）两端时的拟合结果

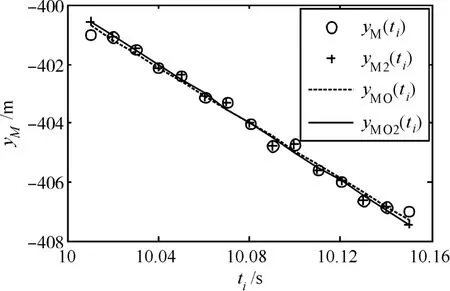
图3 两个反向粗差分布于yM（ti）两端时的拟合曲线

5 结语

本文研究了基于M估计的遭遇段弹目运动数据拟合方法。对于测量数据中的少量小幅值粗差，方法通过选取较小的Tukey权重函数调节系数c值，可在正确识别粗差的同时得到较为稳健的拟合结果；而在此基础上增大c值又可提高粗差替换值的准确性。研究表明：当数据中小幅值粗差比例不大于15%时，本文方法可有效识别这些粗差，粗差替换后的拟合效果明显优于普通最小二乘法。