一种TDCS自适应粒子群导频优化设计算法

李 明，任清华，李夏昭，吴佳隆

(空军工程大学 信息与导航学院，西安 710077)

0 引 言

为了应对快速增长的无线宽带通信需求，需要更智能的通信信号波形来解决频谱资源短缺和复杂通信干扰问题。变换域通信系统(transform domain communication system, TDCS)作为认知无线电的候选传输技术，其利用动态频谱接入技术构建基函数实现数据调制，提升频谱使用效率的同时具有主动、智能的抗干扰能力[1-5]。

无线通信信道往往是复杂、时变的，需要准确的信道估计来均衡信号在传输过程中产生的畸变。为了估计信道响应，需要在发送数据中插入已知的导频点[6]，导频插入的位置和功率是影响估计性能的主要因素，本文将主要研究适用于变换域通信系统的频域导频插入优化算法。文献[7]指出在子载波连续的通信系统中，以信道估计均方误差(mean square error, MSE)最小为准则，等间隔等功率的导频设计是最优的，而TDCS的频谱是非连续的，不可用频点处存在电磁干扰无法进行准确的信道估计，需要一种适合TDCS的非等间隔导频优化设计方案。文献[8]针对TDCS无线信道具有稀疏特性，采用压缩感知技术获得了较好的估计性能，然而其未考虑子载波不连续的情况，并且需要每个频点都参与信道估计并构造测量矩阵，开销较大。文献[9]对等间隔等功率的插入方法进行了修正，将基函数频谱进行分组，在每组第1个可用频点的位置插入导频，但其设置简单并不是最优解。文献[10]提出了一种非连续子载波系统的次优导频设计，将导频位置拟合为3次函数曲线，根据不可用频点位置计算参数，产生最优导频位置，然而面对频谱随机分布的TDCS基函数，曲线拟合方法并不适用。文献[11]对不连续频带进行分组合并，推导频带中的导频数量，然后用遍历法搜索找出次优的导频位置，此方法虽降低了穷搜索产生的巨大运算量，但其计算效率仍不高且优化能力有限。综上所述，需要一种适合TDCS的导频优化算法，在降低计算量的同时能准确解出最优导频序列。为此，提出了一种自适应粒子群导频优化算法，首先分析TDCS特点构建信道估计模型和导频优化模型，其次设计适应值函数与自适应惯性权重，通过粒子群算法求解最优导频序列，解决TDCS在复杂干扰环境下的信道估计问题。

1 TDCS信道估计模型设计

基于传统的TDCS通信模型，加入信道估计模块，设计了采用循环前缀 (cyclic prefix，CP)的TDCS信道估计模型，如图1。

图1 TDCS 信道估计模型Fig.1 TDCS channel estimation model

首先，TDCS发射端通过对周围电磁环境进行感知，将整个频带分为N个频点，通过对频谱向量A={A0,A1,…,AN-1}进行0，1动态调整，实现基函数与干扰正交，如图2，其中，不可用频点位置处频谱模值设为0，{Ak=1,k∈Ωc}。

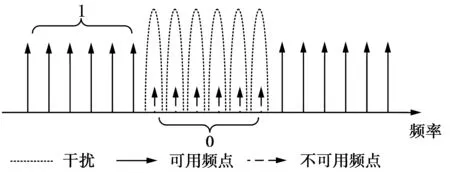
图2 基函数频谱向量图Fig.2 Spectrum vector of basic function

频谱向量A与伪随机相位E={ejθ0,ejθ1,…,ejθN-1}相乘，经过傅里叶逆变换后得到TDCS基函数，与比特数据一起进行循环码移位键控 (cyclic code shift keying，CCSK)调制，产生TDCS传输信号[12]。插入导频完成后，添加CP以防止符号间干扰。然后信号通过发射天线进入无线多径信道。TDCS宽带多径衰落信道的离散时间模型为

(1)

(1)式中：L代表信道抽头的数量；hl代表第l个抽头的信道增益。移除CP后，接收到的信号可以表示为

y=x⊗h+w

(2)

(2)式中：x=[x0,x1,…,xN]T代表发送信号；y=[y0,y1,…,yN]T代表接收信号；w=[w0,w1,…,wN]T代表加性高斯白噪声；⊗代表卷积运算。 (2)式变换为矩阵形式为

y=Gx+w

(3)

(3)式中，G是由信道冲击响应组成的循环矩阵，表达式为

(4)

接收信号经快速傅里叶变换(fast Fourier fransform，FFT)变换到频域，进入均衡滤波器进行频域均衡，消除多径衰落的影响。采用最小均方误差均衡方法，均衡后的频率信号可以表示为

(5)

(5)式中，DH=diag(H)，H=[H0,H1,…,HN]T是信道频率响应。时域接收信号与接收端产生的基函数进行相关解调得到接收数据d(t)。

2 信道估计分析

由于频域导频更适合快时变信道，被广泛应用于通信系统的信道估计中，下面对TDCS频域导频插入方式的信道估计性能进行推导分析。对(2)式进行FFT变换得

Y=DXH+W=DXFLh+W

(6)

(6)式中：X=[X0,X1,…,XN-1]T，Y=[Y0,Y1,…,YN-1]T分别为频域发送信号和接收信号；DX代表X构成的对角矩阵；FL为归一化矩阵的前L列。接收端导频数据可表示为

YP=DPFLh+Wp

(7)

(7)式中：P=[P1,P2,…,PNP]T为频域导频序列；WP为归一化矩阵导频位置所对应行组成的Np×L维矩阵。对h进行最小二乘法估计得

(8)

为了能准确估计出h，DPFP应为列满秩矩阵。导频数量应满足NP≥L。通过估计出的信道函数可以得到数据频点处的信道频域响应

(9)

FD的定义与FP相同，导频辅助的信道估计以信道频域响应的MSE最小作为设计准则，根据 (9) 式，可以推导出数据频点处的估计误差MSE为

(10)

(10)式中，‖A‖代表矩阵A的F-范数。当Np>L时，矩阵FP不再是方阵， (10) 式可以改写为

(11)

根据 (11) 式可以看出，数据频点处的MSE性能受导频位置和功率的影响。当TDCS基函数子载波连续时，等功率等间隔的导频分布是最优的， (11) 式可写为

(12)

(12)式中：|FDFP+|2代表矩阵FDFP+中每个元素模值的平方；ND为数据频点个数；|Pi|-2为单个导频的功率。 (12) 式为MSE理论最小值，可以看出导频数量、功率，传输信道的噪声及信道时延个数都会对MSE的性能产生影响。

3 自适应粒子群导频优化设计

3.1 优化模型构建

DSMSE=

(13)

(13)式中，ED为数据位置的平均功率。可以看出，不可用频点处的信号畸变不影响DSMSE的变化，这使得DSMSE更准确地表达了导频的优化方向，最大程度降低了信号畸变产生的误码率损失。导频位置和功率的优化模型可建立为

KP∈Ωc

(14)

3.2 自适应粒子群算法

本文采用粒子群优化算法(particle swarm optimization，PSO)求解导频优化问题。PSO算法是一种群体智能优化算法，广泛应用于复杂优化问题的求解中。

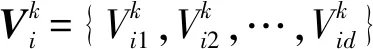
(15)

(15)式中：ω为惯性权重；c1,c2为非负常数，为学习因子；r1,r2为0到1之间的随机数。传统的粒子群算法存在收敛较慢，容易陷入局部最优的缺点[14-15]，一般通过调整惯性权重ω来平衡算法的全局搜索能力和局部寻优能力，典型的有线性递减权重粒子群算法，其权重随迭代次数增加而线性减少，迭代初期较大的ω值可以保持算法的全局搜索能力，迭代后期较小的ω值有利于局部的精确搜索。为降低TDCS导频设计复杂度和提升ω的特性，设计了一种自适应惯性权重粒子群优化算法(adaptive inertia weight particle swarm optimization, AIWPSO)，其基本理念为让粒子具有识别局部最优解和跳出局部最优的能力，同时能感知粒子群的进化速度，调整粒子群的全局搜索能力，自适应惯性权重ω的设计为

(16)

(16)式中：ωstart为初始惯性权重；f为当前粒子的适应值；favg为当前粒子群的平均适应值；fprevbest为上次迭代粒子群全局最优值；fcurbest为当前粒子群最优值；μ和λ为取值[0,1]的适应值调整因子。当fprevbest与fcurbest差异较大时，粒子群进化速度较快，较大的ω值可以提升粒子的搜索范围，当二者差值较小时，ω值变小有利于粒子进行精确搜索；当favg与fcurbest差异较小时，当前粒子群聚集度较高，此时粒子获得较大的ω值从而避免陷入局部最优。自适应粒子群算法导频优化流程具体操作步骤如下。

1)初始化粒子群的位置和速度，可根据导频的数量设置单个粒子的维度，粒子可代表导频位置或功率，根据 (13) 式计算此时导频序列的适应值，更新个体极值和群体极值；

2) 判断粒子是否满足收敛条件(达到收敛精度或者最大迭代次数)，不满足进行下一步，否则转至步骤6；

3) 计算当前群体适应值均值，按照 (16) 式更新权重ω；

4) 更新群体中每个粒子的速度和位置，计算每个粒子的适应值，并更新个体极值和全局极值；

5) 迭代次数加1，执行步骤2)；

6) 返回此时的全局极值即为最优解。

3.3 算法复杂度分析

4 仿真结果与对比分析

4.1 导频优化设计性能验证

为了验证自适应粒子群算法在单不可用频带和多不可用频带下的导频优化设计能力，设计了2种干扰环境，干扰采用2种部分频带干扰，模拟2种TDCS传输基函数。TDCS基函数总子载波数N=128，其中,单干扰频带的基函数可用频点为{1,…,44,76,…,128}，多干扰频带的基函数可用频点为{1,…,24,46,…,82,109,…,128}。添加CP长度为32，导频数Np=16，导频的平均功率为1。多径信道的抽头数L=16，最大多普勒频移为20 Hz，符号采样周期为10-4s。自适应粒子群算法的参数设置为：粒子数30，迭代次数5 000，ωstart=0.9。首先，采用自适应粒子群算法按照等功率分配求得最优导频位置，之后再对每个导频的功率进行优化分配。在单干扰环境下导频优化的位置结果为

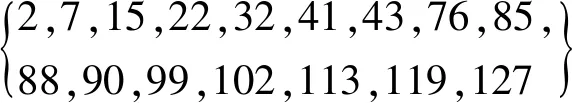
其对应的导频功率为

在多频带干扰环境下的导频位置优化结果为

相应的导频功率为

图3、图4分别为在单干扰频带和多干扰频带环境下优化算法的适应值函数进化曲线。其中线性递减权重的起始和终止权重分别为0.9和0.4；最优导频指采用穷搜索算法得到的最优导频序列。从图3可以看出，自适应权重较传统线性递减权重在搜索前期进化速度更快，并且收敛结果更加接近最优值。由图4可知，在多干扰频带下本文设计算法仍能保持快的进化速度和较强的优化能力，而线性递减权重在多频带环境下的进化速度较慢，收敛效果并不理想。

图3 单干扰频带进化曲线Fig.3 Evolution curve of single interference band

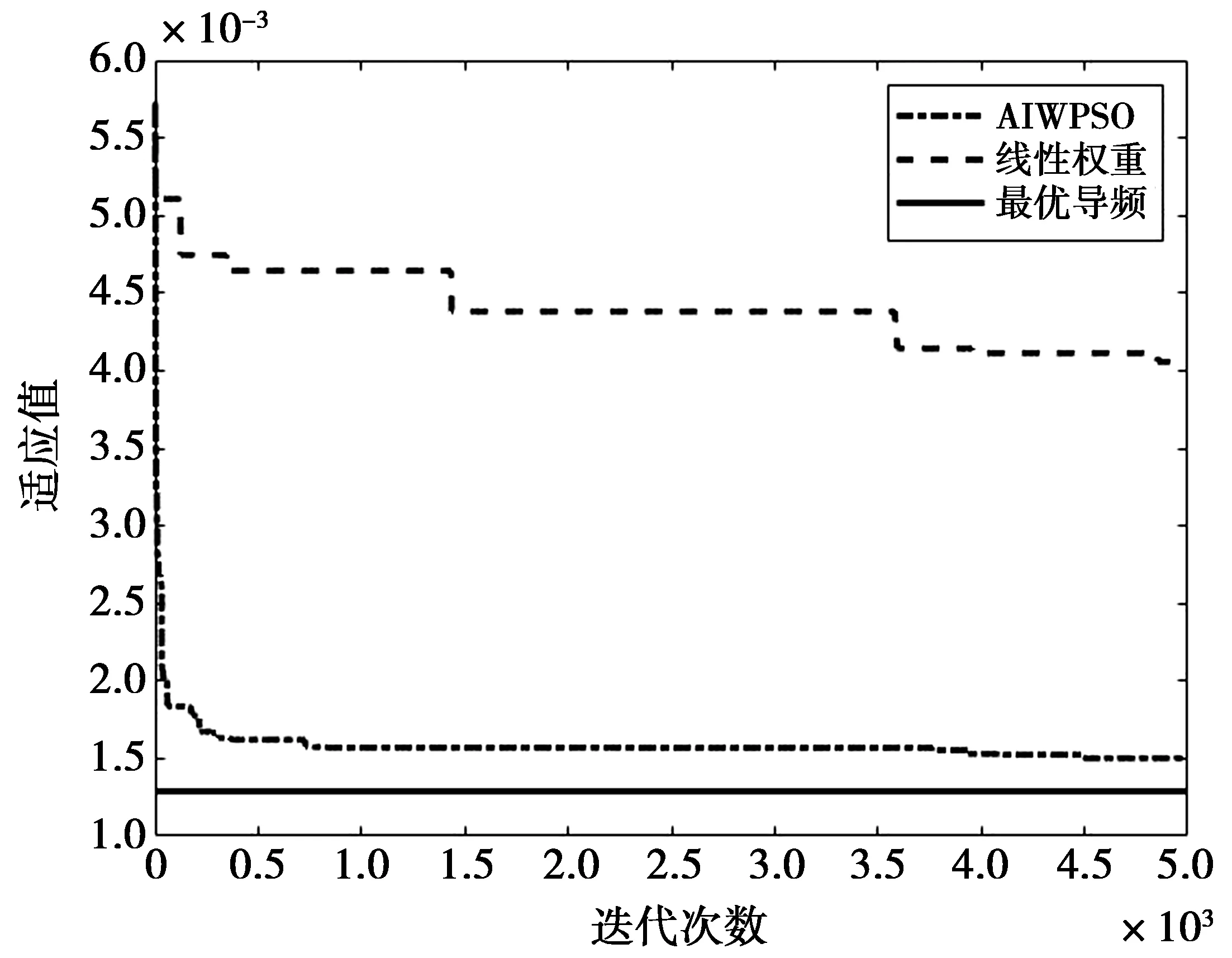
图4 多干扰频带进化曲线Fig.4 Evolution curve of multiple interference band

下面对几种算法的MSE性能进行对比仿真，其中，非导频点信道估计函数采用样条插值法得到，结果如图5、图6。MSE为可用频点处的估计误差进行5 000次Monte Carlo仿真求平均得到。由图5可知，自适应粒子群算法所设计的导频MSE性能远好于文献[9]所提出的等间隔等功率导频设计，接近于穷搜索算法的最优导频序列，并且在单干扰环境下性能接近于MSE理论最低值。在图6的多干扰环境下，自适应粒子群算法所设计的导频和最优导频的MSE较理想值有所增加，原因是此时不可用频带长度增加，插值函数误差加大，而等间隔等功率导频MSE性能下降明显，较本文算法在均方误差为10-2时信噪比损失约12 dB。

图5 单干扰频带MSE比较Fig.5 Single interference band MSE comparison

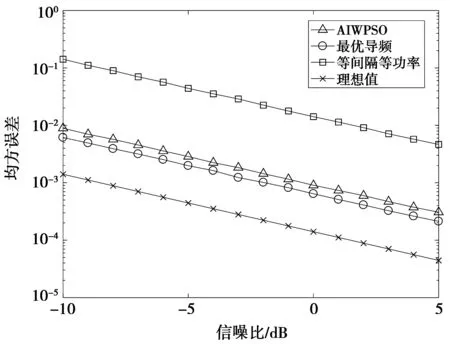
图6 多干扰频带MSE比较Fig.6 Multiple interference band MSE comparison

4.2 TDCS性能验证

TDCS具有良好的低截获和低检测性能，源于其时域基函数的类噪声特性，而高斯白噪声服从正态分布，下面通过仿真基函数概率分布曲线验证导频插入对TDCS类噪声性能的影响，结果如图7、图8。可以看出，不论在单干扰环境和多干扰环境下，导频插入基函数的概率分布曲线都能沿其正态分布基准线出现，其误差与原始基函数基本保持一致，可以认为采用导频辅助的信道估计对TDCS基函数的类噪声特性基本不产生影响。

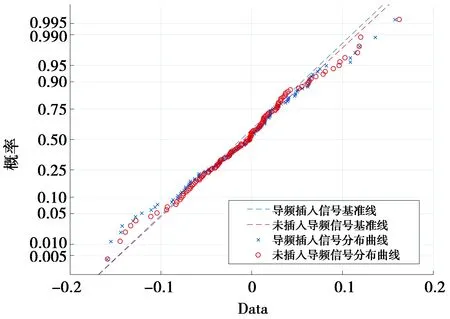
图7 单干扰频带基函数概率分布图Fig.7 Probability distribution of basic function in single interference band

图8 多干扰频带基函数概率分布图Fig.8 Probability distribution of basic function in multiple interference band

下面从误码率(bit error rate, BER)角度导频序列在低信噪比环境下的TDCS通信性能，对基函数进行2阶CCSK调制，发送数据独立同分布等概率产生。图9、图10分别比较了3种算法在单干扰频带和多干扰频带环境下的BER性能。可以看出,在2种干扰环境下等间隔等功率设计的BER均较高，而自适应粒子群算法在避免穷尽搜索最优导频的同时，采用了DSMSE为进化函数，在2种干扰环境下的BER性能远远优于等间隔等功率设计，并且接近于最优导频序列。在BER为0.2时，自适应粒子群算法所设计的导频较等间隔等功率导频在单干扰和多干扰频带下分别有2.6 dB和2.2 dB的性能增益，与最优导频序列信噪比相差小于0.7 dB。

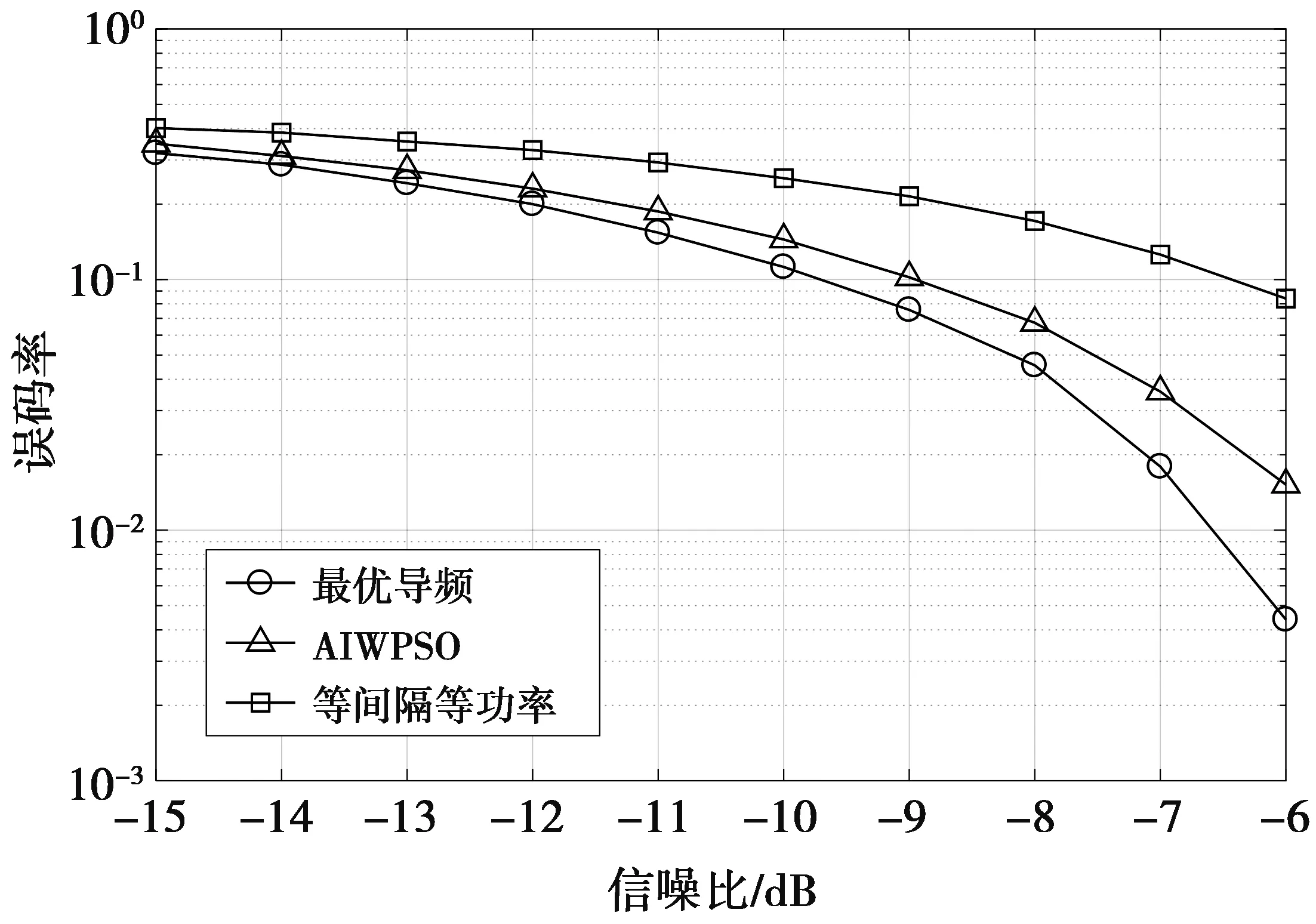
图9 单干扰频带BER比较Fig.9 Single interference band BER comparison

图10 多干扰频带BER比较Fig.10 Multiple interference band BER comparison

5 结 论

在详细分析TDCS基函数特点和最小二乘法信道估计性能的基础上，提出了一种适合TDCS的自适应粒子群导频优化算法。针对MSE准则无法准确描述导频优化方向的问题，设计DSMSE作为导频优化的目标函数，最大程度降低了信号畸变产生的误码率损失，并针对粒子群算法收敛慢，容易陷入局部最优的问题，设计了自适应惯性权重，提升导频优化能力，最后构建导频优化模型并对导频的位置和功率进行联合优化。仿真结果表明，自适应粒子群导频优化算法在单干扰和多干扰频带环境下均能保持较快的收敛速度和较强的导频优化能力，其信道估计精度更接近于最优导频序列，误码率结果表明新算法有效降低了传输信道给系统造成的误码率损失，适用于复杂干扰环境下的TDCS信道估计问题，对提升TDCS在多径信道中的通信能力具有重要意义。