Stationary response of colored noise excited vibro-impact system∗

Jian-Long Wang(王剑龙), Xiao-Lei Leng(冷小磊), and Xian-Bin Liu(刘先斌)

State Key Laboratory of Mechanics and Control of Mechanical Structure,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

Keywords: vibro-impact system,stationary probability density function,stochastic averaging method,generalized cell mapping method

1. Introduction

The vibro-impact system is an essential kind of non-linear dynamic system,which has attracted considerable attention in the past few decades.[1–6]Owing to its non-smooth characteristics,some interesting and distinguishing phenomena such as gazing bifurcation,tour bifurcation,chatter,and sticking motions are observed in the deterministic system.[7–12]In terms of stochastic dynamics, efforts are made to derive the stationary response of the vibro-impact system under the excitation of various noises. The most common ways are the stochastic averaging method and path integration method.[13–15]Huang[16]developed a stochastic averaging method to obtain the stationary response of a multi-degree-freedom vibro-impact system under the white Gaussian noise excitation. Recently, a solution procedure consisting of Zhuravlev non-smooth transformation and exponential polynomial closure method has been proposed to obtain the probability density function(PDF)of a lightly vibro-impact system excited by different white Gaussian noises.[16]In Ref. [17], the path integration was greatly simplified to accurately obtain the stationary response by introducing a suitable transformation of the state space to deal with the vibration systems’ discontinuities with strong inelastic impact. More recently, an iterative weighted residual method was employed to obtain the approximate closed-form solution of the random response of a single-degree-freedom vibro-impact system under the white Gaussian noise.[18]More recent efforts dedicated to the vibro-impact system’s stationary responses under various random excitations are available in Refs.[19–27].

For the stochastic averaging method, one important step is to transfer the physical process to the Ito diffusion process.Because the existing theory can only obtain the accurate drift coefficient and diffusion coefficient for the system under the physical white noise or the wide-band noise,the application of the stochastic averaging method is limited.[28]It can be seen that almost all the excitations in the above researches are in white or wide-band. However, in nature, the real noises always have a finite correlation time. When the noises’correlation time is considerably long,there are no effective methods to obtain the stationary response.

In recent years, the stochastic GCM method has been wildly used to obtain the response PDFs for systems subjected to white excitations.[29–36]In this paper, based on the Khasminskii limit theorem, the GCM method is improved to obtain the stationary response of a vibro-impact system under a colored noise excitation. Owing to no need to obtain the precise drift coefficient or diffusion coefficient of the approximated Markov process but the process’s evolution law, the GCM method can be applied to both the wide-band noise excited system and the narrow-band noise excited system.

The rest of the paper is organized as follows.In Section 2,the model of the vibro-impact system is described. The procedure of the stochastic averaging method for the system is presented in Section 3. In Section 4,the GCM method for the white noise excited system is introduced,and its applicability to the colored noise excited system is investigated. In Section 5, both the methods are tested for wide-band noise and narrow-band noise, and the results are verified by the Monte Carlo simulation. Finally, the conclusions are summarized in Section 6.

2. Vibro-impact system

Vibro-impact systems are encountered in many engineering applications such as structures and machines with rigid barriers,clearance,and gaps. Therefore,it is essential to study the dynamics of the vibro-impact system. Here we consider a vibro-impact system with a clearance type nonlinearity as shown in Fig. 1. The motion equation of the system is given as[37]

wherexis the system displacement and overhead dot denotes differentiation with respect to timet;ζis the linear damping coefficient;kis the linear stiffness;blis the distance between the equilibrium position of the mass and the lift barrier;bris for the right barrier;Fis the contact force governed by Hertz contact model when the mass crashes to the barriers[38]and it is expressed as

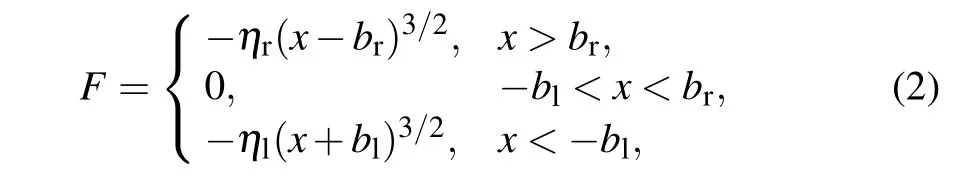
whereηlandηrrepresent contact stiffness between the mass and the barriers on both sides respectively,and they are dependent on their geometries and material properties;the excitationfin Eq. (1) is assumed to represent a stationary and ergodic process,which is generated by a white noise passing through a second-order linear filter,and it satisfies the following equation:

LetS(ω)be the rational spectral density and can be presented as

whereζ1,ω1, andDare constants, and they determine the bandwidth of the noise;W(t) is a standard white Gaussian noise,which can be either a wide-band noise or a narrow-band noise.

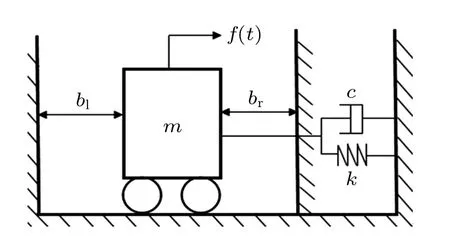
Fig.1. Schematic model of vibro-impact oscillator.

Combining the contact forceFwith the spring forcekx,equation(1)can be rewritten as

whereg(x)is a restoring force of the system and it is expressed as

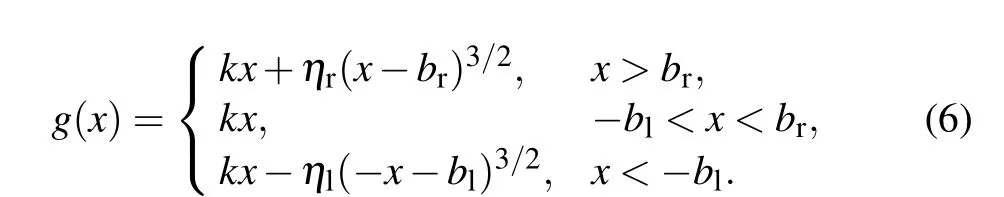
The potential energy function and the total energy function of the system can be obtained as

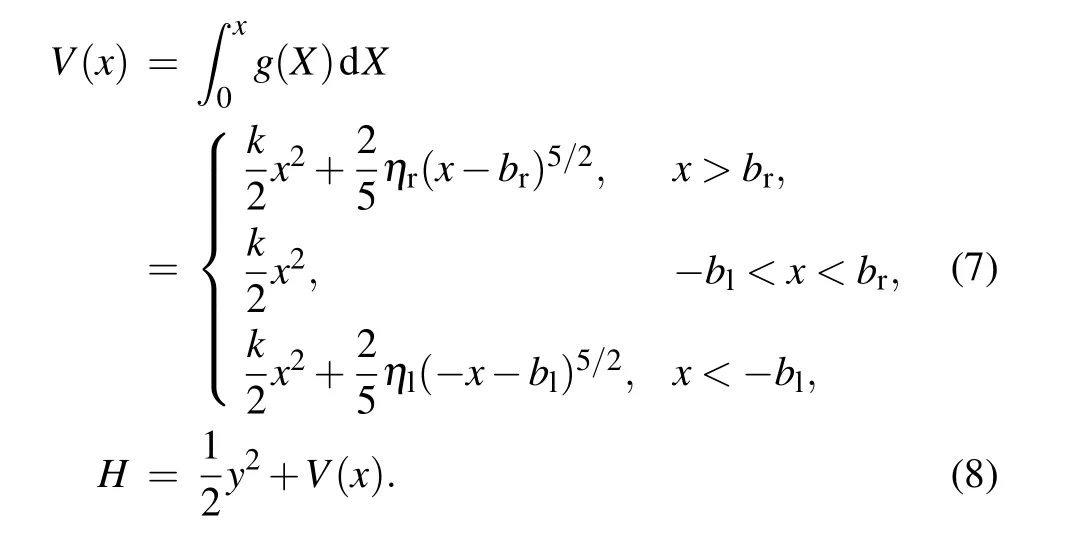
3. Stochastic averaging method

In this section, the stochastic averaging method is conducted to obtain the stationary responses of the system.Before moving on, it should be noted that equation (5) is a strongly nonlinear oscillator and does not meet the requirement of the stochastic averaging method. According to Ref.[39],the generalized harmonic transformation should be used to modify the system into a correct form.

Assuming that the damping coefficient is slight and the external random excitation is weak, the motion of Eq. (5) is nearly periodic and can be written as

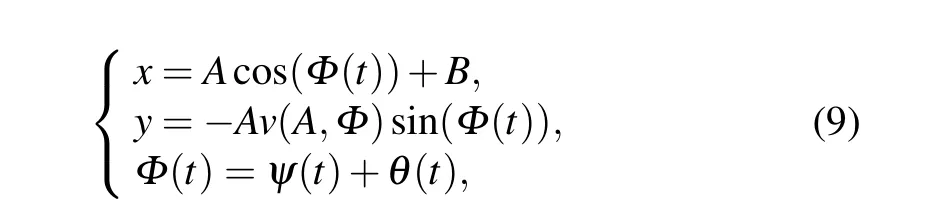
where

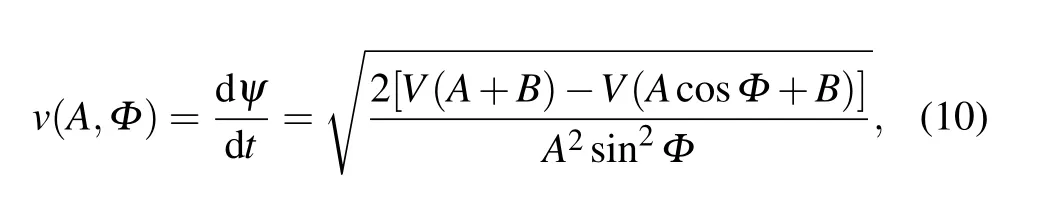
withBbeing a deviation process,Aan amplitude process,Φ,ψ, andθthe phase processes, andvthe instantaneous frequency of the oscillator.AandBare related toHby

Transform the variable fromxandyintoAandθrespectively,then equation(5)will become

where

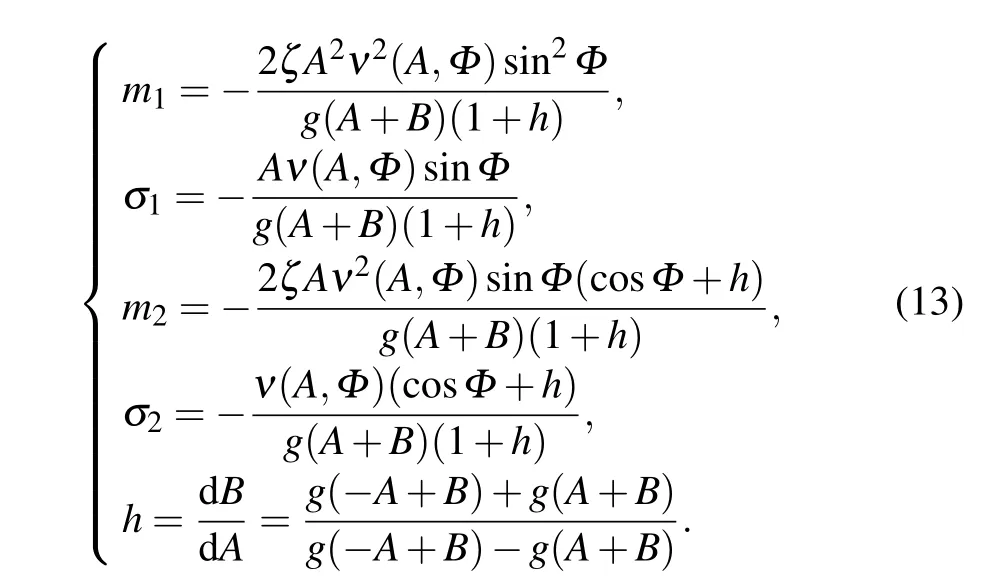
On the assumption that the damping coefficient is slight and the random excitation is weak, the terms on the righthand side of transformed equation (12) are indeed small;hence,the transformed equation(12)is a standard form for the Stratonovich–Khasminskii limit theorem,Aandθwill converge weakly to a two-dimensional diffusive Markov process asζ,D →0. Furthermore, when the random excitation is in the wide-band,the Markov process can be represented by the following Ito stochastic differential function

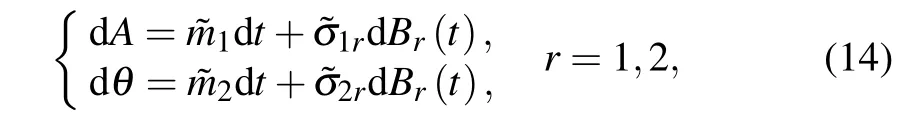
whereBr(t) represents the standard Wiener process.iandij=irjrare called drift coefficient and diffusion coefficient, respectively. They can be obtained from the following formula:

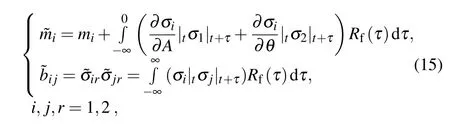
whereRfis the correlation function of the random noise.

Considering the fact that theAandθare the slowly varying variables, the drift and diffusion coefficient in Eq. (14)can be smoothened by time-averaging. Denoting the timeaveraged drift and diffusion coefficient by

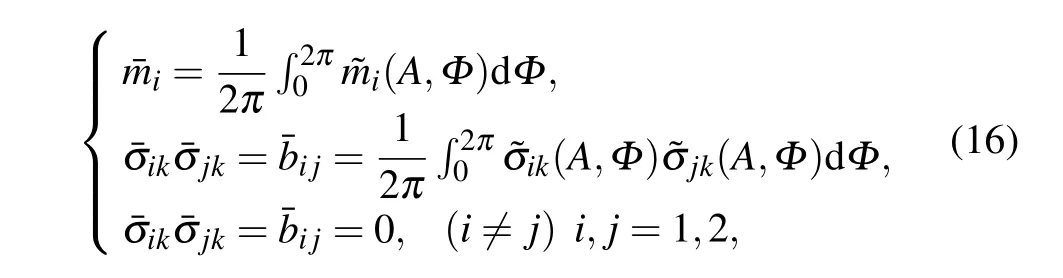
the Ito equation becomes

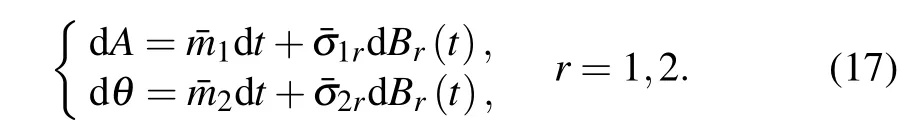
It can be seen that the smoothedAprocess becomes independent ofθ. Hence it can be presented by the following onedimensional Ito equation:

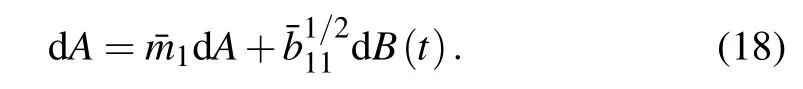
The associated FPK equation has the form

wherep=p(A,t|A0)is the transition probability density ofAwith the initial condition

Assuming that the boundary conditionpatA=0 is finite,and

the stationary solution of FPK equation can be derived analytically as

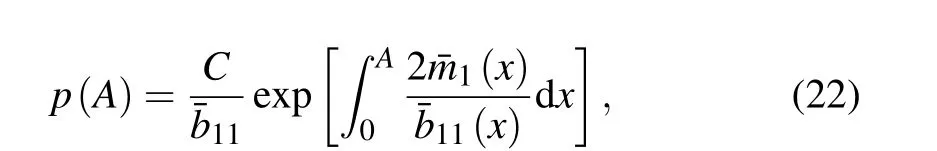
whereCis the normalization constant.

As the stationaryp(A) is solved, the stationary PDF of the total energyp(H)can be derived fromp(A)as

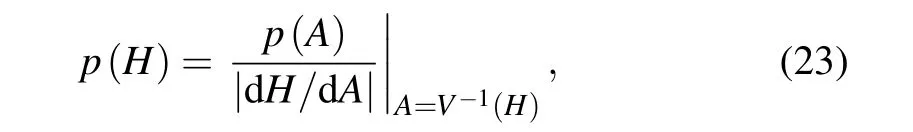
whereA=V−1(H) is the inverse function ofH=V(A+B(A)).

The stationary joint PDF of displacement and velocity can be further obtained as

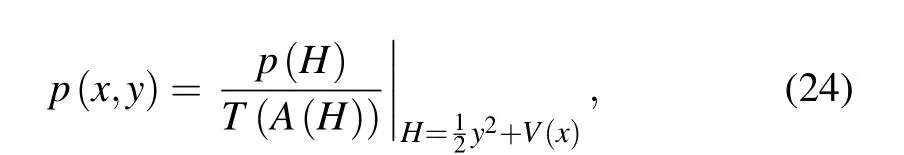
whereTis the instantaneous period of the system and expressed as

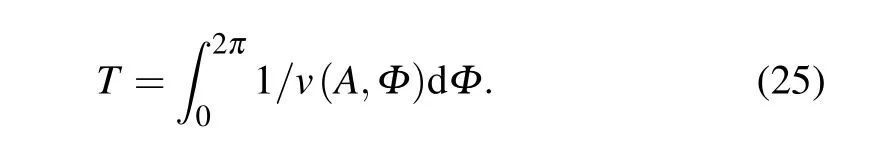
The stationary PDFs of displacement and velocity can be expressed as

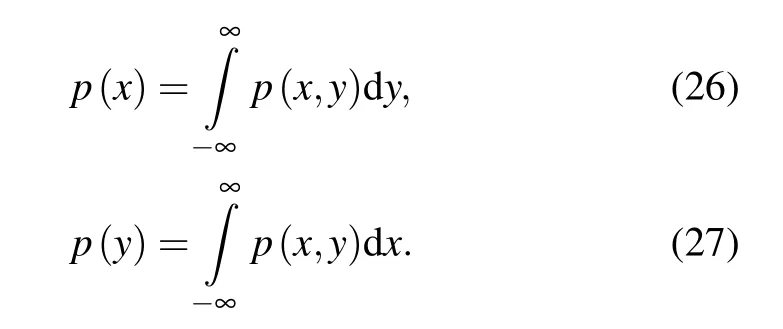
Finally, it is mentioned that as the stochastic averaging method isoperated,v,mi,andσiin Eqs.(10)and(13)are usually approximated by only the first 6 terms of the Fourier series to simplify the computation procedure with a relative error of less than 0.03%[39]

4. Generalized cell mapping method

In recent years,the stochastic GCM method is greatly developed to obtain the response PDFs for systems subjected to random excitations.[29–36]Compared with the traditional numerical methods, the GCM can greatly reduce the simulation time and achieve a very accurate result. However, the application of the GCM method requires the response process of the random excited system to be a Markov process. Hence its application is limited only to the white noise excited system.So far,no work has been done on the applicability of the GCM method to the colored noise excited system.

In this section,we introduce the GCM method for the systems subjected to the white noise, then the possibility of extending the GCM method to our colored noise excited vibroimpact system is investigated.

4.1. GCM for system with white noise

First, we give the theoretical mechanism for the GCM method. As is well known, the responsex=(x,y) in Eq. (5)will form a Markov process if the excitationfis a white noise.Therefore according to the Markov property, for any finite value 0≤t1＜t2＜···＜tn,the following equations hold

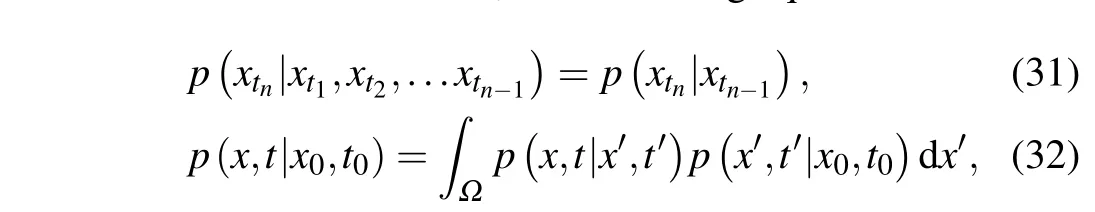
wheret0≤t＇≤t,Ωis the state space forx. Dividing the interval[t,t0]intonsubintervalt0＜t1＜···＜tn=t,equation(32)can be rewritten as

Note that equation (5) is the time-homogenousp(xn,tn|xn−1,tn−1)=p(xn,tn −tn−1|xn−1,0)andti−ti−1=∆t,∀i ∈1,...,n. Then the PDFp(x,t) at any timetcan be obtained as

Now, we give the detailed procedure of operating the GCM method. First, we discretize the continuous state spaceDintoNsmall cellsCi(i=1,2,...,N)as shown in Fig.2. Letpi(n)denote the probability of the cellCiatn-th step in steps of mapping length ∆t, andpij, the one-step transition probability from cellCjto cellCiis

Then the probability evolution of the system can be described by a homogeneous Markov chain

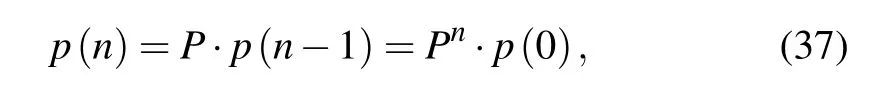
wherep(0) denotes the initial probability distribution andPis the one-step transition probability matrix with elementspij.Thus,once the one-step transition probability matrixPand the initial probability distributionp(0)are given,the transient and the stationary PDF can be computed.

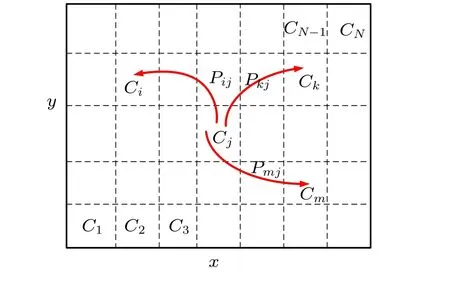
Fig.2. Schematic diagram for GCM method.

Finally, we takepijfor example to show how to obtain the matrixPby using the GCM method. First,Qjinner points are uniformly selected in the cellCjandsrandom sample trajectories are generated from each point. In this manner,there are totalS=sQjtrajectories constructed in the cellCj.It is assumed that there areSitrajectories of time duration ∆tfalling into cellCi, then the one-step transition probability from cellCjto cellCican be calculated frompij=Si/S.

4.2. GCM for colored noise excited system

The method mentioned above is based on the fact that the response process under white noise is a homogenous Markov process. Hence, equation (31) is always tenable whatever∆t=tn −tn−1is chosen. However, when the excitation is a colored noise in our system,the response process of Eq.(5)is no longer a Markov process. Therefore,will the GCM method not be applicable to our system anymore? The following analysis will indicate that the answer is yes.

For the systems having the following form:

where thefjandgjrare deterministic functions andξrare stationary random excitations with zero means,the Khasminskii limit theorem[40]shows that the processX(t) will converge weakly to a Markov diffusion process in a semi-infinite time interval asε →0. Furthermore, supposing thatX(t) is not observed continuously, but discretely, beginning fromtin time intervals of ∆t＇. Then, if the observation time interval ∆t＇≥τrs,whereτrsis the correlation time betweenξrandξs, the authors in Refs.[28,41]show that the observed incrementX(t+∆t＇)−X(t) between those time intervals will become independent.The stochastic averaging method is exactly based on this theory and uses the time-averaged first and second increment moments as the drift coefficient and diffusion coefficient as follows:[28]

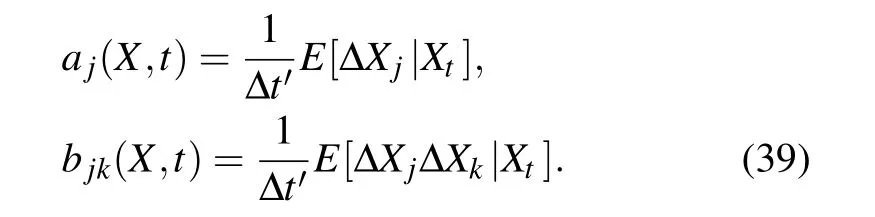
Especially when the noise is wide-band(τrs≪1),the observation time interval can be chosen as 0＜τrs＜∆t＇ ≪1;in this short interval, the variation of thefjandgjrare very slight, the drift coefficient and the diffusion coefficient of the diffusion process can be given accurately as[28]

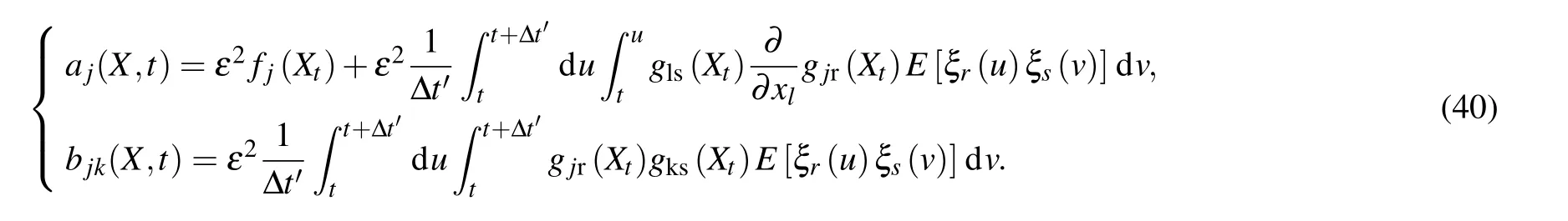
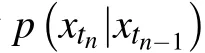
5. Examples

In this section,both the Stochastic averaging method and the generalized cell mapping method are tested by using concrete examples, and the MC simulation is conducted to validate their effectiveness.

The system parameters are given asζ=0.1,k=1,ηl=ηr=80,bl=0.2, andbr=0.1. In the first case, the noise’s parameters are chosen asζ1=0.6,ω1=6,andD=0.4. With such specified parameters,the excitation is in wide band. The excitation’s correlation function is shown in Fig. 3. It can be seen that when the absolute value of the time differenceτis greater than 2 s,the two forcesf(t)andf(t+τ)become uncorrelatedE[f(t)f(t+τ)]≈0.

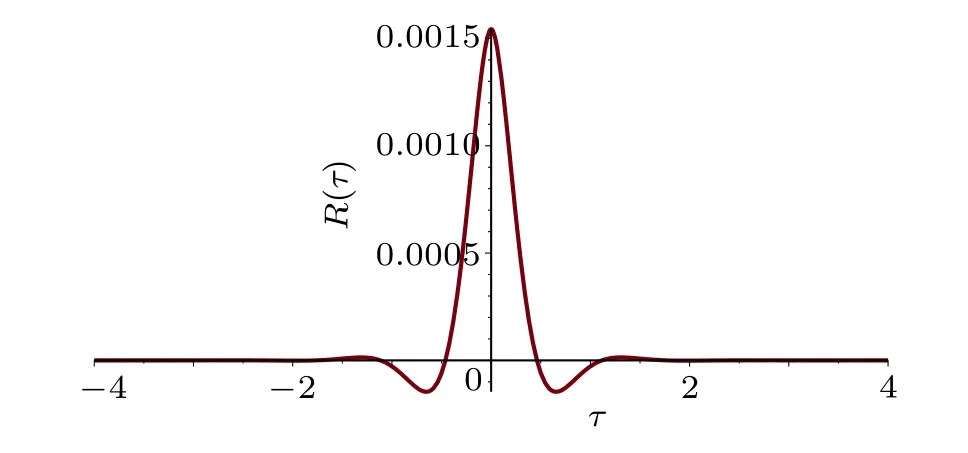
Fig.3. Correlation function of excitation f.

The concrete steps of the GCM method are given as follows. First, we choose the domain of interest,Z={−0.4＜x ＜0.4,−0.4＜y ＜0.4}, in the state space and divide the domainZinto 80×80 cells. After that, 5×5 interior points are uniformly selected within each cell,and 1000 sample trajectories with the time duration ∆tare generated from each of these points. Hence,the one-step transition probability matrixPis constructed by the total 2.5×104sample trajectories in each cell. The initial probability is assumed to be a uniform distribution, then the stationary PDF of the response process can be computed according to Eq.(37).

The stationary PDFs of amplitude,total energy,displacement,and velocity derived by the stochastic averaging method are shown in Fig. 4 with the solid lines; those of the GCM method with different one-step mapping times are shown with dot-dash lines. From Fig. 4, we can see that the results obtained by the averaging method agree well with those from the MC simulation method. Meanwhile, the results of the GCM method gradually converge to those of the averaging method as the one-step mapping time ∆tincreases. When ∆tis chosen to be greater than 5 s,it is sufficient to have a good result with a high accuracy.The joint probability densities of velocity and displacement shown in Fig.5 are also in good agreement with the results from all the methods.

Now,we choose another set of noise parametersζ1=0.6,ω1=0.5,D=0.0005, andD=0.002. The low frequencyω1=0.5 in Eq. (3) ensures that the noise is a narrow-band noise, while the smallDensures that the noise is weak. The excitation’s correlation function is shown in Fig.6,and when the time differenceτis greater than 20 s,E[f(t)f(t+τ)]≈0.Hence, when the GCM method is applied, the one-step mapping time ∆tmust be chosen to be greater than 20 s,and here we chose ∆t=30 s.

The stationary PDFs of amplitude,total energy,displacement, and velocity derived by both the stochastic averaging method and the GCM method are shown in Fig. 7. In this case, the stochastic averaging method is not valid anymore.The reason is that as the correlation time of the noise increases,the observation time gap should also be increased,leading the drift coefficient and diffusion coefficient of the Markov diffusion process l not to be in the form of Eq. (40) anymore. In contrast, since the GCM method does not need to calculate those specific quantities but only to obtain the evolution law of the process,it can still predict the results well.

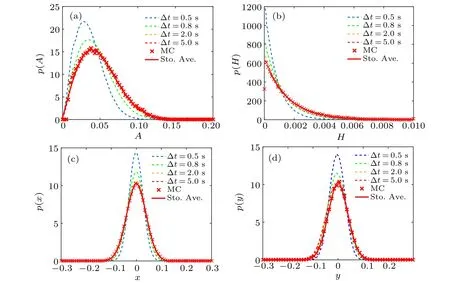
Fig.4. Stationary probability densities: (a)amplitude,(b)total energy,(c)displacement,and(d)velocity. (dash line: stochastic averaging; solid line:generalized cell mapping;Cross×: Monte Carlo simulation).

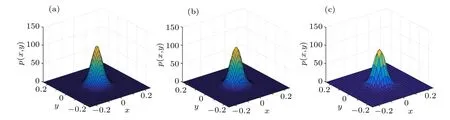
Fig.5. Joint probability density of velocity and displacement(a)stochastic averaging,(b)generalized cell mapping with ∆t=5 s,and(c)Monte Carlo simulation.

Fig.6. Correlation function of the excitation f for(a)D=0.0005 and(b)0.002.

Fig. 7. Probability densities (red, D=0.0005; black, D=0.002): (a) amplitude, (b) total energy, (c) displacement, (d) velocity. The dash line is stochastic averaging;solid line is generalized cell mapping ∆t=30 s;cross×: Monte Carlo simulation.

6. Conclusions

Based on the Hertz impact model, the response of a single-degree-of-freedom vibro-impact system under the random colored noise is investigated. First,the stochastic averaging method is carried out routinely. Then the GCM method,which is theoretically only applicable to the Markov process,is also tried for this colored noise excited system. The results show that if the one-step mapping time is chosen to be greater than the correlation time of the noise, the probability evolution of the system can be approximated by the onestep transition probability matrix. The application examples show that the GCM method can well predict the results no matter whether the noise is wide-band or narrow-band, while the stochastic averaging method is valid only for the wideband noise. Hence, the GCM method’s application is greatly extended.It is no longer limited to the white noise excited system,but still to the colored noise excited system. On the other hand,due to the successful prediction of the GCM method,if we accurately work out the drift coefficient and diffusion coefficient of the approximated Markov process,the application of the stochastic averaging method to a narrow-band noise excited system still seems possible.