Quantum computation and error correction based on continuous variable cluster states∗

Shuhong Hao(郝树宏) Xiaowei Deng(邓晓玮) Yang Liu(刘阳) Xiaolong Su(苏晓龙)Changde Xie(谢常德) and Kunchi Peng(彭堃墀)

1State Key Laboratory of Quantum Optics and Quantum Optics Devices,Collaborative Innovation Center of Extreme Optics,Institute of Opto-Electronics,Shanxi University,Taiyuan 030006,China

2School of Mathematics and Physics,Anhui University of Technology,Maanshan 243000,China

3Shenzhen Institute for Quantum Science and Engineering,Southern University of Science and Technology,Shenzhen 518055,China

Keywords: quantum computation,quantum error correction,continuous variables,cluster state

1. Introduction

Quantum computation (QC) provides an exponential speedup over classical computing for certain problems, such as integer factoring[1]and quantum simulation.[2]Recently,quantum computation with several systems, such as superconducting systems,[3–5]ion trap systems,[6]and silicon-based systems,[7]has made enormous progress. Generally,there are two kinds of QC models, one is the traditional circuit model,in which unitary evolution and coherent control of individual qubits are required,[8]the other one is the measurement-based QC model,[9]which is also named one-way QC since computation is implemented by performing measurement and feedforward of measurement results on a large scale cluster state.The measurement-based QC is scalable and provides the ability to perform universal QC using only single-qubit projective measurement, given a specially prepared and highly entangled cluster state.[9,10]In the measurement-based QC, the resources required for QC using linear optics can be significantly reduced by first creating photonic cluster states via nondeterministic gates.[10]Essential progress has been made for measurement-based QC, such as measurement-based QC with a four-qubit cluster state of single photons[11–13]and measurement-based quantum computation with trapped ions system.[14]

To build a quantum computer, seven stages are involved,[15]which are (1) operations on single physical qubits, (2) algorithms on multiple physical qubits, (3) quantum nondemolition(QND)measurements for error correction and control,(4)logical memory with longer lifetime than that of physical qubits,(5)operations on single logical qubits,(6)algorithms on multiple logical qubits, and (7) fault-tolerant quantum computation. These stages are divided according to the complexity of the task and different technologies are required at each stage. At present, the third stage has been attained by trapped ions[16]and superconducting system,[17]respectively. The fourth stage, where a logical qubit can be stored,via error correction,for a time substantially longer than the decoherence time of its physical qubit components,has not been reached. Recently,quantum states on 53 qubits were created using a programmable superconducting process[18]and Gaussian boson sampling was demonstrated using 50 singlemode squeezed states.[19]

For quantum information based on optical systems,there are two different systems, which are discrete variable (DV)and continuous variable (CV) systems, respectively. Quantum variables defined in finite and infinite Hilbert spaces are used in DV and CV systems, respectively. Optical quantum information with DV and CV systems are developing in parallel and have their own advantages and disadvantages. The DV system encodes information on discrete variables, such as polarization of photons. For the DV optical system, the maximal entanglement can be obtained but the generation of entanglement is probabilistic usually. While for the CV optical system, which always encodes information on the amplitude and phase quadratures(corresponding to position and momentum,respectively)of an optical field,the generation of entanglement is deterministic but the perfect entanglement is not able to be obtained.[20,21]So far,tremendous progress has been achieved for optical quantum networks with DV and CV systems.

Cluster state is the basic resource for measurement-based QC. There has been remarkable achievement in the preparation of CV cluster state, from four-mode[22–24]to eightmode,[25]60-mode in frequency comb,[26]10000-mode,[27]one million modes,[28]and two-dimensional one in time domain.[29,30]The successful preparation of large scale CV cluster state makes it possible to realize the measurementbased QC with CV cluster state. Measurement-based QC with CV cluster states provides a feasible way for scalable quantum information processing.[9,10]It can be realized by measurement and classical feedforward on a Gaussian cluster state,which is prepared deterministically.[21,31,32]Firstly, a quantum nondemolition sum gate and a quadratic phase gate for measurement-based CV QC were demonstrated based on utilizing squeezed states of light in 2008 and 2009,respectively.[33,34]Successively,a controlled-Xgate based on a four-mode CV cluster state was presented,in which a pair of quantum teleportation elements were used for the transformation of quantum states from the input target and control states to the output states.[35]Later,the squeezing operation,Fourier transformation,and controlled-phase gate were also achieved,in which a four-mode optical cluster states served as the resource quantum states.[36,37]Currently,several quantum logical gates in CV QC have been demonstrated, but the realization of an algorithm remains a challenge.

In the practical QC, the inevitable interaction between the quantum state and environment will lead to errors. Thus,quantum error correction (QEC) is a necessary procedure to protect quantum state against errors. The essential idea in QEC is to encode information in subsystems of a larger physical space that are immune to noise.[3]In QEC, physical qubits are encoded as QEC code, which is used to identify errors and correct the corresponding errors. In faulttolerant QC, logical qubits are encoded within the errorcorrected system of physical qubits and are used to implement quantum algorithms.[3]In recent years,proof-of-principle experiments have been demonstrated in various experimental systems.[16,17,38–41]Fault-tolerant QC,which implements QC by encoding quantum states in a QEC code, enables one to build a quantum computer which behaves correctly in the presence of errors.[42,43]Fault-tolerant measurement-based QC with CV cluster states is possible with finite squeezed cluster states above a threshold value by concatenating with quantum stabilizer codes and some special ancilla-based quantum code such as Gottesman–Kitaev–Preskill(GKP)code.[44]

In this paper, we briefly introduce the progress of CV measurement-based QC. In Section 2, the progress of Gaussian cluster state, the theoretical principle of measurementbased CV QC, the experimental details of the related techniques,and the applications of some CV quantum logical gates are introduced. In Section 3, we introduce the progress of CV quantum simulation. In Section 4, the progress of CV QEC,the fault-torrent measurement-based quantum computation with two classes of QEC codes and the recent progress of the experiment techniques are introduced. Finally,we discuss the challenges toward fault-tolerant CV QC.

2. Measurement-based CV QC

2.1. The CV cluster state

Cluster state, which is a type of multipartite entangled state with next-neighbor interactions (Ising type interactions),[32,45]is the basic resource for measurementbased QC[9,10]and quantum network.[46,47]In CV QC, the quantum variables are the amplitude and phase quadratures of the quantum electromagnetic field described as, which satisfies the usual bosonic commutator [,†]=1. When the convention=1/2 is chosen,its amplitude and phase quadratures can be expressed asrespectively. The variance of the vacuum state is given byσ()2=σ()2=1/4. Generally, CV cluster states are defined as

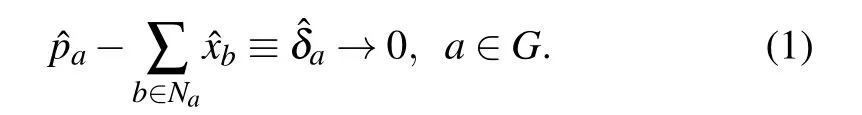
The modesa ∈Gdenote the vertices of the graphG,while the modesb ∈Naare the next-neighbors of modefor ideal case,the excess noiseatends to be zero.

As shown in Fig.1,each node in a cluster state represents a qubit or qumode, the edge represents the next-neighbor interaction between the neighboring nodes.[32]It is obvious that the cluster state can protect entanglement property since when a measurement is performed on one qubit or qumode only the interaction next to this qubit is destroyed, while the entanglement of other qubits not next to the measured qubit still exists.[48]Based on this entanglement persistence property,the cluster state is a naturally good resource for measurementbased QC.[9,10]

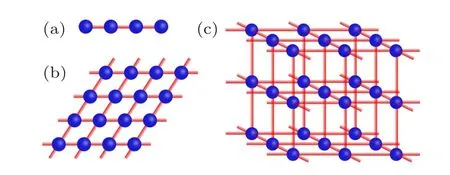
Fig.1. Examples of cluster states. (a)A linear four-mode cluster state.(b) A two-dimensional cluster state. (c) A three-dimensional cluster state.

There are mainly three types of experimentally prepared CV cluster states,which are space-separated,frequencydomain, and time-domain cluster states, respectively. These three types of CV cluster states are developing in parallel and have their own advantages and disadvantages. To prepare the space-separated CV cluster state, a linear optical transformation of squeezed states on a specially designed beam-splitter network is used.[22–25]The advantage of the space-separated cluster state is that local operations can be easily applied to each qumode. The drawback of this method is that with increasing of the entangled modes the complexity of the experimental setup is also subsequently increased. Using this method,space-separated four-mode and eight-mode CV cluster states were prepared experimentally[22–25]and applied in CV QC,respectively.

To prepare the CV cluster state in frequency domain,the technique of the optical frequency comb is applied,with which the lager scale cluster states can be prepared in principle.[49]In 2014, Chenet al.experimentally realized one 60-mode copy and of two 30-mode copies of a dual-rail quantum-wire cluster state in the quantum optical frequency comb of a bimodally pumped optical parametric oscillator.[26]In 2017,Caiet al.realized the construction of thirteen cluster states by measuring a frequency comb with appropriate pulse shaped local oscillator,which was obtained by a computer-programmed spatial light modulator.[50]However, in this way, these entangled modes are not easily separated and thus the schemes of utilizing them to implement QC need to be redesigned.

To prepare the CV cluster state in time domain, two squeezed light beams are divided into time bins and are coupled on a balanced beamsplitter.[27]Then one output mode from the balanced beamsplitter is delayed through a fibre delay line. Finally, by combining the staggered states on the second balanced beamsplitter, a cluster state in time domain can be generated.[27]In 2016,Yoshikawaet al. demonstrated the successive generation of fully inseparable light modes for more than one million modes.[28]Remarkably, in 2019, twodimensional cluster states were experimentally prepared by Furusawa’s group and Anderson’s group, respectively.[29,30]Very recently, a method to generate CV three-dimensional cluster state in time domain was proposed for topologicallyprotected measurement-based QC.[51]It has been shown that such a three-dimensional cluster state is robust against analog errors derived from the finite squeezing during topologically protected measurement-based QC.as[10,53–55]

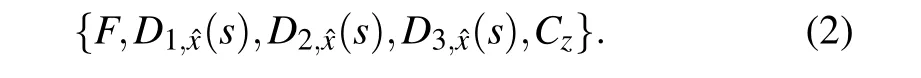
2.2. The CV measurement-based QC

The CV measurement-based QC is based on the cluster entangled state, which can be built by implementing an appropriate unitary transformation on a series of input squeezing state.[52]The elementary gate set which is sufficient for universal CV QC of arbitrary multi-qumode can be chosen

In 2011, Ukaiet al. demonstrated the complete set of one-mode linear unitary Bogoliubov(LUBO)transformations for continuous variables using a four-mode cluster state.[56]The fidelity obtained in the experiment was 0.68, which was limited by the squeezing level of the ancillary cluster state. In 2014, Haoet al.experimentally realized singlemode squeezing and Fourier transformation operations by using an Einstein–Podolsky–Rosen (EPR) entangled state as the resource.[58]The fidelity of the squeezing operation was 0.65 for 4 dB squeezing operation, which was limited by the squeezing level of the EPR entangled state. In 2016, Marshallet al.experimentally demonstrated the CV QC on encrypted data with Gaussian displacement and squeezing operations which can protect the security of a user’s privacy.[59]The fidelity was＞97% for losses of up to 10 km. In 2017,a scheme to realize a general single-mode Gaussian operation based on an EPR entangled state was proposed[60]and it has been shown that the classical Hadamard transform algorithm can be implemented with CV cluster state.[61]In 2020, Zhaoet al.proposed and experimentally demonstrated a heralded squeezing gate which achieved near unit fidelity for coherent inputs while requiring only modest ancillary squeezing and post-selection filter.[62]

2.3. Experimental realization of the logical gates for CV QC

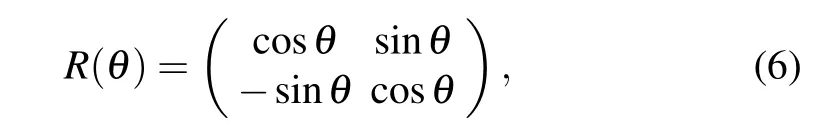
can be considered as the control of the phase of the input state.So we can lock the relative phase between two optical beams to implement the rotation operation. Fourier transform is the special case of rotation operation whenθ=π/2.

Fig. 3. The schematic of experimental setup of a squeezing gate. The sum(+)and difference(−)of the photocurrents measured by two homodyne detectors (HD1 and HD2) are fedforward to mode 2. The output mode is measured by HD3. EOMx and EOMp are the amplitude and phase electro-optical modulators. 1%R is a mirror with a 1%reflection coefficient. Revised from Fig.1 in Ref.[58].

whereθ1andθ2are the measurement angles of HD1and HD2,respectively. Chooseθ2=θ1and feed forward the measurement results to the submode2,which is implemented by coupling the displaced coherent beam and submode2on a beam splitter with reflectivity of 1%. The output state is given by

whereGsis the gain factor in the feedforward circuit, which can be described as

Lis the transformation matrix of the squeezing gate

Comparing the matrixes ofLandS,we can see that the squeezing gate can be obtained when er=cotθ1and the squeezing parameterrdepends on the measurement angleθ1.

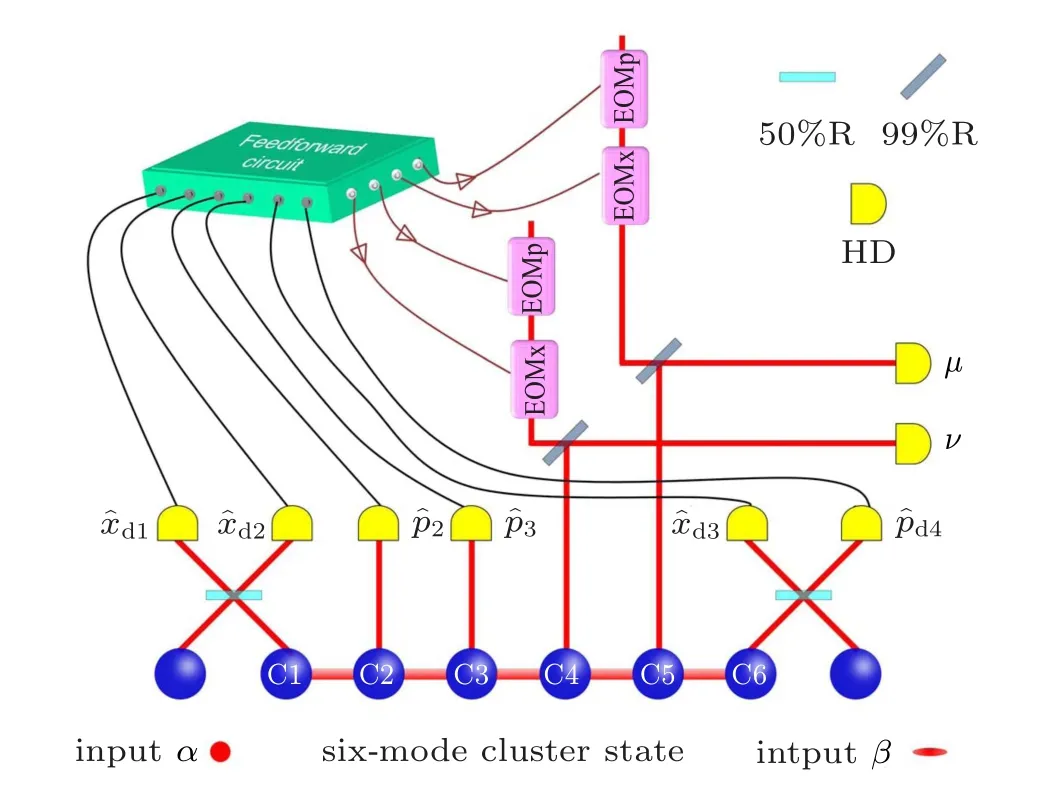
Fig.4. Schematic of experimental setup of the gate sequence. The input states α and β are coupled to a six-mode CV cluster state via two 50:50 beam-splitters,respectively. Measurement results from HD systems are fedforward to modes C4 and C5. The output modes µ and ν are measured by two HD systems. EOMx and EOMp: amplitude and phase EOM. 99%R, a mirror with 99% reflection coefficient. Revised from Fig.3 in Ref.[63].

As shown in Fig.4, the input modeα(target mode)and the other input modeβ(control mode) are coupled with the sub-mode C1 and C6 of the six-mode cluster state by 50:50 beam splitters, respectively. In the experiment, the amplitude and phase quadraturesd1,d2,d3,andd4of the output modes of two 50:50 beam splitters are measured by homodyne detectors, respectively, where the measurement anglesθ1andθ2in the homodyne detection ford1andd2determine the squeezing operation. The other two phase quadratures2and3coming from the sub-modesC2 andC3 of the six-mode cluster state are also measured. These measured results are fedforward to the amplitude and phase quadratures of modesC4 andC5 through classical feedforward circuits by using the amplitude and phase EOM,respectively. In this way,the squeezing gate on input modeαis performed firstly to produce a phase-squeezed state. Then aCZgate is performed on the output mode from the squeezing gate and the other input modeβcoming from outside of the sequence. The whole gate sequence is described as

is the transformation matrix of the gate sequence.i(i=1,2,...,6) are the corresponding excess noise terms for each mode of the CV six-mode linear cluster state. The quantum property of this gate sequence is confirmed by the fidelities and the quantum entanglement of the two output modes,which depend on both the squeezing and controlled-phase gates.[63]This experiment demonstrates the feasibility of implementing Gaussian quantum computation by means of accessible gate sequences.

2.4. Non-Gaussian gate for CV QC

Non-Gaussian gate is a key part in CV QC for exponential speedup to solve certain computational problems.[54]Bosonic operators of annihilationand creation†are essential non-Gaussian operations. The annihilation operation can be realized by transmitting the target state through a low reflectivity beam splitter. Once a single photon in the reflection channel is detected, it can be treated that the annihilation operation is conditionally realized.[64,65]Photon creation operation can also be conditionally achieved with the help of a low-amplitude spontaneous parametric down-conversion progress.[64,65]

It has been shown that in order to achieve arbitrary unitary operations for CV QC,it is essential to add a cubic gate to other Gaussian operations.[55]Gottesman,Kitaev,and Preskill proposed a scheme to realize a cubic gate with Gaussian operations, Gaussian measurement, quadratic feedforward, and an ancillary cubic state, which is based on the two-mode squeezed vacuum and photon number resolving detectors.[66]In 2011,Mareket al.proposed a scheme to achieve weak nonlinearity with single-mode squeezed vacuum state and photon subtraction or addition technique.[67]In 2015, Marshallet al.introduced a “repeat-until-success” approach to generate the cubic phase gate by using sequential photon subtractions and Gaussian operations.[68]In 2016,Miyataet al.presented the implementation of a quantum cubic gate by an adaptive non-Gaussian measurement which composed of a non-Gaussian ancillary state,linear optics,and adaptive heterodyne measurement.[69]In this scheme,the nonlinearity is generated by a classical nonlinear adaptive control in a measurementand-feedforward process,while the nonclassicality is obtained by the cubic state.

Non-Gaussian ancilla is important to complete the cubic phase gate. It has been shown that the weak cubic nonlinearity can be prepared within reach of current technologies.[70]The nonclassicality of the approximative weak cubic state lies in the superposition of|1〉and|3〉. So, it can be heralded prepared as a superposition of Fock states. In detail, the idler mode from an entangled two-mode squeezed state is split into three by a pair of beam splitters, after which the states of the three modes are displaced in phase space.Simultaneous detection of a photon by the three detectors then heralds approximative preparation of the superposition state in the signal mode.

3. CV quantum simulation

Quantum simulation enables one to mimic the evolution of other quantum systems using a controllable quantum system.[71–74]A CV quantum computer may be more suitable for simulating CV quantum systems.[75]A scheme for simulating the Kitaev lattice model and detecting statistics of Abelian anyons is proposed,where a quadratic phase gate is used to detect the important feature of anyons,that is the nontrivial statistical phase obtainable through braiding.[76]In 2015,a quantum simulation scheme of quantum field theory using continuous variables was proposed.[77]Huhet al.proposed a quantum simulation scheme with modification of boson sampling, in which squeezed states of light are coupled to a boson sampling optical network to simulate the molecular vibronic spectra.[78]In 2018, Arrazola and Bromley showed that Gaussian boson sampling is a useful tool for dense subgraph identification.[79]In the same year,Br´adleret al. proposed a method to estimate the number of perfect matchings of undirected graphs based on the relation between Gaussian boson sampling and graph theory.[80]Very recently,Gaussian boson sampling was experimentally demonstrated using 50 single-mode squeezed states as the input states,[19]which shows the advantage of QC.In the experiment,50 indistinguishable single-mode squeezed states are sent into a 100-mode ultralow-loss interferometer with full connectivity and random matrix. The output states are sampled using 100 high-efficiency single-photon detectors, and the average fidelities around 0.99 are achieved in the experiment.

The experimental demonstration of CV quantum simulation is in progress. For example, quantum simulation for time evolution of quantum harmonic oscillators has been experimentally demonstrated by Denget al.[81]According to the Hamiltonian of a quantum harmonic oscillator=ω(†+1/2) in an open system with vacuum environment, the time evolution of the dimensionless position and momentum operators is given by

whereKis the decay rate, andx(t) andp(t) are the noise operators depending on the reservoir variables.

然而，地方财力不足的现状不能必然地导出消费税收入分配机制改革的合理性。税制变革应剖析其背后的理论依据。对此还有必要结合消费税改革进程，探究消费税收入分配机制调整的合理性，检视消费税收入分配机制调整与消费税其他改革措施的关联，以期能为理论研讨与立法调整有所裨益。

In the experiment, the Wigner function of the output state in phase space at different time points is measured to show the time evolution of a quantum harmonic oscillator in an open system for an initial coherent state and an initial amplitude-squeezed state,respectively. The measured fidelity,which is used for quantifying the quality of the simulation,is higher than its classical limit. This scheme may be used to simulate more complicated dynamical processes of quantum systems,whose Hamiltonian is described by the position and momentum operators. Generally, the Hamiltonian of the simulated system can be decomposed into a set of unitary transformations,[82]so its dynamic behavior will possibly be simulated by a sequence of quantum logic operations in CV QC and the coupling of qu-modes. For example, the simulation of interaction between two bosonic oscillators with strong coupling[83]could be implemented by CV quantum simulation.

4. CV quantum error correction

QEC is a necessary procedure to protect quantum information against errors in QC.[3]In the framework of CV error correcting codes, one class generalizes qubit stabilizer codes which is referred as linear oscillator codes to a CV system.[84,85]This class falls in the Gaussian quantum information. The other class encodes a discrete system into a CV system and this class of codes requires using non-Gaussian states. A scalable fault-tolerant architecture can be obtained by concatenating these two classes of codes.[86]

In the regime of CV QEC,according to the no-go theorem for Gaussian QEC that Gaussian errors cannot be corrected by using only Gaussian resources.[87]However,non-Gaussian stochastic errors, which frequently occur in free-space channels with atmospheric fluctuations for example,[88,89]can be corrected by Gaussian schemes. Different types of CV QEC codes for correcting single non-Gaussian error have been proposed, such as nine-wave-packet code,[85,90]fivewave-packet code,[84,91]entanglement-assisted code,[92]and erasure-correcting code.[93]Some CV QEC schemes against displacement errors have been experimentally demonstrated,for example, the nine-wave-packet code,[94]the five-wavepacket code,[95]and the correcting code with the correlated noisy channels.[96]It has been shown that in fault-tolerant CV QC with cluster state, initial squeezing in the cluster above a threshold value of 20.5 dB ensures that errors from finite squeezing acting on encoded qubits are below the faulttolerance threshold of known qubit-based error-correcting codes.[44]

The general process of QEC for QC and quantum communication is shown in Figs. 5(a) and 5(b), respectively. As shown in Fig. 5(a), in the QEC with stabilizer codes,[97]the encoded logical state|ψ〉Lis subject to an error process. Next,the code stabilizers are measured and the results are copied to a register of ancilla states|A〉⊗m. The ancilla states are then read out to give the syndrome resultS. In the decoding process,the syndrome result is used to determine the best recover operation to correct the errors. As shown in Fig. 5(b), in the QEC for quantum communication, an input state|ψ〉inand a set of ancillary states are encoded into a QEC code by the encoding circuit. The QEC code is transmitted through quantum channels where errors are introduced due to the noise in the environment. After the decoding circuit,the decoded ancillary states are used to identify the type and position of the error.By implementing a suitable error correction procedure based on the information in the syndrome procedure, the error will be corrected.

Fig.5. The general process of QEC.(a)The QEC for errors in QC with stailizer codes. (b)The QEC for errors in quantum communication.

4.1. CV QEC with five-wave-packet code

Here, we take the example of CV QEC with five-wavepacket code to show the concrete QEC procedure in quantum communication.[95]This five-wave-packet belongs to the QEC code [n,k,d]=[5,1,3], wheren=5 denotes the number of used wave packets,k=1 is the number of logical encoded input state, andd= 3 is the distance, which indicates how many errors can be tolerated,a code of distancedcan correct up to (d −1)/2 arbitrary errors at unspecified channels. The schematic of the QEC with five-wave-packet code is shown in Fig. 6, which contains five steps. (1) Encoding. The input state is coupled with four auxiliary squeezed states using a beam-splitter network consisting of four beam-splitters. The encoded five modes is a five-mode CV linear cluster entangled state as shown in Fig.6(a). (2)Error channel. The noise is randomly coupled into any one of the encoded five wave packets. (3)Decoding. The decoding circuit is the inverse of the encoding circuit, which also contains four beam-splitters.(4) Syndrome recognition. Measuring the decoded auxiliary modes by homodyne detectors. The error in different channels results in different outputs of the homodyne detectors,which is used to identify the position of the error. (5)Error correction.Feedingfoward the corresponding measurement results of homodyne detectors to the output mode by the EOMs according to the error syndrome results.

After the error correction, single displacement error in phase space caused by channel noise is corrected. In this CV QEC experiment,the information of the input state is only distributed on three of the five channels and thus any error appearing in the remained two channels never affects the output state, i.e., the output quantum state is immune from the error in the two channels. The stochastic error on a single channel is corrected for both vacuum and squeezed input states and the achieved fidelities of the output states are beyond the corresponding classical limit.

Topological code is a special stabilizer QEC code whose generators are local but logical operators are topologically nontrivial and nonlocal.[98]Errors can be detected by measuring stabilizer operators.CV topological codes require new features such as the direction of edges,signs for anyonic charges,and more complicated string operators, such as fusion rules,and braiding rules.[98]In addition,some other concepts related to it have been proposed in recent years,such as the CV anyon statistics,[76]the graphical calculus for CV states[99]and its application in quantum communication,[100]the CV QC with anyons,[101]the exploration of CV fault-tolerant QC,[102]and topological entanglement entropy.[103]

Fig. 6. The schematic of CV QEC with five-wave-packet code. (a) The graph representation of the five-wave-packet code. The input state is encoded on submodes 3, 4, and 5 of a five-partite linear cluster state 1−5. (b) The schematic of experimental set-up. EOM: electro-optical modulator, T1−4:beam-splitters with 25%,33%,50%,and 50%transmission,respectively. D1−4: homodyne detectors. Revised from Fig.1 in Ref.[95].

4.2. CV QEC with correlated noisy channel

In 2016, Denget al. experimentally demonstrated the disappearance and revival of the squeezing in quantum communication with squeezed state by using a correlated noisy channel.[107]In 2017, the disentanglement and the entanglement revival of a tripartite entangled state were also experimentally demonstrated.[108]Disentanglement is observed when the excess noise exists in the quantum channel. By creating a correlated noisy channel, entanglement of the tripartite entangled state is preserved, thus disentanglement can be avoided with the correlated noisy channel.

4.3. Fault-tolerant architecture

It has been shown that fault-tolerant linear optical quantum computing can be realized using two coherent states as a qubit basis.[102]Noiseless linear amplification (NLA) is the key operation to correct the error introduced by Gaussian noise.[109]In 2011, Ralph proposed a CV QEC protocol that can correct the Gaussian noise induced by linear loss on Gaussian states.[110]This protocol is based on CV quantum teleportation and heralded NLA,which can be implemented by using linear optics and photon counting. A probabilistic NLA was experimentally demonstrated to amplify coherent states at the highest levels of effective gain based on a sequence of photon addition and subtraction.[111]It has also been shown that measurement-based NLA, which is equivalent to the heralding NLA,can be implemented by performing a post-selective filtering on the measurement results.[112]

The non-Gaussian operations are critical to fault tolerance of CV QC. The hybrid approach that takes advantage of both deterministic CV operations and robust qubit encoding becomes a trend in CV QEC.[66,86]Many different encoding schemes for CV QEC have been proposed such as GKP code,[66]encoding in cat states[102]and binomial states.[113,114]For these codes,a qubit is encoded on a square lattice in phase-space in a way that allows for the suppression of relevant errors (such as loss) to a certain extend.[115]Concatenating the GKP code with other qubit error correction code,for example toric GKP code,[86]surface-GKP code,[116]and the non-Gaussian oscillator-into-oscillators code,[117]provides a feasible method to correct general errors. It has been shown that initial squeezing in the cluster state above a threshold value of 20.5 dB ensures that errors from finite squeezing acting on encoded qubits are below the fault-tolerance threshold of known qubit-based error-correcting codes, which is a necessary condition for fault-tolerant measurement-based CV QC.[44]

5. Discussion and conclusion

Tremendous progress has been made in CV QC and QEC in recent years, as we reviewed in this manuscript. However,there are still some challenges for realization of universal and practical CV QC. Firstly, the cubic phase gate, which is a necessary quantum gate for universal CV QC, still remains a challenge although several proposals have been presented.Secondly, fault-tolerant CV QC is another challenge which is worth of further study. Thirdly, toward practical QC, it is essential to develop integrated quantum chips that include quantum source, circuits, and detectors for CV system. For example, CV chips for entangled state[118,119]and squeezed state[120–123]have been demonstrated, which demonstrate the feasibility of integrated quantum chips for CV system.

In summary, we briefly reviewed the progress of measurement-based CV QC and QEC,including the theoretical proposals and experimental demonstrations. We also discussed the fault-tolerant structure of CV QC and challenges ahead for realization of universal and practical CV QC.As the large scale CV cluster state in time domain has been achieved,it provides sufficient quantum resource for CV QC.Since non-Gaussian operation is required for universal measurementbased CV QC, it is essential to develop hybrid quantum information processing system that combines both DV and CV systems.[124]