基于局部敏感哈希-双层随机森林的燃气轮机剩余使用寿命预测

白玉金， 康英伟， 黄 伟， 茅大钧， 鲍克勤

(上海电力大学自动化工程学院， 上海 200090)

燃气轮机是一种重要的动力机械，是一个涉及国家能源和国防安全的战略性产业，被誉为“制造业皇冠上的明珠”，应用范围越来越广，越来越受到人们的关注[1-2]。燃气轮机在航海、航天和电力方面发挥着重要的作用，特别是近几年随着国家大力提倡环保发电，燃气-蒸汽联合循环发电不仅满足环保要求，而且能够达到比较高效的发电，燃气轮机在电厂中的地位不断提高。

然而，由于燃气轮机长期工作在高温高压的恶劣环境下[3]，导致燃烧室、喷嘴、燃气透平静叶等一些部件时常发生故障，随着运行时间的增加,燃气轮机的关键部件难免会达到寿命极限，此时就不得不进行维修维护。若能及时根据燃气轮机的剩余使用寿命安排合适的维修维护，就能大大减少事故和停机，提高效率。因此研究燃气轮机的剩余使用寿命(remaining useful life，RUL)预测具有重要的意义。

对RUL的预测方法有物理模型法和数据驱动预测法。物理模型的预测方法，通过利用燃气轮机的工作原理等，对其进行建模，并把模型结合到退化估计中，实现对RUL的预测。然而在大多数情况下，复杂系统的数学模型的建立是困难的，以传感器获得的数据为起点的数据驱动的方法就显示出其优越性。黄亮等[4]把排气温度裕度作为燃气轮机的剩余使用寿命的退化指标，建立多阶段非线性Wiener过程性能退化模型，实现了燃气轮机的RUL预测。Zaidan等[5]把变分推理应用到贝叶斯分层模型，实现用排气温度裕度表示的燃气轮机的RUL概率估计；Wang等[6]基于多环境相似理论，把运行时间和启动次数作为退化指标进行RUL预测，并实现预后决策；Tsoutsanis等[7]通过局部拟合预测发动机性能行为的线性回归模型，准确地预测压缩机在动态操作模式下的退化情况。

然而，目前对单一监测变量的退化表示燃气轮机故障退化建模分析的研究比较多，以及表示燃气轮机的退化模式常常比较简单。针对燃气轮机剩余使用寿命预测中监测数据信息利用不够充分、退化过程难以表示、预测精度低等问题，现拟对多维监测变量进行信息融合，构建燃气轮机性能退化曲线并用基于相似度的方法查询与需要预测的退化曲线最相似的历史退化曲线，进一步采用双层随机森林模型进行RUL预测，在C-MAPSS数据集[8]上对提出的方法进行验证。

1 局部敏感哈希-双层随机森林剩余使用寿命预测方法

1.1 基于局部敏感哈希-双层随机森林的燃气轮机RUL预测框架

基于局部敏感哈希(local sensitive Hash,LSH)-双层随机森林的燃气轮机RUL预测流程图如图1所示，主要包括以下三个部分。

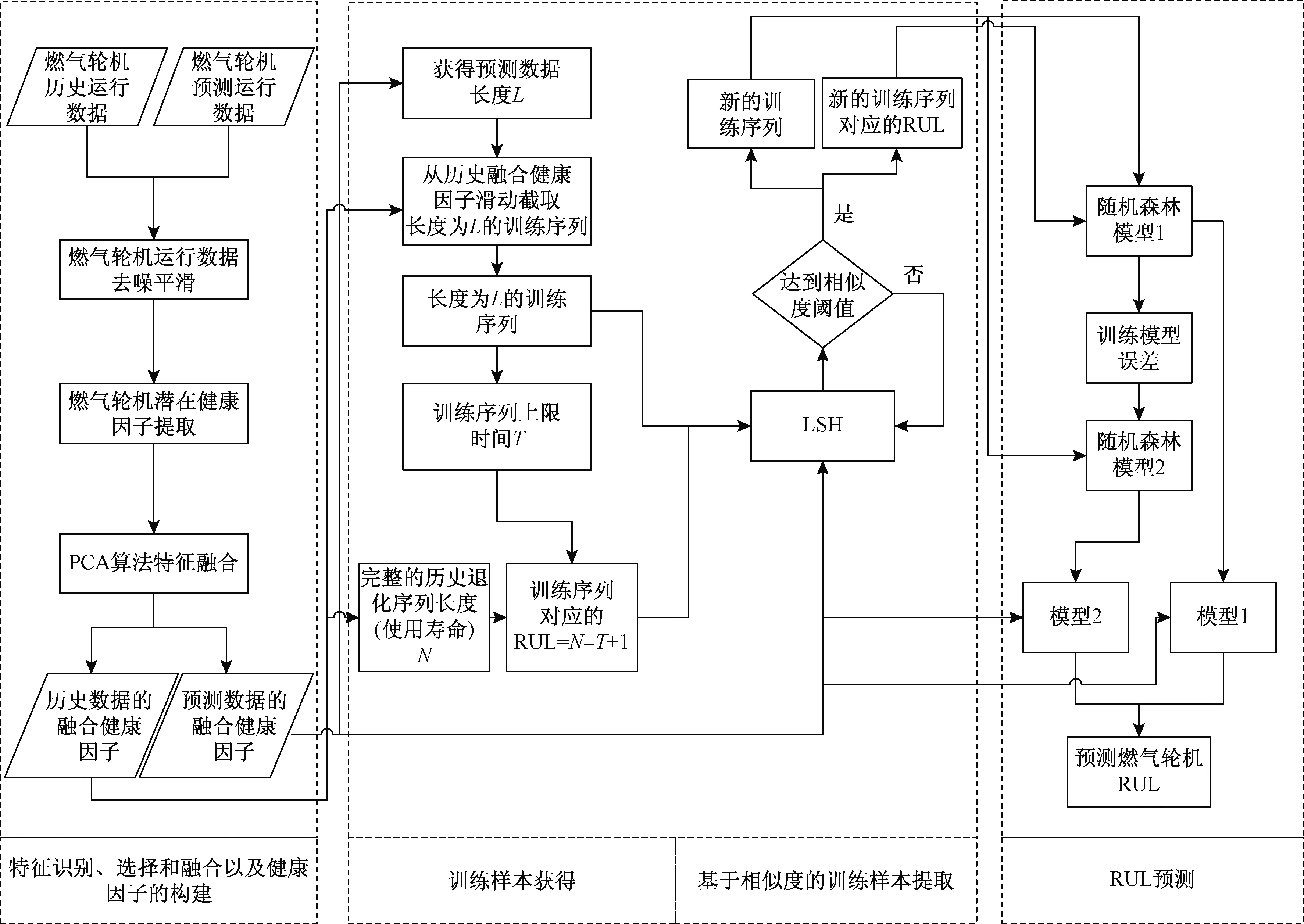
图1 基于LSH-双层随机森林的燃气轮机RUL预测流程图Fig.1 Flow chart of gas turbine RUL prediction based on LSH-double-layer random forest

(1)燃气轮机特征识别、选择和融合以及健康因子(health index, HI)的构建。包含多维燃气轮机传感器数据的选择，对选择的特征数据进行去噪、平滑，并用主成分分析法算法对有相关性冗余的特征进行去噪、降维，从而构造健康因子。

(2)训练样本获得。从获得全寿命的历史退化曲线中，通过从左向右滑动的方式截取与需要预测的数据同长度的训练数据。全寿命的历史退化序列的长度减去训练数据的上限加一即为训练数据相对应的RUL。

(3)基于相似性的训练数据提取。以训练序列和预测训练的欧式距离为度量，通过p-stable 分布局部敏感哈希(local sensitive hash, LSH)相似性搜索算法，获得基于相似度的训练数据。

(4)构建燃气轮机RUL预测模。利用基于相似度的训练数据，通过双层随机森林的做回归训练得到预测模型，将预测数据输入到模型实现燃气轮机剩余使用寿命的预测。

1.2 基于主成分分析算法的健康因子构建

虽然现在燃气轮机的性能显著改善，但是燃气轮机的结构复杂和工作条件的恶劣，长期工作不可避免会出现各种故障。此外，在燃气轮机的启停和可变条件操作期间，复杂的热-机械负荷通常会对许多关键部件的可靠性造成威胁，并降低燃气轮机的剩余使用寿命。考虑到尘埃颗粒、烟雾和高湿度等环境因素，包括压缩机在内的气路组件的性能会随着燃气轮机使用寿命的增加而不同程度地退化[9]。虽然燃气轮机内部退化结构复杂，但其性能退化规律可通过燃气轮机外部测量参数或者某些物理量的变化规律反映。

燃气轮机外部测量量有：高压压气机出口温度、风扇进口压力以及高压涡轮排气量等。外部测量量众多、数据维度高，而且数据之间还存在着一定的相关性，因此使用主成分分析方法(principal component analysis，PCA)对数据需要进行选择和融合。

PCA算法是一种常用的数据降维、数据融合和降噪的方法。使用PCA对数据进行处理，得到降噪、降维后的数据主成分。然后根据得到的主成分，利用T2统计量构建健康因子。PCA及基于PCA模型的统计量T2的健康因子构建的主要过程如下。

(1)数据标准化。假设燃气轮机样本观测数据矩阵为X，表达式为

(1)

式(1)中：n为单个燃气轮机运行数据样本的总数；p为燃气轮机的总特征指标数；xij燃气轮机第i个运行数据样本的第j个特征指标。

按照式(2)对原始数据进行标准化处理，即

(2)

(2)计算数据相关系数矩阵R，即

(3)

式(3)中：相关系数矩阵R中第i′行第j′列的数据ri′j′为标准化后的样本观测数据矩阵X*的第i′列元素xi′和第j′列元素xj′的协方差。

(3)求相关系数矩阵R的特征值λ1≥λ2≥…≥λp及特征值对应的特征向量μ1，μ2，…，μp。

(4)分别根据式(4)、式(5)计算每个特征根的贡献率Ci和累计贡献率C，即

(4)

(5)

(5)确定主成分及健康因子构建。C的取值依据通常是达到85%以上，得到所选主成分的个数k。根据式(6)计算主成分，并根据式(7)、式(8)计算T2统计量，从而构建健康因子。

(6)

(7)

(8)

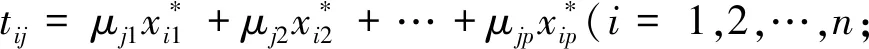
1.3 训练样本的获取与基于p-stable 分布LSH相似性搜索算法的数据再获取

1.3.1 训练样本的获取

如图2所示为三个由健康因子表示的燃气轮机的性能衰退曲线，其中一个为全寿命的性能退化曲线，包括燃气轮机从正常工作到因故障停止工作的全过程，代表全寿命历史退化序列；另外两个不完整的燃气轮机健康因子曲线表示预测数据序列，只包括从开始运行到当前运行时间的性能退化过程。每条曲线由均有若干点组成，每个点代表该燃气轮机的性能退化状态，可由基于PCA获得的健康因子Ti2表示。

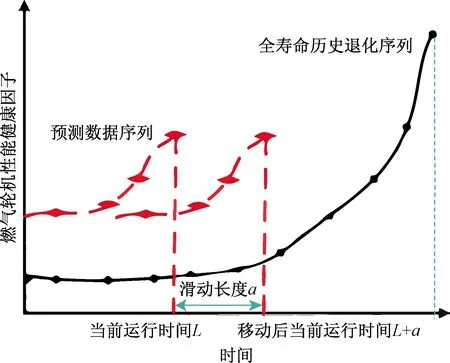
图2 寿命预测训练数据的获取Fig.2 Acquisition of training data for life prediction

不同燃气轮机的性能退化序列的长度各不相同，如第i个为燃气轮机性能退化序列的长度为Ni，性能衰退序列为Ti，预测燃气轮机数据序列长度为L，性能退化序列Y。而在燃气轮机剩余寿命预测模型中，为了比较不同的燃气轮机的性能退化相似度，即比较健康因子曲线的相似度，一般要求两个健康因子曲线的长度相等。首先在历史燃气轮机的全历史性能退化序列Ti中，截取L长度的子序列，然后与需要预测燃气轮机的性能退化序列Y对比并计算距离。

由于燃气轮机以用户未知的不同程度的初始磨损和制造变化开始，而且为了增加训练样本的数量，提高预测的精度，通过从左向右依次滑动一个时间间隔的方法获得多组训练数据。如图2所示，刚开始从全寿命历史退化序列的原点位置截取同预测数据同长度的序列作为训练序列Xtrain1，即对应于图2中全寿命历史退化序列中的0～L序列，其对应的RUL可以由式(9)求得。向右滑动a个单位时间间隔，此时的训练序列Xtrain，a+1对应于图2中全寿命历史退化序列中的a～a+L序列，其对应的RUL可以由式(10)求得。

通过上述方法便可以在不同的燃气轮机全寿命退化序列上获得足够多的训练数据集Xtrain={Xtrain1Xtrain2,…,Xtrain,n}，及其对应RUL训练数据集RULtrain={RULtrain1RULtrain2,…,RULtrain,n}。

RULtrain1=N-L+1

(9)

RULtrain ,a+1=N-(L+a)+1

(10)

式中:a=1,2，…，N-L。

1.3.2 基于p-stable 分布LSH相似性搜索算法的数据再获取

通过滑动截取全寿命历史退化序列可以得到大量的训练数据，如何在大量的数据中找到与预测数据最相似的训练数据关乎预测结果的精度问题。局部敏感哈希是一种针对海量高维数据的快速最近邻查找算法[10]，能实现在大量的训练数据中查找与预测数据最相似的数据，实现数据的降维和近邻查找。

LSH基本思想是：高维空间的两点若距离很近，那么设计一种哈希函数对这两点进行哈希值计算，使得他们哈希值有很大的概率是一样的。同时若两点之间的距离较远，他们哈希值相同的概率会很小。局部敏感哈希是由满足一定条件的函数簇组成。针对不同的相似度测量方法，局部敏感哈希的算法设计也不同。以Lp范数下的欧氏距离来度量数据相似度，因此需要基于p稳态分布来构造哈希函数。

基于p稳态分布LSH相似性搜索算法的数据再获取可分为以下几步[11]。

(1)p稳态分布LSH函数族的构造。文献[12]提出了基于p稳定分布的函数族，其中每个哈希函数定义为

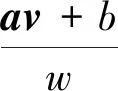
(11)

式(11)中:a是一个由随机取自p稳定分布的数组成的d维向量；p稳定分布的LSH函数把向量v投影到向量a上，然后w被当作量化间隔进行对投影的量化；b为投影偏差的一个修正量，b∈[0,ω]，是一个随机实数。

(2)从构造的LSH函数族中，随机选取L组哈希函数，每组由k个哈希函数构成，记为

g={g1(·),g2(·),…,gL(·)}

(12)

式(12)中：gi(·)=[h1(·),h2(·),…,hk(·)]。

(3)产生两个哈希函数H1和H2。如果把一个函数组对向量的一组哈希值(x1,x2,…,xk)=[h1(vi),h2(vi),…,hk(vi)]直接放入哈希表，即使用了大量的内存，又不便于对哈希值的查找，因此需要另外定义两个哈希函数。

H1的值作为哈希表索引，H2的值作为链表中的关键值,具体形式为

(13)

(14)

式中:ri和r′i是两个随机整数。

(4)将每一个高维特征向量Xtrain,i，用哈希函数gi进行哈希得到(x1,x2,…,xk)=[h1(Xtrain,i),h2(Xtrain,i),…,hk(Xtrain,i)]。

(5)将(x1,x2,…,xk)用H1进行哈希得到index，而value是由(x1,x2,…,xk)用H2进行哈希得到的。

(6)高维特征向量被插入由index确定的桶，并记录其value值。直到L个桶中存在每个高维特征向量(x1,x2,…,xk)哈希为止。

(7)对于需要查询的特征向量Xforecast同样执行步骤(5)(6)得到其value值记为Valueforecast。

(8)查询Valueforecast是否在高维特征向量(x1,x2,…,xk)哈希到的L个桶内,若在则返回(x1,x2,…,xk)用H1进行哈希得到index。

(9)由得到的index在Xtrain={Xtrain1，Xtrain2,…,Xtrain,n}得到新的训练样本集X′train={X′train1,X′train2,…,X′train,n}，计算新的训练样本集X′train和Xforecast之间的欧氏距离，并对距离排序，从而获得K个近邻点。若满足设定K值则得到新的训练样本集X′train，及其对应的RUL训练集RUL′train，否则调整参数L、k重新执行(1)～(8)步直到满足要求。

1.4 双层随机森林

随机森林是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于集成学习方法[13]。由于随机森林模型只有两个参数树的数目n与每个节点处的特征数目p需要设置，而且模型对于两个参数的取值不敏感，所以一般不会过拟合。为了提高模型的精度，本文采用双层随机森林对数据进行回归预测RUL。

双层随机森林[14]包括两层，每一层都有一个智能学习模型，两个模型串联执行。第一层和传统的回归方法一样，并添加第二层对第一层随机森林模型回归训练的误差进行建模，以减少建模误差对模型的影响。

双层随机模型如图3所示，模型对燃气轮机的RUL进行预测可分为两个阶段：模型训练阶段和模型回归预测阶段。在模型训练阶段，将上一步基于p稳态分布得到的新的训练集X′train及其对应的RUL训练集RUL′train作为随机森林模型1的输入，进而得到模型的预估计值，并把它与模型的输入RUL′train做比较得到模型的预估计残差。接下来，随机森林模型2对预估计残差进行建模。模型2的输入为模型1的预估计误差和基于p稳态分布得到的新的训练集X′train，进而得到模型1的预估计残差的估计误差。因此，当将模型2输入到模型1中时，模型2可以表示训练集输入与估计误差之间的关系，即模型2通过对模型1的错误进行建模来提高模型1的准确性。在模型训练之后，便可以用于模型对新的序列进行回归预测。将需要预测的序列X′forecast同时输入到训练好的模型1和模型2，模型1可以产生估计量RUL′forecast，而估计误差RUL″forecast可以从模型2获得。然后，可以通过将需要预测的序列的预估值和预估误差相加来获得燃气轮机剩余寿命预估值RULforecast，即通过式(15)计算燃气轮机剩余寿命，即

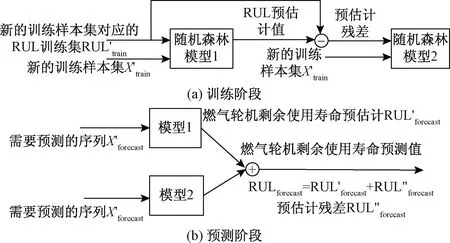
图3 双层随机森林模型Fig.3 Two-layer random forest model

RULforecast=RUL′forecast+RUL″forecast

(15)

2 应用结果与分析

2.1 实验数据

实验数据是C-MAPSS数据集中第1组数据(FD001)，FD001是由训练数据集、测试数据集和测试数据的剩余使用寿命数据集组成，该数据集记录的是单工况模式下的燃气轮机运行数据。训练集和测试集均包含100台测试燃气轮机的运行序列，训练集中的序列包含从初始正常状态到故障刚刚出现，故障会不断增加，直到系统出现故障完全停止工作为止，即燃气轮机的全寿命序列。而在测试集中，时间序列在系统故障之前的某个时间结束。每个燃气轮机的初始磨损和制造变化是不同的。这种磨损和变化被认为是正常的，也就是说，它不被视为故障状况。

燃气轮机所监测的参数有：高压压气机出口温度、低压涡轮出口温度、风扇进口压力等21个参数，每个参数的数据都被噪声所污染。

2.2 特征提取与健康因子构建

虽然原始数据集中提供的有21个传感器监测的参数的序列数据，但是并不是所有特征都表现出一定的可以用来进行剩余使用寿命预测的趋势。如图4所示的几个特征，在整个运行周期内为恒定值，对剩余使用寿命预测的贡献微乎其微。只有那些在燃气轮机的整个寿命范围内表现出一定的趋势的特征，才能够表征燃气轮机的退化趋势，进而用来构建健康因子进行燃气轮机的剩余使用寿命预测。而且为了得到更高精度的预测寿命的还需要对特征进行进一步的提取，根据文献[15]中选择的七个传感器2、3、4、7、11、12和15号作为提取的特征进行健康因子的构建，具体各传感器获得的数据如图5所示。

图4 燃气轮机特征参数Fig.4 Gas turbine characteristic parameters

由图5可知，随着燃气轮机性能逐渐退化，数据都呈现单一趋势，要么增加，要么减少。有大量噪声存在于监测数据中，需要对监测数据进行滤波操作。使用MATLAB中的高斯滤波器对监测数据进行滤波操作，窗口宽度设置为10，滤波后的数据如图6所示。滤波后，在微小数据变化范围内，数据平滑度增加，趋势逐渐稳定，大量噪声被滤去。

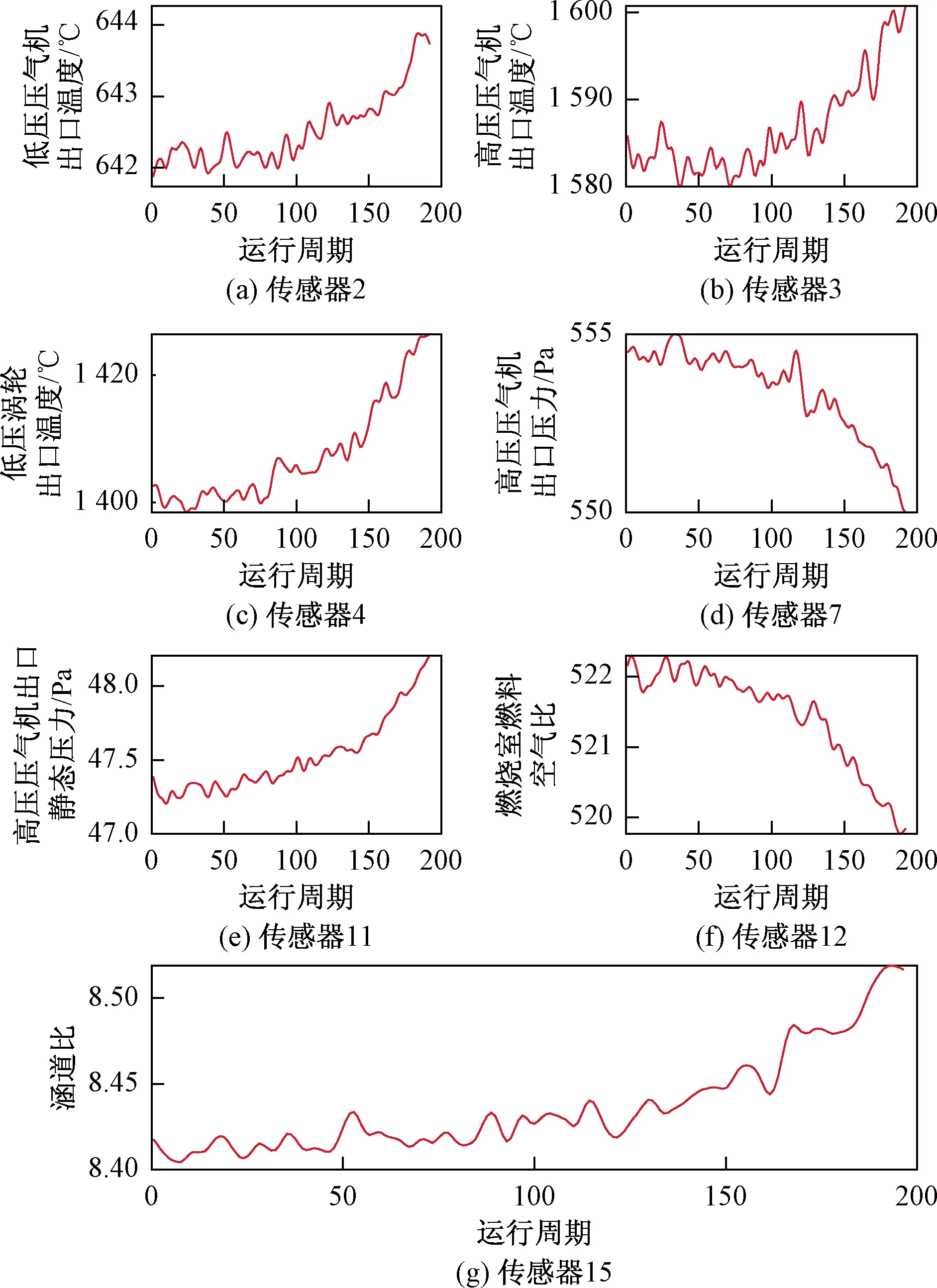
图6 2、3、4、7、11、12和15号传感器滤波后数据Fig.6 Filtered data of sensors 2, 3, 4, 7, 11, 12 and 15

为了进一步滤波和消除每个传感器得到的数据之间数量级之间的差异，对滤波后的数据利用PCA模型进行归一化操作，并根据利用PCA模型的统计量T2来构建燃气轮机的健康因子。基于T2统计训练集燃气轮机健康指标如图7所示，由图7可得，随着燃气轮机运行周期的增长，基于PCA获得的健康因子曲线前期的退化速率较小，趋于平滑，而后期的退化速率则以近似指数曲线形式变化。这和燃气轮机退化初期不明显，后期快速变化的特点相吻合。

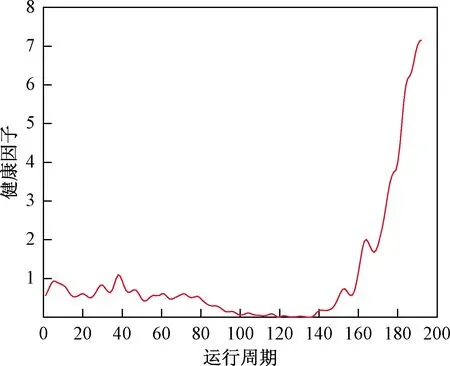
图7 1号燃气轮机的健康因子Fig.7 Health factor of No. 1 gas turbine

2.3 相似数据获取

采用滑动的方法在上述获得燃气轮机健康因子曲线上，依次截取与预测数据等长度的序列作为训练序列。如图8所示为在1号燃气轮机全寿命历史退化序列中，通过滑动的方式获得需要预测的1号燃气轮机的训练样本的过程。图中燃气轮机全寿命历史退化序列包含192个单位运行周期，即N=192。需要预测的燃气轮机包含31个单位运行周期，即L=31。观察两个时间序列可知，初期的变化趋势不完全一直，但是变化不大，都属于正常的运行周期。通过向右滑动的方式，获得与预测序列的同长度的大量训练序列集。

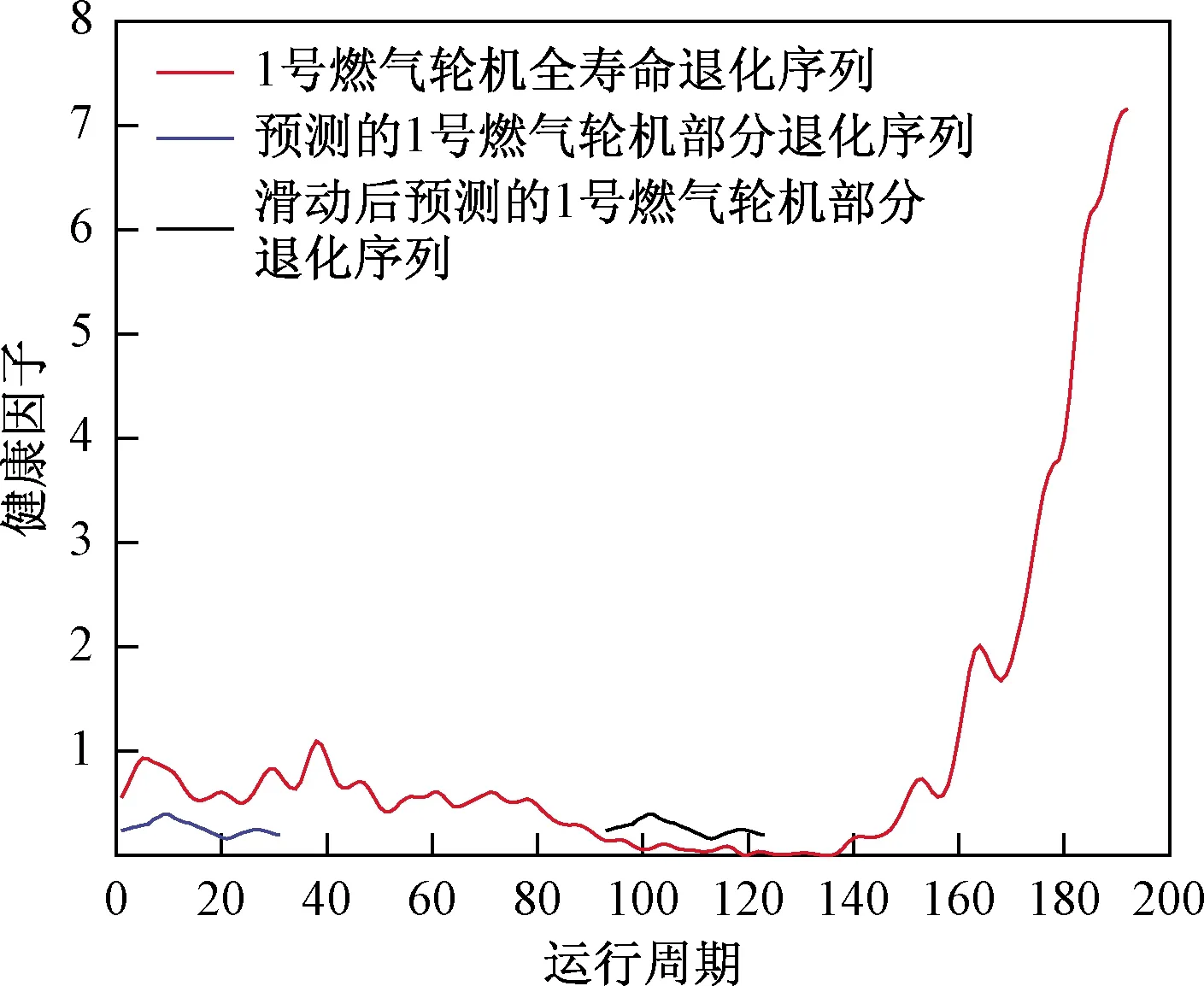
图8 使用固定窗口长度滑动方法获得训练数据Fig.8 Using a fixed window length sliding method to obtain training data

通过滑动方式获得了大量数据，例如1号燃气轮机预测数据集中有17 631个训练数据。通过基于p稳态分布LSH相似性搜索算法，找出训练序列集与预测序列最相似的数据组成新的训练集作为双层随机森林模型的输入,参数设置为：ω=1、哈希表的大小tableSize=20，近邻点数量K设为100，并调节参数哈希函数组L、哈希函数个数k使满足阈值要求。

2.4 剩余使用寿命预测

为了提高预测的精度，采用双层随机进行剩余使用寿命预测。随机森林模型一般不会过拟合，并且只有两个参数需要设置，而且模型对于两个参数树的数目n与每个节点处的特征数目p的取值不敏感[16]。回归树的数目n=50，每个节点处选择的特征数目p=4。

根据文献[8]的定义，预测误差为

E=RULforecast-RULtrue

(16)

式(16)中：RULforecast为预测的剩余使用寿命(飞行循环次数)；RULtrue为实际的剩余使用寿命。根据此预测误差定义误差函数为

(17)

预测结果分为三种：准确预测、提前预测和滞后预测。当E>13为提前预测，E<-10为滞后预测，-10≤E≤13为准确预测。误差函数倾向于提前预测，因为其对于提前预测的惩罚力度小于滞后预测。这也与实际情况相吻合，提前预测只是降低了燃气轮机的使用率，但滞后预测可能带来一定的事故。

图9为利用上述方法预测的结果，可知预测结果接近于真实剩余使用寿命，表明了所提出方法的可行性。预测的误差分布如图10所示。预测误差分布在[-50,50]之间，且准确预测误差达到50%以上，滞后预测误差比例较小，进一步表明了所提出方法的可行性。

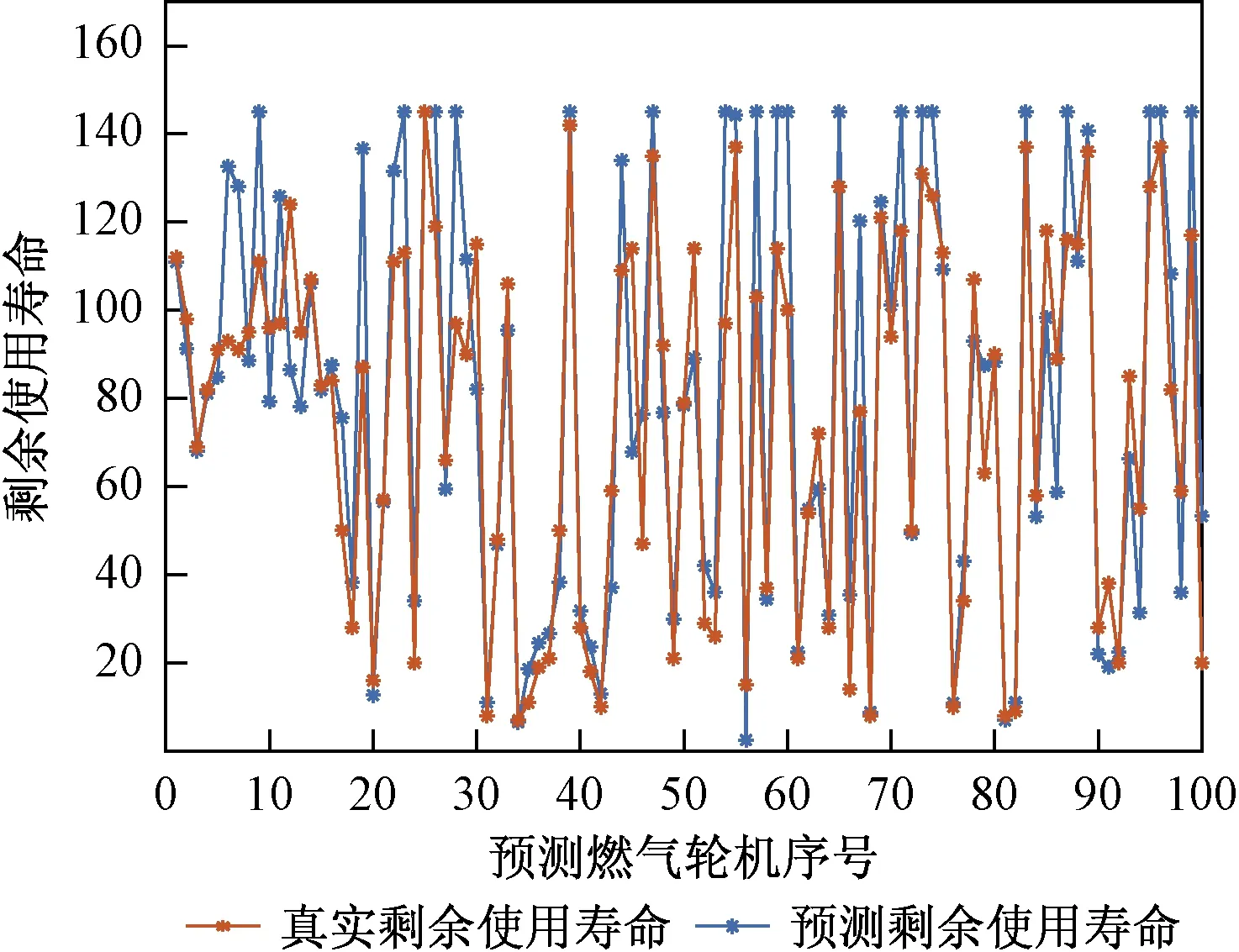
图9 燃气轮机剩余使用寿命预测结果Fig.9 Results of prediction of remaining useful life of gas turbine

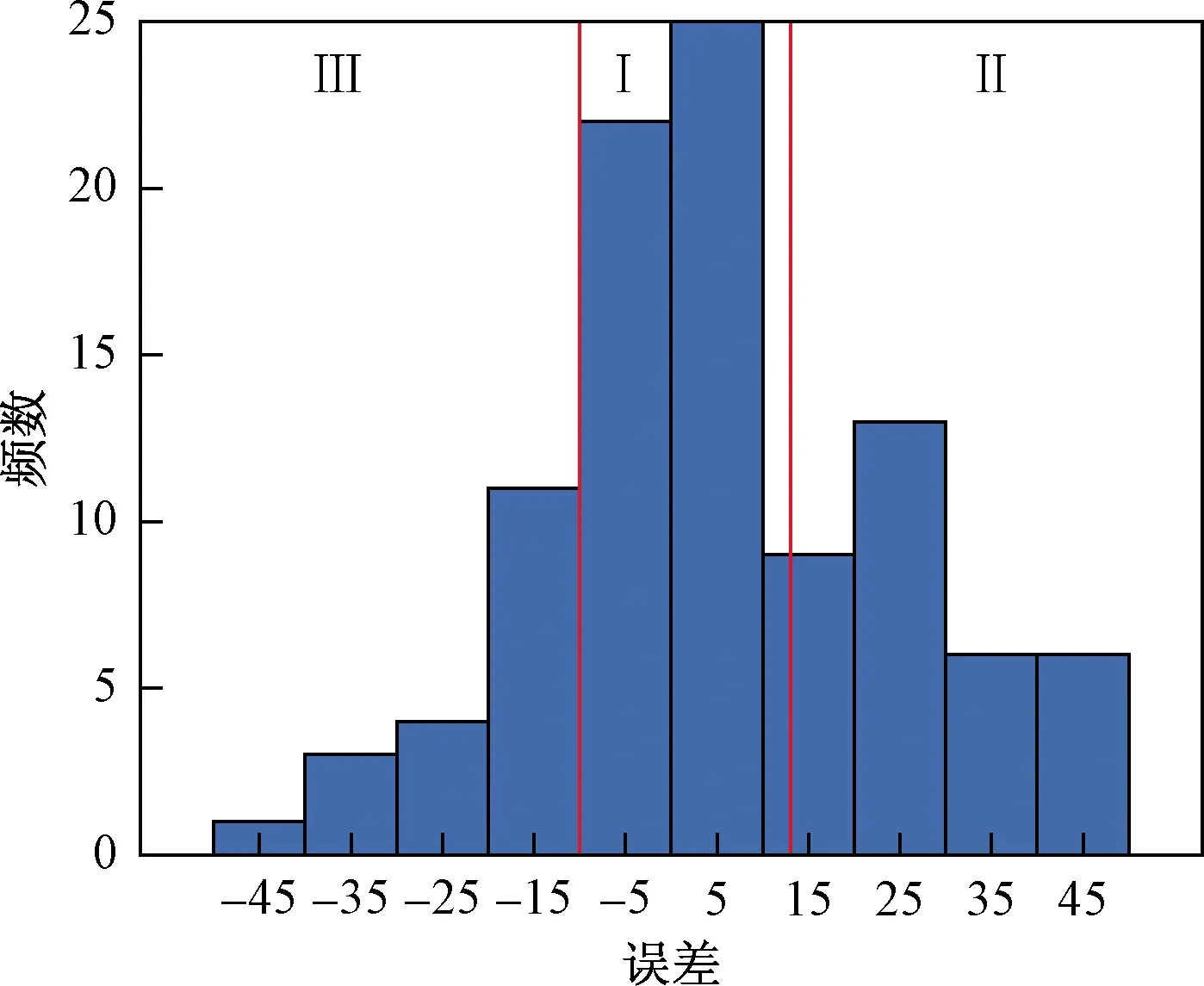
Ⅰ为准确预测；Ⅱ为提前预测；Ⅲ为滞后预测图10 预测误差分布Fig.10 Forecast error distribution

表1为两种不同预测方法的比较，可知双层随机森林预测的各种指标优于单层随机森林预测的各项指标。

表1 不同预测方法的比较Table 1 Comparison of different forecasting methods

3 结论

针对目前燃气轮机剩余使用寿命预测建模分析存在监测数据信息利用不够充分的问题，本文提出了基于主成分分析的燃气轮机多维数据融合方法，并使用PCA模型的统计量T2构建健康因子来表征燃气轮机的退化过程。为了提高剩余使用寿命预测的精度，在序列相似性的基础上提出了双层随机森林回归预测模型，结论如下。

(1)所提出的预测方法预测的结果接近于真实剩余使用寿命，并且预测误差在分布在[-50,50]之间，且准确预测误差达到50%以上。

(2)提出的双层随机森林模型在误差函数得分、准确预测单元个数等方面均优于单层随机森林。