基于最小二乘-分步解耦的泄渗漏带与隧道围岩渗流参数方法
张 鹏, 李彦霈, 田世宽, 万 飞, 王占强, 胡 波
(1.南京工业大学交通运输工程学院, 南京 210009; 2.中交一公局第四工程有限公司, 南宁 530000; 3.交通运输部公路科学研究所, 北京 100088)
涌水突泥是岩溶区隧道工程的主要地质灾害之一。岩溶岩体渗透能力主要取决于连接孔隙空间的通道大小[1-2]。由于岩溶发育具有随机不均匀性,溶腔孔隙及其连接通道的分布、规模和组合导致其呈现显著的随机性、不均匀性[3],从而致使工程中很难依据钻孔资料对岩溶隧道涌水量做出可靠估计。尽管已有研究表明,岩溶岩体涌水量主要受岩腔及其周边岩体的渗透系数控制[4]。然而,目前还没有一种准确、可靠地确定岩溶溶腔渗流性能的试验方法或解析方法[5]。
现场抽水试验和渗流参数反演是当前确定岩体渗透参数的常用方法。尽管现场抽水试验是确定渗透参数最为经典水文地质方法之一[6],但其以多孔介质的达西定律为基础,普遍存在数据离散和代表性不强以及费用高等问题,且其对于高度非均匀非均质的喀斯特岩溶的适用性尚未得到公认[7-9]。同其他岩土工程问题一样,采用基于实测数据进行岩体渗流参数反演是确定渗透参数较为理想的方法。纪成亮等[10]利用压水试验数据反演了裂隙岩体渗透参数;王媛等[11]通过动态观测总结水头、位移等多类型资料,建立渗流场与应力场在裂隙岩体中动态全耦合的参数反演思路;张振昌等[12]对胡麻岭隧道7号竖井进行了野外现场定流量抽水试验,以实测数据为依据,应用布尔顿配线法、直线法以及水位恢复法分别得到了第三系粉细砂岩渗透系数;唐连松等[13]为得到模型中两个关键层位的岩体渗透系数场,以PEST(parameter estimation)参数优化算法对地下水封洞库低渗岩体渗透系数进行反演,;Gan等[14]基于非稳定渗流试验成果提出了一种裂隙岩体渗流参数的综合反分析技术;Zhao等[15]基于矿井涌水事件反演了岩体的渗透系数;Liu等[16]基于达西定律反演分析了煤岩的气渗透系数;Zhang等[17]采用微震数据反演了页岩的渗透系数;Liu等[18]反演预测了热裂干岩的渗透率变化;Fang等[19]采用混合遗传算法反演了岩体的孔隙率、饱和度及渗透系数;Wang等[20]基于流动电流检测反演了岩体渗透系数。李永寿等[21]采用已有的损伤演化方程,通过渗透系数与损伤之间的定量关系,来刻画岩体扰动过程中渗透系数的变化规律。尽管上述研究中有部分成果还处于理论研究阶段,但亦有许多已应用于实际工程中,这表明采用反演分析确定岩溶岩体渗透系数是可行的。
围绕鸡冠山隧道涌水数据资料,首先釆用电法和地质雷达探测方法查明了隧道上覆岩溶溶腔的分布状态,从而结合工程地质勘察资料构建了上覆天坑降雨入渗的渗流地质模型,然后采用基于最小二乘-分步耦合优化方法的岩溶隧道围岩渗流参数反演法,以3个涌水事件的涌水量、涌水速率、涌水与降雨关联时间、天坑积水水头为反演边界条件,关联性解耦下泄渗漏带与隧道围岩渗流规律,最终通过分步优化探讨了下泄渗漏带和隧道围岩的渗透系数,以期为工程安全性评价提供参数取值依据。
1 工程概况与模型构建
1.1 鸡冠山隧道概况
鸡冠山隧道位于贵州省威宁县炉山镇境内,为典型岩溶地层条件下的特长分离式越岭隧道,左线隧道起讫里程桩号为ZK70+238~ZK74+010,长3 772 m,右线隧道起讫里程桩号为YK70+235~YK74+035,长3 800 m,隧道总体呈S形展布,洞身主体呈北东-南西向展布,洞身走向方位角为248°,进出口段均略呈弧形展布,其中进口段路线走向约274°,出口段走向约265°。隧道建筑限界为10.25 m×5 m(宽×高),设计纵坡1.4%,时速度80 km/h,采用灯光照明,机械通风。
鸡冠山隧道区域构造属溶蚀峰丛洼地地貌,峰丛基座相连,溶丘与洼地相间展布,漏斗、落水洞等地貌发育,如图1所示。穿越区溶蚀丘峰峰顶多呈长椭圆-浑圆状,山脊狭长,脊顶地形较缓,受本区构造控制,多呈近东西向展布。鸡冠山隧道穿越段自然地面标高2 040~2 244 m。岩溶天坑中心桩号为K72+280,沿隧道方向范围为K72+220~K72+340,距离隧道洞顶76 m,地层走向和隧道轴线之间大角度斜交。隧道区出露基岩为二叠系下统茅口组(P1m)灰岩、二叠系下统栖霞组(P1q)灰岩、二叠系下统梁山组(P1l)泥岩、石炭系上统马平组(C3mp)灰岩,石炭系中统黄龙组(C2hl)灰岩。其中,进洞口地层为茅口组(P1m)灰岩,岩层产状为15°~35°∠21°~27°,出洞口地层为石炭系中统黄龙群(C2hl),岩层产状为73°~80°∠32°~49°。区内陡倾构造及溶蚀节理裂隙发育,节理主要以走向NE35°~45°、倾向北西和南东、倾角65°~85°和走向NW30°~65°、倾向北东和南西、倾角60°~80°的张裂隙为主,裂隙线密度可达2~4条/m,延长2 m、切深3~5 m,裂面起伏,透水性好,是地表水下渗的重要通道。

图1 天坑、落水洞Fig.1 Karst pit and catavothre
鸡冠山隧道位于亚热带季风湿润气候区,雨量充沛,气候宜人。据威宁气象站资料,多年平均降水量为960.6 mm,蒸发量1 407 mm,日最大降水量为166 mm,极端最高气温35.7 ℃,最低-13.8 ℃。全年平均日照百分率为33%。5—10月份为降雨高发季,11月—次年4月份为枯季,西部降水量一般比东部多150 mm,气温比东部低3~4 ℃。两者高差差距较大,地域差异性在气温、降水量等气象要素上较为明显。
1.2 岩溶隧道模型构建
为进一步明确鸡冠山隧道上覆岩溶发育情况,采用高密度电法和地质雷达探查了天坑落水洞至隧道围岩之间的下泄渗漏带分布状况,然后再综合区域工程地质条件实现了岩溶隧道地质模型的构建。
1.2.1 下泄渗漏带探查
下泄渗漏带探查采用高密度电法和地质雷达进行。其中,高密度电法采用四极法装置(电极排列)2维测量,反演深度约70 m。地质雷达采用的是意大利IDS公司的探地雷达,在隧道衬砌内壁扫描,每个测区测线长度约100 m,每个测区测线6条,共3个测区。测线布置如图2所示。

图2 勘探区域及测线布置Fig.2 Exploration area and survey line layout
根据高密度电法及探地雷达探测数据对鸡冠山隧道下泄渗漏带分布情况进行可视化处理,如图3所示。可知,测区内存在两条较大断层SE22°倾角52°,SE23°倾角59°,存在多处溶腔向下延伸至隧道涌水点,形成多处贯通性涌水带,结合地表洞室分布形成了空间多处通道,隧道建设及运营存在较大安全隐患。
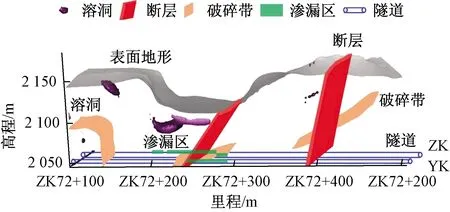
图3 测区空穴、破碎带、断层随隧道里程空间分布Fig.3 Distributions of karst cave, fracture zone, fault in the space
1.2.2 数值分析模型及边界条件
研究内容主要基于涌水资料数据以及积水水头边界条件,反演隧道上覆围岩的综合渗透系数。因此,模拟采用二维平面,隧道纵向取1 m。根据以往的经验和精度要求,隧道计算模型根据上一节地质物探成果及鸡冠山隧道设计的实际开挖尺寸确定建立。以鸡冠山隧道ZK72+220~ZK72+340下穿岩溶天坑段落水洞位置截取二维剖面,构建数值模型,隧道围岩赋予绿色属性,简化后的下泄渗漏带赋予蓝色属性,计算模型如图4所示。该模型宽320 m,高185 m,采用四边形网格剖分,共有网格单元7 021个,节点14 008个。
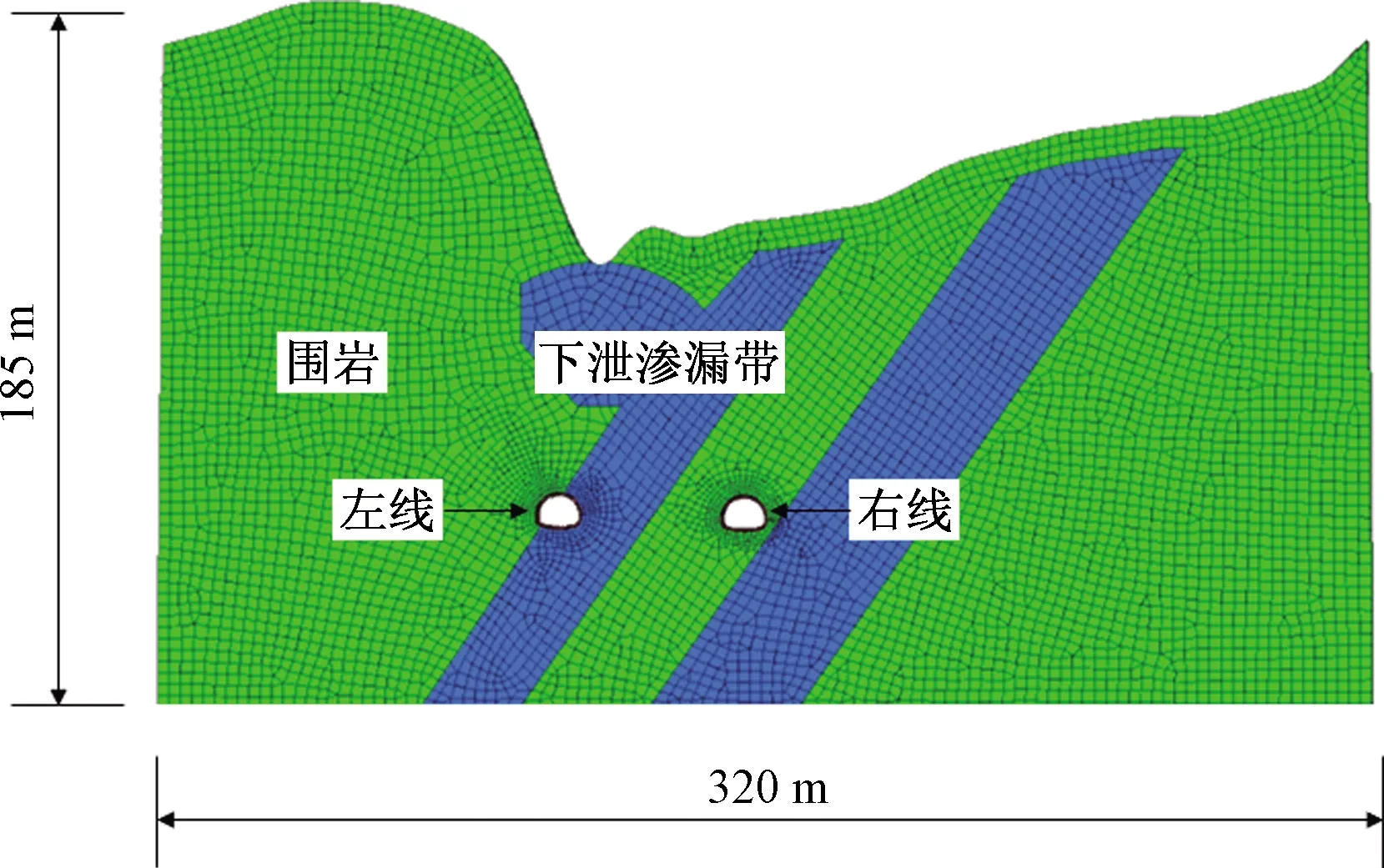
图4 计算模型Fig.4 Computational model
考虑到鸡冠山隧道岩溶天坑段上覆岩体存在落水洞,且溶腔周边存在断层及破碎带,降雨积水主要沿岩体溶蚀通道及裂隙扩散,因此,采用达西饱和渗流模型开展数值模拟。为方便试算,参考地质手册中建议的关于岩溶地区岩体渗透系数的取值范围1×10-4~1×10-2cm/s,岩溶溶腔下渗通道初始渗透系数取5×10-3cm/s,隧道围岩区初始渗透系数取5×10-4cm/s。衬砌的渗透系数参数依据工程设计取1.0×10-10cm/s。模型边界条件:x方向的边界x=0和x=320固定,y方向的边界y=0和y=1固定,z方向的边界为z=0,z方向上边界延伸至地表。模型左右及底边界默认为不透水固定位移边界,地表水头边界以天坑汇水计算确定的天坑地表降雨积水深度为准。并参考涌水报告考虑地下水位情况,模型初始设置以模型底边界向上40 m作为地下水位线。
2 最小二乘-分步耦合优化反演
基于以上数值模型的建立,拟采用反演分析方法确定岩溶岩体渗透系数。当前,岩土体渗流参数识别主要可分为直接法和间接法两类[22]。其中,直接法主要是借助边界条件求解基于控制方程(Darcy定律)的含待识别参数的线性一阶偏微分方程来获得渗透参数,但其前提是整个渗流研究区域的水头导数必须已知;间接法则是通过假定渗透参数初值,然后通过正演分析获得渗流特征量,再将其与实测值进行对比,如不符合实际情况,则调整参数,重新计算,直至符合要求。显然,间接分析法可适用于监测数据较少的情况,且不需要计算监测点数据的微分。当然,间接分析法也存在求极小化残差过程的非线性问题,但该问题可通过许多优化方法得以解决,如经典高斯-牛顿法、正则化最小二乘法、最小二乘支持向量机、人工神经网络等。其中,最小二乘是通过最小化误差平方和寻找数据的最佳函数匹配,较为方法简便。
最小二乘法目标函数为
minE=[hc-hm]T[hc-hm]
(1)
式(1)中:hc为计算矢量,hc={hc1,hc2,…,hcm};hm为观测矢量,hm={hm1,hm2,…,hmM},M为观测点数目与观测次数之积。若假设T为所求参数矢量,T={T1,T2,…,TL},L为要识别参数维数,对于非约束极小化问题,其高斯-牛顿迭代公式为
TK+1=TK-DK,K=1,2,3,…
(2)
AKDK=GK,K=1,2,3,…
(3)
式中:AK=JTJ(L×L),GK=JK[hc-hm](L×1);J为M×L阶Jacobian矩阵;D为Gauss-Newton方向矢量。
需要注意的是,当系数矩阵A奇异时,D矩阵构造将破坏,当系数矩阵A病态时,式(3)的解将严重失真。采用正则化处理可有效解决这一问题。正则化最小二乘方程为
(AK+_I)DK=GK
(4)
式(4)中:_为正则化因子;I为单位矩阵。

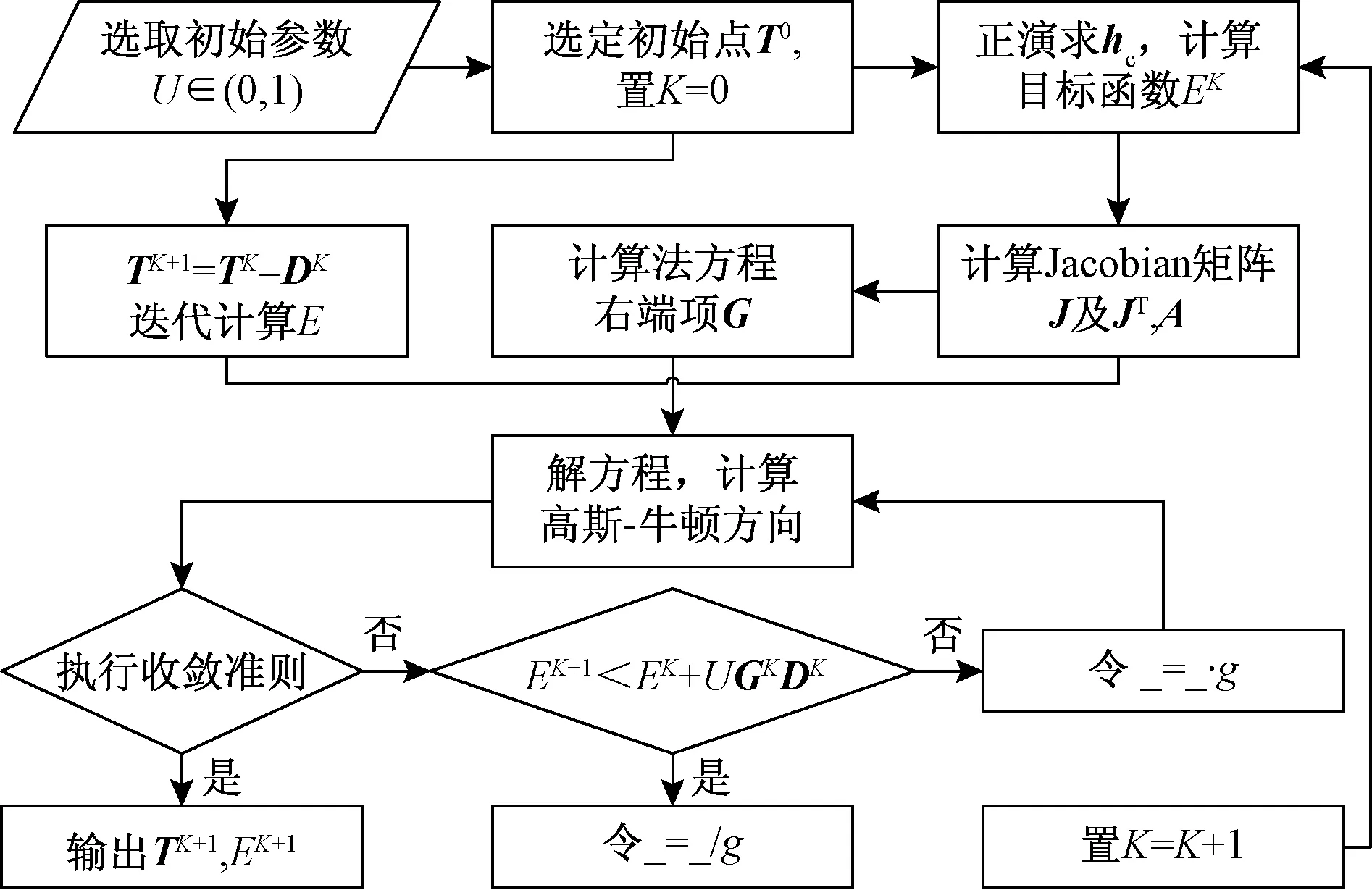
图5 正则化最小二乘反分析流程Fig.5 Flow chart of regularized least square inverse analysis
因此,采用基于最小二乘-分步耦合优化方法的岩溶隧道围岩渗流参数反演法。以3个涌水事件的涌水量、涌水速率、涌水与降雨关联时间、天坑积水水头为反演边界条件,降雨发生至涌水出现的间隔时间与隧道涌水速率作为反演搜索的关键指标,关联性解耦下泄渗漏带与隧道围岩渗透参数。下泄渗漏带渗透参数主要控制降雨发生至隧道涌水出现的间隔时间;下泄渗漏带渗透参数与隧道围岩区渗透参数的综合渗透效应控制隧道涌水速率。故反演的流程可按照两阶段展开。
3 岩体渗透参数反演分析
3.1 参数反演依据
依据隧道涌水与降雨关系分析,下穿岩溶天坑鸡冠山隧道段的降雨下渗路径与隧道涌水时间主要由下泄渗漏带渗透系数来控制。反演边界条件如表1所示,并以降雨发生至涌水出现的间隔时间与隧道涌水量作为关键反演指标。图6为涌水流量与压力监测点位置。

表1 隧道下穿天坑洞段的涌水事件反演指标表Table 1 Inversion index of water inrush event of tunnel underlying karst sinkhole
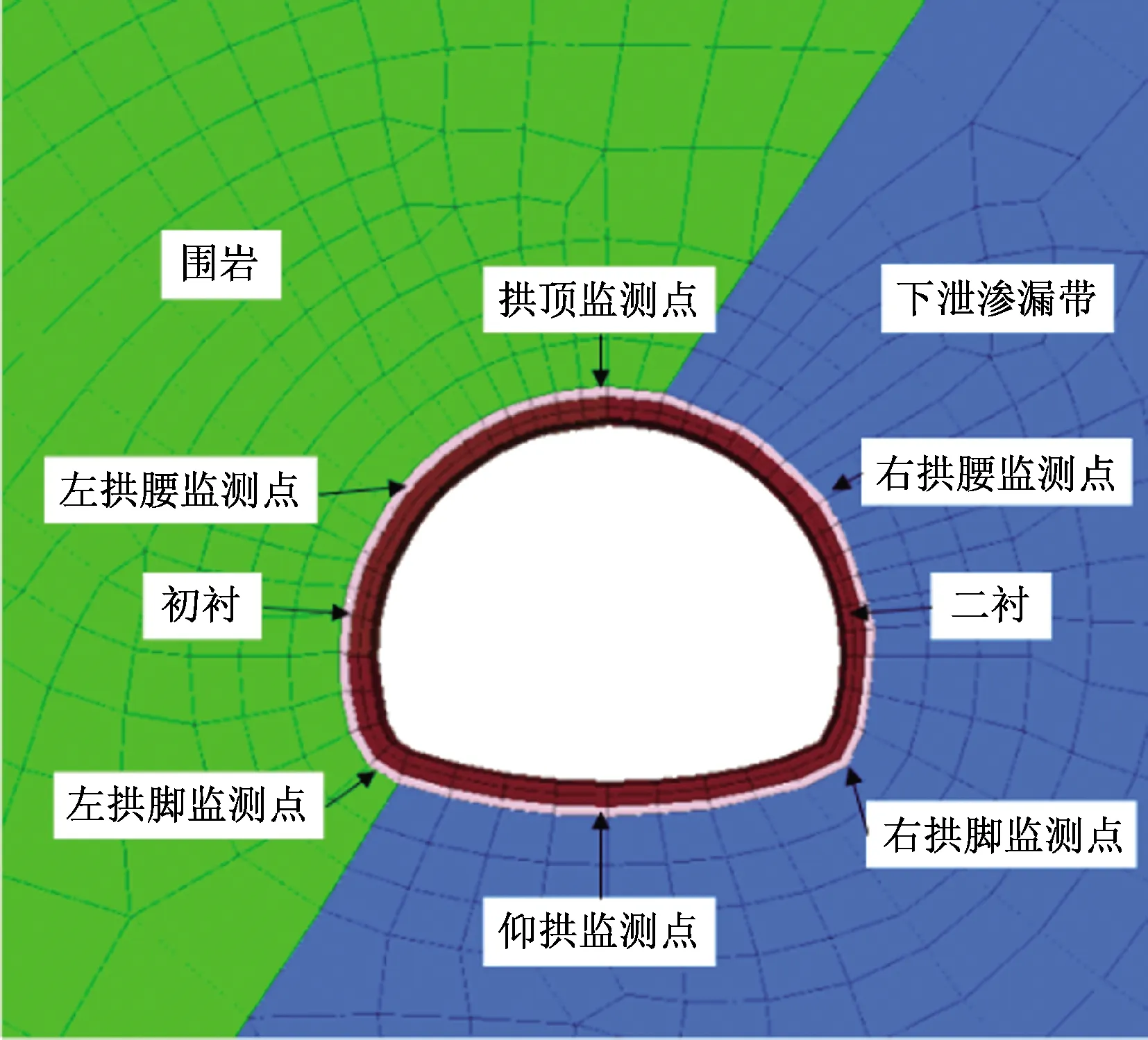
图6 左线水头压力监测点示意图Fig.6 Schematic diagram of monitoring points about water pressure on the left tunnel
为综合考虑降雨涌水时间间隔和隧道涌水量影响,关联性解耦下泄渗漏带与隧道围岩渗透参数,从而采用两步反演法开展岩溶岩体渗透参数分析,即首先以降雨发生至涌水出现的间隔时间为判定标尺,设计大量计算样本开展正演分析,初步确定各地层渗透系数反演参数取值区间;然后以隧道涌水速率为判定标尺,分步优化所得下泄渗漏带和隧道围岩区的渗透参数。具体流程如图7所示。

图7 渗透系数反演分析流程图Fig.7 Flow chart of permeability coefficient inversion analysis
3.2 涌水规律分析
隧道涌水规律与上部岩溶地层性质密切相关,寻找合理渗透参数取值区间则是获得理想反演结果的前提。本文隧道涌水渗流数值模拟采用有限差分FLAC3D软件进行,地表水头边界以天坑汇水计算确定的天坑地表积水深度为准。考虑到实际降雨半小时隧道即出现涌水,因此,以0.5 h作为判定标尺。
分别对照涌水事件1、2、3开展隧道涌水渗流数值模拟。隧道左洞监测点水头压力曲线如图8所示,处于下泄渗漏带的左线右拱腰位置的水头压力在0.5 h左右率先开始增加,其他监测点位置的水头压力在随后才开始增加,因此,以左线右拱腰位置的水头压力开始增加的时间作为降雨发生至涌水出现的间隔时间。
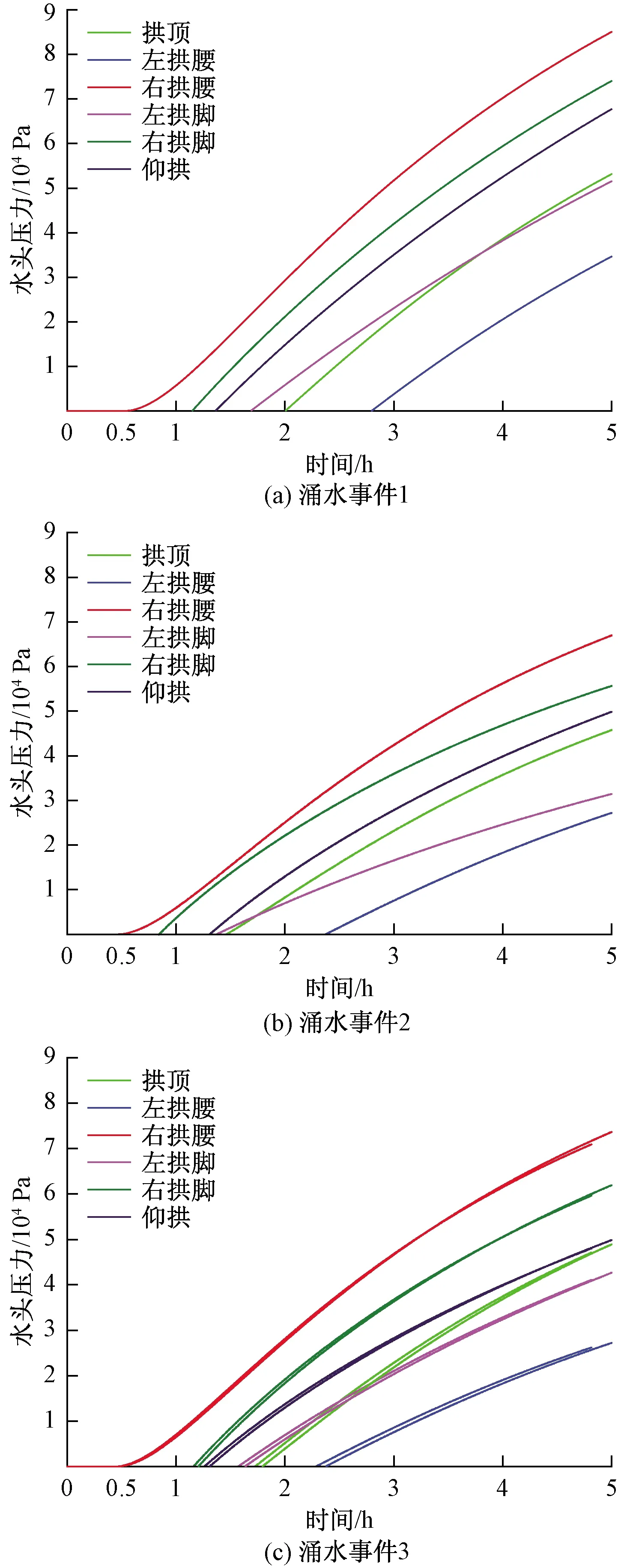
图8 涌水事件隧道左线监测点水头压力曲线图Fig.8 Changes of pore water pressure at monitoring points in left tunnel during water gushing
图9所示为3个涌水事件渗流5 h后的涌水压力分布,显然,处于下泄渗漏带侧的隧道涌水压力要大于另一侧。图10所示为3个涌水事件隧道涌水量速率曲线。经多次试算,计算峰值涌水速率与实际涌水峰值吻合时的下泄渗漏带渗透系数在1×10-3~3×10-3cm/s,隧道围岩的渗透系数在1×10-4~3×10-4cm/s。
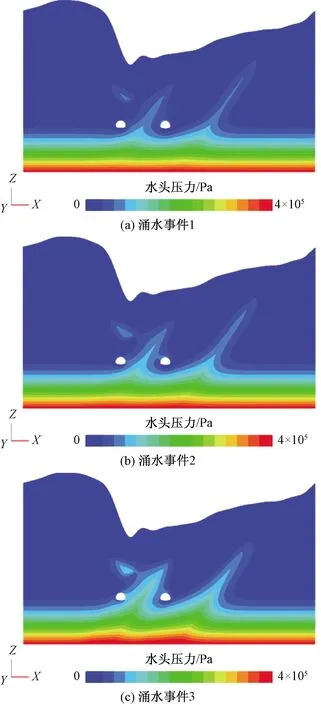
图9 涌水事件水头压力分布Fig.9 Distribution of pore water pressure during different water gushing events
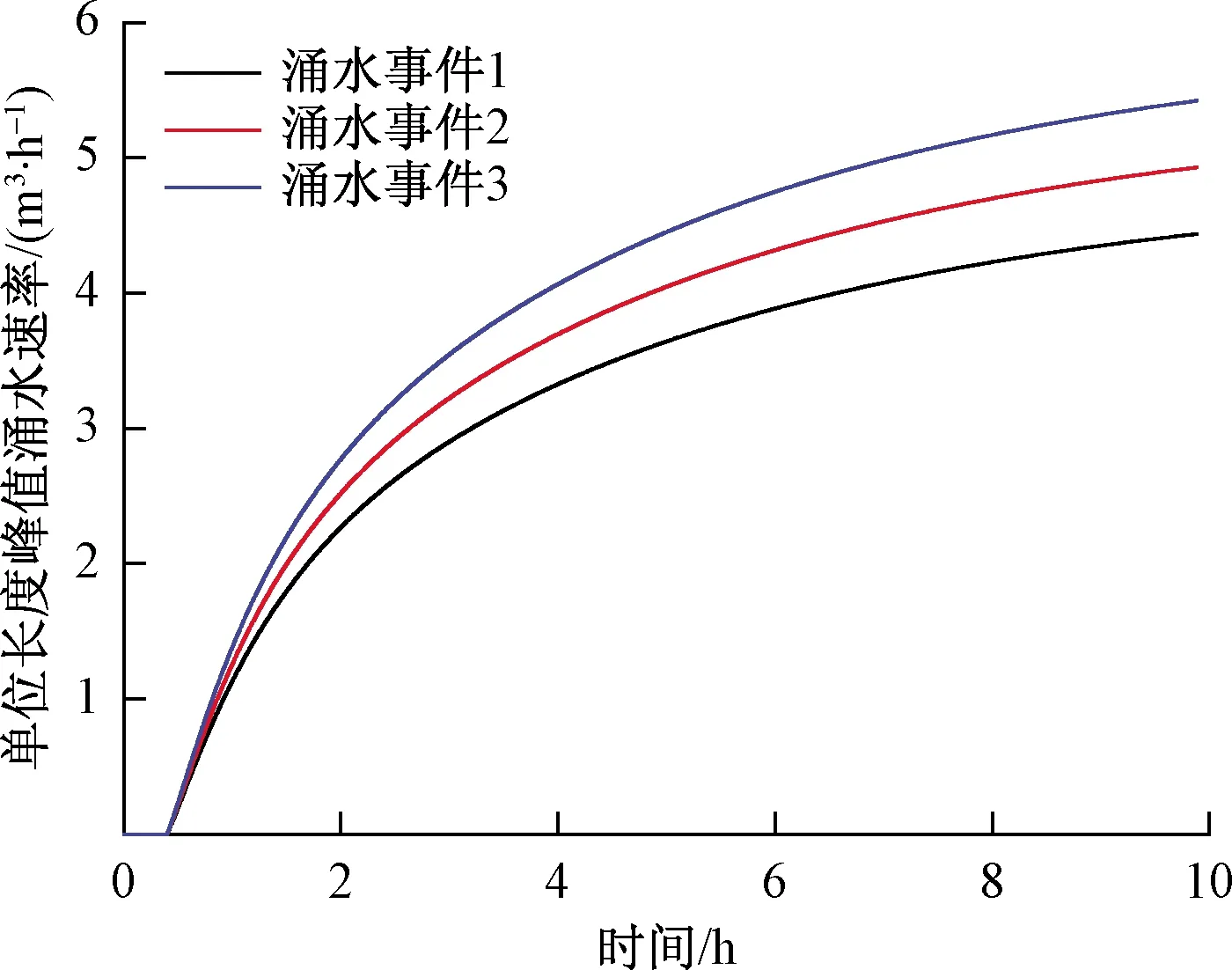
图10 涌水事件涌水速率曲线Fig.10 Curves of water gushing rate
3.3 渗透系数反演
为进一步保证反演参数的准确性,采用逐步扫描法来优化渗透参数取值。简单起见,以计算下渗时间与实际涌水事件中隧道收集到水的时间,数值模拟的隧道左线涌水速率与实际涌水事件中涌水速率的差值构建目标函数,即
(5)
(6)
式中:k1为下泄渗漏带渗透系数;k2为隧道围岩渗透系数;N为样本总数;xt为第t次涌水事件的计算下渗时间;Xt为第t次实际涌水事件中隧道收集到水的时间;yt为第t次涌水事件涌水速率;Yt为第t次实际涌水事件中单位长度左洞涌水速率。
3.3.1 下泄渗漏带渗透系数反演
以涌水事件1为始,下泄渗漏带渗透系数基准值取1×10-3cm/s,然后同步增加或减少k1,每次计算步长为1×10-4cm/s,最终获得下泄渗漏带渗透系数k1与f(k1)的关系曲线如图11(a)所示,对应左线右拱腰监测点涌水压力如图12(a)所示。显然,目标函数值随下泄渗漏带渗透系数增加先降后升。当目标函数最小时,所取的下泄渗漏带渗透系数与实际渗透系数越接近,因此,下泄渗漏带渗透系数最终可确定为1.3×10-3cm/s。同理,可以涌水事件2和3进一步修正下泄渗漏带渗透系数。以涌水事件1所得下泄渗漏带渗透系数取值为基准,以1×10-4cm/s为扫描步长进行数值模拟,所得涌水事件2和3下泄渗漏带渗透系数k1与f(k1)的关系曲线如图11(b)和图11(c)所示。对应的左线右拱腰监测点涌水压力曲线如图12(b)和图12(c)所示。可知,下泄渗漏带渗透系数分别为1.4×10-3cm/s和4.5×10-3cm/s。为减小误差,对3个涌水事件反演出的下泄渗漏带渗透系数求平均值,计算所得渗透系数2.4×10-3cm/s,即下泄渗漏带渗透系数。
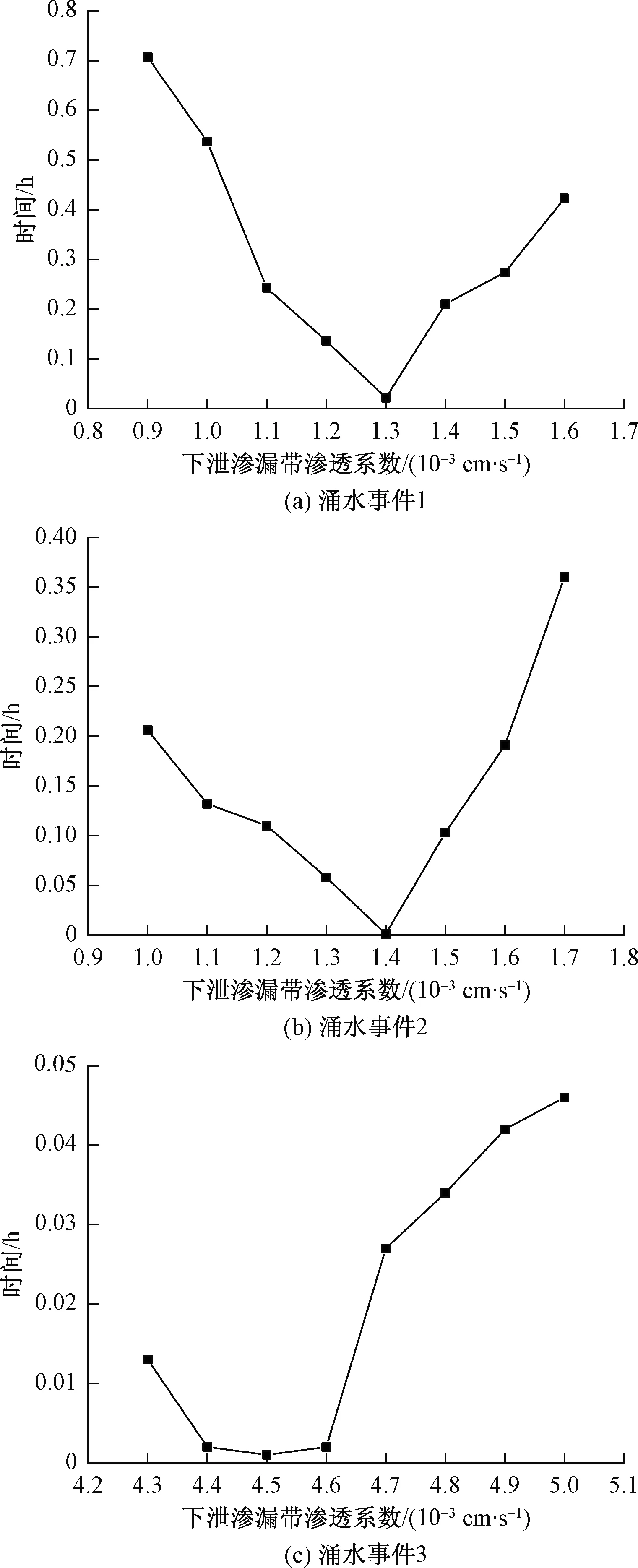
图11 目标函数与反演渗透系数关系Fig.11 Relationship between objective function and permeability coefficient of water infiltration zone
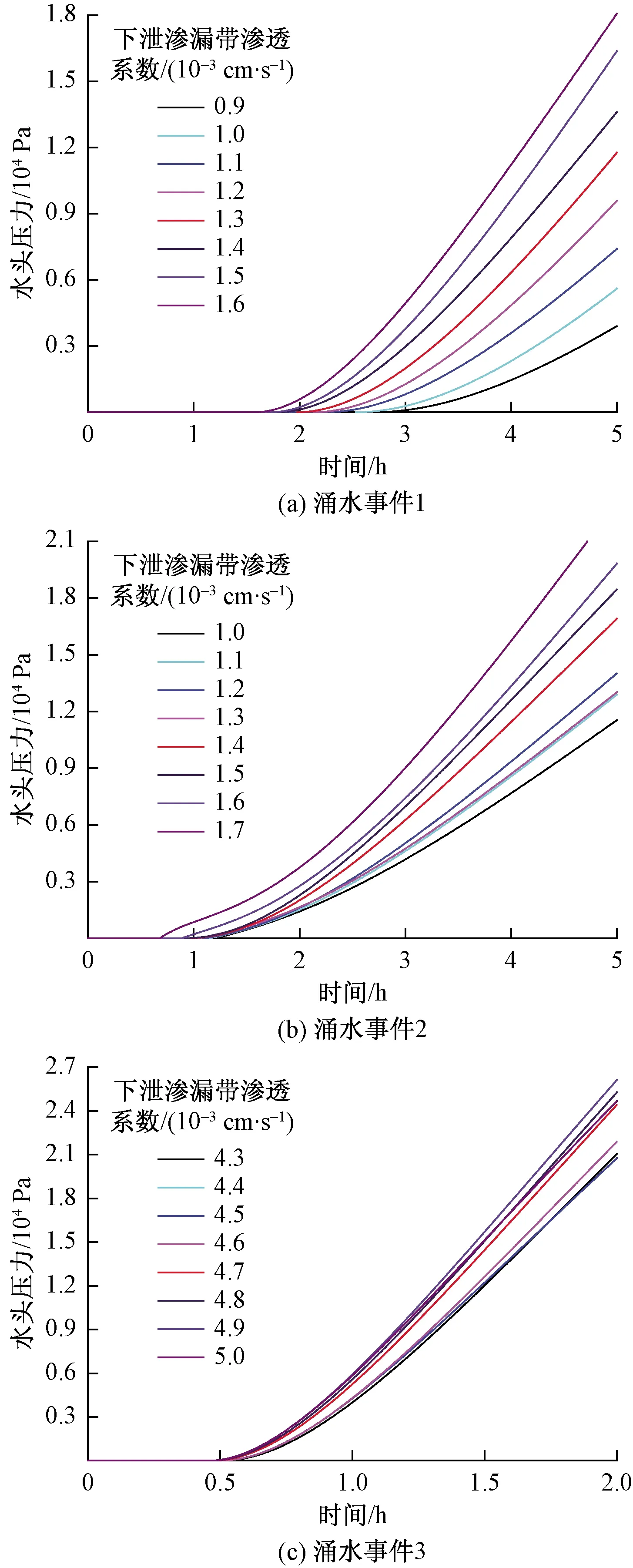
图12 左线右拱腰监测点孔压变化曲线Fig.12 Water gushing pressure of monitoring points at the right arch lumbar of the left tunnel
3.3.2 反演隧道围岩渗透系数
采用相同分析步骤,开展隧道围岩渗透系数反演。具体实施时,依次涌水事件1、2、3为依据,隧道围岩渗透系数基准值取1.3×10-4cm/s,然后同步增加或减少k2,每次计算步长为0.2×10-4cm/s,获得隧道围岩渗透系数k2与f(k2)的关系曲线和对应单位长度隧道峰值监测涌水速率曲线,如图13、图14所示,确定三次涌水事件所对应的隧道围岩渗透系数如表2所示。为减小误差,对3个涌水事件反演出隧道围岩渗透系数求平均值,所得渗透系数3.2×10-4cm/s,即为隧道围岩渗透系数。

图13 目标函数与隧道围岩渗透系数关系Fig.13 Relationship between objective function and permeability coefficient of surrounding rock mass

图14 单位长度隧道峰值监测涌水速率Fig.14 Peak water gushing rate in the left tunnel within unit length

表2 隧道围岩渗透系数表Table 2 Table of permeability coefficient of surrounding rock of tunnel
4 结论
鸡冠山岩溶隧道涌水量主要受下泄渗漏带的渗透系数控制,合理确定隧道围岩渗透参数是估计隧道涌水量与防排水设计的关键。釆用综合勘察法得到鸡冠山隧道区工程地质条件和水文地质条件、岩溶天坑的下泄渗漏带位置,构建饱和达西渗流计算模型,然后,以3个涌水事件对应的积水水头边界、降雨涌水时间差及涌水速率为依据,采用最小二乘-分步耦合优化方法反演岩体渗流参数,最终获得下泄渗漏带渗透系数建议取值为2.4×10-3cm/s、隧道围岩渗透系数取3.2×10-4cm/s,可为后续降雨条件下岩溶隧道衬砌结构安全性分析研究提供参数取值依据。

