基于PHAT-β广义互相关的变压器机器 鱼避障时延估计仿真
张 弛, 刘力卿, 魏菊芳, 唐庆华, 王 楠,季洪鑫
(1.国网天津市电力公司电力科学研究院, 天津 300384; 2.天津市电力物联网企业重点实验室, 天津 300384;3.国网天津市电力公司,天津 300010; 4.清华大学航天航空学院, 北京 100084)
长期以来变压器内部故障一直存在难以及时发现、检测和定位的问题,对电网的安全运行造成了巨大的隐患[1]。常规的局部放电检测法和油中溶解气体分析法虽然能够在一定程度上对变压器的故障进行判断,但是在故障类型识别、故障位置快速定位等方面依然存在一定的局限性[2]。近年来,随着微型机器人技术和人工智能算法的进步,通过机器鱼进入变压器内部进行故障检测引起了中外学者的关注。2018年,ABB公司首次提出了油浸式变压器内部巡检机器人,概述了变压器机器人的设计理念、运行原理和技术创新性[3]。国家电网天津电力科学研究院王伟等[4]分析了采用机器鱼进行变压器内部巡检的优势和可行性,指出微型机器鱼具有体积小、能运动、能感知的优点,能够直观准确地对变压器内部故障和绝缘劣化程度进行检测。由于变压器内部设备组件多,检测过程中必须要保证机器鱼不能与变压器内部组件发生碰撞,因此,避障是机器鱼在检测过程的需要重点考虑的问题之一。刘力卿等[5]对变压器机器鱼的避障路径规划开展了研究,提出了基于人工势场法和蚁群算法的路径策略,通过仿真获得了较短的无碰撞路径。针对变压器内部环境具有电磁干扰大、黑暗无光照的特点,通过发射超声信号和接收反射回波信号进行时延估计是一种行之有效的避障方法。
超声回波避障的核心是发射信号和回波信号的时延估计。目前,时延估计算法在许多领域具有重要的应用,如通信传输、声呐探测、地质勘探、泄漏定位等领域[6-9]。根据不同应用场景的信号特征,经典的时延估计方法主要包括:上升沿触发法、阈值触发法和互相关方法等[10-12]。其中,上升沿触发法和阈值触发法是计算量最小的时延估计方法,一般只适用于波形轮廓清晰、波形无畸变或畸变较小的场合;互相关方法通过互相关函数的峰值检测实现时延估计,具有运算快速、鲁棒性好等优势,能够应对一定程度的波形畸变,是目前适用最广泛的时延估计方法。但是随着现代检测领域噪声成份越来越复杂,波形畸变越来越严重,时延估计的难度也越来越大。为了提高时延估计的性能,Knapp等[13]在基本互相关的基础上提出了广义互相关算法,通过对信号进行预白化处理,可以起到锐化互相关函数曲线、提高时延估计性能的作用。金中薇等[14]对几种不同的广义互相关加权函数PATH、ROTH 和 SCOT进行了对比,分析了其时延估计特性和定位误差。Bhardwaj 等[15]分析了信号中噪声的相关性,提出了一种采用最大似然方法进行多声道时延估计方法。徐海涛等[16]针对强噪声情况下语音定位时延估计的精度较低的问题,提出基于维格纳-威利分布(Wigner-Ville distribution) 的一次与二次相关时延估计算法,并且通过仿真验证了该方法的有效性。张亚斌等[17]针对海洋探测中信号信噪比低导致时延估计精度低的问题,提出一种基于二次相关和高阶累积量的时延估计方法,结果表明该方法具有抑制多种噪声的能力。王阳等[18]针对时延估计中信号起振点难以准确获取的问题,提出了一处基于短时能量拟合曲线的起振点估计算法,该方法通过信号能量突变寻找包含信号起振信息的时间窗,提高了时延估计精度,减小了到达时间差的估计误差。虽然现有的时延估计算法可以在很大程度上提高时延估计的性能,但是这些方法往是针对特定的应用场景和信号特征,而且时延估计时所采用的计算参数往往是固定的,无法根据信号的变化进行调节,因此适用性受到一定的限制,目前还难以在机器鱼实时避障领域进行应用。
因此,针对变压器内部电磁干扰强烈、噪声情况复杂等情况,提出一种基于相位变换加权(PHAT-β) 广义互相关(GCC)算法、并且参数可调的变压器机器鱼避障时延估计方法,分析了不同信噪比、不同发射超声信号类型以及不同β指数调节因子对时延估计性能的影响。
1 机器鱼避障原理和变压器油中声传播
机器鱼体上安装有收发一体化的超声探头和信号处理器,通过发射超声信号、接收反射回波信号、时延估计算法实现机器鱼的避障功能。一旦机器鱼距离障碍物的时延值接近于机器鱼的制动时间,机器鱼就要进行制动或者转弯操作从而避免发生碰撞事故。机器鱼结构示意图如图1所示。
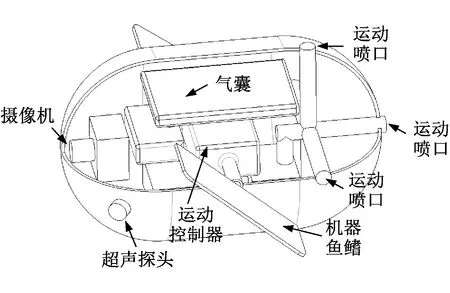
图1 变压器机器鱼示意图Fig.1 Schematic diagram of transformer robot fish
机器鱼发射的超声信号在变压器油中传播,传播过程为波动过程,根据初始条件和边界条件对波动方程求解,能够获得声波的振幅和相位等信息。流体中波动方程一般由状态方程、连续方程和运动方程进行推导得到。运动方程表示为

(1)
根据质量守恒定律,连续性方程可表示为
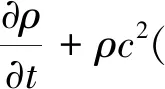
(2)
式中:u为质点振动速度;p为声压;ρ为变压器油密度;c为声速。
由于流体不能承爱剪切力,根据式(1)和式(2)可以得到声压p的微分方程为
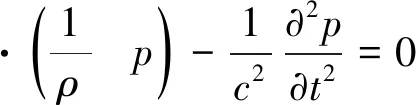
(3)
由于短时间内变压器油的密度是恒定均匀的,声压p的波动方程可以表示为

(4)
因此声场中任意位置处的声压的通解可以表示为
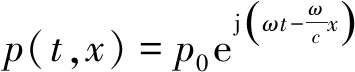
(5)
式(5)中:p0为声源处的声压;ω为角频率。
2 时延估计算法
假设机器鱼发射和接收的超声信号分别为x1(n)和x2(n),其表达式分别为
x1(n)=s(n)+n1(n)
(6)
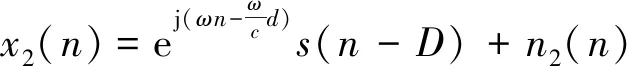
(7)
式中:s(n)为无噪声正弦信号;n1(n)和n2(n)为系统噪声;D为时延值;d为信号传播距离。
变压器油中超声信号的信噪比(signal-noise ratio, SNR)定义为
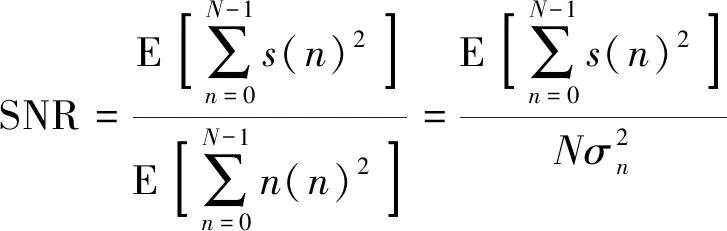
(8)
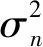
2.1 基本互相关(BCC)时延估计
基本互相关的计算公式为
Rx1x2(τ)=E[x1(n)x2(n+τ)]=

(9)
式(9)中:τ为时间延迟,Rx1x2(τ)表示互相关函数;E表示期望函数;T表示信号采样时长。将式(6)和式(7)代入式(9)可以得到
Rx1x2(τ)=E[x1(n)x2(n+τ)]=
s(n-D+τ)+n2(n+τ)}=
Rsn1(τ-D)+Rsn2(τ)+Rn1n2(τ)
(10)
式(10)中:Rss(τ-D)为信号s(n)的自相关函数的偏移;Rsn1(τ-D)和Rsn2(τ)为信号和噪声的互相关函数;Rn1n2(τ)为噪声和噪声的互相关函数。
一般情况下,信号与噪声、噪声与噪声之间是弱相关或不相关,因此可以假设
Rsn1(τ-D)=Rsn2(τ)=Rn1n2(τ)=0
(11)
则式(10)可以简化为
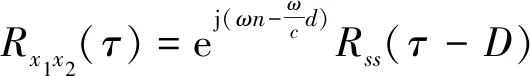
(12)
由式(12)可以看出:Rx1x2(τ)在τ=D时取得最大值,即通过基本互相关函数曲线的峰值检测即可实现信号的时延估计。基本互相关时延估计流程如图2所示。
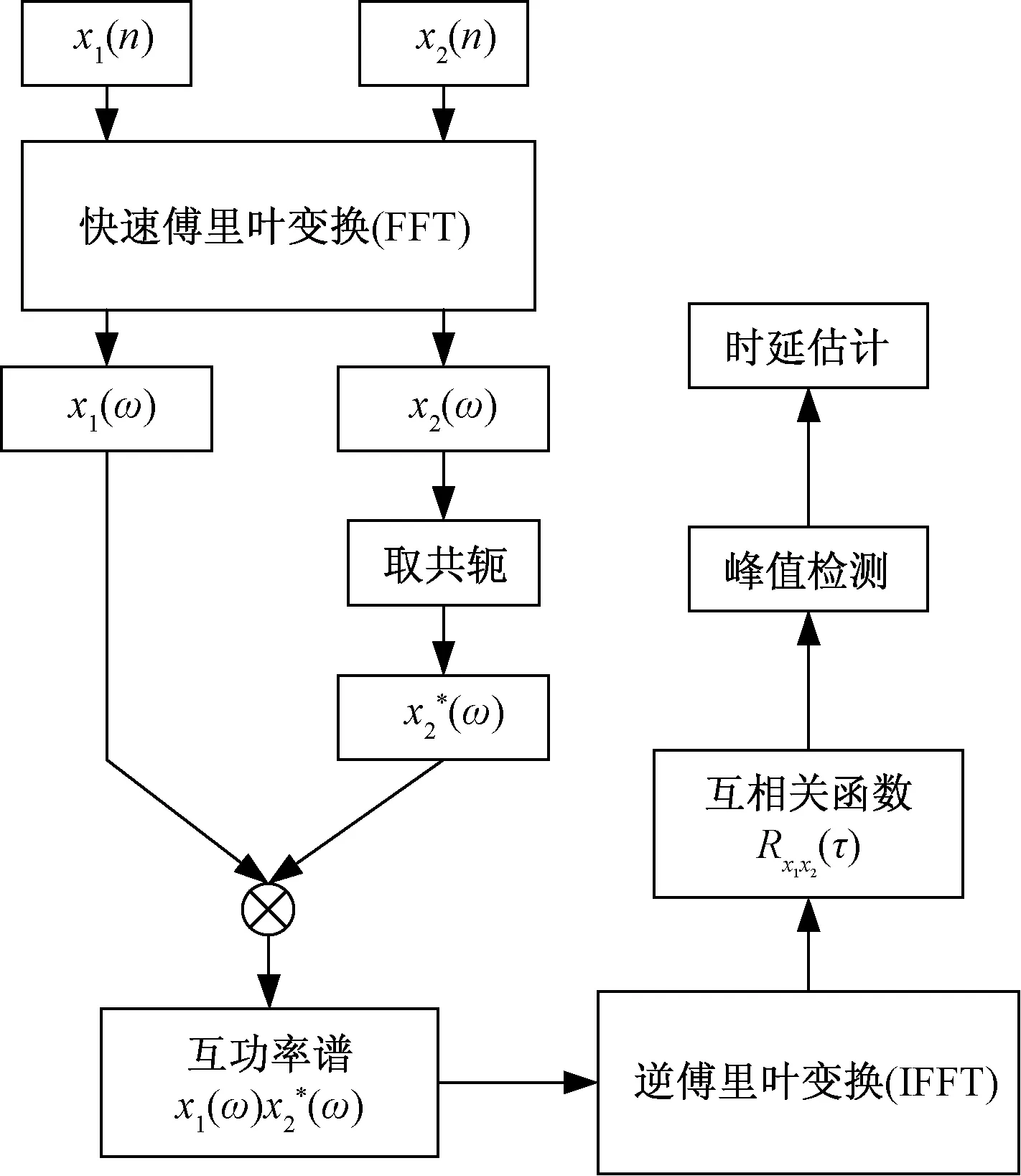
图2 基本互相关计算流程图Fig.2 Flow chart of basic cross correlation
2.2 PHAT-β GCC时延估计
实际测量系统中,噪声之间一般不是严格意义上的不相关,即Rsn1(τ-D)、Rsn2(τ)和Rn1n2(τ)通常不绝对为0,因此,基本互相关时延估计的准确性会受到噪声的影响。在基本互相关的基础上,通过在频域内对互功率谱函数进行一定的加权,可以起到抑制噪声的目的,加权的作用等效于对信号进行预滤波处理。加权后的广义互相关函数表示为
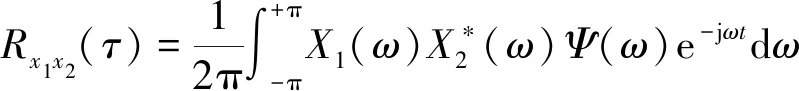
(13)
式(13)中:ψ(ω)表示加权函数,PHAT-βGCC的加权函数为
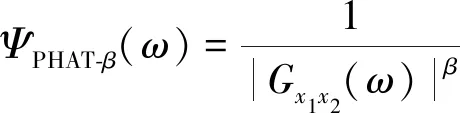
(14)
式(14)中:Gx1x2(ω)为发射和反射信号的互功率谱密度;β为指数调节因子,范围为[0,1]。
对PHAT-β加权之后的广义互相关函数进行峰值检测得到的时延估计结果为
τ′=argmaxRx1x2(τ)=
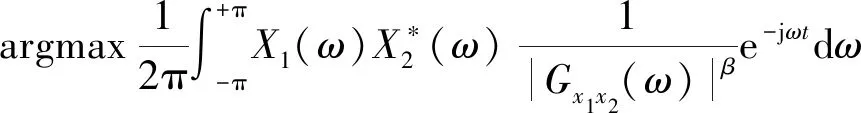
(15)
PHAT-βGCC时延估计流程如图3所示。
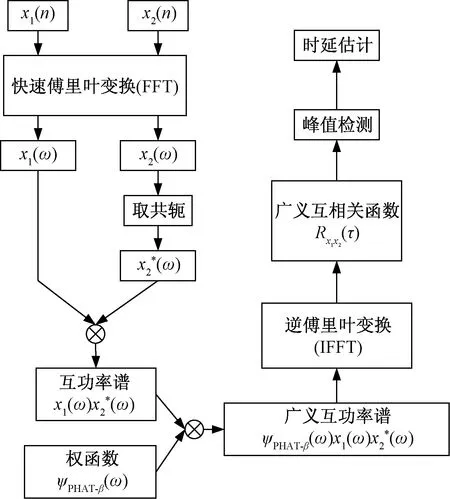
图3 PHAT-β GCC计算流程图Fig.3 Flow chart of PHAT-β GCC
采用PHAT-βGCC算法进行时延估计的优势在于:在基本互相关算法的基础上引入了权函数和指数调节因子,通过改变指数调节因子的取值可以对噪声信号进行不同程度的抑制,实现互功率谱密度的灵活调节。
3 仿真研究
3.1 超声发射信号
机器鱼发射的超声信号采用5个周期的正弦信号和方波信号,信号频率为100 kHz, 采样频率为2 MHz。两种信号的时域和频域波形如图4、图5所示。
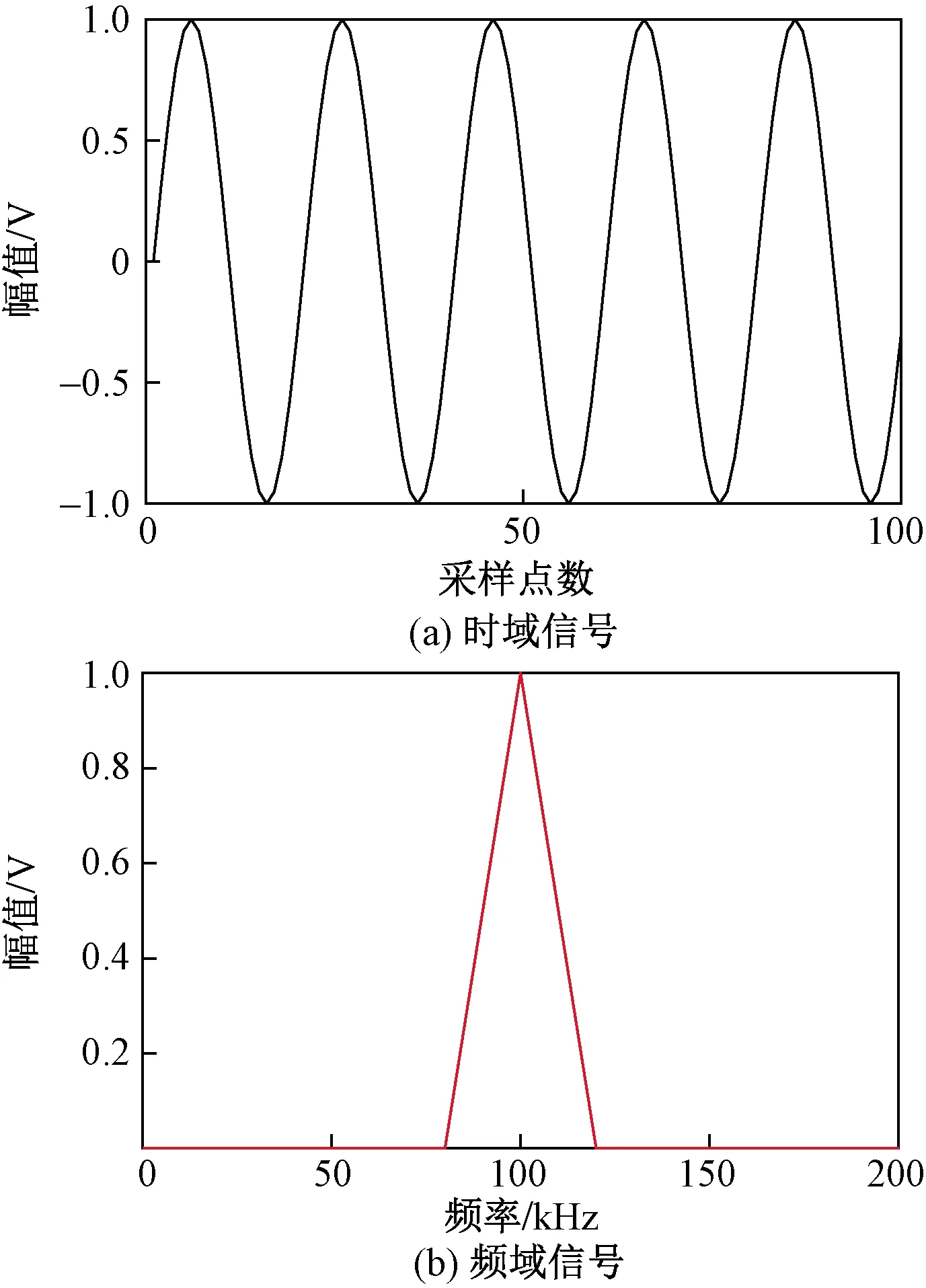
图4 正弦信号Fig.4 Sinusoidal signal
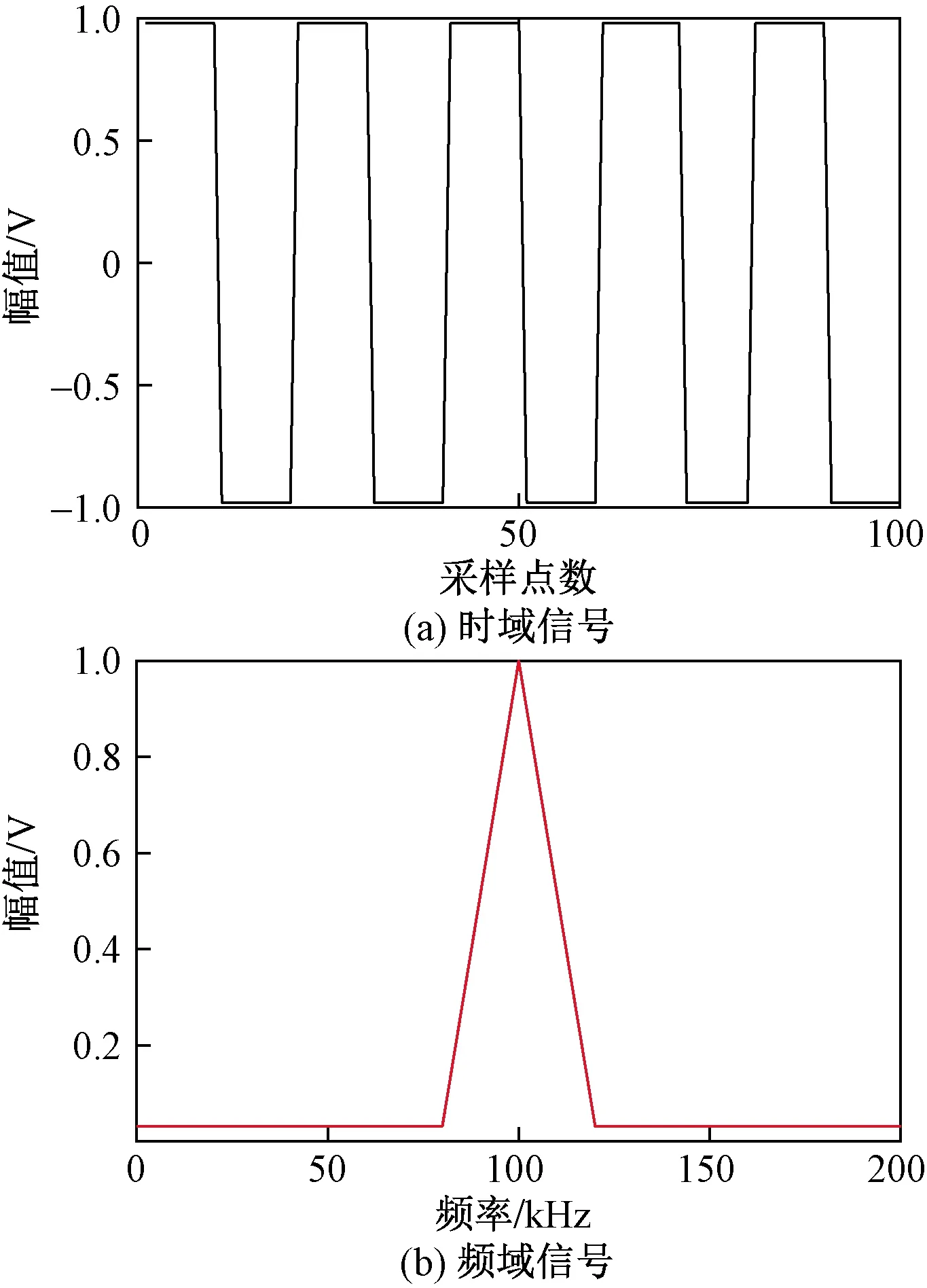
图5 方波信号Fig.5 Square signal
3.2 不同信噪比的超声回波信号
发射超声信号和反射回波信号之间的时延值设置为 50个采样点,回波信号的声压按照式(5)计算获得。当发射信号为正弦波时,不同信噪比(20、10、0 dB)的超声回波信号如图6所示;当发射信号为方波时,不同信噪比的超声回波信号如图7所示。
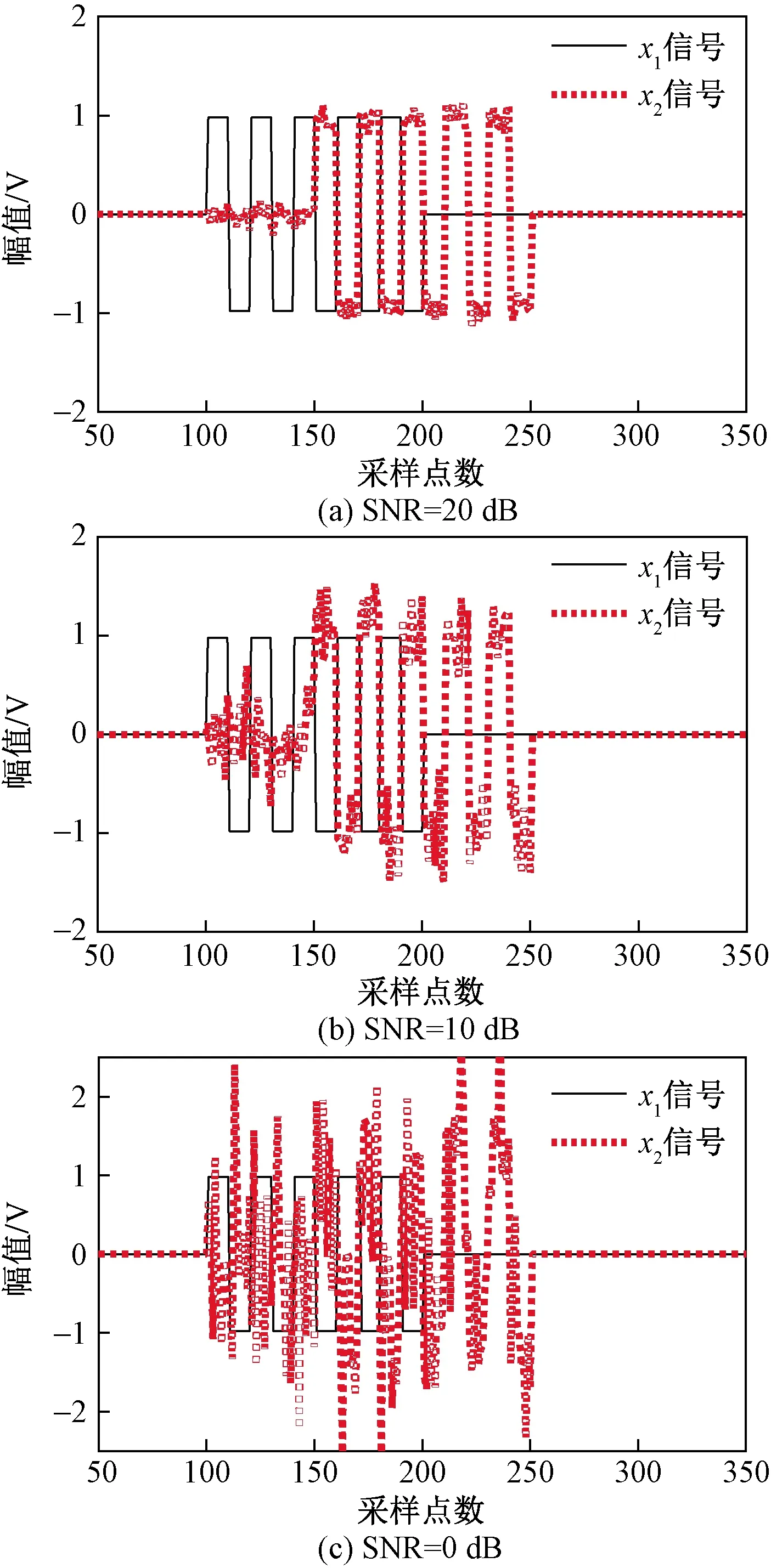
图7 不同信噪比方波发射信号和回波信号Fig.7 Square emission and echo signal with different SNR
通过图6和图7可以看出,随着信噪比的降低,不管发射信号是正弦波还是方波,反射回波信号的波形畸变逐渐变大,从而增加了时延估计的难度。
3.3 时延估计性能
为了验证PHAT-βGCC算法在不同噪声条件下的性能,分别针对正弦信号和方波信号进行了不同信噪比的时延估计仿真,并且比较了PHAT-βGCC算法与BCC算法的性能。
3.3.1 正弦信号时延估计结果
不同信噪比正弦信号时延估计结果如图8所示。图中纵坐标分别为互相关函数和广义互相关函数,范围为[-1, 1],是一个无量纲单位的常数。
当发射信号为正弦波时,纵向对比图8所示结果可以明显看出:随着信噪比的降低,BCC和PHAT-βGCC算法得到的曲线峰值越来越不明显,这说明噪声的加入降低了两种算法的时延估计性能。横向对比图8所示的结果可以明显看出:右侧PHAT-βGCC算法得到的曲线峰值比左侧BCC算法得到的曲线峰值要更加尖锐和明显,这说明PHAT-βGCC能够更准确地通过峰值检测实现时延估计,即PHAT-βGCC的时延估计性能优于BCC的时延估计性能。
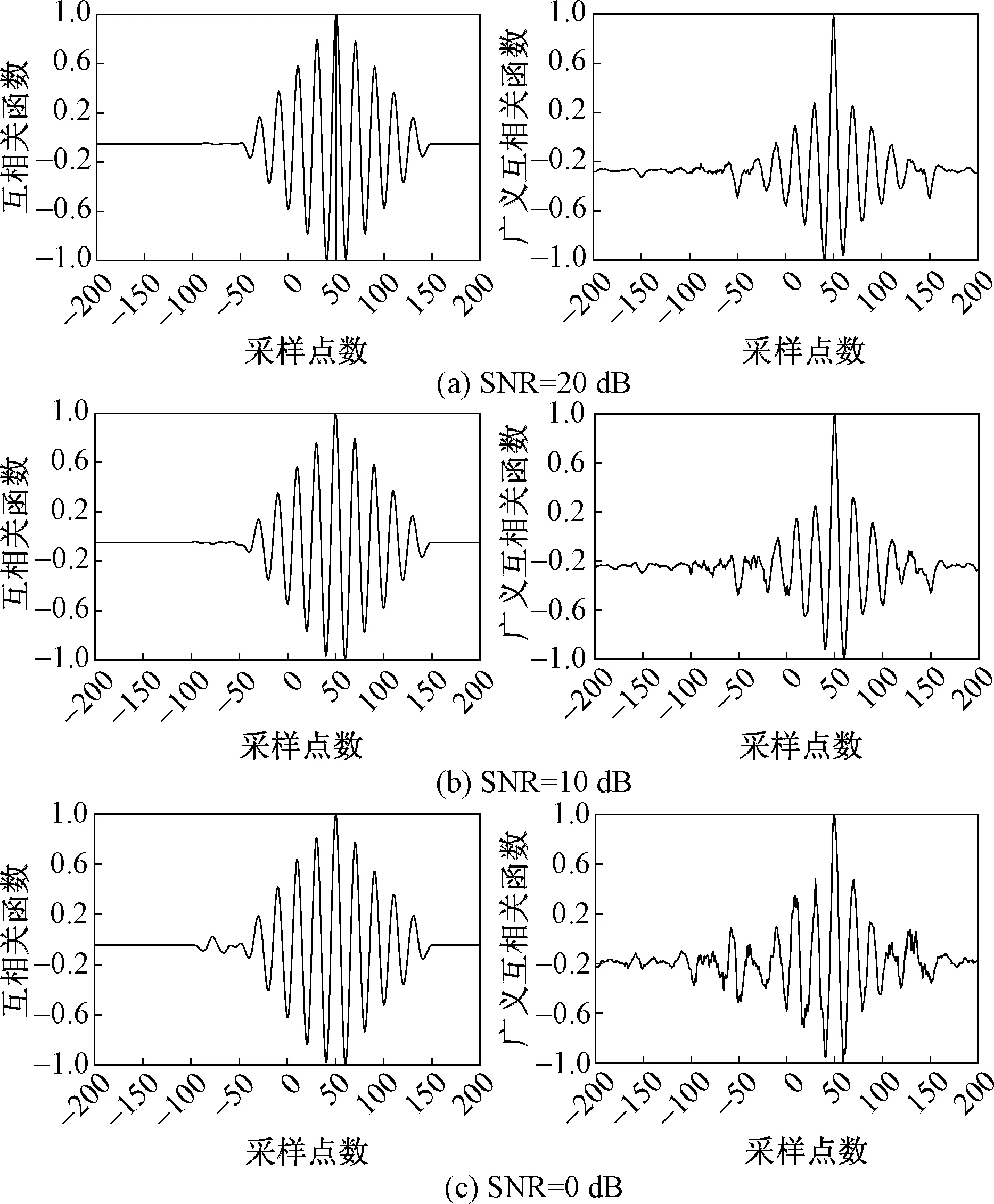
图8 正弦信号时延估计结果Fig.8 Time delay estimation results of sinusoidal signal with SNR=0 dB
3.4 方波信号时延估计结果
不同信噪比方波信号时延估计结果如图9所示。

图9 方波信号时延估计结果Fig.9 Time delay estimation results of square signal
通过对比图9可以看出:随着信噪比的增加,方波信号采用PHAT-βGCC算法得到曲线峰值同样比BCC曲线的峰值要尖锐和明显,同样验证了PHAT-βGCC时延估计性能优于BCC的结论。
综合对比正弦信号和方波信号的结果可以发现:采用方波信号的时延估计性能比正弦信号的时延估计性能要略好一些,如图8(c)和图9(c)所示。
为了验证PHAT-βGCC算法中指数调节因子β的取值对时延估计性能的影响,针对方波信号、信噪比为0 dB的条件,进一步分析了不同β取值的时延估计性能,如图10所示。
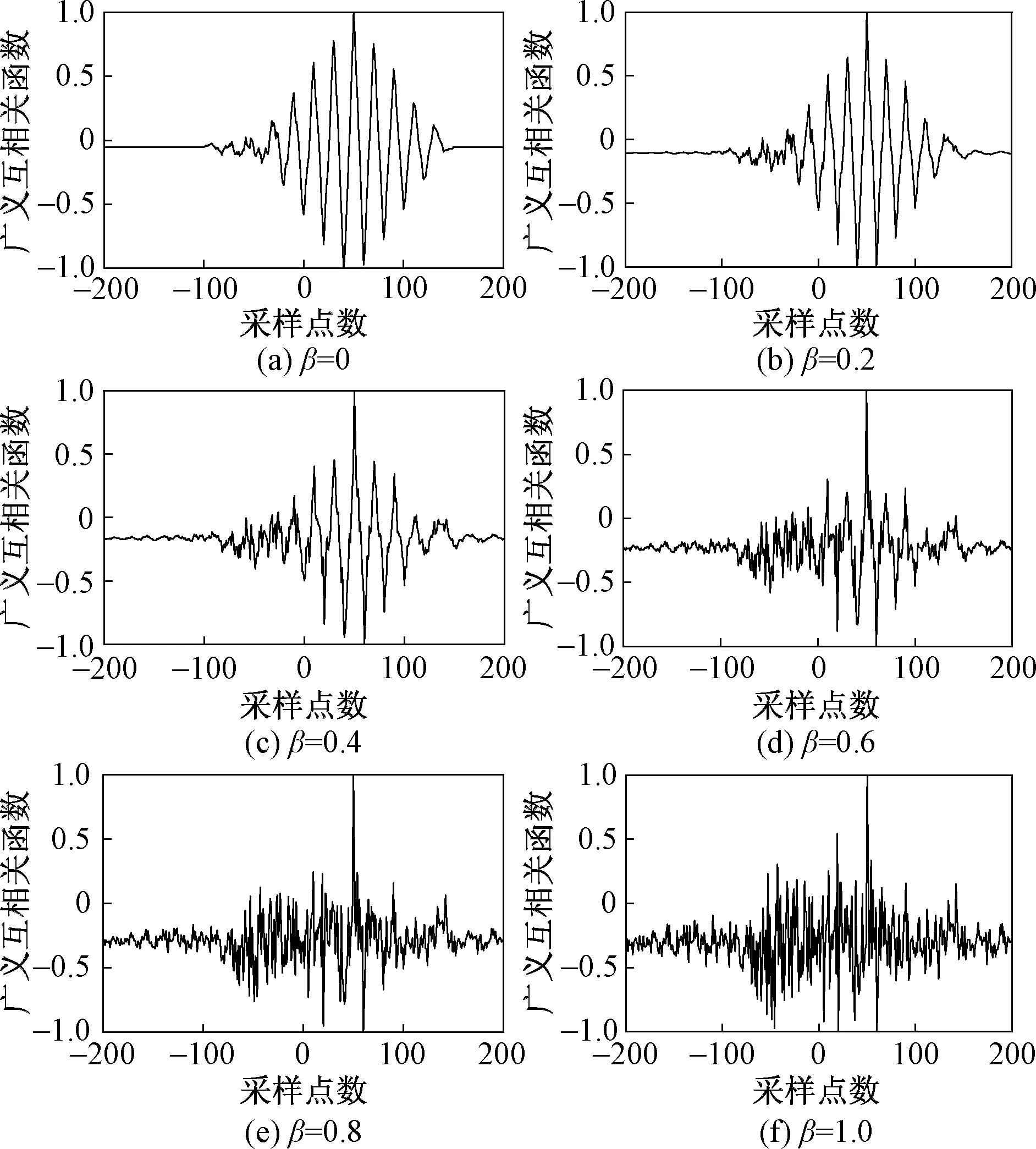
图10 不同β取值的时延估计结果Fig.10 Time delay estimation results with different β
通过图10可以看出,随着β数值的增大,时延估计性能先是逐渐变好,在0.6和0.8时时延估计结果最好,超过0.8之后时延估计结果又变差。因此,采用PHAT-βGCC算法进行时延估计时应要所信号特征和噪声条件选择最优化的β取值,针对仿真设置的信号和噪声特征,β的最优取值范围为[0.6,0.8]。
4 结论
针对变压器机器鱼时延定位和避障问题,提出一种基于PHAT-βGCC算法的变压器机器鱼时延估计方法。通过仿真对比分析了不同信噪比(20、10、0 dB)和不同类型超声信号(正弦信号、方波信号)的PHAT-βGCC时延估计性能,研究结果表明不管是正弦信号还是方波信号,采用PHAT-βGCC比BCC的时延估计性能更好;采用方波信号的时延估计结果比正弦信号的时延估计结果要好;不同信号特征条件下,PHAT-β广义互相关存在一个合适的β取值空间。

