顾及各向异性的多参数协同优化IDW插值方法

颜金彪，吴 波，何清华

1. 江西师范大学地理与环境学院，江西 南昌 330022； 2. 衡阳师范学院传统村镇文化数字化保护与创意利用技术国家地方联合工程实验室，湖南 衡阳 421002

在地学研究中，通常需要具有一定规则的面状数据。然而，很多可获得的地学数据都是站点采集的，呈现离散和不规则的分布[1]。这就经常需要利用空间插值技术将不规则的离散数据转换成规则的面状空间数据。

空间插值是通过有限的离散采样点来建立某种插值函数关系，并将待插值点一定范围内的已知采样点代入该函数表达式来获得该插值点的属性值[2]。常用的插值方法包括克里金插值方法、自然邻域法、趋势面法及反距离加权插值(inverse distance weighting,IDW)等。由于IDW插值原理简单、计算简便且符合地理学第一定律[3]，在各学科领域都得到了广泛应用[4-7]，被认为是GIS领域中一种标准的空间插值方法。尽管在多数情况下IDW插值方法都能取得较好的效果，但由于地学数据的复杂性，其插值效果还有待进一步提高。

近年来，人们从最邻近点数、距离衰减系数以及空间邻近度[8]等几方面提出了各种改进算法，改善了IDW空间插值精度及其适用性。在如何选择最邻近点数方面，文献[9]认为利用14个最邻近的点进行IDW插值是合适的，而文献[10]认为用5个最邻近点就可以得到满意的结果。其次，文献[11]在评估城市噪声地图时发现距离衰减系数α=4比α=1能获得更加准确的噪声分布地图；文献[9]认为不同的α值将有不同的插值结果，并建议通过多次试验来选择参数α。文献[10]认为在研究区内的不同地点可能存在不同的距离衰减关系，并开发了一种自适应IDW方法(AIDW)，允许参数α根据邻近采样点的空间模式变化。在算法参数的优化方面，现有方法或者仅考虑单参数对IDW插值的影响，或者依次对各参数进行独立优化，都难实现模型插值精度的整体优化。文献[7]固定距离衰减系数为2，利用交叉检验(cross validation，CV)[12]去优化得到最邻近点数；文献[9]固定最邻近点数为14，利用CV去优化距离衰减系数，但候选的距离衰减系数仅有3个可选值。考虑到IDW的插值精度受到多个参数的影响，部分参数独立调优难实现插值模型的整体优化，因此，实践上需要提供一种智能化程度较高的多参数协同优化方法。

经典的IDW假设地理事物的分布呈现各向同性[13]的特点，因而通常采用欧氏距离来表达空间邻近度。由于地理事物分布的复杂性，其分布往往呈现各向异性[14]的特点，如气温呈现出明显的经纬度方向性，使得各向同性的距离度量难以反映气温在经纬度方向的不同变化。文献[15]将欧氏距离转变为待插值点与参考样本点的最短路径距离来重新定义空间邻近度；文献[16]提出采用一种“椭圆”距离来处理各向异性的插值问题，文献[17]提出了一种基于最短风场路径的复杂距离来表征城市风场对颗粒物浓度分布的影响；针对河道各向异性的复杂地形，文献[18]采用最短时间距离来替代欧氏距离；顾及电离层分布的经纬度方向异性，文献[19]重新定义空间邻近性后获得了更高精度的电离层插值效果。目前已有的研究大多情况针对特定应用场景来改进算法，并通过重新定义空间邻近度来提高IDW的插值精度，需要额外的辅助数据(如风速、流速等)来定义各向异性的空间邻近度，制约了这类方法的普适性应用。

本文提出一种顾及空间各向异性的多参数协同优化IDW插值方法(PIDW)。首先，引入具有物理意义的距离及方向调节参数来反映地理现象的各向异性，将典型的欧氏距离扩展为各向异性的“椭圆”距离；然后，基于CV准则构造了适合于PIDW插值算法的适应度函数，并采用粒子群算法对PIDW插值模型的多个参数进行协同优化，实现PIDW插值效果最佳的目的。

1 PIDW算法

PIDW是一种顾及各向异性的IDW插值的改进模型，通过引入距离及方向调节参数来描述空间点间各向异性的邻近性关系，并利用粒子群优化算法实现模型的多参数协同优化。图1是PIDW方法的主要流程，其算法主要包括四参数协同优化以及插值两大过程。

图1 PIDW方法的流程Fig.1 The flowchart of the proposed PIDW method

1.1 各向异性表达模型

IDW插值模型如式(1)所示

(1)

式中，i代表任意待插值点；zj为点j处的实测值；Sij是未知点i与已知点j之间的距离；N为最邻近点数；α为距离衰减系数。

(2)

式中，(Xi,Yi)与(Xj,Yj)表示点i与j的笛卡儿坐标。

由式(2)可知，当λ等于1，那么Sij将等价于欧氏空间距离；当λ>1，如果两点之间ΔY越大，那么两点Y方向之间的距离将更远，即Y方向的空间邻近性减弱；反之，当λ<1，那么两点之间X方向的距离相对将增大，即两点的X方向的空间邻近性将减弱。如图2所示，距离调节参数λ能够改变最邻近点的选择，其中图2(a)为均质空间下所选择的空间邻近点，图2(b)为顾及各向异性时选择的空间邻近点。

图2 各向同性与各向异性环境下最邻近点的选择Fig.2 Illustration of the different selection of proximity points in the cases of isotropic and anisotropic assumptions

式(2)蕴含了数据的各向异性方向正好沿着数据的坐标轴，这与大多数的实际情况不符。因此，需要进一步引入方向参数θ来描述一般情形下的各向异性，从而可以建立原始坐标与反映各向异性坐标的转换关系，如式(3)所示

(3)

结合式(2)、式(3)，可以得到式(4)

(4)

式中，Eij表示待插值点i与样本点j之间顾及各向异性的距离；λ用于调节坐标系统下不同坐标轴的距离；θ∈(0,2π)表示原始坐标与各向异性坐标系的旋转角度；ΔX与ΔY为原始数据中待插值点与已知样本点之间的欧氏距离。

1.2 基于粒子群的多参数协同优化

考虑到影响IDW插值效果由距离衰减系数、最邻近点数、距离调节及方向参数共同决定，参数的确定本质上是一个多元变量的寻优过程。本文提出采用粒子群智能优化搜索算法[20]，通过CV方法构造粒子群优化的适应度函数，将多变量的优化问题转化为求解函数的极值问题，从而实现插值精度偏差与方差的总体满意效果。

1.2.1 粒子群算法

粒子群算法采用群体智能优化策略。首先，给空间中所有粒子分配初始随机位置和速度；然后，根据每个粒子的速度、问题空间中已知的全局最优位置和粒子已知的最优位置依次更新每个粒子的位置，通过种群内粒子间的合作与竞争机制来进行全局优化获得最优解。在D维空间中，设定粒子群数为Q，粒子i的位置表示为xi=(xi1,xi2,…,xiD)，粒子i的速度为vi=(vi1,vi2,…,viD)，pbesti=(pi1,pi2,…,piD)表示粒子i经历过的最佳位置，gbest=(g1,g2,…,gD)表示所有粒子的全局最佳位置，f(xi)为适应度函数[20]。其中粒子i的第d维位置和速度更新方法分别如式(5)、式(6)所示

(5)

(6)

1.2.2 适应度函数

粒子群算法的多参数优化问题关键在于确定适应度函数。为了降低可能的过拟合现象[21]，导致插值精度偏差与方差的背离，本文利用CV检验方法来构造PIDW算法的适应度函数，如式(7)、式(8)所示

(7)

xi=argminf(xi)

(8)

1.2.3 算法流程

1.2.3.1 确定4个参数(α,λ,θ,N)的组合解

(1)给定粒子群算法的初始化条件，搜索维度D=4(α,λ,θ,N)，α、λ、θ、N的搜索区间分别为[1，5]、[0.01，100]、[0，2π]及[4，30]，其中参数N和α的搜索范围是在参考文献[9—11]的基础上设定的，距离调节参数λ的范围根据经验确定，而角度参数θ的范围为所有可能的取值。采用随机初始化种群的方法产生一组包含(α,λ,θ,N)的解集合。

(2)计算粒子的适应度值。将每个粒子的xi代入式(7)的适应度函数，得到每个粒子的f(xi)。

(3)获取粒子i的个体最优值pbesti。对每个粒子，用其f(xi)值和个体最优位置Pbest(i)比较，如果f(xi)优于Pbest(i)，则用当前待优化参数的位置xi更新个体历史最佳位置Pbest(i)。

(4)获取群体的全局最优值。对每个粒子，将其当前f(xi)与全局最佳位置Gbest做比较，如果当前的适应值更佳，则用当前粒子的位置更新全局最佳位置Gbest。

(5)根据式(5)和式(6)对粒子的速度和位置(包括距离衰减系数、最邻近点数、距离调节参数以及各向异性方向)进行更新。

(6)如未满足粒子群算法的终止条件，则返回步骤(2)。本文设定迭代次数达到200或者最佳适应度值的增量比值少于1e-6时算法停止。

(7)输出最佳位置xi，即使得适应度函数值最佳时的距离衰减系数、最邻近点数、距离调节及各向异性方向参数。

1.2.3.2 插值

根据粒子群算法优化得到的参数组合解(α,λ,θ,N)，代入IDW插值模型(式(1))中获取待插值点属性值。式(1)中Si的计算方式采用本文顾及各向异性方向的“椭圆”距离计算方式Eij(式(4))，其中α、N、λ、θ分别为优化得到的距离衰减系数、最邻近点数、距离调节及各向异性方向参数。

2 试 验

本文使用不同分辨率的全国气温站点与黄河堤坝数据来验证PIDW算法的可行性，并将PIDW插值算法与经典的反距离平方加权(classical IDW,CIDW)、四象限IDW(four quadrant IDW,FIDW)[22]、自适应的反距离平方权重(adaptive IDW,AIDW)[23]、K近邻反距离平方加权(K-nearest neighbor adaptive IDW,KAIDW)[2]、普通克里金(ordinary Kriging，OK)以及顾及各向异性的克里金(anisotropic Kriging,AnisOK)进行对比试验。

(9)

(10)

(11)

2.1 年均气温插值试验

数据来源于中国气象中心2005年的682个气象站点的观测数据。通过前期的数据预处理，剔除少量观测台站仪器出现故障的数据，对每个台站的日平均气温求和，最终获取各个台站的年平均气温。由于气温与海拔存在约0.6℃/100 m的比例关系，本文根据气象站台的海拔数据，将每个气象站台的年平均气温归算到海平面。这样处理的理由是剔除不同高程对年均气温的影响，着重讨论经纬度变化对气温差异的影响[26](图3)。

图3 气象站点的分布Fig.3 Spatial distribution of national weather stations

为减少样本选择的影响，本文重复进行了3次随机抽样，其中每次从总体中抽取30个作为测试集，其余作为训练集。图3中“*”“·”及“+”形代表3次随机抽样的样点分布。经过PSO优化，PIDW的距离衰减系数α为1，最邻近点数N为7，距离调节参数λ为0.26，各向异性方向θ为0.02°。将计算结果的平均值作为插值精度的最终评价值。7种算法的对比结果如图4所示。

图4 利用MAE、RMSE及MAX指标评价7种算法的插值精度Fig.4 Comparisons the accuracies of seven different algorithms using MAE,RMSE and MAX measures

从图4(a)可以发现：CIDW与FIDW插值算法的MAE随着插值点数的增多呈现震荡式变化，并且FIDW的MAE显著低于CIDW；KAIDW、AIDW与FIDW的MAE大致保持一致，但OK和PIDW的MAE显著低于KAIDW、AIDW、FIDW和CIDW；OK的MAE低于PIDW，但最大偏差仅为0.007℃；AnisOK的MAE误差为0.52，低于PIDW的0.54。由图4(b)中可以看出：CIDW、FIDW和OK的RMSE随着点数的增多而下降，在参考点数量为13以上时趋于稳定；OK的RMSE稍好于AIDW与KAIDW方法，但劣于CIDW和FIDW算法；AnisOK的RMSE误差显著低于CIDW、FIDW、OK、AIDW、KAIDW；PIDW的RMSE为0.78℃，比次优的AnisOK方法低0.02℃。图4(c)中的MAX反映了与RMSE类似的规律：CIDW与FIDW插值算法随着点数的增多稳步下降，其中FIDW的MAX略低于CIDW，而AIDW与KAIDW的MAX表现最差；OK的MAX总体上优于AIDW和KAIDW，但明显差于CIDW和FIDW算法；PIDW的MAX显著低于CIDW、FIDW、AIDW、KAIDW以及OK；AnisOK的MAX具备一定的优势，相较于次优的PIDW方法，其最大值误差还要低0.4℃。

图4的结果表明：①顾及各向异的PIDW和AnisOK都显著优于CIDW、FIDW、OK、AIDW和KAIDW算法；②不存在哪种插值算法，其MAE、RMSE与MAX的3个指标上都占据一致性的优势；③顾及样点分布均匀性的FIDW插值算法精度普遍优于CIDW；④采用一阶邻近点作为参考样点的AIDW与KAIDW插值算法并未体现出较大的优势，可能是由测试数据集中一些位于边界区域的测试点所导致，顾及空间异质性的KAIDW未呈现比AIDW插值算法的优势，可能是由于KAIDW对于局部空间异质性的分类存在较多的误判；⑤OK相比于CIDW、FIDW、AIDW、KAIDW总体上并未呈现出明显优势，这可能是由于研究区域不能较好地满足OK插值算法所需的平稳性假设条件，导致变异函数未能较好地反映气温变化的变异规律；⑥PIDW插值算法除在MAE指标稍劣于OK插值算法，在其余指标上相较于未顾及各向异性影响插值算法具备明显的优势；⑦除RMSE指标外，AnisOK在MAE和MAX指标上低于PIDW插值算法。

2.2 DEM插值

DEM插值数据来源于黄河山东济南段大堤的1∶500大比例尺地形图，共采集了639个高程点。黄河大堤为“梯形”构造，其中此段大堤南北方向起伏大，而东西向高程则变化平缓，其中平均高程为43.03 m，最大高程为49.30 m，位于大堤的顶部，最低高程36.31 m。

试验中各算法的初始值与气温数据保持一致，PIDW算法得到最终的优化参数结果为[1.28，6，99，0]，各种算法的结果对比如图5所示。

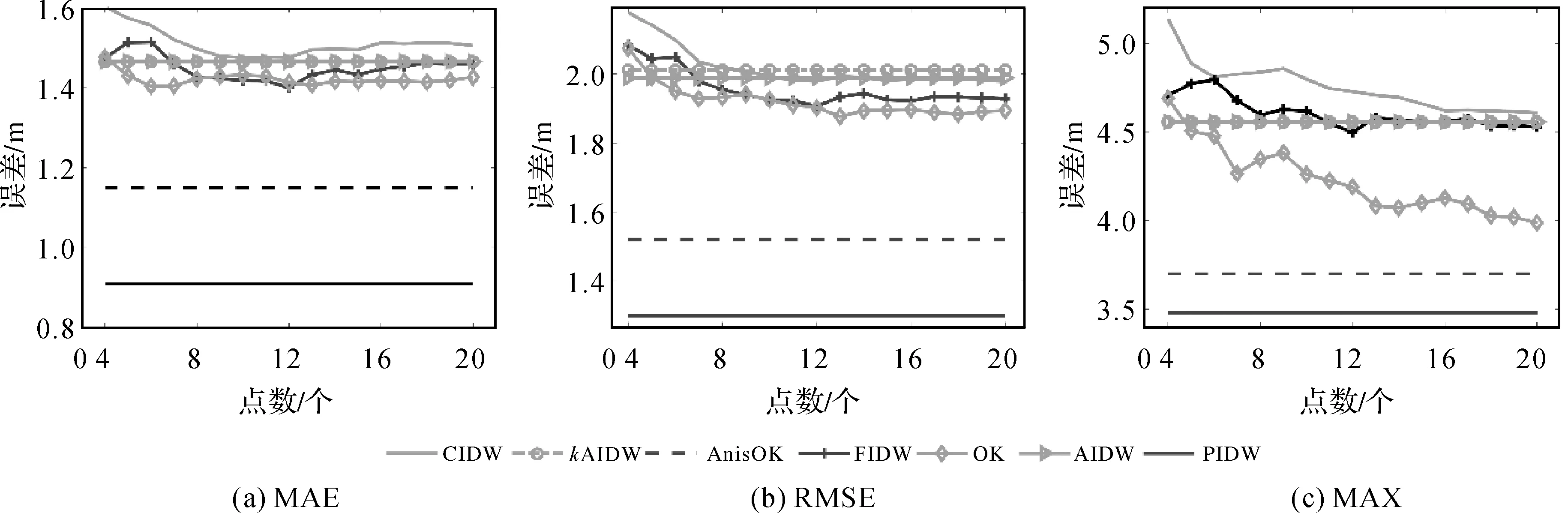
图5 对比7种算法在DEM数据插值的MAE、RMSE和MAX结果Fig.5 Comparisons of seven different algorithms in DEM interpolation with MAE, RMSE and MAX measures

从图5(a)中可以发现：随着插值点数的增多，CIDW、FIDW与OK的MAE逐渐下降，在采样点为12时达到最低，分别为1.43、1.37和1.42 m；AIDW与KAIDW的MAE低于CIDW算法，但大于其余3种算法；AnisOK的MAE误差明显低于CIDW、FIDW、OK、AIDW及KAIDW；PIDW表现出明显的优势，其MAE在7种插值算法中的误差最小，比次优AnisOK的最小MAE值再少27.3 cm。图5(b)中的RMSE表现出类似的结果：CIDW、FIDW和OK的RMSE随着点数的增多呈现下降，在样点为14以上时基本达到稳定状态，并且OK的RMSE值最小；AIDW与KAIDW的RMSE的结果最差；AnisOK的RMSE低于除PIDW外的5种插值方法；PIDW的RMSE指标在所有算法中同样呈现出明显的优势，比次优的AnisOK低27 cm左右。图5(c)表明CIDW、FIDW与OK的MAX随着点数增多而呈现下降趋势，在参考点达到17以上基本保持稳定；AIDW和KAIDW比CIDW与FIDW能够取得更优的效果，但PIDW的MAX显著优于其他插值方法。总结以上两个试验结果，可得出以下结论：①顾及各向异性的AnisOK与PIDW几乎在所有指标中都取得最小的误差，表明在计算过程中顾及各向异性的空间属性，将有助于提高模型的插值精度；②总体上PIDW的插值效果稍好于AnisOK方法，而且PIDW方法对数据无需假设前提，但地统计的AnisOK方法要求数据具有空间的二阶平稳性。

2.3 参数分析

为了解释PIDW插值算法有效性的原因，下面对模型的参数优化作进一步试验分析。

2.3.1 各向异性对空间邻近性的影响

由于各向异性能够引起空间邻近度的改变，因此设计对照试验来分析各向异性对空间邻近度的影响。图6(a)和图6(b)分别表示未顾及各向异性和顾及各向异性时对空间邻近度的影响。由图6(a)可知，当不顾及x或y方向的各向异性时，样本点与参考点之间的距离为同心圆模式，而当顾及各向异性的影响时，“同心圆”距离模式被压缩为“椭圆”，位于东西方向的样本点具有更强的空间邻近性。这表明PIDW的距离调节参数符合堤坝高程南北方向起伏大，而东西向变化平缓的事实。

图6 比较各向同性与各向异性环境下的空间邻近度Fig.6 Comparisons the spatial proximity between isotropic and anisotropic measures

2.3.2 各向异性的方向对空间邻近性的影响

考虑到各向异性的方向并不一定正好沿着坐标轴方向，而是存在一定的角度θ，本文设计一组对照试验来分析各向异性的方向对空间邻近性的影响。试验2的原始数据高程在南北方向变化速率比东西方向大得多。为了体现各向异性方向不沿x或y轴时对空间邻近性造成的影响，将试验2的数据逆时针旋转45°，即变换后的各向异性方向x_new与y_old之间的夹角约为135°(图7)。

由图7(a)可知，试验1得到的参考点与其余各样本点之间的距离基本为同心圆模式，不能真实地反映高程变化的空间邻近性，同时试验1得到的CV残差和为2 894.4也再一次证明了其拟合精度较差。试验2得到的CV残差为1 400.4，其计算得到的各向异性方向与原始y轴间的夹角为132.66°(图7(b))。可以发现，试验2的CV残差和较之于试验1低很多，同时试验2得到的各向异性方向与真实的方向相差仅为2.34°。同时由图7(b)可知，正确反映各向异性的方向能够得到准确的空间邻近关系。

图7 各向异性方向对空间邻近度度量的影响Fig.7 Illustrations of the anisotropic effects on spatial proximity measurement

2.3.3 多参数优化对比分析

影响PIDW插值精度的参数主要有各向异性(距离调节参数λ与各向异性方向参数θ)，距离衰减系数α和最邻近点数N。本文基于试验1的数据，设计如下5个试验来表明PIDW的插值精度由各参数共同决定，而单参数或少量参数的优化并不能取得插值的整体满意效果：①固定距离调节参数为1，方向值为0，优化最邻近点数与距离衰减系数；②固定距离衰减系数为2(ArcMap软件默认值)，优化最邻近点数、距离调节及各向异性方向参数；③固定最邻近点数为12(ArcMap软件默认值)，优化距离调节、各向异性方向参数及距离衰减系数；④固定方向值为0，同时优化距离衰减系数、最邻近点数及距离调节参数；⑤距离衰减系数、最邻近点数、距离调节与各向异性方向参数协同优化。试验采用MAE、RMSE和CV残差作为精度的评价指标，结果如图8所示。

图8 对比不同情形下参数优化的插值精度Fig.8 comparison the interpolating accuracies with optimized parameters for the different cases

从图8可以看出方案1的效果最差，其MAE、RMSE以及训练样本的CV残差值都最大。这是由于气温的分布存在较强的各向异性特征，如果插值过程中将距离调节参数固定为1，导致重要的参数不能正确地反映真实情况。方案2和方案3的MAE、RMSE和CV相较于方案1都有一定程度的提升，且方案3略优于方案2，表明本例中最邻近点数对影响插值精度的重要性要低于距离衰减系数。方案4的CV残差低于方案1、方案2和方案3，表明顾及各向异性影响能够得到较好的插值效果。从图8中还可以发现方案5的预测结果几乎与方案4完全一致，仅有CV的残差和相差0.1。这是由于气温变化沿着纬度方向变化速率较之于经度更快，而方案5优化的各向异性方向与方案4所固定的方向相同，因此其插值结果一致。由于粒子群算法的随机性，导致它们的CV残差和存在微小的差异。以上试验表明如果仅优化部分参数均难以获得插值效果的整体满意解，采取多参数整体优化方法将有效增强模型插值精度。由于PIDW算法也可能存在过拟合的现象，导致预测精度的降低，因而在实际应用中需要注意避免PIDW算法的过拟合问题。

3 结 论

本文提出了顾及各向异性的多参数协同优化IDW插值算法PIDW，通过引入描述距离调节的参数λ以及角度的参数θ，将传统的欧氏距离扩展为任意方向的“椭圆”距离，从而顾及各向异性对插值结果的影响；构造了基于CV检验的粒子群优化的适应度函数，将影响IDW插值精度的4个关键参数进行协同优化。利用不同尺度的空间数据验证了PIDW算法的插值效果，结果表明顾及各向异性的AnisOK及PIDW能够显著提高各向异性环境下插值算法的精度，PIDW几乎在所有指标中优于已有的IDW及OK插值方法。其次，PIDW总体插值效果稍好于AnisOK，并且不需要数据满足二阶平稳性假设条件，因此PIDW比AnisOK更具应用的普适性。

PIDW插值算法获得的协同优化参数是一种全局意义下的满意解。然而，当局部地理现象的变化特征与整体变化规律不一致时，那么PIDW算法得到的局部插值结果可能不如传统的IDW插值方法；其次，由于采用粒子群算法对影响IDW插值精度的多个参数同步优化，处理效率比传统IDW方法低。今后将在以下两个方面开展研究：①利用GPU加速或并行处理技术提升PIDW插值算法的效率[27]；②研究能识别局部各向异性特征的LPIDW插值算法。