基于机器学习方法的高速信道建模研究*
何 静,李晋文,杨安毅
(国防科技大学计算机学院,湖南 长沙 410073)
1 引言
随着人们对高速、高集成度的产品需求越来越大,高速有效地传输信号成为人们关注的焦点。眼图是评价高速电路设计质量的重要手段,人们通常使用眼图评估和分析高速信道设计。在寻找新的数值技术以提高生成眼图过程的计算效率方面进行了许多研究。
高速信道中传输的高速信号受到信道的非理想性影响而产生严重衰减和失真即码间干扰,使得接收端RX的眼图变小,为了消除码间干扰恢复理想信号,高速串行链路通常包含复杂的均衡摸块,本文釆用基于最小均方LMS(Least Mean Square)误差准则的最小均方算法来消除码间干扰,使眼图张得更大,提高均衡性能,优化该信道。
2 高速信道
近些年,随着云计算、大数据分析、物联网和人工智能的快速发展,人们对高速、高集成度的产品需求越来越大,高速有效地传输信号成为人们关注的焦点。数据传输的2大基本方式是并行数据传输和串行数据传输,因为并行信号虽然能够同时传输多路数据,但也需要更多的线缆及连接器,这就大大增加了通信成本和板级系统复杂度,并行信号传输过程的信号耦合与干扰也极大地限制了其传输距离和速度。现在传统并行数据接口的速度已经达到了瓶颈,它已无法满足高速传输数据信息的要求,进而速度更快的串行数据传输接口就取而代之了,SerDes(SerDes是英文Serializer(串行器)/Deserializer(解串器))技术成为了高速串行接口的主流。图1所示为SerDes串行通信技术示意图,即在发送端TX多路低速并行信号被转换成高速串行信号,经过高速信道传输媒体,最后在接收端RX高速串行信号重新转换成低速并行信号。SerDes可以实现远距离高速数据传输,这是使用宽并行总线也不可能实现的。

Figure 1 Sketch map of SerDes serial communication technology
SerDes技术的优点很多,因为它使传输带宽得到最大化利用,并且降低了传输信道与引脚数量等硬件开销,从而有效缩减了传输成本,也降低了PCB板级系统布线的复杂性。目前,SerDes在众多领域应用广泛,例如通信、电信、视频和工业等[1,2]。
随着通信速率的提高,传输信道的高频损耗、反射、串扰和码间干扰等对通信系统的限制也越来越严重,严重影响通信的可靠性。随着传输距离变长,传输速率变快,长线传输系统的接收端的数据得不到及时处理和反馈。为了补偿由于衰减、反射和串扰引起的信号衰减,并改善信道性能,设计人员通常采用均衡技术[1]。而LMS自适应均衡算法可以有效地加快数据处理速度,消除干扰,减小误码率,使传输距离延长,传输速率得到提高。所以,在长线传输中,接收端的均衡技术研究至关重要。现有的其他均衡算法过于复杂,计算速度慢,不能满足长线传输快速计算、实时信号处理的要求。所以,本文采用LMS自适应均衡算法。
3 学习方法
3.1 神经网络学习方法
3.1.1 DNN
机器学习本质上就是一种对问题真实模型的逼近。机器学习算法主要是指通过数学及统计方法求解最优化问题的步骤和过程。针对不同的数据和不同模型需求,选择和使用适当的机器学习算法可以更高效地解决一些实际问题。
作为最具民营经济活力的区县之一,常州市武进区在围绕解决当前民企发展过程中的矛盾,特别是在破解民企融资难题上,作出了一系列有益探索。
图2所示为神经元模型,输入信号为n个其他神经元传递过来的信号,触发神经元,这些输入信号相当于与带权重的连接组合,即为接收到总输入值,然后与神经元的阈值进行比较,再通过激活函数处理以产生神经元的输出,以此类推进行传递。将多个这样的神经元按一定的层次或者多层连接起来,就得到了神经网络[3]。
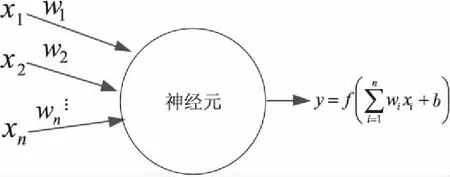
Figure 2 Neuron model
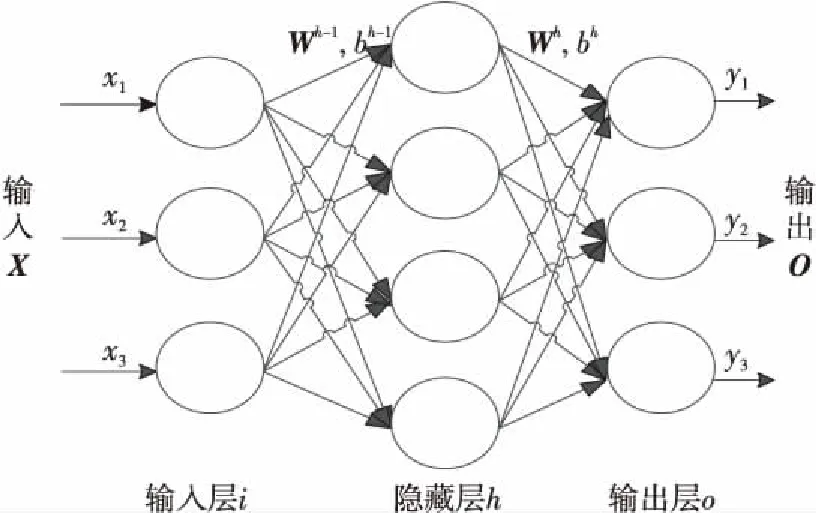
Figure 3 Neural networks
如图3所示,深度神经网络DNN由输入层、隐藏层和输出层组成。其中上标代表层,比如Xh-1代表第h-1层,也就是图中的输入层,X=[x1,x2,x3]T,下标代表具体神经元的值。结合图2和图3所示,神经元节点将第h-1层连接到第h层,W和b为权重和偏差,f为激活函数。
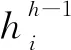
(1)
(2)
(3)
(4)
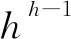
3.1.2 RNN
RNN循环神经网络又被称为时间递归神经网络。对于传统神经网络,前面的一个输入和后面的一个输入是完全没有关系的,但RNN中每一个时间步的隐藏层输入是由当前时间步的输入和上一时间步的隐藏层输出需要保留的信息共同决定。如图4所示,例如在t时刻隐藏层的输入由xt和上一时间步的隐藏层输出需要保留的信息st-1共同决定,因此历史数据的影响不会消失,而是会继续留存。每一时间步的RNN单元的具体结构如图4所示,每一个RNN单元都包括输入、隐藏层和输出。RNN单元的数量等于时间步数量,前一个RNN单元的隐藏层连接到下一个RNN单元的隐藏层,然后输出预测数据[4]。
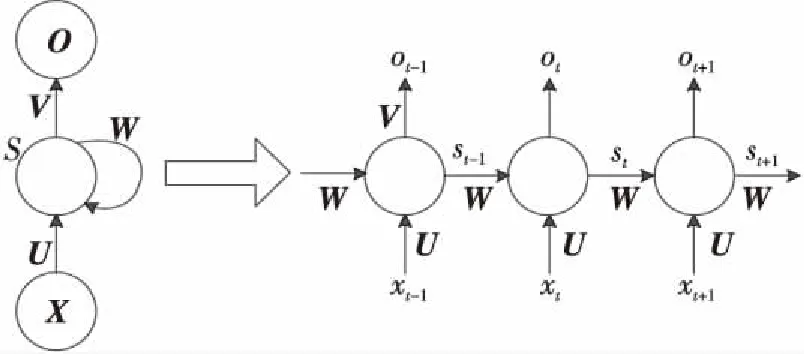
Figure 4 RNN
隐藏层:隐藏层节点数可以自己设定,暂定为m,隐藏层输入数据为:St=Xt·U+St-1·W。
输出层:输出层节点数为r,输出层的公式为:Ot=St·V。
其中,X为输入层数据的行向量,维度为1×n;W为连接相邻时间步隐藏层的权重矩阵,维度为m×m;U为连接输入层与隐藏层的权重矩阵,维度为n×m;V为连接隐藏层和输出层的权重矩阵,维度为m×r;S为隐藏层输入数据的行向量,维度为1×m;O为输出数据的行向量,维度为1×r。
RNN不像传统的深度神经网络,在不同的层使用不同的参数,循环神经网络在所有步骤中共享参数(U,V,W),即RNN在每一步都执行相同的任务,仅仅是输入不同。这个机制极大减少了需要学习的参数数量。此外,RNN每一步都是存在输出结果的,其可以根据用户需求进行调整,比如可以将每一步的输出作为输出结果,也可以将最后一步的输出作为最终的输出结果。
3.2 LMS自适应算法原理
LMS算法[1,5]所采用的规则是使均衡器的期望输出值和实际输出值之间的均方误差最小化的准则,即理想信号与滤波器输出之差的平方的期望值最小。
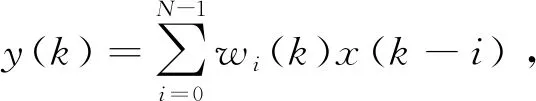
X(k)=[x(k),x(k-1),…,x(k-N+1)]T,则输出信号y(k)为:
(5)
误差序列e(k)=d(k)-y(k),其中d(k)是期望信号,按照均方误差准则所定义的目标函数是:
F(e2(k))=E[e2(k)]=E[d2(k)-2d(k)y(k)+y2(k)]
所以,按照自适应判决反馈均衡器系数矢量变化与矢量估计的方向之间的关系,可以给出如下公式:
w(k+1)=w(k)+u*e(k)*x(k)
(6)
其中,u为算法步长。
LMS算法的一个重要特点是将其期望值d(k)近似用瞬时值x(k)代替。算法步长u是设计自适应数字滤波器需要考虑的重要因素。在收敛的范围内,一般来说u越小,收敛速度越慢,但是滤波性能越高;u越大,收敛速度就越快,若u太大,收敛将变得不明显,过度过程将出现振荡,甚至造成计算溢出。
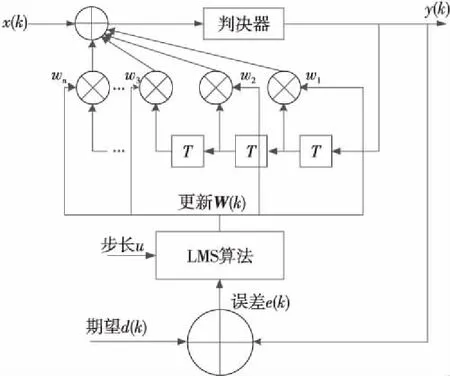
Figure 5 LMS algorithm for adaptive equalization
自适应均衡器的主要处理过程按照功能可以分为3部分:滤波、求误差和权值更新。在自适应状态下,首先自动调用调节滤波器系数的自适应训练步骤,然后利用滤波系数加权延迟线上各信号来产生输出信号,将输出信号与期望信号相比,所得的误差e(k)通过式(6)来调整权值,以保证滤波器处在最佳状态。
4 实验
4.1 采用神经网络仿真信道
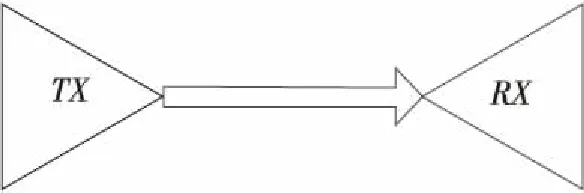
Figure 6 Data measurement settings
系统设置如图6所示[6],本文使用当前时间步的VTX来预测当前时间步的VRX。其中VTX代表信道前的输入信号,VRX代表通过信道之后的输出信号。
本文利用ADS(Advanced Design System)模型采集6 300个时间步长,开发环境是基于Anaconda,通过DNN算法,使用Python语言[7]实现。其中6 200个时间步长用来训练,100个时间步长用来预测。输入节点数是100,隐藏层节点数是50,输出节点数是100,训练次数400次,激活函数使用的是:
(7)
实验结果如图7所示,可以看出预测值与实际输出值几乎吻合。同样的数据用RNN神经网络,输入节点数是100,隐藏层节点数是50,输出节点数是100,训练次数仅100次,测试结果如图8所示。比较图7和图8可以看出,RNN明显优于DNN,结果更加准确。由于高速信道后续的输出与之前的输入相关,比较符合RNN的特性,所以对高速信道模型来说,RNN的效果优于DNN的。图9是预测输出眼图,输入电压是-0.5 V~0.5 V,由于信道损耗,输出值是-0.1 V~0.1V。
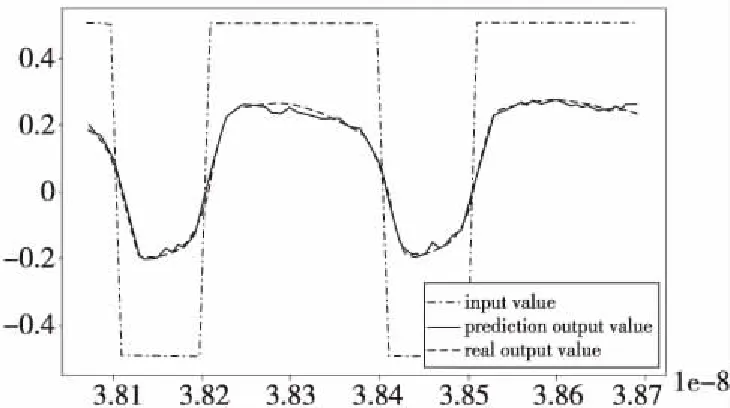
Figure 7 Prediction and real output values of DNN
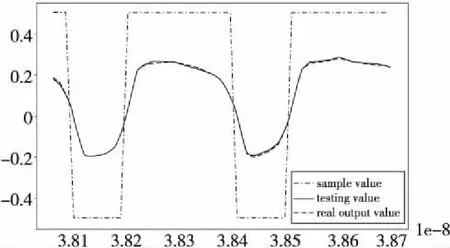
Figure 8 Prediction and real output values of RNN

Figure 9 Output eye diagram
4.2 采用LMS算法实现均衡
由于信道损耗引起信号失真,本文采用LMS自适应均衡算法实现,以提高均衡效果。同样采用Python语言实现。将RX输出信号作为LMS算法[8]的输入y(k),将标准TX信号作为LMS的期望值d(k),通过式(6)实现均衡算法,本文使用的u值为0.2。实验结果如图10所示,表明未经LMS均衡之前的幅值大概在-0.1 V~+0.1 V,经过LMS均衡后,眼图的幅值大概变为-0.4 V~ +0.4 V,效果改善明显。
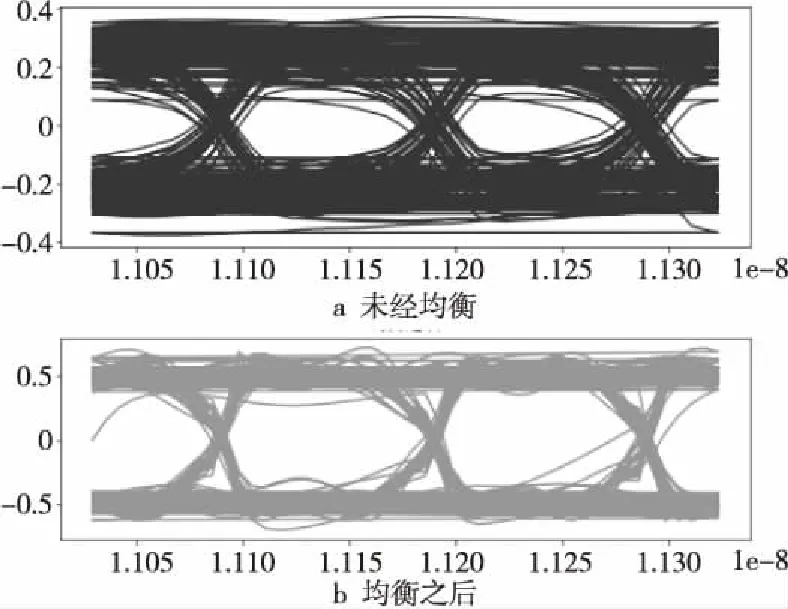
Figure 10 Eye diagram before LMS balance and after LMS balance
5 结束语
本文通过机器学习方法与高速信道技术结合,利用采集的大量模拟数据,提出采用深度神经网络 DNN 与循环神经网络 RNN 方法对信道建模,可以快速精准地对信号进行评估和分析,通过实验验证,效果良好。该方法不需要复杂的电路模拟,也不需要大量的领域知识。在现代计算机硬件上,模型训练可以很快完成,一旦训练结束,就可以高效地进行预测。
本文从功能上介绍了LMS均衡算法,然后对具体的算法进行了分析并用 Python 进行了实现,最后对该均衡算法进行了验证。从仿真对比的角度说明了该均衡算法的有效性。

