分布式环境中的多作业执行调度策略与优化*
季航旭,姜 苏,赵宇海,吴 刚,王国仁
(1.东北大学计算机科学与工程学院,辽宁 沈阳 110819;2.北京理工大学计算机学院,北京 100081)
1 引言
随着信息技术的快速发展,各个领域积累的数据量日渐增多。数据量的增加以及数据挖掘算法的研究与普及,使得人们越来越重视数据中隐含的价值,因此如何快速地从数据中获取有价值的信息成为各个研究领域的关注点。为了应对快速增长的数据,人们开发出了一代又一代大数据处理系统并产生了大量相关的优化技术。目前比较流行的大数据处理系统有Hadoop[1]、Storm[2]、Samza[3]、Spark[4,5]和Flink[6]等,它们都采用分布式集群的方式进行平台的搭建和系统的部署,并有着各自独特的优势。
目前,大数据计算系统已经普及,基于它们的数据查询和数据分析等任务也日益复杂化、多样化,如实时智能推荐、复杂事件处理等。分布式计算系统经常面临的挑战是资源分配与作业调度,这是分布式环境与生俱来的问题。由于分布式环境存在计算资源异构、带宽异构和单个作业内部计算方式复杂等情况,作业执行过程中经常出现由于资源分配不合理、调度优化不足导致的效率低、吞吐量低等缺点。更加令人堪忧的是,分布式计算具有计算结点规模大、计算任务复杂等特点,计算引擎往往要同时运行复杂繁多的分布式多作业,也就是所谓的分布式多作业。分布式多作业相比单作业在作业执行过程中将更加不利于计算资源的充分利用,这对于分布式大数据任务的执行将更加雪上加霜。目前,仍然没有一个完美的资源分配与管理机制满足分布式多作业的需求,因此资源的合理分配与回收仍然是提升大数据处理系统计算性能的关键。
现在最常用的大数据计算系统(如Flink、Spark)都是以多层执行图(Graph)的方式表示作业的具体信息与执行过程。多层执行图是计算系统在作业提交与作业执行之间生成的一系列有向无环图DAG(Directed Acyclic Graph),也是计算引擎中最核心的数据结构,它们决定了分布式作业在每个节点上的资源部署。也就是说,分布式任务的执行都是根据执行图中的信息在每个节点上进行任务部署。因此,如何在多作业执行过程中使DAG的合并达到最优,以及如何优化作业的提交顺序与调度策略,将是高效执行多作业的重要保障。
本文通过对主流的大数据处理系统的研究和探索,结合目前流行的大数据处理系统优化技术,提出并实现了在作业层面上的多作业合并算法与调度策略。本文的主要贡献点在于:
(1)提出了一种启发式作业合并算法。通过采集到的作业特征,以作业并行度为基础分析DAG结构上的差异性,合并浪费资源的作业,释放占用资源较少的作业资源,提高集群资源的利用率。
(2)提出了一种基于负载均衡的多作业调度算法。根据基于作业特征的多路K-means聚类算法的分析结果使用基于负载均衡的多作业自平衡轮询调度算法提交作业,进一步达到系统负载均衡。
(3)使用目前最新一代大数据计算系统Flink对本文提出的作业合并算法与多作业调度算法的有效性进行了验证。结果表明,2种作业合并算法都可以减少作业的运行时间,提高系统吞吐量;基于负载均衡的多作业调度算法在最好情况下可减少40%的线程启动数。
2 相关工作
2.1 DAG计算模型
DAG是分布式计算领域中很常见的一种数据结构,通常由一系列用户自定义的算子组成,在各种大数据处理系统中都能发现它的身影,比如Storm、Spark和Flink等。DAG计算将计算任务分解成为若干个子任务[7],并将这些子任务之间的逻辑关系或顺序构建成DAG结构。大数据计算引擎中的DAG计算通常可以抽象为3层结构:应用表达层、执行引擎层和物理执行层。应用表达层位于最上层,定义相关算子和转换,将计算任务分解成由若干子任务形成的DAG结构,其优点是表达的便捷性,便于开发者快速描述或构建大数据应用。执行引擎层介于应用表达层和物理执行层之间,将应用表达层构建的DAG计划任务通过转换和映射,部署到下层的物理机集群中运行,任务的调度[8]、底层的容错恢复机制、数据与集群信息的传递等都要依赖执行引擎层。下层是物理执行层,即物理集群。
2.2 Flink中的DAG
Flink是Apache 开发的一个同时用于处理批数据和流数据的有状态的计算框架和分布式处理引擎。Flink使用4层DAG结构来描述和表达作业的执行流程,每一层都对作业执行流程做了不同程度的封装、优化和相关属性的配置。DAG结构是Flink作业执行和部署的核心,主要包含数据流图(StreamGraph)、作业图(JobGraph)、执行图(ExecutionGraph)和物理执行图,Flink正是通过这4层图结构把整个作业的优化、资源分配和算子部署进行分离。Flink的4层DAG结构如图1所示。
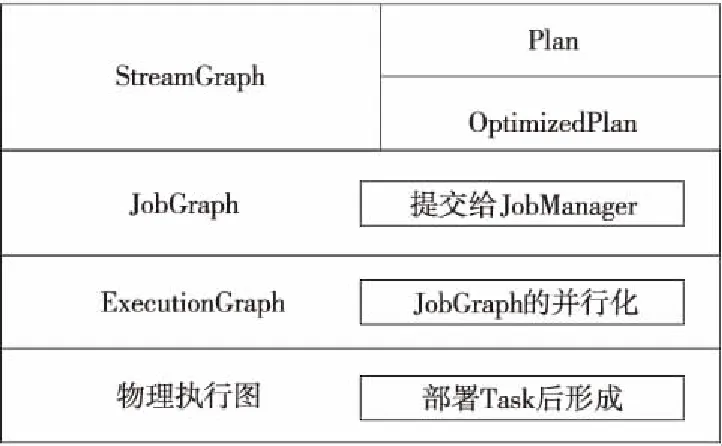
Figure 1 Four-layer DAG structure of Flink
图1中,数据流图是用户通过API接口编写的、用来表达用户所要执行的计划任务的逻辑结构。作业图是在数据流图的基础上进行优化以及调整各种参数配置后的数据结构,它裹挟着作业运行期间所需的必要信息。这些信息被客户端提交到集群中的协调中心,即作业管理器(JobManager)。执行图可以被视作并行化的作业图,当接收到一个新的作业图时,会把其中的每一个算子按照其并行度转化成多个可实际部署的子任务(在执行图中以Execution表示)。当执行图中的一系列子任务真正在从结点机器上运行的时候,才会构成物理执行图。
2.3 多作业执行与调度研究现状
目前最流行的大数据处理平台默认情况下都以FIFO的形式调度作业。Wang等[9]为了解决在虚拟化云环境中同时运行的多个作业之间的干扰问题,开发了数据驱动分析模型,估计多个作业之间的干扰对作业执行时间的影响,并为此提出了一种干扰感知作业调度算法。黄廷辉等[10]通过对分布式系统关键技术的分析,得出I/O和CPU的不匹配是影响计算性能的一个重要因素,提出合并文件的运行方式,可以减少缓存文件的数量,提高I/O效率,不过仍存在内存成本高的弊端。
Flink系统中资源是按处理槽(Slot)进行划分的,支持多种已有的成熟的资源管理器,例如Yarn和Mesos等。Storm作为曾经最流行的流式大数据处理系统,默认是采用轮询的调度方式管理作业的[11]。Qian等[12]为了解决Storm集群中扩展更多新计算机时带来的负载不均衡问题,设计了S-Storm,为负载均衡群集中均匀分配Slot。总之,目前的分布式作业调度算法和资源分配算法都是基于作业对资源的需求或者集群中结点资源的使用情况,进行作业的调度和资源的分配的,它们面向的是单个作业,并没有考虑作业间的关系对集群性能的影响。
3 基本概念
一个复杂的DAG通常由多种类型的算子组成,有些算子只涉及本地运算,它们以内存共享的方式传输数据,运行效率高,给系统增加的负载小。也有些算子会通过网络协议栈传输数据,除了网络本身的不可靠性会增加延迟,还有网络缓冲数据、序列化、反序列化和用户态/内核态之间的切换等耗时操作持续地占用系统资源。为了便于描述,本文定义了全局算子和本地算子这2个概念。
定义1(全局算子) 全局算子指在分布式集群中,需要从其他结点获取数据进行处理的算子,如Join和Reduce等。
定义2(本地算子) 本地算子指在分布式集群环境中,不需要从其他结点获取数据,只对本地数据进行处理的算子,如Filter、Map和FlatMap等。
本文在研究作业合并和作业调度时需要提取DAG的相关特征量,计算作业之间的差异性并通过聚类算法对作业进行区分。聚类算法是一种经典的群分析方法[13],它以数据间距度量数据相似性[14],把相似的数据集中到一起,是一种发现数据集内部结构特征的无监督学习算法[15]。聚类算法按聚类思想可以分为:划分法聚类、密度法聚类[16]、图论聚类法[17]和网格法聚类等。
本文采用的K-means算法是一种典型的划分聚类法,其思想是预先指定聚类数目和聚类中心,计算点与点之间的距离,把每一个点归类到与其距离最近的聚类中心。距离的度量方式很多,本文使用欧氏距离(式(1))和曼哈顿距离(式(2))相结合的方式度量作业之间的距离,其中n为样本点维度。
(1)
(2)
欧氏距离从几何空间的角度衡量元素间的距离,常用于测量度量标准一样的数据间的距离;曼哈顿距离用来计算数据在多维属性上的差之和,可以减弱离群数据带来的影响。
4 基于启发的作业合并算法
本节详细介绍基于启发的作业合并算法。首先对作业进行分析,解析作业的DAG图,以及作业任务量与作业分配到的内存资源之间的关系;然后分别采用基于并行度的作业合并算法和基于DAG结构差异性的作业合并算法,对占用系统内存资源较多的作业进行合并,从而提高系统的吞吐量。
4.1 作业相关特征的提取
本文采用广度优先遍历的方式提取作业执行图中相关的信息,一个典型的作业执行图如图2所示,主要包含以下信息:数据源文件路径、作业并行度和算子总数等。

Figure 2 Job execution graph
处理的数据量和作业分配到的内存资源需要通过计算获得。算法根据文件路径信息访问文件大小,从系统配置文件中读取为Slot分配的内存大小。作业的分类贯穿于信息采集过程,算法根据数据来源、文件大小、作业分配到的内存资源大小和作业的执行逻辑将作业分为可合并型作业与不可合并型作业。在作业执行流的遍历过程中,算法以矩阵结构存储顶点间的连接信息,元素值的大小表示算子间的连接数。表1是对图2的信息提取。

Table 1 Statistics of the number of connections between operators
4.2 基于并行度的作业合并算法
并行度决定了作业在执行时所占集群内存资源的总量,且和集群中的Slot是对应的,意味着并行度相同的作业将分配到相同大小的内存资源。因此,对于没有充分占用内存资源的作业,合并并行度相同的作业,可使2个作业共用1个作业的内存资源,同时不会对作业执行逻辑造成影响。
影响作业执行的因素有很多,定义3~定义5的3个度量:任务量大小比值(F)、DAG最大深度比值(D)和DAG全局算子数比值(G),决定作业的特征。
定义3(任务量大小比值(F)) 任务量大小比值是表示2个作业处理任务量大小差异性的重要指标之一,其计算如式(3)所示:
(3)
其中,x和y分别表示2个作业所处理的数据集数量,wf_mi、wf_mj分别表示2个不同作业处理的文件集合中单个文件的大小。通过实验得知,F的阈值取值为[0.5,2]。
定义4(DAG最大深度比值(D)) 表示2个作业的执行图中最长算子链长度的比值,它是反映2个作业DAG差异性最明显的指标,其计算如式(4)所示:
(4)
其中,dept_m和dept_n分别表示2个作业执行图的最大深度。DAG深度越大的作业执行时间越长,因此合并后的作业在数据量相当的情况下,其执行时间取决于合并前DAG深度较大的作业。D的阈值取值为[0.5,2]。
定义5(DAG全局算子数比值(G)) 表示2个作业图在全局算子数量上的差异。全局算子和数据传输紧密相关,是影响作业执行速度的重要指标之一,体现2个作业在传输上的差异。其计算如式(5)所示:
(5)
其中,G表示2个并行度相同的作业的全局算子数的比值,gol_m和gol_n分别表示2个作业中全局算子的个数。DAG中全局算子的个数越多,执行时间越长。通过实验得知,G的阈值取值为[0.5,2]。
基于并行度的作业合并算法执行过程如算法1所示。
算法1基于并行度的作业合并算法
输入:待合并作业j;不包含j的待合并作业集合Jobs。
输出:合并后的作业mergeJob。
1.forjobinJobsdo
2.ifjob.parallelism==j.parallelism
3.计算j与job任务量比值F;
4.ifF∈[0.5,2]do
5. 计算j与job的DAG图最大深度比值D;
6.ifD∈[0.5,2]do
7. 计算j与job的全局算子的比值G;
8.endif
9.ifG∈[0.5,2]do
10.mergeJob=merge(j,job);
11.removejobfromJobs,returnmergeJob;
12.endif
13.endif
14.endif
15.endfor
(1)首先从待合并作业缓冲池的作业集中取出一个作业j,然后遍历Jobs,从中取出一个与j并行度相同的作业job。
(2)使用3个度量值衡量作业job与j的匹配程度,如果job与j在上述3个比值上都能落到对应的阈值空间,两者匹配,调用merge函数合并job与j,返回合并后的结果,终止循环;否则继续循环。
(3)循环结束后,检查mergeJob的值是否为空,如果mergeJob的值为空,说明Jobs中没有与j并行度相同并且符合3个条件的job,那么j会转而参与基于DAG图结构差异性的作业合并计算。
4.3 基于DAG结构差异性的作业合并算法
对于作业缓冲池中剩余的由于F、D、G取值落在阈值空间以外而无法合并的作业,采用基于DAG结构差异性的作业合并算法处理。
算法以DAG结构差异性为切入点,Slot只隔离内存资源,因此为了避免作业对CPU资源的争抢,尽量选择异构程度高的作业进行合并。算法增加2个度量为基于DAG结构差异性的作业合并算法提供支持。
定义6(作业并行度比值(P)) 作业并行度是作业最明显的特征之一,并行度比值是衡量2个作业在并行度上的差异最明显的指标。其计算如式(6)所示:
(6)
其中,P表示2个作业并行度的比值,parallelism_m和parallelism_n表示2个作业的并行度。并行度是对应于集群中的Slot数量,因此基于DAG的作业合并算法在合并作业时首先需要考虑的就是作业并行度。通过实验得知,P的阈值取值为[0.5,2]。
定义7(DAG结构相似性(S)) DAG结构相似性反映2个作业在执行逻辑上的差异,以欧氏距离为基础定义了DAG结构相似性,其计算如式(7)所示:
(7)
其中,o表示算子的数量。
在特征提取过程中使用矩阵保存作业执行流程图的基本信息,M和N分别表示存储作业执行流程图基本信息的矩阵,Mij和Nij分别表示矩阵中的元素。算法执行过程如算法2所示。
算法2基于DAG结构差异性的作业合并算法
输入:待合并作业j;不包含j的待合并作业集合Jobs。
输出:合并后的作业mergeJob。
1.按并行度大小给Jobs中的作业从小到大排序
2.中间作业集合为midJobs;
3.forjobinJobsdo
4. 计算j与job任务量比值F;
5.ifF∈[0.5,2]do
6. 计算j与job的DAG图最大深度比值D
7.ifD∈[0.5,2]do
8. 计算j与job的全局算子的比值G
9.ifG∈[0.5,2]do
10. 计算j与job并行度比值P
11.ifP∈[0.5,2]do
12. addjobtomidJobs
13.endif
14.endif
15.endif
16.endif
17.endfor
18.forjobinmidJobs
19.计算j与jobDAG图矩阵间的欧氏距离U;
20.更新U获取最小值,并记录相应的job;
21.endfor
22.mergeJob=merge(j,job)
23.returnmergeJob
(1)从待合并作业中取出一个作业j,然后遍历Jobs,获取一个与j并行度相同的作业job;
(2)在循环中使用4个度量值衡量作业job与作业j的匹配程度,如果符合对应的阈值空间,则把作业job加入到中间作业集midJobs中;
(3)遍历中间作业集合midJobs,使用欧氏距离从中间数据集合中选出与作业j在欧氏距离上相似度最小的作业job,合并作业j与job并返回结果。
5 基于负载均衡的多作业调度算法
除了作业合并之外,作业的执行顺序与调度策略也是影响多作业执行效率的重要因素。因此,本文提出基于负载均衡的多作业调度算法,其由3部分组成:
(1)预处理模块:进行相关特征的提取工作,包括作业并行度、算子个数和算子类型等;(2)分类模块:采用K-means聚类算法根据提取的特征信息对作业进行聚类分析,聚类算法在负载均衡方面应用广泛[18,19],经过聚类把作业分成3个类别:大作业、中等作业和小作业;(3)调度模块:调度模块根据聚类结果,使用自平衡轮询调度算法计算作业的提交顺序,同时充分利用集群的Slot资源,防止Slot闲置。
5.1 作业相关特征的提取
基于负载均衡的多作业调度算法主要使用作业并行度、算子总数、各类型算子个数和作业图深度为参考,通过遍历对信息进行采集。该算法执行过程如算法3所示。
算法3DAG特征提取算法
输入:作业DAG结构图Plan。
输出:提取到的信息集合infoList。
1.fornodeinPlando
2.max=Math.max(max,BFS(node));
3.ifnodeis not visited
4. add node’s characters toinfoList,node.visited=true;
5.node相连接的未被访问的顶点入队列Q;
6.whileQis not emptydo
7.v=Q头元素出队列;
8.addv’s characters toinfoList,v.visited= true;
9.v相连接的未被访问的顶点入队列Q;
10.endwhile
11.endif
12.infoList.max=max
13.endfor
14.returninfoList
(1)使用深度优先搜索DFS(Depth First Search)计算从Sink算子到距离最远的Source算子的距离,并记录在max中;如果node顶点未被访问过,将顶点信息存入infoList中。
(2)将与node顶点相连的顶点加入队列Q,如果Q不为空,从Q中取出一个顶点v,将v的信息记录到infoList中,与v相连的未访问过的顶点加入队列。
(3)更新infoList中的DAG深度,for循环直到遍历完Plan中的所有顶点,返回infoList。
5.2 基于作业特征的多路聚类分析
聚类分析模块将根据特征信息对作业进行分类,使用4种数据度量作业之间的相似性,分别是作业并行度、各类算子个数、作业执行流程图深度和全局算子的个数。算法采用欧氏距离与曼哈顿距离相结合的方式测量作业间的距离。ope[i]是以数组的形式存储,dept、全局算子ops的大小是衡量作业流程复杂性的度量标准。
定义8(作业在不同算子类型上的差异性) 算子及算子类型最能区分作业的不同,算子类型的差异性反映了作业的总体差异性,其计算如式(8)所示:
(8)
其中,mope[i]与nope[i]分别为作业m与作业n的不同类型的算子的个数。
定义9(作业在DAG结构深度上的差异性) DAG结构深度是作业最明显的特征之一,它描述了作业运行时数据流通的最大路径,其计算如式(9)所示:
distancedept(m,n)=|mdept-ndept|
(9)
其中,mdept与ndept分别为作业m与作业n的DAG结构深度。
定义10(作业在Task线程数上的差异性) 作业在集群中开启的线程数直接反映作业对系统CPU资源的占用量,作业在Task线程数上的差异性计算如式(10)所示:
distancetasknum(m,n)=|mpara*mops-npara*nops|
(10)
其中,mpara与npara分别为作业m与作业n的并行度,mops与nops分别为作业m与作业n的全局算子数量。
定义11(作业的差异性) 本文从3个角度衡量了作业之间的差异性,其计算如式(11)所示:
distance(m,n)=distanceope(m,n)+distancedept(m,n)+distancetasknum(m,n)
(11)
本文提出的基于作业特征的多路K-means聚类分析算法如算法4所示。
算法4基于作业特征的多路K-means聚类分析算法
输入:作业及其特征集合PlanList。
输出:聚类结果ClusterResult。
1. 根据并行度乘以算子总数的大小对PlanList进行排序;
2. 获取初始聚类中心点集合;
3.fori=1 to 3do
4.center_i=K_means(PlanList,center_i);
5.endfor
6.fori=1 to 3do
7. 计算每个聚类中心点将PlanList划分的程度;
8.endfor
9.center=K_means(PlanList,center);
10.根据center将PlanList分组并放入ClusterResult中
11.returnClusterResult
(1)对作业及其特征集合PlanList按并行度乘以算子总数大小进行排序。
(2)从排好序的PlanList中选择3个作业作为聚类中心;以排好序的PlanList的队列头作业、队列尾作业和中间作业作为聚类中心;从排好序的PlanLsit中分别取队列头3个作业、队列中间3个作业、队列尾部3个作业,取其平均值作为聚类中心。
(3)调用K_means算法循环更新每个聚类中心的值;计算每个聚类中心将PlanList划分的程度,划分程度度量标准为,聚类结果每类作业的数量越平均越好。选取聚类结果好的2个聚类中心取其平均值,调用K_means算法进行最后聚类;计算聚类结果,并输出结果。
5.3 基于负载均衡的多作业自平衡轮询调度
通过多路聚类的方式优化了聚类中心点的选取,通过基于作业特征的多路K-means聚类分析可以把作业集合根据聚类中心点聚集成3个作业类别,为算法提供可靠的支持。
本文以轮询调度法[20 - 23]为基础实现了多作业的提交优化,目的是在不浪费集群Slot资源的情况下,使集群开启的Task线程数量保持平稳,以此达到在多作业情况下平衡集群性能的目的。集群中作业工作的线程数量是由作业并行度和算子个数决定的,因此控制作业的提交顺序,可以达到控制集群开启的Task线程数量的目的。作业能否提交成功取决于集群剩余并行度是否满足作业的并行度需求,如果作业的并行度比集群中可用并行度大,作业就会被拒绝,因此轮询的作业提交方式并不会严格执行,而且集群空闲的Slot资源会随着作业的提交和结束动态地变化。针对这种情况本文设计了自平衡的轮询调度算法,如算法5所示。
算法5基于负载均衡的多作业自平衡轮询调度算法
输入:聚类结果ClusterResult;最后的聚类中心center。
输出:下一个提交的作业Job。
1. 对K-means聚类结果收集排序;
2. 平分排好序的作业到3个队列中,并设置指针p;
3.翻转队列midQueue、minQueue,查询集群剩余Slot;
4.ifslotNum> 0do
5.ifjobNum> 0do
6.pre=p;queue=Queue[p];
7.whilequeueis not emptydo
8.max= 0;
9.foreleminqueuedo
10.ifelem.parallelism≤slotNumdo
11.ifmax 12.job=elem;max=elem.parallelism; 13.endif 14.endif 15.endfor 16.endwhile 17.ifmax!= 0do 18.p=(p++)%3; 19.endif 20.ifmax== 0do 21.p=(p++)%3; 22.ifp==predo返回 4; 23.endif 24. 返回 7; 25.endif 26.endif 27.endif (1)对K-means聚类产生的3个集合中的元素按元素距离聚类中心点的距离大小进行排序;比较3个聚类中心点的大小,按聚类中心点的大小,从大到小合并3个排好序的作业集合。 (2)将合并后的集合平均分成3份,并放入3个队列中,将midQueue和minQueue队列进行逆转。 (3)每隔5 s查询一次集群剩余Slot资源,从指针指向的队列开始,遍历队列中的元素找到集群中空闲Slot资源能满足的最大并行度的作业提交。每次提交作业后,修改指针指向下一队列。 (4)对3个集合进行判断,如果出现队列为空,并且总作业的数量大于2,按顺序收集3个集合中的队列,再平分所有的作业到3个集合中,并更改指针使其指向midQueue,否则不再进行作业收集。 本文使用2种类型的作业来进行对比实验,一种是单词统计(WordCount),另一种是表连接(Join)。因为全局算子中最复杂的算子就是Join类型算子,其他简单类型的算子使用最多的是Filter、Map和FlatMap,因此WordCount作业和Join作业足以覆盖实际应用中的大部分场景。 本文实验采用大数据测试基准TPC-H生成的数据集,是事务性能管理委员会TPC(Transaction Processing Performance Council)发布的权威数据库评测基准,可以保证生成的模拟数据具有真实性、客观性与健壮性。在WordCount实验中本文选用5个基本的大数据集来模拟批处理环境中的大规模数据处理。在表连接实验中,本文选取TPC-H生成的Lineitem表和Orders表作为数据源,其中Lineitem有16个字段,前3个字段Orderkey、Partkey和Suppkey是主键。Orders表有9个字段,前2个字段Orderkey和Custkey是主键。 实验的评估指标有3个: (1)作业运行时间:在相同硬件条件下,任务量相同、处理逻辑相同的作业处理速度越快,表明系统性能越好。 (2)作业吞吐量:单位时间内集群处理的平均数据量大小,即被处理的总数量(totalDataVolume)与运行总时间(totalProcessTime)的比值,其定义如式(12)所示: (12) (3)集群开启的最高Task线程数:本文提出的基于负载均衡的多作业调度算法以降低集群同一时刻开启的最高Task线程数为首要目标。 本文所描述的相关技术细节均在Flink 1.8.0版本中进行实现,实验运行的软硬件环境如下所示: (1)硬件环境:采用的分布式环境由4台服务器组成,1台主结点,3台从结点,结点之间通过千兆以太网连接。配置为:CPU:Intel Xeon E5-2603 V4 *2,核心数目:6核心;内存:128 GB(从结点64 GB);硬盘:400 GB SSD。 (2)软件环境:操作系统:CentOs 7;Flink版本:1.8.0,JDK版本:1.8.0;存储环境:Hadoop 2.7.5。 (1)基于并行度的作业合并算法实验。 作业合并算法实验对一对相同的WordCount作业和一对不同的Join作业分别进行顺序执行和合并执行。表2展示了作业的基本信息。 Table 2 Job sets information for experiment 1 图3对比了2个WordCount作业在相同实验环境、相同数据集上顺序执行和合并执行的执行结果。其中图3a对比了执行时间,合并执行的执行时间减少了5%~23%。在内存资源足够使用的前提下,单个WordCount程序对集群CPU的利用没有达到时刻满负荷运行的状态,所以作业合并不仅能提高集群的内存资源利用,也能提升集群CPU资源的利用。图3b对比了吞吐量,采用了作业合并算法后系统可以更快地到达吞吐量峰值。 Figure 3 Results of WordCount job merging based on the number of parallelism 图4对比了Join1和Join2作业在相同实验环境、相同数据集上顺序执行和合并执行的执行结果。其中图4a对比了运行时间,图4b对比了系统吞吐量。尽管效果不如WordCount作业明显,但基于并行度的作业合并算法对运行时间仍有一定缩减,吞吐量提升效果在4.5%~20%。 Figure 4 Results of Join job merging based on the number of parallelism (2)基于DAG结构差异的作业合并算法实验。 实验先后提交了2个并行度不同的WordCount作业和Join作业,来模拟基于DAG结构差异性的作业合并。 图5和图6从运行时间和吞吐量2个方面展示了作业合并算法的提升效果。合并执行的执行时间明显低于顺序执行的总时间,并且差距明显,因为本实验不是在满并行度的条件下进行的,实际执行时可能会出现不同情况,对于WordCount作业,基于DAG结构差异性的作业合并算法具有明显的优势。 Figure 5 Results of WordCount job merging based on DAG structure difference Figure 6 Results of Join job merging based on DAG structure difference (3)基于负载均衡的多作业调度算法实验 对于多作业调度算法,实验以4个作业为基础,表3列出了作业算子的基本信息,这些作业特征信息是衡量作业之间差异性的关键。实验模拟了7个任务量大小不同的作业,采用随机的方式模拟了作业的提交顺序,将其执行结果与多作业调度算法的结果进行比较。表4展示了作业对应的编号以及其处理任务量信息,表5展示了优化前后作业的提交顺序。 Table 3 Job sets information for experiment 3 Table 4 Job number and corresponding processing task volume Table 5 Order of job submission 图7展示了基于负载均衡的多作业调度算法的提升效果。从图7a可以看出,通过调优作业的提交顺序可缩短作业处理的时间,但存在某些按FIFO提交模式的顺序比优化后的轮询提交顺序要好,该情况的出现是因为算法在执行过程中并未考虑到任务量的大小。从图7b可以看出,基于负载均衡的多作业调度算法在吞吐量性能上提升了5%左右。图7c 展示了集群开启的Task线程数对比,基于负载均衡的多作业调度算法执行作业集时,集群开启的最大线程数在多数情况下有所减少,最好情况下减少了40%的线程。 Figure 7 Running results of multi-job scheduling algorithm based on load balancing 本文通过分析作业与系统资源之间的关系,以及作业与作业之间的关系,提出并实现了提高集群资源利用率和负载均衡能力的算法,本文提出的优化主要包含2个方面: (1)提出了启发式的作业合并算法,通过分析作业任务量和作业分配到的集群资源之间的关系,合并对集群资源利用率低的作业,使它们共用同一个作业的资源。该算法解决了集群部分作业资源利用率低的问题,并通过实验验证了该算法在不同类型作业上对集群性能提升的有效性。 (2)提出了基于负载均衡的多作业调度算法,首先对作业进行特征提取;然后通过多路K-means聚类算法将作业分为3类:大作业、中等作业和小作业;之后采用自平衡轮询调度算法提交分类好的作业,保证大作业不会在集群中集中执行,降低了集群由于开启过多线程造成集群性能下降的概率,并通过实验验证了该算法的有效性。 分布式系统在多作业执行层面还有许多需要优化和提高的部分,未来可继续研究的问题有: (1)动态调度。目前的分布式大数据处理系统未能做到在作业执行过程中动态地调整作业的执行流程,这种方式不利于资源的动态回收与共享。针对这一问题,系统需要做出相应的优化和改进。 (2)优化多作业并行度。并行度是作业执行的关键,目前在分布式大数据处理平台的应用中,一般都是从业人员根据数据与业务特性手动优化并行度,这样就给并行度的优化带来了很多困难。因此,研究和设计出一套并行度设置的优化方案,也是分布式大数据系统应用方面的一个研究课题。6 实验
6.1 数据集与评估指标
6.2 实验环境设置
6.3 实验结果与分析









7 结束语

