货架管理模型的选品与布局启示＊——以自动售货机为例

■ 毛宇晨 黎俊

中国科学院大学经济与管理学院 北京 100190

0 引言

随着中国在线支付技术的发展，货架管理问题已成为零售企业面临的热点问题。具体而言，出于日益增加的商品种类数量与有限货架空间之间的矛盾：一方面，可供销售的商品种类日益增多，不同商品其规格与需求不同；另一方面，尽管零售企业已改良自动售货机内部结构以扩大商品摆放数量，但是仍存在自动售货机空间大小的限制。因此，如何科学地决策自动售货机的商品种类以及设计货架商品布局以提高零售企业收益尤为关键。

作为供应链管理领域的一个重要问题，本研究首先回顾与本研究关系最为密切的货架管理相关研究。Baron 等[1]分析了多商品的联合货架布局与库存决策问题，其中商品需求受货架布局以及库存水平影响；Urban等[2]分别研究了选品与货架布局模型，并将其拓展到多产品、多约束的情形；Hübner等[3]首次提出同时决策选品与货架布局的货架管理模型，其考虑了需求的随机性与空间弹性、以及替代商品的影响；Geismar 等[4]考虑了二维矩形空间分配问题，其中产品需求由其排列位置决定；Hübner等[5]进一步总结了二维货架管理模型的建模与求解方法；更多相关研究见Xue 等[6]以及Irion 等[7]。除此，大多数选品相关文章都与顾客选择模型(choice model)有关[8-9]。一方面，大多数关于货架管理的研究仅考虑选品问题[8,10-11]或货架布局问题[2,6-7]，而实际中货架管理包含选品与货架布局两个方面，因此同时决策选品与货架布局尤为关键；另一方面，货架管理的许多研究都基于一组给定的商品，通过将高维货架缩减为一维空间来设计具有空间弹性需求的货架布局，然而其并没有全面考虑零售商要求的商业规则[12-14]与货架复杂结构。

基于目前文献中缺乏同时决策选品与货架布局以及考虑商业规则的相关研究，本研究考虑了某些商业规则，包括商品与货架之间的规格适配性，每一层货架的商品容纳能力以及商品放置的连续性，提出了同时决策选品与货架布局的货架管理模型，目标是最大化期望总收益，约束是满足上述真实商业规则。然而该模型的约束中存在二次项难以直接求解，本研究进一步通过线性化技术将原始货架管理模型转化为整数线性规划模型，并提出与零售价、边际利润以及需求相关的管理启示，以指导零售商进行选品以及设计货架布局：为了获得更高的期望收益，一方面，当需求与边际利润满足某些关系时，随着N增大，决策将由需求导向转变为边际利润导向；另一方面，当需求与零售价满足某些关系时，决策始终是零售价导向的。其优势在于零售商可以直接根据商品历史零售价、边际利润以及需求信息，决策选品以及设计货架布局，而无需求解一个整数规划模型。最后，本研究提出原始货架管理模型的抽样平均近似模型，并给出数值例子验证管理启示。本研究最主要的创新点在于提出了一类多产品多周期的基于报童模型的货架管理模型，其同时考虑了选品与货架布局以及某些真实商业规则。

1 自动售货机的货架管理模型

1.1 问题描述

考虑一个包含J个货架的自动售货机，并且每个货架j都有Kj列空间用于放置商品，其中j∈[J]={1,2,…,J}。总商品类别数量表示为I，货架j上的每一列最多可以放置bij个商品Ci，其中i∈[I]={1,2,…,I}。每个商品Ci的零售价与订购成本分别用pi与ci表示。本研究仅考虑一个销售周期，商品种类以及货架布局决策在一个销售周期内是固定的，且该周期包含T个补货周期，每个补货周期包含N个单位时间（如天，周），因此，N决定了单个补货周期的时间。此外，自动售货机的商品会在每个补货周期t开始时定期补货，补货遵循选品以及货架布局决策，每次补货的固定成本为C0。我们将周期t中单位时间需求表示为，这是一个随机变量。期初，零售企业决策自动售货机售卖商品种类以及货架布局，用y=(yij)i∈[I],j∈[J]表示，其中yij∈Z+是一个整数变量，表示自动售货机货架j上放置商品Ci的列数。

在一个补货周期t中，商品Ci的总需求为，并且根据货架空间分配决策y，每种商品Ci的总库存量为，我们用Z1(d,y)表示在第一个补货期内自动售货机的收益：

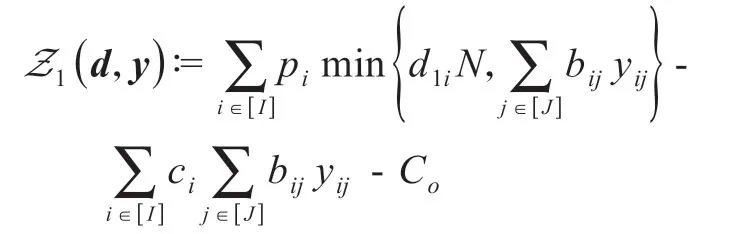
此外，补货周期t∈[2;T]内自动售货机的收益Zt(d,y)表示为：

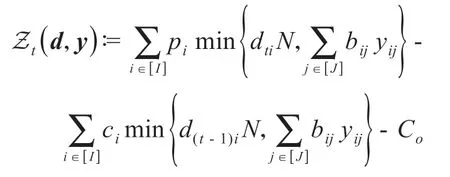
整体上，我们用Z(d,y)表示一个销售周期内的总收益，它是所有补货周期收益的总和：

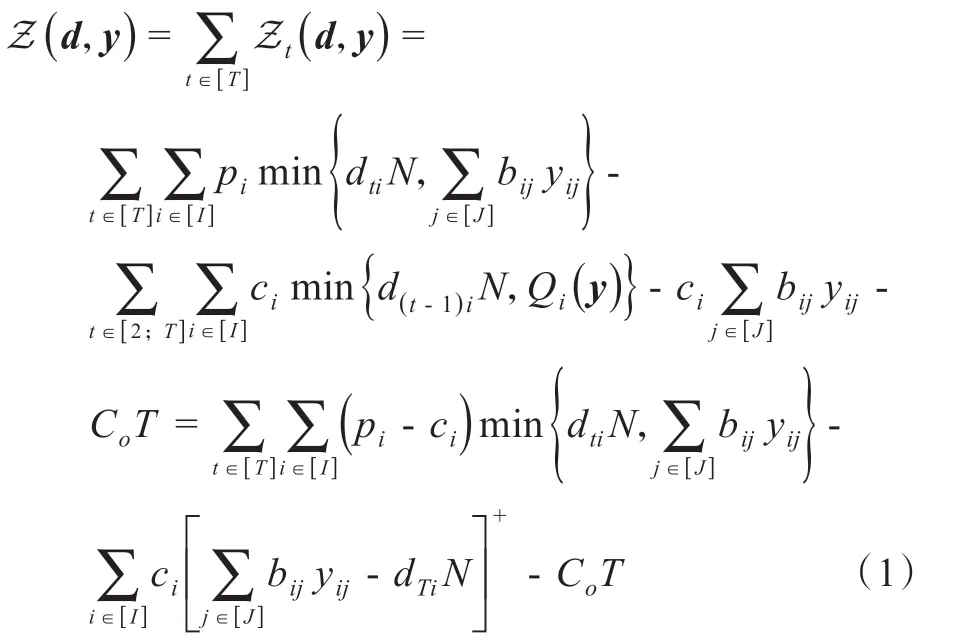
其中[a]+:=max{a,0}。

1.2 商业规则

商业规则1（商品与货架之间的规格适配性）每层货架可以放置不同规格的商品，而某些规格的商品只允许放置在某些货架上，如Bai 等[13]与Düsterhöft 等[15]提出只允许高度比货架高度低的商品放置在该货架上，本研究将其建模为以下约束条件：

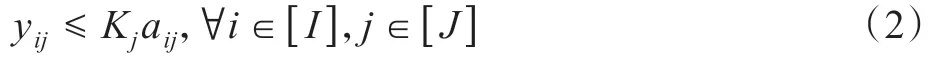
其中aij是一个预先给定的0-1 常数，如果允许商品Ci放置在货架j上，则aij= 1，否则为0；

商业规则2（每层货架的容量）由于每一层货架的空间有限，则需要限制每一层货架放置商品的列数。数学上，将其表示为

商业规则3（商品放置的连续性）考虑到零售商通常希望将同一商品放置在相同的高度上，以呈现较大的吸引力（如Bai 等[13]，Düsterhöft 等[15]），本研究将其建模为以下约束条件：

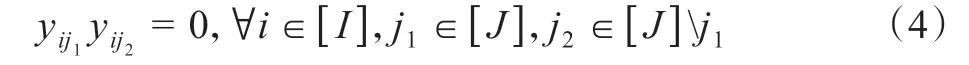
基于上述商业规则1-3，目标为最大化一个销售周期内的总收益函数(1)，本研究提出如下原始货架管理模型：

其中目标函数为最大化一个销售周期内总期望收益；前三个约束分别表示上述3 个商业规则，最后一个约束表明决策变量是一个非负整数，表示自动售货机货架j上放置商品Ci的列数。然而，由于第三组约束中存在决策变量的二次项，该模型难以直接求解，下一节将提出原始货架管理模型的等价整数线性规划模型。

1.3 线性货架管理模型

考虑到原始货架管理模型难以求解，本节将利用线性化技术，引入辅助0-1 决策变量x=(xij)i∈[I],j∈[J]，其中xij= 1 表示自动售货机货架j上放置商品Ci，否则xij= 0，则原始货架管理模型(5)可以等价转化为如下线性货架管理模型

上述等价性由如下命题给出。

命题1.原始货架管理模型(5)等价于线性货架管理模型(6)。

证明：首先，两个模型的目标函数相同且仅与y有关，则证明该命题只需要分别证明其中一个模型的最优解y⋆为另一个模型可行解即可。

一方面，假设y⋆为原始货架管理模型的最优解，令

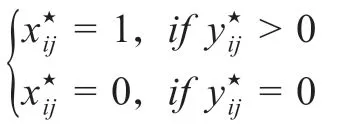
另一方面，假设(y⋆,x⋆)为线性货架管理模型的最优解，根据约束∑j∈[]J xij≤1,∀i∈[I]，对于∀i∈[I]，如果存在j∈[J]使得= 1，则有= 0,∀l∈[J],j≠l，此时，根 据 约 束yij≤Kjxij,∀i∈[I],j∈[J]，则 有y⋆il=0,∀l∈[J],j≠l，此时y⋆满足原始货架管理模型约束条件；否则对于∀j∈[J]，都有= 0，则有= 0，y⋆同样满足原始货架管理模型约束条件，因此y⋆为原始货架管理模型的可行解，命题得证。

2 商品边际利润、零售价与需求对货架管理模型的影响分析

为了获得有关选品以及货架布局的管理启示，本节将分析商品边际利润、零售价与需求对货架管理模型的影响。

实际上，为了获得更高的利润，管理者会从两方面进行决策：一是当补货周期较短时，大部分商品存在剩余，管理者会根据商品历史需求信息，决策选择期望利润较高的商品；而当补货周期较长时，大部分商品售罄，管理者会决策选择边际利润更高的商品。接下来从理论上验证上述观点。

为了简单起见，本节仅考虑单层货架且只能容纳一列商品的特殊情况，且假设各补货周期商品需求相等，令

此时，原始货架管理模型(5)简化为

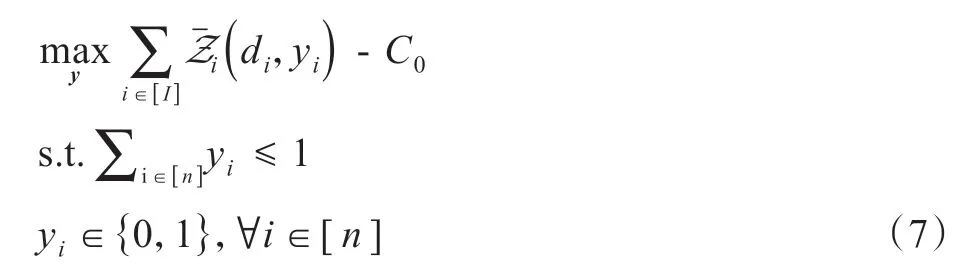
基于上述简化模型，接下来各小节分别讨论当具有相同订购成本与不同订购成本时，商品边际利润、零售价与需求对单个货架商品选择的影响。

2.1 相同订购成本下商品边际利润、零售价与需求对货架管理模型的影响分析

假设存在A,B,C,D共4 类商品，其订购成本均为c，而相应的零售价、边际利润与需求如下

其中p1≥p2,r1≥r2,d1≤d2。如果该货架对四类商品的容纳数量相同，即b ∶= bA= bB= bC= bD，则有或者，其来自于

显然应该首先选择商品A，最后选择商品D，然而商品B与C的选择顺序仍无法确定。接下来，本研究给出以下引理以及定理来说明这两类商品的选择方法，同时揭示了商品选择顺序与商品边际利润、零售价与需求之间的关系。

引理1假设只能容纳一列商品的单层货架上需放置数量b、且满足此列规格的商品B或C，两者的订购成本均为c，且商品B与C的需求与边际利润满足关系

则有

证明：只需要在商品B与C之间选择平均利润更高的商品，其可以表示为

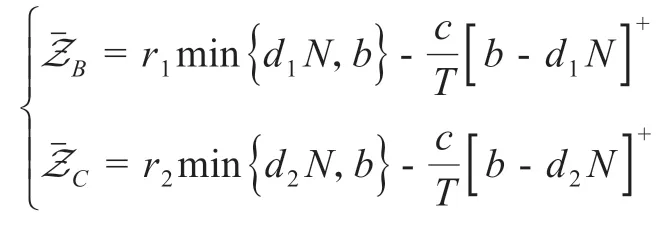
A.如果N≥NB，则有

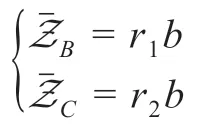
此时，-=(r1- r2)b ≥0，则首先选择边际利润更大的商品B；

B.如果N≤NC，则有

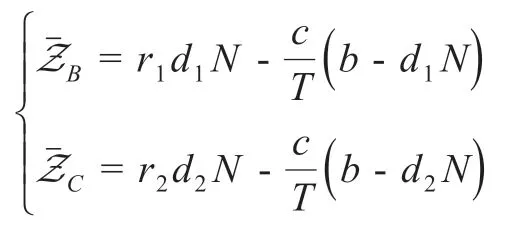
此时，可以得到

因此，在前一种情况下，首先选择边际利润更大的商品B；而在后一种情况下，首先选择需求更高的商品C；

C.如果NB≥N≥NC，则有

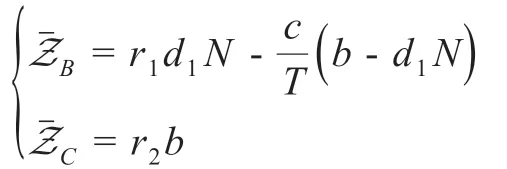
此时，可以得到

考虑以上所有情况，可以得出引理中的结论，引理得证。

管理启示1：为了获得更高的期望收益，当r1d1-时，对于任意N，首先选择边际利润更大的商品B；否则，当N较小时，决策是需求导向的，即首先选择需求更高的商品C，并且随着N增大，决策由需求导向转变为边际利润导向，即首先选择边际利润更大的商品B。

引理2假设只能容纳一列商品的单层货架上需放置数量b、且满足此列规格的商品B或C，两者的订购成本均为c，且商品B与C的需求与零售价满足关系

对于任意N，首先选择零售价更高的商品B。

证明：根据引理假设，可以得到

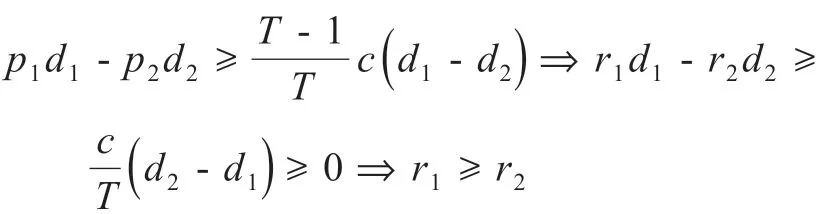
可以根据引理1直接得到该引理结论，得证。

管理启示2：当需求与零售价满足上述关系时，决策始终是零售价导向的，也就是说，对于任意N，都应该首先选择零售价更高的商品B。

引理1 与引理2 仅给出了基于两类商品的管理启示，下面定理1与定理2拓展到多商品的管理启示。

定理1假设只能容纳一列商品的单层货架上需放置数量b、且满足此列规格的商品Ci,i∈[I]，其订购成本均为c，且这些商品的需求d1,…,dI与边际利润r1,…,rI满足关系

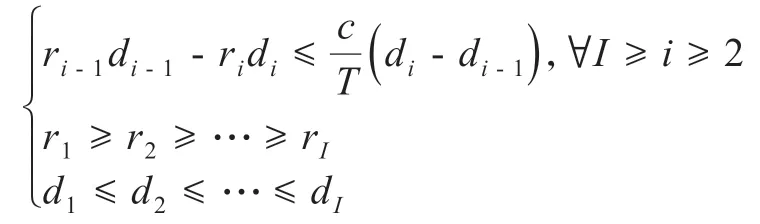
证明：根据定理假设，可以将不等式两边同时叠加得到

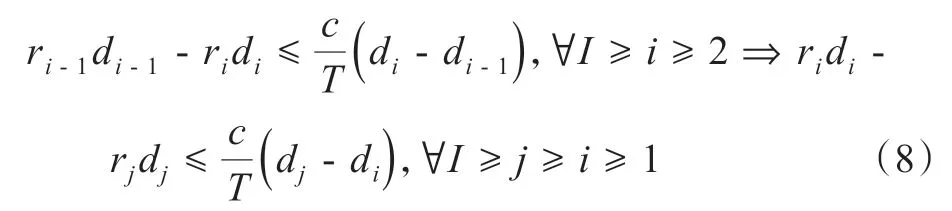
因此，任意一组商品Ci与Cj可以依据引理1 进行选择，此时，可以将N分为三部分来证明定理结论。

根据引理1，首先选择边际利润更大的商品C1；

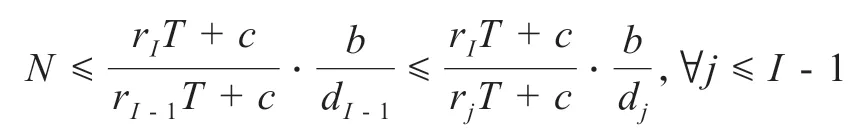
根据引理1，首先选择需求更高的商品CI；

C.如果存在I- 1 ≥i≥2 使得，首先考虑右端不等式，则有

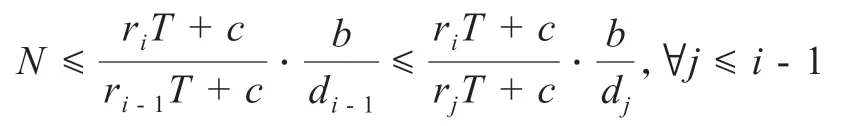
其中第二个不等式成立来自于不等式(8)，根据引理1，对于商品Cj,j∈[i]，首先选择边际利润更大的商品Ci；另一方面，考虑左端不等式，则有

其中第二个不等式成立来自于不等式(8)，根据引理1，对于商品Cj,j∈[i:I]，首先选择边际利润更大的商品Ci，定理得证。

管理启示3：定理1 将引理1 拓展到了多商品的情况，其同样表明为了获得更高的期望收益，随着N增大，决策将由需求导向转变为边际利润导向。

定理2假设只能容纳一列商品的单层货架上需放置数量b、且满足此列规格的商品Ci,i∈[I]，其订购成本均为c，且这些商品的需求d1,…,dI与零售价p1,…,pI满足关系

则对于任意N，首先选择零售价更高的商品C1；此外，如果该货架能容纳K列商品，则选择零售价较高的商品C1,…,CK。

证明：对于任意商品Cj,j∈[2:I]，根据定理条件，则有

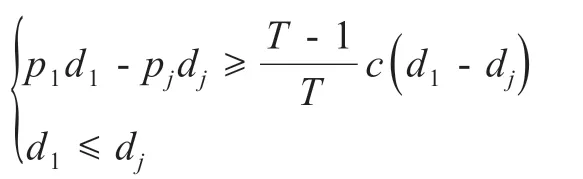
因此任意一组商品C1与Cj可以依据引理2 进行选择，则有对于任意N，首先选择零售价更高的商品C1；如果该货架能容纳K列商品，每次选择一个商品，然后在剩余产品中继续按照上述方法进行选择，最终选择出零售价较高的商品C1,…,CK，定理得证。

管理启示4：定理2 同样将引理2 拓展到了多商品的情况，当需求与零售价满足上述关系时，决策始终是零售价导向的。

2.2 不同订购成本下商品边际利润、零售价与需求对货架管理模型的影响分析

上一节考虑各商品订购成本是相同的，本节将拓展到不同订购成本的情况，并基于上节提出的引理与定理，提出以下推论分析商品边际利润、零售价与需求对货架管理模型的影响。

推论1假设只能容纳一列商品的单层货架上需放置数量b、且满足此列规格的商品B或C，两者的需求、边际利润以及订购成本满足关系

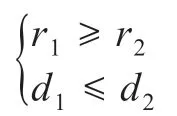
则有

（1）当

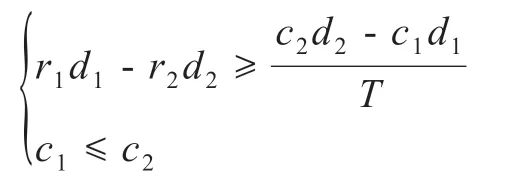
对于任意N，将首先选择边际利润更大的商品B。

（2）当

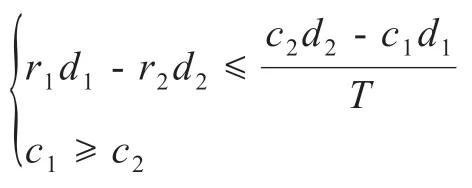
证明：该推论证明方法与引理1证明方法完全类似，因此本研究省略了该部分证明。

推论2假设只能容纳一列商品的单层货架上需放置数量b、且满足此列规格的商品Ci,i∈[I]，这些商品的需求、边际利润以及订购成本满足关系

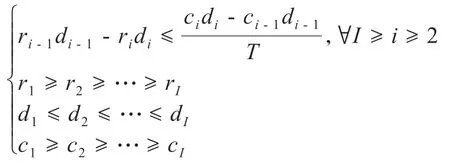
证明：该推论证明方法与定理1证明方法完全类似，因此本研究省略了该部分证明。

推论3假设只能容纳一列商品的单层货架上需放置数量b、且满足此列规格的商品B或C，两者的需求、零售价以及订购成本满足关系

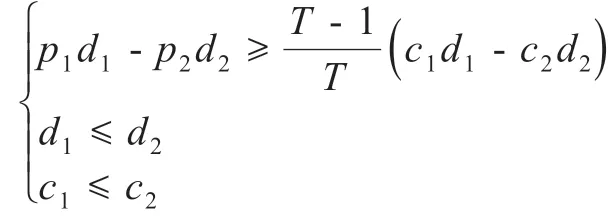
对于任意N，首先选择零售价更高的商品B。

证明：该推论证明方法与引理2证明方法完全类似，因此本研究省略了该部分证明。

推论4假设只能容纳一列商品的单层货架上需放置数量b、且满足此列规格的商品Ci,i∈[I]，这些商品的需求、零售价以及订购成本满足关系

则对于任意N，首先选择零售价更高的商品C1；此外，如果该货架能容纳K列商品，则选择零售价较高的商品C1,…,CK。

证明：该推论证明方法与定理2证明方法完全类似，因此本研究省略了该部分证明。

上述推论将上一节引理与定理拓展到订购成本不同的情形。

管理启示5：为了获得更高的期望收益，一方面，当需求与边际利润满足某些关系时，随着N增大，决策将由需求导向转变为边际利润导向；另一方面，当需求与零售价满足某些关系时，决策始终是零售价导向的。

3 实验研究

本节将提出原始货架管理模型的抽样平均近似模型，并设计数值实验验证管理启示。

3.1 抽样平均近似模型

首先，根据命题1，原始货架管理模型(5)等价转化为

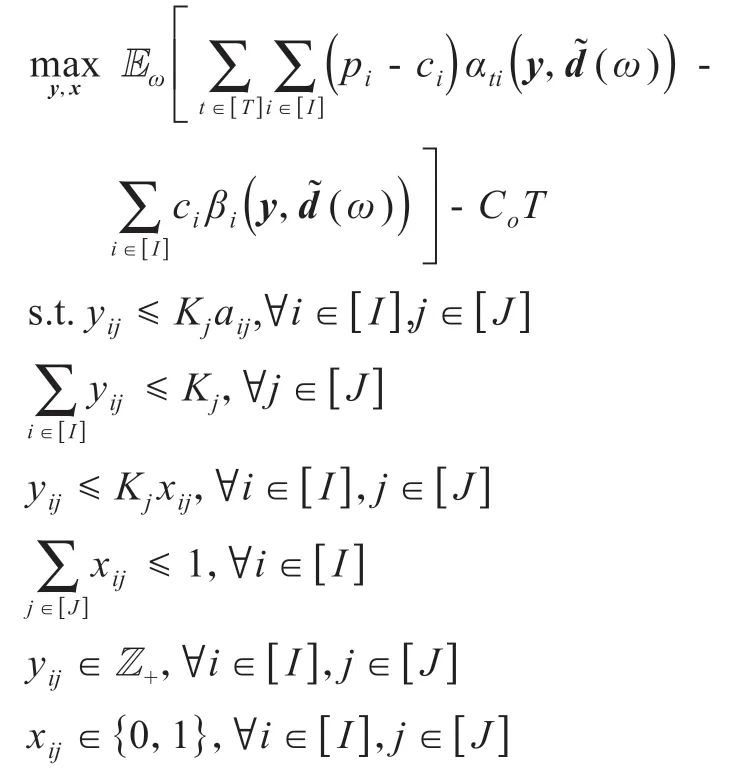
其中

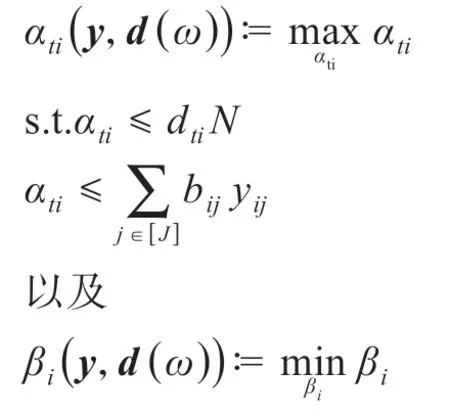
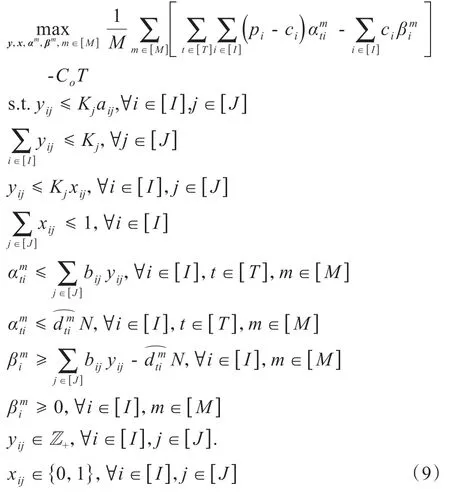
3.2 数值例子

本节将利用零售企业便利蜂某门店的真实销售数据设计数值实验，其包含了2019年下半年该门店自动售货机销售的部分商品品类、零售价、边际利润以及需求量等数据，进一步基于这些样本求解抽样平均近似模型(9)并验证管理启示。

首先表1给出了自动售货机的基本设置：自动售货机有5层货架，且每层货架的商品容纳列数不同；每一列可以容纳不同数量的商品。假设固定补货成本C0= 10。

表1 自动售货机的规格

令总补货周期T= 7，接下来调整N∈{1,5,9}，图1与图2分别给出样本平均近似模型最优决策所选商品的边际利润与平均需求、零售价与平均需求之间的关系，其中横坐标表示商品平均需求，纵坐标分别表示商品的边际利润与零售价。

图1与图2均验证了管理启示5：随着N增大，所选商品由右下向左上移动，其反映了N较小时，模型首先选择需求较高的商品，随着N增大，决策由需求导向转变为边际利润或零售价导向，此时选择边际利润或零售价较高的商品，同时表明单货架的管理启示可以拓展到多货架的情形。该结果在实际中也是合理的：当N较小时，单个补货周期的周期短，大多数商品售罄前就开始补货，此时模型倾向于选择高需求商品，以达到薄利多销获取更高利润；而随着N增大，单个补货周期的周期短，大多数商品售罄，此时模型倾向于选择高边际利润或零售价的商品，以获取更高利润。

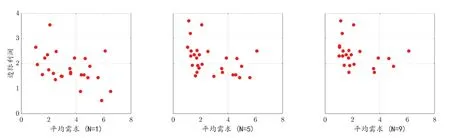
图1 抽样平均近似模型最优决策所选商品的边际利润与平均需求之间的关系图

图2 抽样平均近似模型最优决策所选商品的零售价与平均需求之间的关系图

为了进一步展示抽样平均近似模型最优决策所选商品的特征，图3给出了不同N下所选商品的平均零售价、平均边际利润以及平均需求变化情况：随着N增大，所选商品平均零售价以及平均边际利润增大，同时所选商品平均需求降低，进一步验证了随着N增大，决策将由需求导向转变为零售价导向以及边际利润导向。

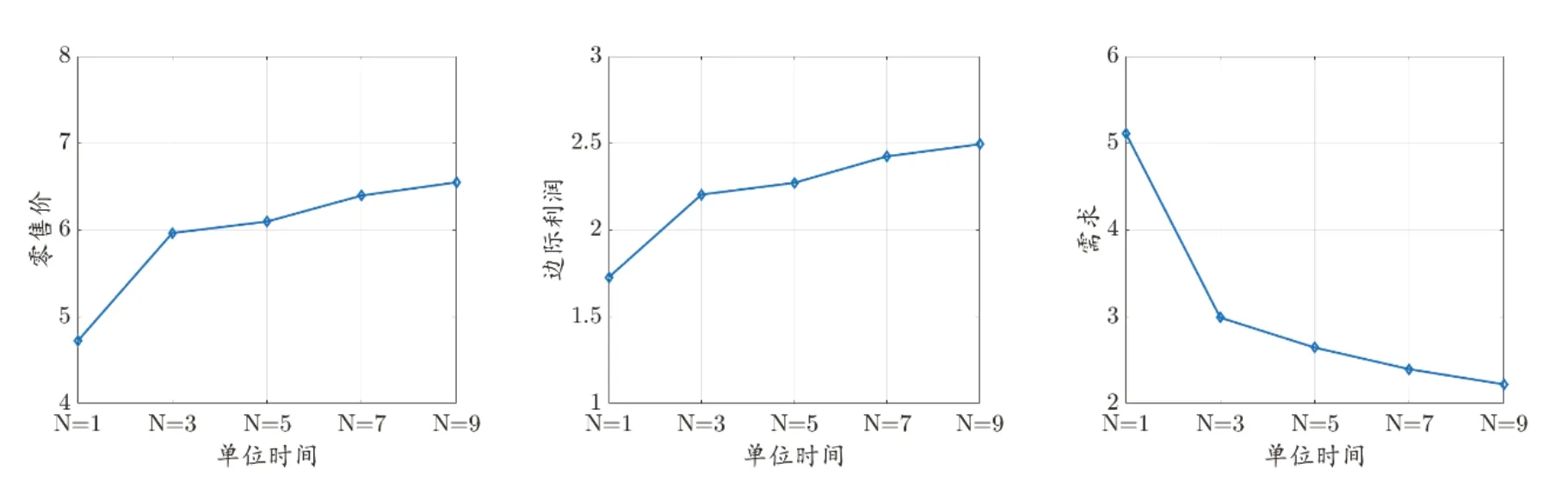
图3 不同N下抽样平均近似模型最优决策所选商品的平均零售价、平均边际利润以及平均需求的变化图

4 结语

本研究基于一些真实商业规则，包括商品与货架之间的规格适配性、每一层货架的商品容纳能力以及商品放置的连续性，提出了同时决策选品与货架布局的货架管理模型，目标是最大化期望总收益。然而该模型的约束中存在二次项难以直接求解，本研究进一步通过线性化技术将原始货架管理模型转化为整数线性规划模型，并提出与零售价、边际利润以及需求相关的管理启示，以指导零售商进行选品以及设计货架布局：一方面，当需求与边际利润满足某些关系时，随着N增大，决策将由需求导向转变为边际利润导向；另一方面，当需求与零售价满足某些关系时，决策始终是零售价导向的。其优势在于零售商可以直接根据商品历史零售价、边际利润以及需求信息，决策选品以及设计货架布局，而无需求解一个整数规划模型。最后，本研究提出原始货架管理模型的抽样平均近似模型，并给出数值例子验证管理启示。实际中，商品需求存在不确定性，并且其直接影响管理决策，而本研究缺乏对需求不确定性的建模与处理，因此如何引入需求不确定性值得进一步研究。针对该问题，未来可以从两个方向进行深入研究，一方面是利用鲁棒优化技术建立鲁棒优化模型，另一方面是引入顾客选择模型，并将其嵌入货架管理模型。