氯盐锈蚀钢框架柱抗震性能试验及恢复力模型研究

董晋琦 ，郑山锁 ，张晓辉，尚志刚，刘 毅，王 斌

(1. 西安建筑科技大学土木工程学院，西安 710055；2. 西安建筑科技大学结构工程与抗震教育部重点实验室，西安710055；3. 西安工业大学建筑工程学院，西安710021)

由于环境因素的影响，钢结构的服役环境不断恶化，造成钢结构的力学性能受到极大影响，尤其是在地震作用下，钢结构因锈蚀影响导致的破坏更为严重．而现行抗震设计规范的计算模型并没有考虑受锈蚀影响钢结构的抗震性能，且钢结构在设计使用年限内难以进行防锈蚀维护[1]．

目前，国内外对锈蚀钢结构的材料层面进行了大量研究，锈蚀可导致钢材截面减小、力学性能下降，且锈蚀产生的腐蚀坑会造成应力集中现象[2-4]．但关于锈蚀对钢结构影响的研究不能仅停留在材料层面，更需要深入研究锈蚀对结构或构件的承载力与抗震性能的影响[5]．恢复力模型是结构弹塑性反应分析的基础，Ibarra和Krawinkler提出了考虑了构件强度、刚度退化对构件影响的Ibarra-Krawinkler(I-K)本构关系模型[6]；郭子雄等[7]研究了不同轴压比对框架柱滞回特性的影响．恢复力模型的选取对结构弹塑性分析的结果具有重要影响[8-10]．

鉴于此，本文利用人工气候环境法对48件钢材试件及4榀钢框架柱试件进行人工加速锈蚀，并进行了材性拉伸试验及钢框架柱低周往复加载试验，研究了氯盐锈蚀对钢结构力学性能与抗震性能的影响．在此基础上，建立了考虑氯盐锈蚀影响的钢框架柱恢复力模型，并与试验结果进行对比验证．研究成果为锈蚀钢框架结构抗震性能评估提供了依据．

1 试验概况

1.1 试件设计

本试验试件按照《钢结构设计规范》(GB 50017—2017)、《建筑抗震设计规范》(GB 50011—2010)等现行规范和规程进行设计，采用1∶2缩尺比例设计4榀钢框架柱试件．试验模型取钢框架结构在水平荷载作用下，节点到上、下柱反弯点的典型单元为研究对象．各试件材料选材均为Q235钢，热轧H型钢，型钢截面为HW250mm×250mm×9mm×14mm．试件尺寸见图1，轴压比为0.3．采用人工气候环境法对试验钢框架柱进行加速锈蚀并进行低周往复加载试验．

1.2 锈蚀环境模拟

在役钢结构受氯离子侵蚀是自然环境中钢结构锈蚀的主要原因[11]．氯离子侵蚀环境模拟装置采用ZHT/W2300气候模拟试验系统，如图2所示．具体参数依据《人造气氛腐蚀试验——盐雾试验》(GB/T 10125—2012)[12]相关规定进行设定.氯离子侵蚀环境采用质量分数为5%的氯化钠溶液模拟，腐蚀箱内温度设置为35℃，湿度控制为95%以上，pH值设置为6.5～7.5，喷淋每次间隔10min，单次喷淋时间5min，盐雾沉降量为1～2mL/(80cm²·h)．

钢结构在氯离子侵蚀作用下，侵蚀时间的长短会导致结构产生不同的锈蚀程度．为此，试验设置4种不同锈蚀程度的试件，试件编号为KZ-1～KZ-4，锈蚀时间分别为0h、960h、1920h和2880h，并引用失重率参数对锈蚀程度进行量化，分别为0、3.06%、5.33%和8.02%．失重率DW为锈蚀前、后钢框架柱质量的差值与锈蚀前质量的比值．

1.3 加载制度及加载装置

图3 试验加载装置Fig.3 Test loading device

低周往复加载试验加载装置如图3所示．试验采用液压千斤顶在柱顶施加竖向荷载至设计轴压比后保持不变，由30t的MTS电液伺服作动器提供施加在框架柱顶端的水平低周往复荷载．结合钢结构抗震规范[13]，加载制度采用位移进行控制，按照层间位移角为0.375%、0.500%、0.750%、1.000%、1.500%、2.000%进行递增，此后层间位移角增量均为1.000%，每级循环加载均为2次，当加载进行到承载力下降至最大荷载值的85%则停止加载．具体试验加载流程如图4所示．试验加载端位移计和荷载数据信息均由MTS数据采集系统自动采集．

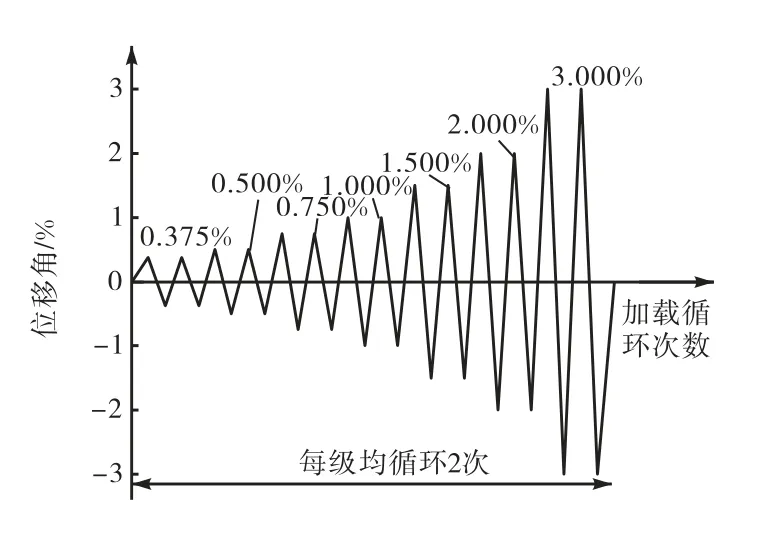
图4 试验加载流程Fig.4 Test loading process

1.4 材性试验

为得到钢材受锈蚀影响力学性能的退化规律，根据《钢及钢产品力学性能试验取样位置及试样制备》(GB/T 2975—2018)要求，本文对6.5mm、9.0mm及14.0mm 3种厚度共48件的标准试件进行了加速锈蚀及材性试验．试件材料选取Q235B钢材，加速锈蚀试验与4榀钢框架柱所处环境相同．48件试件锈蚀时间均为0h、240h、480h、960h、1440h、1920h、2400h、2880h．不同厚度钢材随锈蚀时间与失重率之间的关系如图5所示，可以看出：厚度越小的钢材在相同锈蚀时间下，失重率越高.

力学性能试验数据如表1所示．由表1可知，随着失重率的逐渐增大，钢材试件的各项力学性能指标均有所下降，屈服强度、极限强度、延伸率、弹性模量最大下降幅度分别为12.78%、12.78%、21.13%、13.28%，且相同锈蚀时间下，厚度越小的试件，力学性能劣化程度越明显．

引用失重率参数对锈蚀程度进行量化，对试验数据进行回归分析，得到不同锈蚀程度钢材的屈服强度、极限强度、延伸率和弹性模量与失重率之间的关系，如图6所示．

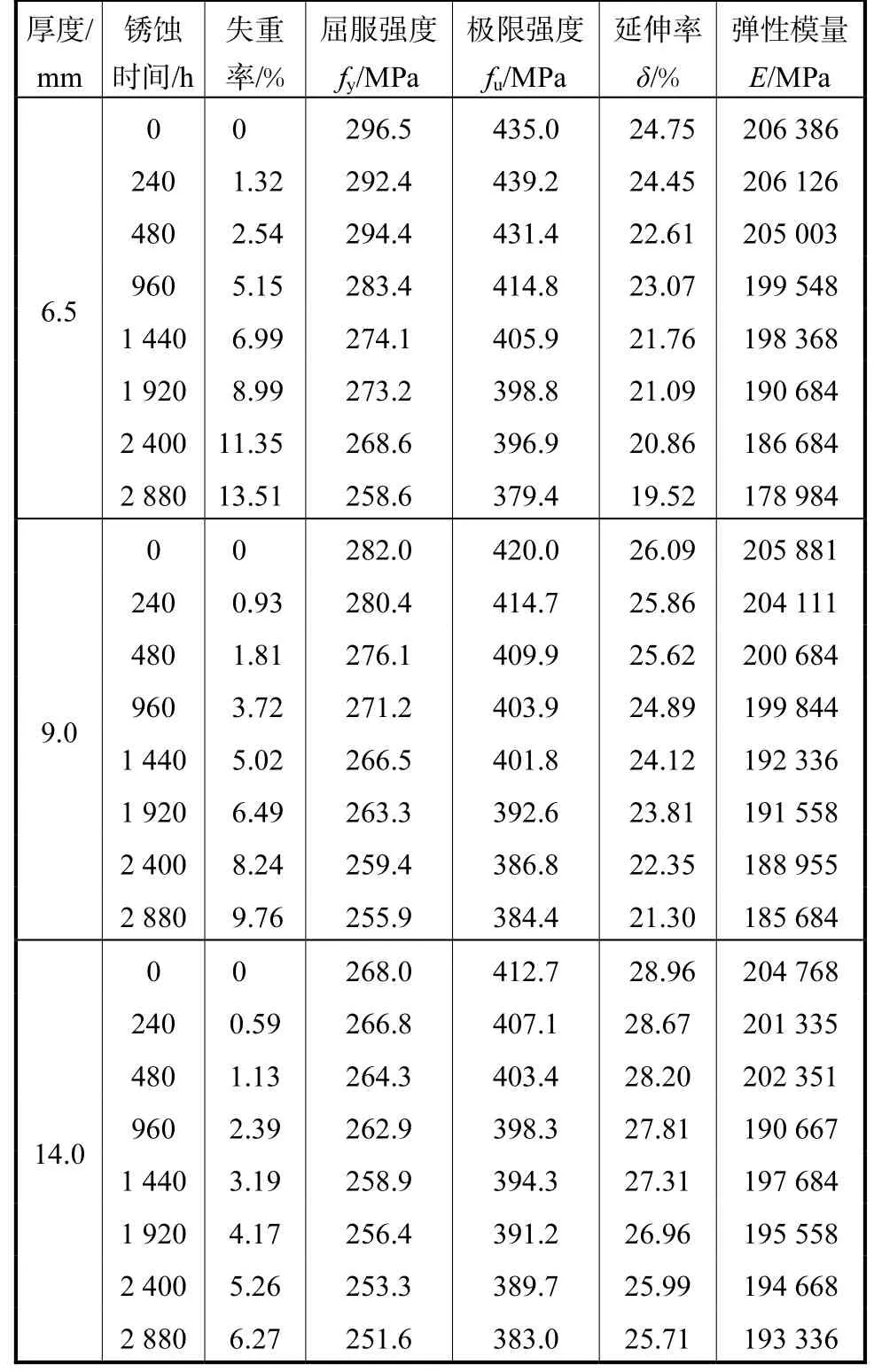
表1 钢材的力学性能Tab.1 Mechanical properties of steel

由图6可以看出，钢材各力学性能指标与失重率近似呈线性关系，各力学性能指标随着失重率的增加均呈现出不同程度的退化规律．回归曲线的数学表达式为

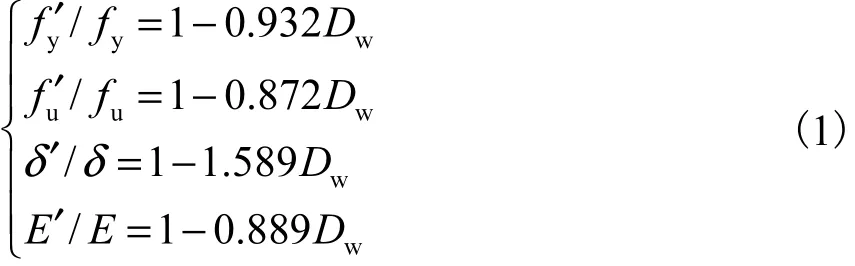
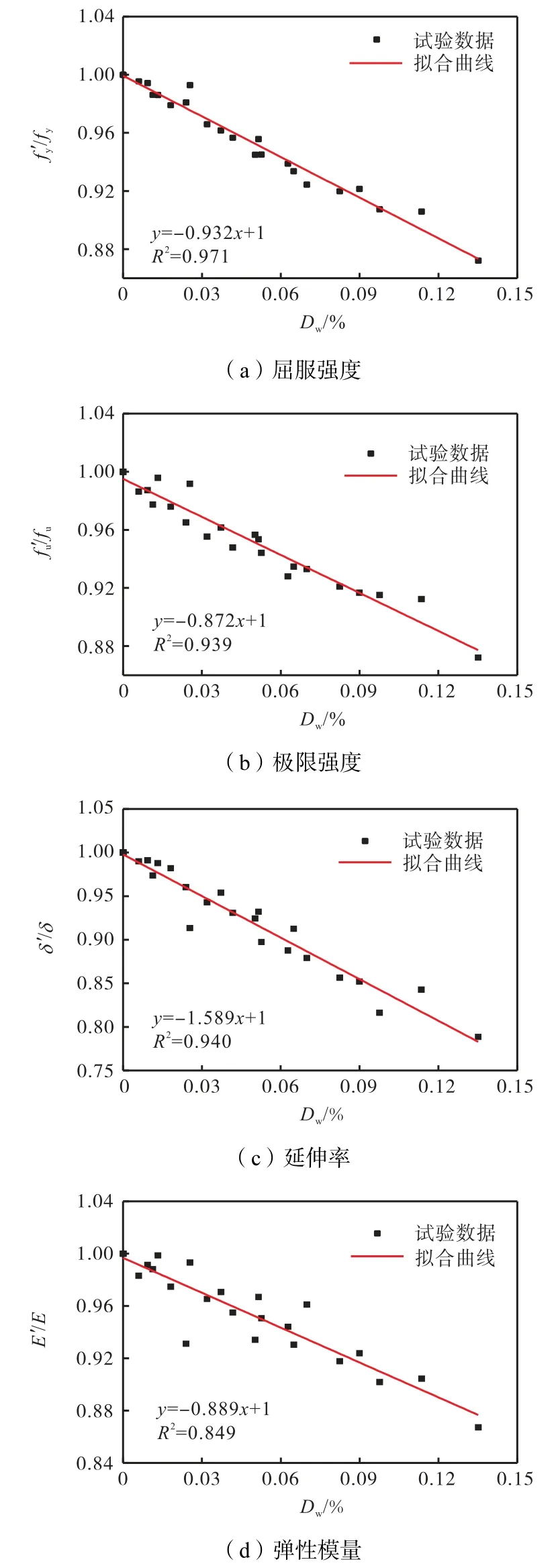
图6 钢材力学性能指标与失重率之间的关系Fig.6 Relationship between the mechanical properties of steel and weight loss rate

2 试验结果及其分析

2.1 滞回曲线

滞回曲线可以综合反映构件在受力过程中的变形性能和抗震性能的变化规律[14-15]．试件滞回曲线如图7所示．

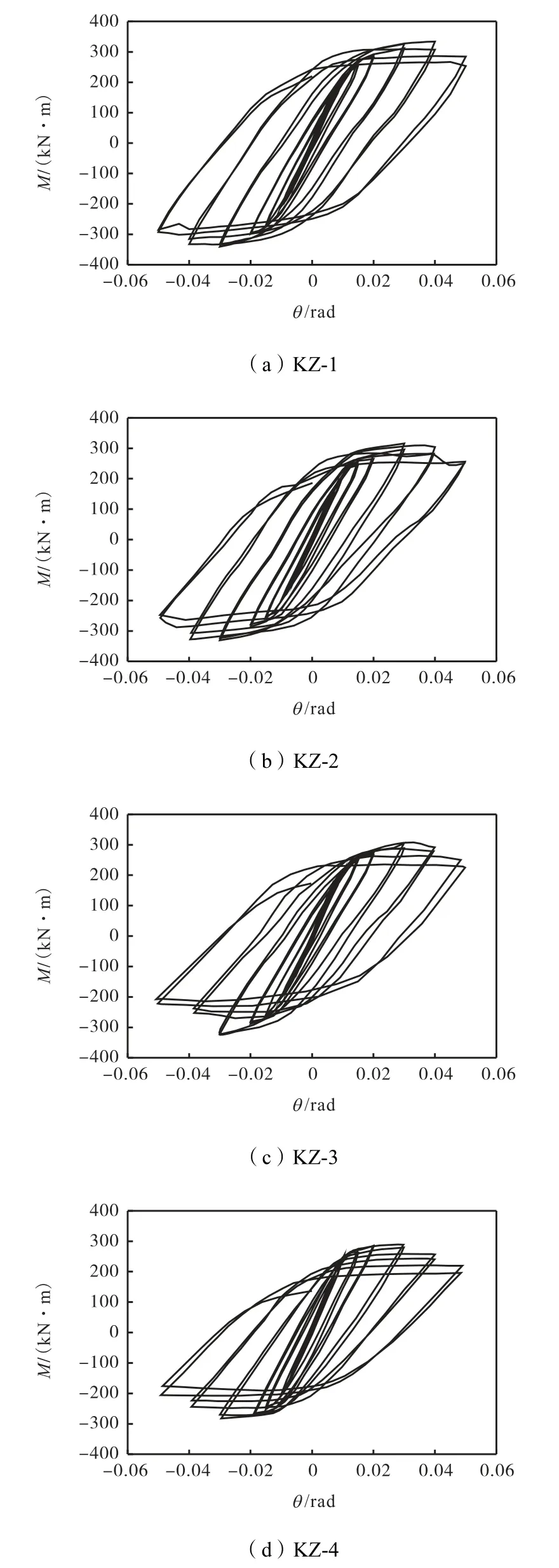
图7 试件滞回曲线Fig.7 Hysteretic curves of specimens

根据图7，可以得出如下结论．

(1) 4榀钢框架柱试件的滞回性能基本相似．在加载初期阶段，各试件基本处于弹性状态，加卸载时的滞回曲线近似呈直线；随着加载的进行，滞回环面积开始增大，表明试件开始发生塑性变形，滞回曲线的斜率开始减小，试件承载力仍呈增大趋势；加载达到峰值荷载后，滞回曲线的斜率随加载控制位移的增大而减小，滞回环面积逐渐减小，这表明试件的塑性变形充分发展，各项性能指标随层间位移角和循环加载次数的增加退化明显；当试件加载至破坏阶段时，试件的承载力迅速降低，试验加载随之结束．

(2) 4榀钢框架柱试件的滞回曲线均为梭形，曲线所围成的面积较大，且当加载至峰值荷载时，滞回曲线并无捏拢收缩现象，表明锈蚀钢框架柱试件的抗震能力及延性较好．但随着构件锈蚀程度的增加，试件的承载力不断降低，强度、刚度退化现象明显，且滞回环面积逐渐缩小，表明试件的抗震性能在逐渐减弱．

2.2 骨架曲线

骨架曲线是结构弹塑性分析的重要依据[14]．通过对比图8各试件的骨架曲线，可以看出各试件骨架曲线的总体形状相似：在加载初期时，各试件的骨架曲线基本重合；当加载至弹塑性阶段，各试件随锈蚀程度的增加曲线的斜率逐渐减小，骨架曲线承载力峰值也在逐渐降低，且随锈蚀程度的加剧，降低程度愈明显．

图8 试件骨架曲线Fig.8 Skeleton curves of specimens

2.3 承载力和延性系数

试件实测特征值及位移延性系数如表2所示．从表2中可以看出，各试件的承载力及延性系数随试件失重率的增加而降低，锈蚀程度越严重，承载力及延性系数的下降速率越大．当失重率从0增加到8.02%时，峰值弯矩、极限转角和延性系数分别降低了17.34%、24.21%和12.32%．

对表2中以不同失重率为设计变量的试验数据进行回归分析，得到锈蚀钢框架柱抗震性能特征参数的退化规律，如图9所示．

相应的回归公式为

表2 试件实测特征值和延性系数Tab.2 Experimental characteristic values and ductility coefficients of the specimen

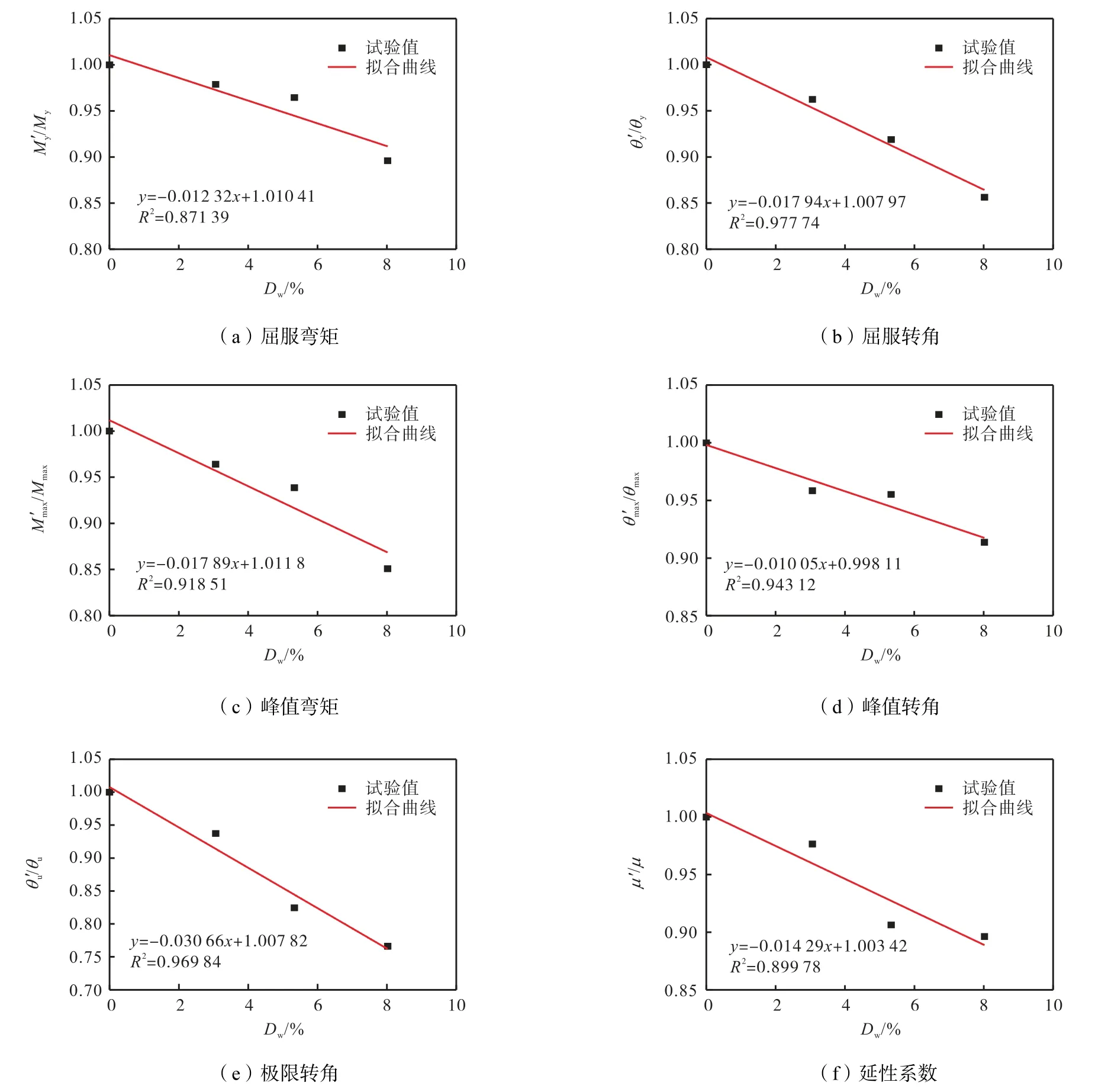
图9 试件抗震性能特征参数退化规律Fig.9 Degradation law of the characteristic parameters of seismic performance of specimens

2.4 强度衰减与刚度退化

试件强度衰减曲线可反映试件承受往复荷载的能力[16]．图10为试件强度衰减曲线．通过对比分析可知：各试件的强度衰减规律总体一致，随着循环次数的增加，承载力逐渐提高，然后趋于平缓，最后产生强度衰减现象，当失重率增加时，试件强度衰减现象更加明显．

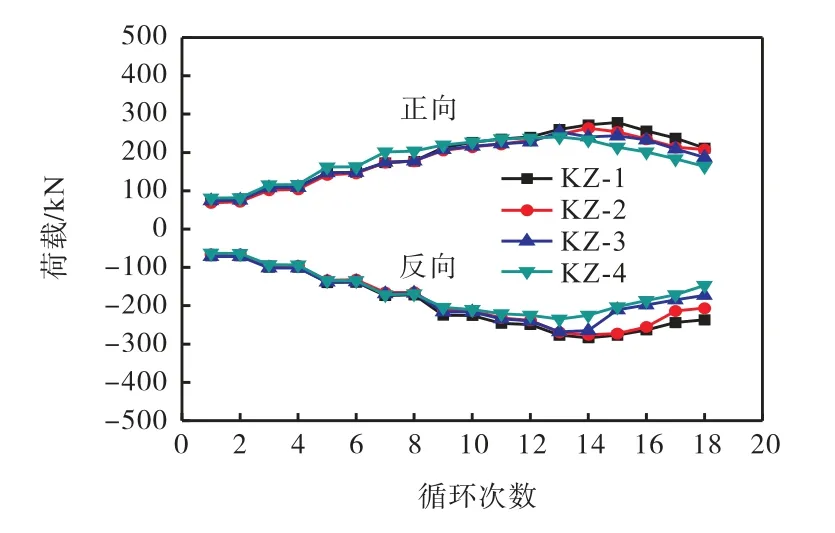
图10 试件强度衰减曲线Fig.10 Strength degradation curves of specimens

图11为试件等效刚度退化曲线，各试件刚度总体退化趋势基本一致．随着位移加载的进行，刚度退化速率由较快趋于缓慢，失重率越大的试件刚度退化速率越快．

图11 试件等效刚度退化曲线Fig.11 Stiffness degradation curves of specimens

2.5 耗能能力

结构的抗震性能也可以通过耗能能力进行评价．图12为试件的累积耗能曲线．由图可知，各试件累积耗能变化趋势总体保持一致，随着加载的进行，累积耗能增加逐渐变快．但锈蚀会影响各试件的耗能能力，当完好试件的失重率变为3.06%、5.33%和8.02%时，累积耗能分别降低了3.07%、14.01%、18.64%．

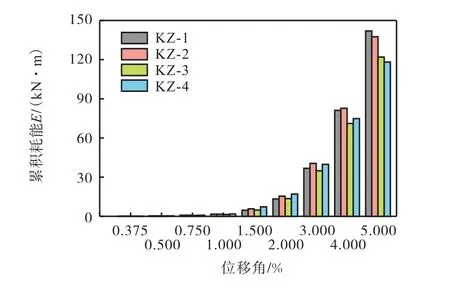
图12 试件累积耗能曲线Fig.12 Cumulative energy dissipation curves of specimens

3 恢复力模型

恢复力模型是一种经过简化的数学模型，主要包括骨架曲线和滞回规则两部分内容，是结构弹塑性分析的基础[17]．本文基于Lignos等[6]和Ibarra等[18]提出的修正Ibarra-Krawinkler(I-K)模型来建立锈蚀钢框架柱构件的弯矩-转角恢复力模型．

3.1 钢框架柱骨架曲线参数的确定

修正I-K模型的骨架曲线的上升段(弹性变形阶段)由屈服弯矩My和初始刚度Ke确定；强化阶段根据Ks＝αsKe来确定该阶段的刚度，用峰值前塑性转角θp表示相应的变形能力；软化阶段通过软化段刚度Kc＝αcKe以及峰值后塑性转角θpc共同确定．图13为修正I-K模型的骨架曲线．Ke为初始刚度，My为屈服弯矩，Mmax为峰值点弯矩，θp为峰值前塑形，θpc为峰值后转角，λres为残余强度比．

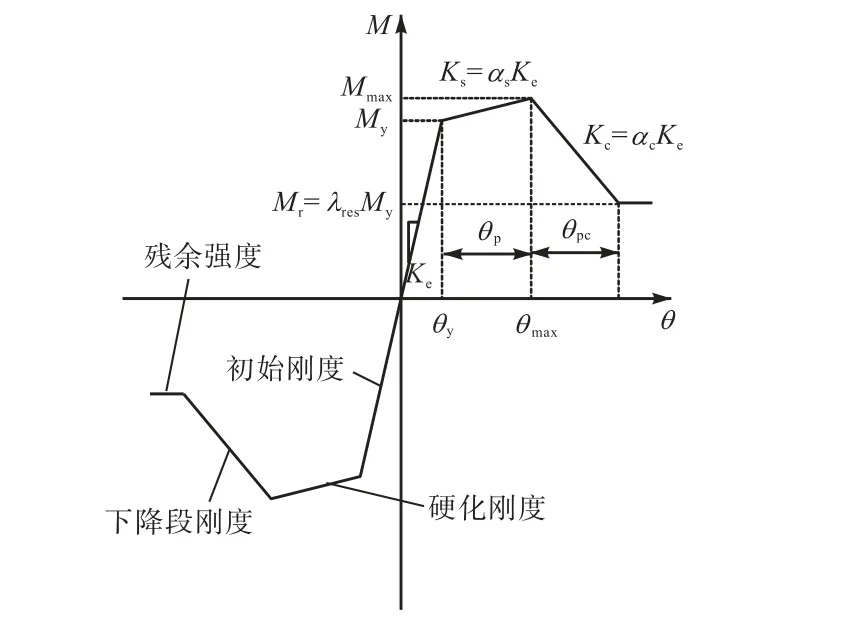
图13 修正I-K模型的骨架曲线Fig.13 Skeleton curve of the modified I-K model

钢框架柱试件的弯矩-转角恢复力模型骨架曲线上屈服点、峰值点和极限点参数的计算如下．

1) 屈服点

参考ASCE/SEI 41-06，钢框架柱的屈服弯矩My和屈服转角θy分别为

式中：Mp为全截面屈服弯矩；N为柱轴压力；An为净截面面积；fy为钢材屈服强度；Wp为塑性截面模量；E为钢材弹性模量；I为截面惯性矩；L为柱计算高度．

Lignos和Krawinkler根据试验，指出钢柱的屈服弯矩My可取值为1.17Mp．此外，由于在试验过程中钢柱与底端的底梁无法形成完全刚结，达不到理想约束条件，导致试验所得刚度偏低．综上，结合本文试验结果，屈服弯矩和屈服转角分别为

2) 峰值点

本文结合Lignos和Krawinkler提出的钢柱峰值弯矩和试验结果，建议峰值弯矩取值为

同时，Lignos和Krawinkler提出钢梁峰值前塑性转角θp的经验公式为

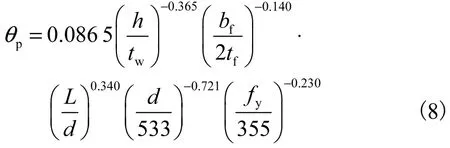
式中：h/tw为腹板高厚比；bf/(2tf)为翼缘宽厚比；d为截面高度；L/d为试件跨高比．

在较小轴压比的情况下，可采用式(8)近似估算钢框架柱的峰值前塑性转角θp．

3) 极限点

极限弯矩Mu可取值为峰值弯矩Mmax的85%，即

同时，Lignos和Krawinkler提出钢梁的峰值后塑性转角θpc的经验公式为

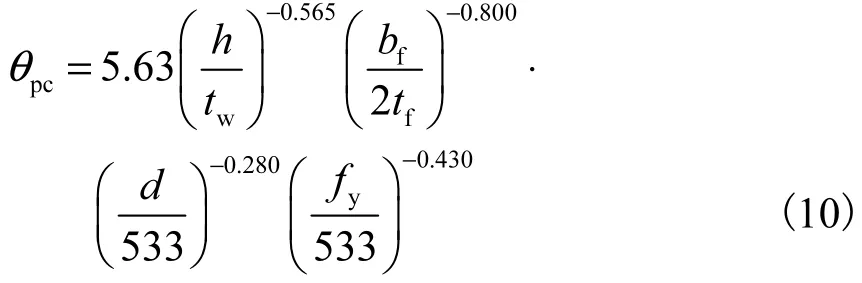
在较小轴压比的情况下，可采用式(10)近似估算钢框架柱的峰值后塑性转角θpc．

根据试验数据统计回归得到钢框架柱抗震性能特征参数(屈服弯矩、屈服转角、峰值弯矩、峰值转角和极限转角)随锈蚀程度变化的退化规律，见表3．

表3 锈蚀试件骨架曲线特征点的拟合公式Tab.3 Fitting formula for characteristic points of the skeleton curve of corroded specimens

3.2 钢框架柱滞回规则

由试验结果可知，锈蚀构件与完好构件恢复力模型形状相似．本文基于修正I-K滞回模型来考虑不同锈蚀程度构件恢复力模型的滞回规则，其循环退化规则如图14所示．

1) 循环退化指数

通过引入Rahnama-Hazaveh等[19]提出的循环退化指数来体现构件各项性能的退化，即

式中：c表示循环退化速率，取c＝1.0；Ei表示构件在第i次循环加载时的滞回耗能表示构件在第i次及第i次之前所有循环下的累积耗能；Et为构件本身的滞回耗能能力，其可表示为屈服强度My与累积转动能力Λ的乘积，其计算式为

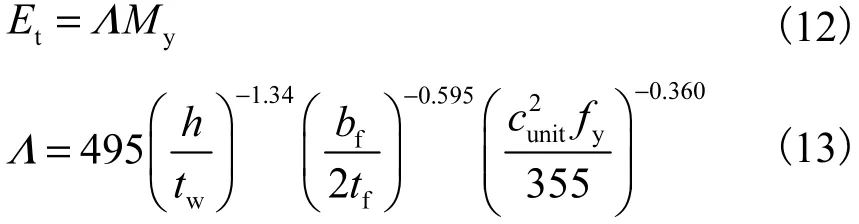
式中：h/tw为腹板宽厚比；bf/tf为翼缘宽厚比为单位转换系数，单位采用mm和MPa时，取值为1．

随着失重率的增加，试件的承载力有所下降，循环退化效应呈增大趋势，但并不显著．因此，对于锈蚀钢框架柱恢复力模型的循环退化速率与未锈蚀构件保持一致，取c＝1.0；累积转动能力Λ仍可按式(13)计算确定．

2) 基本强度退化规则

构件的基本强度退化规则如图14(a)所示．屈服强度和强化段刚度的退化规则计算公式为

3) 峰值后强度退化规则

图14(b)为构件的峰值后强度退化规则．峰值后强度的退化规则计算式为

4) 卸载刚度退化规则

构件在进入屈服阶段后，卸载刚度也出现退化现象，退化规则如图14(c)所示，计算式为

式中Kui和Ku(i-1)分别表示构件第i次和第i－1次加载时的卸载刚度．

3.3 钢框架柱恢复力模型的验证

通过OpenSEES软件建立锈蚀钢框架柱的集中塑性铰模型，如图15所示．将钢框架柱简化为弹性杆单元和位于柱底部的非线性转动弹簧单元串联模型．弹性杆单元采用OpenSEES软件中弹性梁柱单元(elasticBeamColumn)模拟；非线性转动弹簧单元由零长度单元(zeroLength)模拟，并通过上文所确定的骨架曲线特征点和滞回规则来计算Bilin Material的参数，用以标定零长度单元．相关参数计算结果如表4所示．

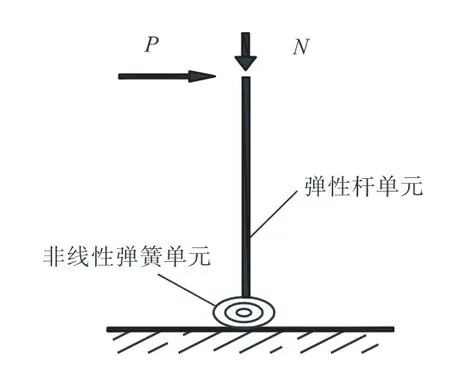
图15 钢框架柱集中塑性铰模型Fig.15 Concentrated plastic hinge model for a steel frame column

表4 锈蚀钢框架柱恢复力模型相关参数Tab.4 Related parameters of the restoring force model of the corroded steel frame column

将上述模型模拟结果与试验结果进行对比分析，两者基本吻合，如图16和图17所示．

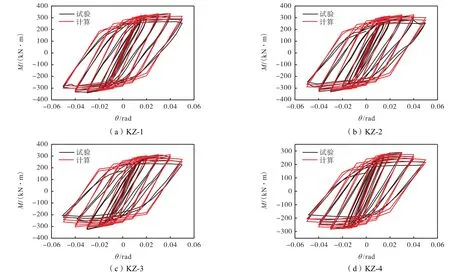
图16 计算滞回曲线与试验滞回曲线对比Fig.16 Comparisons of calculated and experimental hysteretic curves

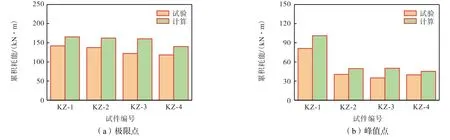
图17 计算累积耗能与试验累积耗能对比Fig.17 Comparisons of calculated and experimental cumulative energy consumptions

4 结 论

(1) 从试验结果可以发现，锈蚀对钢结构的力学及抗震性能具有较大影响，具体表现如下：随着锈蚀程度的增加，钢材的力学性能(屈服强度、极限强度、延伸率和弹性模量)退化明显，且钢材厚度越小，性能退化越显著；钢框架柱的强度、刚度、延性及耗能等随着锈蚀程度的增加逐渐降低，如当失重率为8.02%时，峰值弯矩、极限转角、延性系数和累积耗能能力分别降低了17.34%、24.21%、12.32%和18.64%．

(2) 基于试验结果，以失重率为参数对钢框架柱骨架曲线各特征点弯矩、转角及延性系数拟合，得到了考虑锈蚀影响的钢框架柱骨架曲线特征参数修正函数．

(3) 基于修正I-K模型，结合试验数据，建立可表征基本强度退化、峰值后强度退化、卸载刚度退化等滞回规则的锈蚀钢框架柱恢复力模型，通过与试验结果的对比，验证本文所建立恢复力模型的有效性．研究成果可为锈蚀钢框架结构的非线性地震反应分析提供理论依据．