基于稀疏贝叶斯-RNAMBO算法的低剂量CT盲复原方法

刘晓培 ，滕建辅，费 腾，孙云山

(1. 天津大学电气自动化与信息工程学院，天津 300072；2. 天津商业大学信息工程学院，天津 300134；3. 天津大学微电子学院，天津 300072)

大量的研究已证实高剂量的X射线辐射会导致癌症、白血病或其他遗传疾病[1-3]．减少CT检查时X射线的剂量，并且在不牺牲临床诊断信息的前提下对低剂量CT进行复原重建，是许多学者研究的新领域．在CT成像过程中要减少X射线的辐射剂量，有降低投影视角和降低管电流强度两种方法，这会使投影数据的数目少于重建CT图像所需的像素数目，并且CT图像混入大量量子噪声难以去除，此种情况下，点扩散函数和噪声难以估计，CT图像复原变成欠定问题，在图像重建过程中通常要利用先验信息约束解空间，因此，降低重建过程对投影数据的依赖，实现精确的低剂量医学CT重建具有重要的医学价值和应用前景．

由于CT图像采样过程中，受模糊退化与系统噪声影响，如何从众多解中选出最优解，将观测得到的退化图像恢复近似于原始图像，是图像盲复原的最终目标．一些文献使用图像盲复原方法来消除点扩散函数的影响[4-6]．由于CT扫描系统的点扩散函数往往是未知的，针对点扩散函数估计比较困难的问题，卜丽静等[7]在待分析的图像中基于近似点成像特点的基础上，提出了基于特征信息的椭圆抛物面模型，将分离图像信号和噪声的稀疏归一化约束模型引入复原算法．苏畅等[8]将图像分割成多张子图像，构建了一种自适应图像盲复原方法，此方法采用二分法建立约束方程，峰值信噪比有所改善，但仅针对高斯类模糊复原．盲图像反卷积是一个典型的病态反问题，需要额外的信息来约束解空间，由于优化模型的复杂性，Chen等[9]提出了一种新的基于广义lp/lq范数的盲图像反卷积方法，可以获得较高的图像复原质量．Tao等[10]提出了一种基于张量及奇异值分解的改进FBP算法，该算法利用先验信息缓解FBP重建对投影数据的依赖性．Golyandina等[11]研究了自回归过程中自协方差矩阵的逆与C成正比情况下的矩阵反卷积问题，证明了这类矩阵的反卷积在Hankel结构低秩逼近问题中的重要性．

以上各类复原算法，多是基于单独去除噪声和单独数据不完备的情况下考虑的，为了进一步降低CT的X光射线计量，在同时降低投影视角和降低管电流强度的情况下，本文将改进帝王蝶(RNAMBO)算法与稀疏贝叶斯(SBL)相结合，引入图像盲复原过程中，提出一种基于稀疏贝叶斯学习-改进帝王蝶算法的盲复原方法．基于贝叶斯框架的CT图像盲复原的关键问题在于建立精确的先验分布模型，包括稀疏系数、点扩散函数、模型参数等，建立联合分布模型，从众多解中找出最优近似解，解决盲复原的欠定问题．稀疏贝叶斯算法中超参数采用最大似然法进行估计，根据其易陷入局部极值的缺陷，本文提出采用帝王蝶算法，并将其改进为RNAMBO算法，用于优化稀疏贝叶斯的超参数，从而建立优化后的稀疏贝叶斯模型，利用大量全剂量CT图像作为先验进行学习训练，抵消字典学习类算法会将伪影及分割边缘误认为有效信息的问题，加快收敛速度．在图像重建中，考虑并消除了点扩散函数的影响．采用压缩感知对CT图像进行稀疏表示，在仿真模型及临床CT图像上进行实验，并与其他研究算法进行比较，通过对比实验，实现了更有效的低剂量CT图像盲复原重建，此算法保留了更多的纹理细节，在投影数据质量严重降低后，依然拥有良好的重建效果．

1 稀疏贝叶斯-改进帝王蝶算法模型的建立

1.1 稀疏贝叶斯算法原理

Tipping[12]提出了相关向量机(RVM)的算法模型．Daniel[13]提出了一种基于信息向量机的稀疏表示方法，还包括一些额外的修改，以保证更好地逼近后验分布．Jiang等[14]基于给定观测模糊图像的情况下，使潜在图像和核的概率最大化的优化原则，提出了一种基于动态规划的方法来近似计算与所提出的正则化的相关算子，得到了更好的盲复原图像．Siwar等[15]基于一个层次贝叶斯模型，使用复杂的Bernoulli-Laplace混合模型来提高目标图像的稀疏度，提出新的贝叶斯正则化算法，与现有的正则化方法相比，稀疏贝叶斯方法具有更好的性能．Zhang等[16]将CT图像采用贝叶斯的稀疏表示，提出了一种离线字典稀疏的迭代重建算法，可以更好地恢复CT图像中的纹理细节，保留医学图像的病理特性．

首先采用压缩感知方法对CT图像进行稀疏表示，假设有数据集成像模型的向量形式表示为

式中：P为含噪声的CT投影数据；A为CT下采样扫描系统矩阵；H为退化矩阵，由点扩散函数h组成；待重建的CT图像为q=Ψα[17]，Ψ为稀疏变换矩阵，α为稀疏变换系数矩阵，稀疏系数包含了最大数量的必要信息；e为噪声矩阵．基于贝叶斯压缩感知的低剂量医学CT图像盲复原重建的目标是根据含噪声的投影数据和参数的先验分布估计稀疏系数和退化矩阵，采用不同的先验模型来描述稀疏系数矩阵α和点扩散函数h．利用稀疏贝叶斯模型建立投影矩阵与其他参数的概率模型．

假设稀疏贝叶斯的训练样本满足独立分布，则其训练样本集的似然函数为

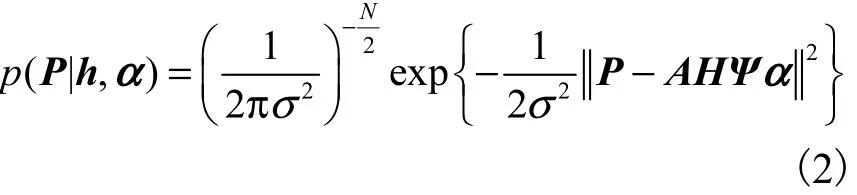
式中：2σ为噪声的方差；N为噪声投影的数量．学习训练的目的是为了估计h值，点扩散函数的估计值将直接影响图像的盲复原效果，根据稀疏贝叶斯理论，h的概率分布限制在0周围的标准正态分布，可以降低模型的计算复杂度．由贝叶斯理论可知，若有已知模型参数的先验概率分布则未知数据的后验概率分布为

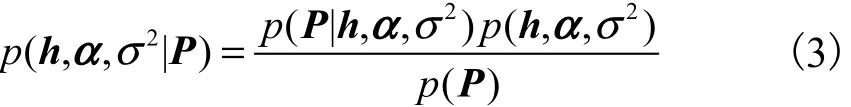
假设用全剂量CT作为测试集的先验数据*x，对相关的投影*P进行预测，则假设h的后验概率分布为

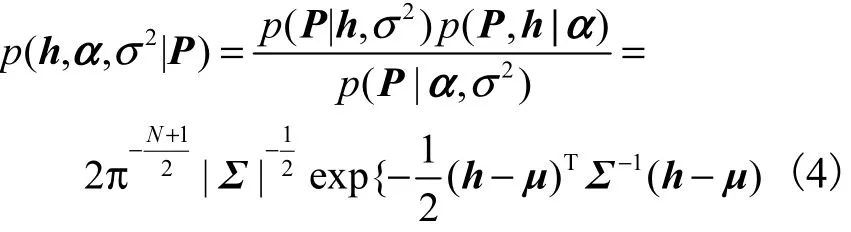
式中：µ为正定矩阵；Σ为协方差矩阵；α和2σ的后验分布可以认为是近似狄拉克分布为α的极大似然估计的极大似然估计．基于上述推导，可以计算预测值*P的分布为

1.2 RNAMBO算法

群智能优化算法作为随机算法的一个重要组成部分，已展示出解决复杂多维度优化问题的高效能力[18]．源于自然界的元启发式算法具有强大有效的处理高维度非线性问题的性能[19-20]．Wang等[21]提出了帝王蝶优化算法，本文采用改进的RNAMBO算法来优化稀疏贝叶斯学习的超参数．

RNA遗传算法包括换位、颈环、置换操作．MBO原始算法中会对帝王蝶进行排序，从最优到最差，利用这一操作，筛选出种群中位置最好的1/4进行保留．下面对最好位置的1/4帝王蝶进行RNA的换位、颈环变换，将种群恢复至原来的1/2．将1/2的帝王蝶种群进行RNA置换操作，将现有种群数恢复至原始种群数，得到新的帝王蝶位置信息，再将更新得到的更好位置信息遗传给子代．通过这一改进，可以在一开始就淘汰掉位置不佳的帝王蝶，对最好的1/4种群引入RNA算子，达到进一步的种群优化的目的，从而大大提升原有MBO算法跳出局部最优的能力，并且可以增加搜索范围，增加MBO动态种群变化，最终达到快速收敛目的．

为降低RNAMBO算法的复杂度，以概率sP执行一部分RNA序列的换位操作，对另一部分RNA序列以概率执行颈环操作，以此优化原始帝王蝶的种群结构，提高RNAMBO算法的迭代效率；然后将全部RNA链以概率进行置换操作，提高了RNAMBO种群的多样性，加大扰动力度，使算法可以跳出局部最优．经过实验RNA 3种操作中pnew对算法性能影响最大，在前期迭代种群多样性尚佳时，为了使算法达到最快收敛，pnew应该较小，随着帝王蝶种群的迭代进化，种群多样性会降低，为了避免算法无法跳出局部最优，应加大扰动力度，pnew应该较大，因此提出一个新的RNA自适应置换概率，可表示为

式中：p为算法初始阶段置换概率；φ为算法置换概率变化范围；Gmax为算法的最大更新代数；g为算法当前的更新代数；BAR为调整率．

式(2)更新为

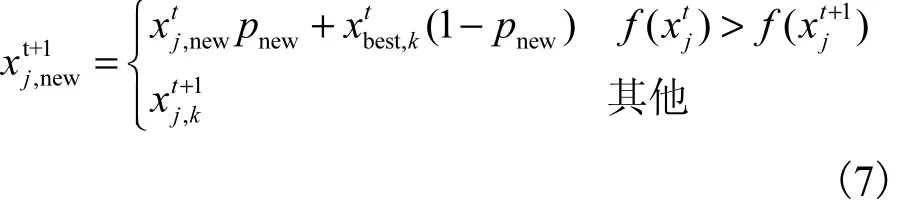
PSO类算法在图像复原及配准中应用较多，但此类算法通常需要1000～5000次迭代，并且粒子自身维度需要保持5～10倍以上，才能有足够搜索能力．因此每次迭代计价过大[22]．改进帝王蝶算法可以同时更新交叉算子和调整算子，所以更适合解决复杂的并行问题，尤其在双模和多模寻优上，比遗传算法[23]、萤火虫算法[24]、PSO[25]等算法更适合解决并行问题及高计算复杂度问题．

2 SBL-RNAMBO算法CT盲复原方法

2.1 SBL-RNAMBO算法实现流程

根据贝叶斯准则，求解带重建CT图像q的最大后验估计为

式中：β为惩罚参数；iR(q)为CT图像先验信息的惩罚项．建立低信噪比少视角投影数据的统计迭代重建最小化目标函数为

Ω为正则化参数，将r设为权重值，随算法的迭代次数自动减小，以减小点扩散函数对重建图像的影响，RNAMBO自适应置换概率可以满足此条件．更新后的迭代公式为

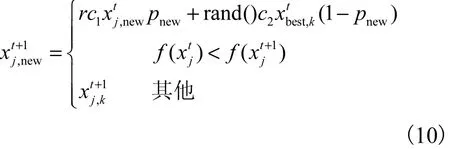
式中：rand()取[0，1]之间的随机数；c1、c2为学习因子，通常取值为2；r为权重因子，代表点扩散函数的权重．实验中的种群初始化参数设置如表1所示．其中M为种群数量，D为维数，i termax为最大迭代次数.

表1 RNAMBO参数设定Tab.1 RNAMBO parameter setting

2.2 SBL-RNAMBO算法的实现步骤

SBL-RNAMBO的算法流程如图1所示．

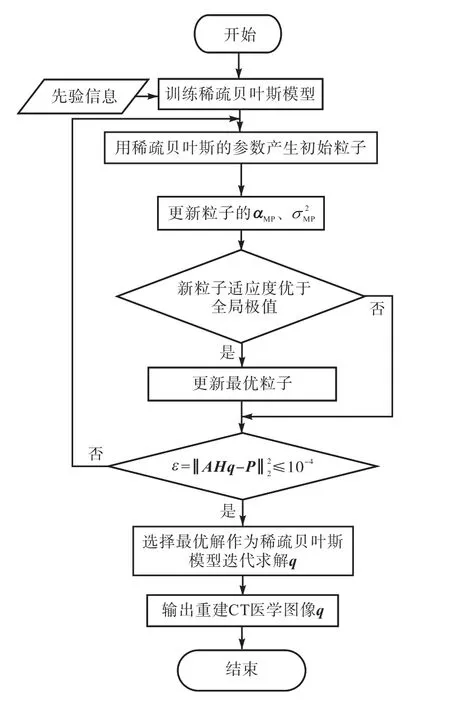
图1 SBL-RNAMBO算法流程Fig.1 Flow chart of the SBL-RNAMBO algorithm

步骤1初始化RNAMBO种群确定种群数量M，给定算法权重因子h的上限和下限值，设定算法的最大迭代次数 itermax，给定的初始解为

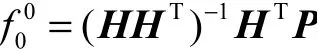
步骤2在的邻域随机生成初始种群，以保证RNAMBO算法的搜索能力，避免过早陷入全局最优．根据式(10)将每个粒子的个体初始位置设置为当前位置．

步骤3根据式(9)得到适应度函数

利用得到的稀疏系数矩阵α，更新重建图像q；λ为权重因子矩阵．

步骤4按照式(6)、式(10)依次计算并进行迭代，更新种群中帝王蝶个体的自适应度值，计算当前迭代个体最优解和帝王蝶种群最优解分别为

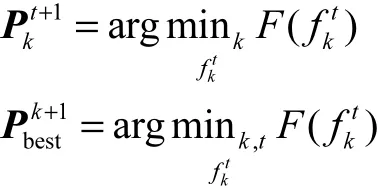
步骤5将每个帝王蝶的自适应度与上一代粒子比较，若优于上一代则进行替换．此时对应的增广拉格朗日函数[26-27]为

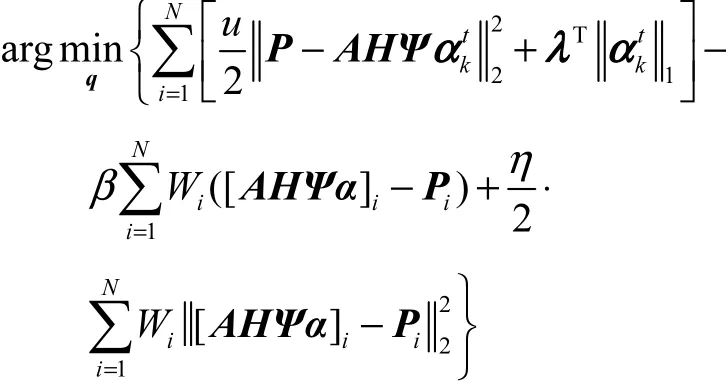
式中：u取 26；η取210；W为统计加权系数矩阵；β为增广拉格朗日算子，且有

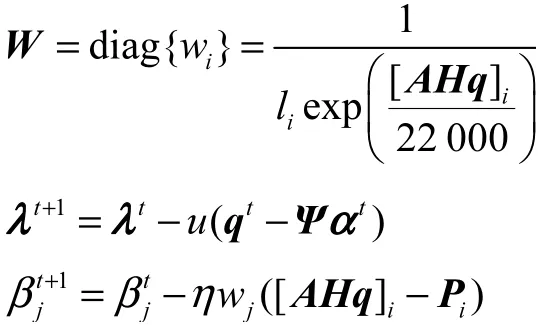
步骤6验证是否满足迭代停止条件：终止目标为或迭代到达最大迭代次数，否则返回步骤3，输出重建CT图像q．

3 SBL-RNAMBO盲复原方法实验结果及分析

本文分别采用Shepp-Logan模型、真实人体盆腔CT扫描图像、真实人体头部CT扫描图像进行对比实验，全剂量图像如图2所示，图像大小为512像素×512像素．采用文献[28]相同参数模拟低管电流20mA扫描时的扫描剂量．系统噪声矩阵e选用混合高斯模型[17]．在同样的测试条件下，选取3种低剂量CT复原算法与SBL-RNAMBO算法应用于低剂量CT图像的重建算法进行实验对比：FBP＋BIR[17]算法、VVBP-FBP重建算法[10]、高斯混合MRF迭代重建算法(G-MRF)[29]、盲源分离、块滤波算法(MBSS)[30]和字典学习(DL)算法[31]．下面通过具体实验数据进行分析.

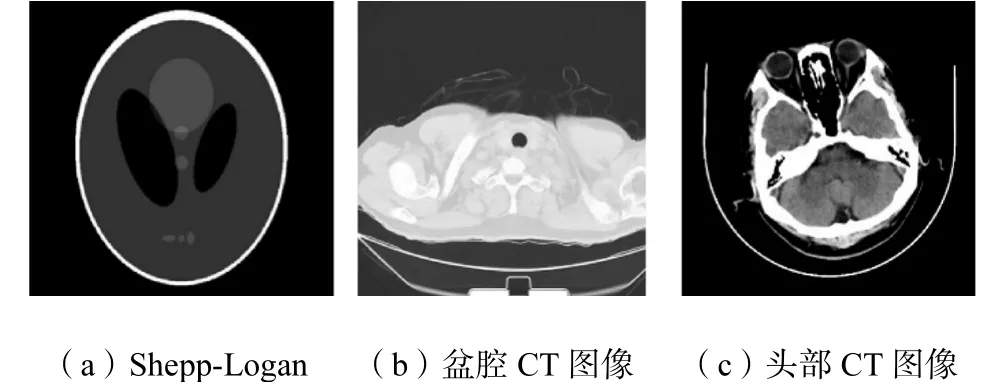
图2 512×512 CT扫描图像Fig.2 Image of CT scanning(512×512)

3.1 Shepp-Logan模型实验结果分析

实验采用扇形光束扫描方式，完备投影数目下旋转角在 360°范围内均匀采样值为984，每个角度下的探测器数为888．为了验证SBL-RNAMBO算法的效果，在360°圆周内均匀选取145和90个扫描视角数，如图3和图4所示，分别为20mA、145个投影数目和20mA、90个投影数目的实验对比(所有实验数据均为同等实验条件下，取10次实验的平均值)．

如图3所示，当扫描视角数目降到145个时，X射线的扫描视角数目已不足全剂量CT扫描视角数的15%，可以看出FBP＋BIR算法伪影严重并伴有大量噪声，因为FBP＋BIR重建算法对数据的完备性要求很高，一旦投影数目少于重建所需数目，FBP＋BIR算法的斜坡滤波器将不能有效地滤除非平稳高斯噪声，受投影数据不完备和高噪声的双重影响，在此条件下重建效果很差；基于VVBP的重建算法利用奇异值分解进行图像处理，复原效果优于FBP＋BIR算法；G-MRF算法利用混合高斯进行二次优化，相比MBSS算法，Shepp-Logan图像的重建效果稍好，但该算法不能完全消除噪声的影响，因此，图像中存在由噪声引起的伪影；MBSS算法是以非局部块匹配为准则的迭代重建算法，由于数据不完备而造成的粗条纹伪影有所降低，但在图像中存在噪声引起的细条纹伪影．DL算法利用字典学习进行学习，可以得到较好复原效果，但块内信息处理能力不足，细节保持稍差．SBL-RNAMBO重建算法中使用的先验信息是从多幅全剂量CT图像训练得到的，对于恢复纹理结构特征更有针对性，算法中优化后的超参数可以得到更好的对点扩散函数估计，并且增强了抗噪性能，成像效果最佳．

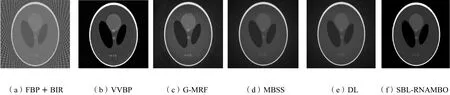
图3 20mA、145个投影数目下Shepp-Logan复原对比Fig.3 Comparison of the Shepp-Logan restoration under 20mA and 145 projections

如图4中所示，当扫描视角数目降到90个时，X射线的扫描视角数目已不足全剂量CT扫描视角数的10%．此时投影数据完备性更差，且降低管电流会伴随大量量子噪声，FBP＋BIR、VVBP-FBP＋BIR算法的复原效果比145个扫描视角时更差，复原效果更加模糊，边界不清，本文提出的SBL-RNAMBO算法的复原图像仍然比较清晰，伪影几乎被抑制，复原效果较好．

为了定量分析本文采用4种评价指标对实验结果进行分析和对比，分别是峰值信噪比(PSNR)、通用图像质量指数(UIQI)、结构相似性指数(SSIM)、误差方差和(SSDE)[17]和运行时间，如表1所示．

从表2中可以看出，在投影数据进一步恶化的实验条件下，本节提出的两种方法在SSDE、UIQI、PSNR、运行时间的指标上均明显好于对比算法，尤其在PSNR上提升明显，运行速度也大幅降低，这是由于使用RNAMBO优化超参数后加速了算法收敛速度，使稀疏贝叶斯学习训练时间缩短，系统误差方差和降低，SSIM指标上有一定的提升．

图4 20mA、90个投影数目下Shepp-Logan复原对比Fig.4 Comparison of the Shepp-Logan restoration under 20mA and 90 projections

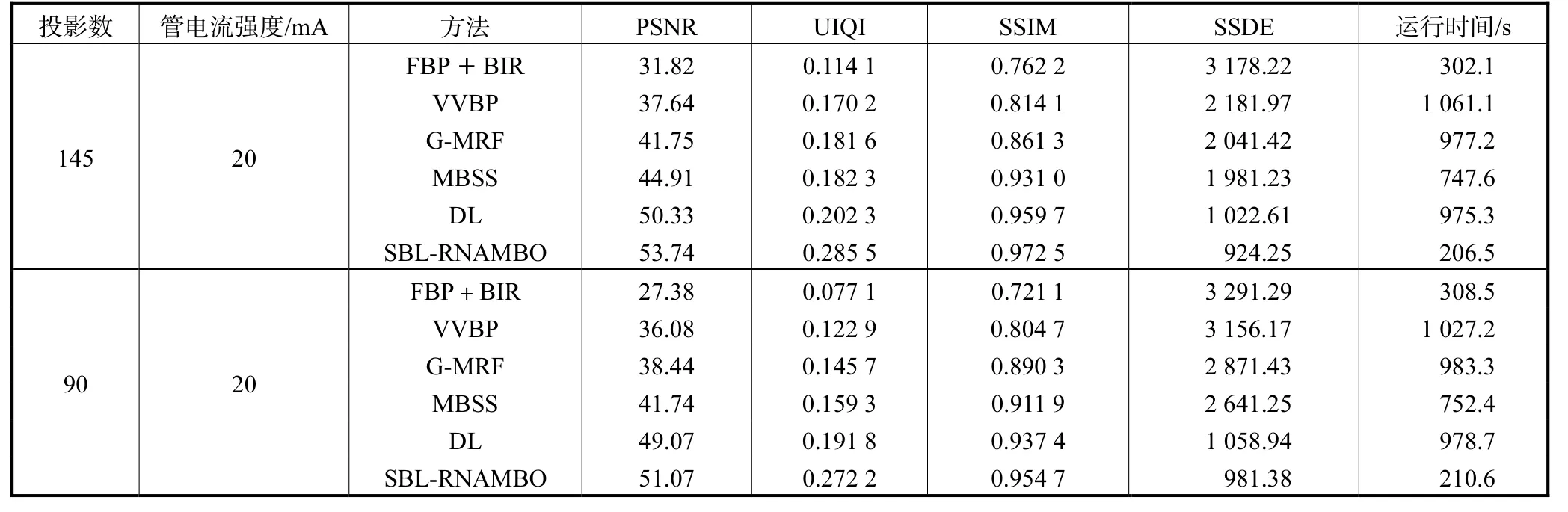
表2 Shepp-Logan定量指标对比Tab.2 Comparison of the quantitative indices of Shepp-Logan

3.2 临床实验结果分析

3.2.1 盆腔CT图像盲复原实验

本文将盆腔、头部各取5名真实病例的全剂量真实医学CT图像(图像来源：天津信泰医院及天津血研所)作为先验信息，进行稀疏贝叶斯学习．盆腔CT图像来自GE Hi-Speed多层CT设备扫描，显示窗为[－500HU，900HU]．在20mA、145个投影视角条件下的实验结果如图5所示(所有实验数据均为同等实验条件下，取10次实验的平均值)．

FBP＋BIR算法很容易受到噪声的影响，尤其是在低信噪比条件下，算法性能迅速恶化．VVBP相比FBP＋BIR重建算法虽具有较好的性能，但是在重建中会有严重的伪影投射，并且丢失大量纹理细节；GMRF算法在使用盲复原的情况下会导致过度平滑丢失纹理细节；MBSS算法的块匹配机制在噪声严重的情况下会将伪影误认为有效信息，使得重建效果变差；DL算法在处理块内结构时取平均，会误将伪影当作有效信息进行保留；本文所提出的算法削弱了点扩散函数对重建图像的影响，针对低信噪比低管电流强度的情况，提高了重建图像的质量，可以在连续优化的基础上进行迭代．当投影数目降低到90个时，如图6所示，为了看清复原细节，将感兴趣区域放大，可以看到SBL-RNAMBO算法能有效地抑制噪声并保持图像纹理细节，在图像重建后，拥有最清晰的图像复原效果．从表3的数据中可以更明确地看出在4种定量指标对比下，本文提出的算法在PSNR值上有较大提升，VVBP算法、G-MRF算法、MBSS算法及DL算法的UIQI值随着投影数目和管电流强度的降低下降较为明显，但本文提出的算法还保持着较高的UIQI值，在SSDE指标上SBL-RNAMBO算法的改善也较为明显，这说明算法有较小的误差，运行时间上，因为RNAMBO可以帮助算法更快地收敛，大大缩减了运算所需时间，本文提出的算法在所有定量指标对比上均优于其他算法，尤其是SSDE和UIQI的改进较为明显．

图5 20mA、145个投影数目下盆腔CT复原对比Fig.5 Comparison of the pelvic CT restoration under 20mA and 145 projections

图6 20mA、90个投影数目下盆腔CT ROI对比Fig.6 Comparison of the pelvic CT ROI under 20mA and 90 projections

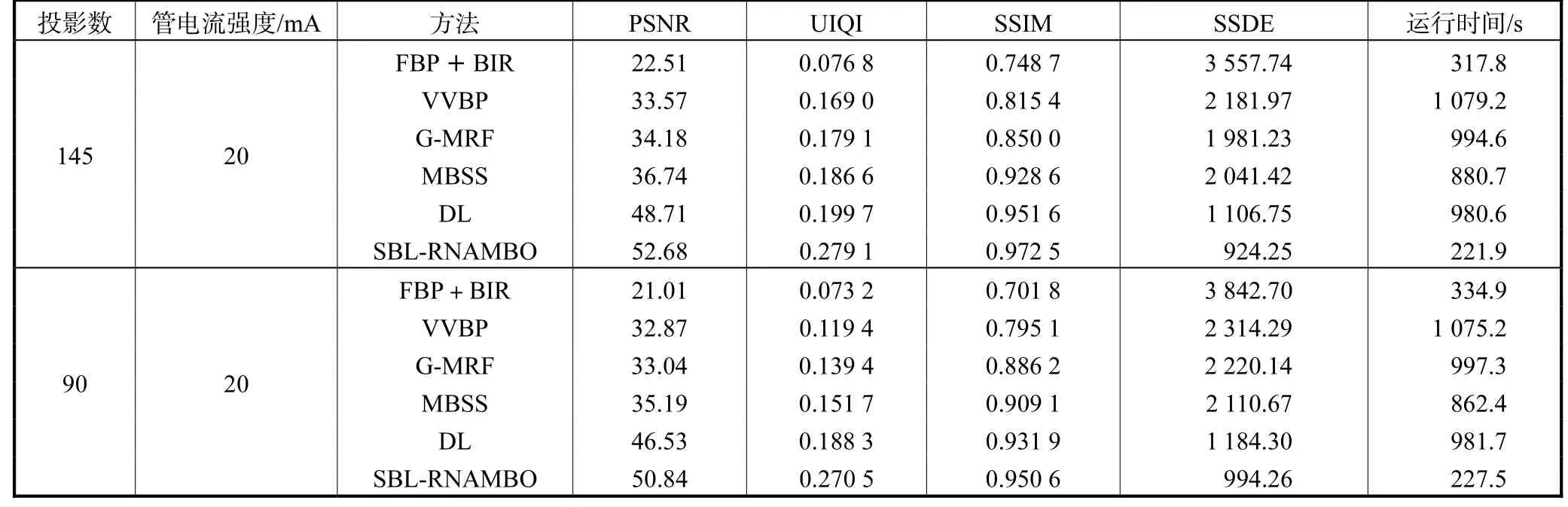
表3 盆腔CT定量指标对比Tab.3 Comparison of the quantitative indices of pelvic CT

3.2.2 头部CT图像盲复原实验

头部CT图像来自GE Hi-Speed多层CT设备扫描，共32层，层厚10mm，选取其中一层，显示窗为[80HU，100HU]．头部相对于盆腔，会有更多的纹理细节及局部特征，在20mA、145个投影视角条件下的实验结果如图7所示，可以观察到VVBP算法的边缘出现了轮廓不清的情况，脑部构造细节过于平滑并伴随伪影．G-MRF算法、MBSS算法及DL算法在边缘处出现了脑部纹理构造模糊的情况，有少量条纹状伪影，脑部的细节也有所丢失．SBL-RNAMBO算法在细节保持及纹理恢复方面较为突出，基底动脉、小脑半球、脑桥等细节部分得以清晰保留，并且没有伪影干扰，图像的信息得到了较好的复原．将感兴趣区域放大如图8所示SBL-RNAMBO算法的复原效果相对较好，放大后依然可以看到小脑蚯部和四脑室的细节，图像边缘恢复比较理想．综合比较，本文提出的算法在放大后的复原效果都比其他对比算法更清晰，保留了更多的诊断所需纹理细节．

从表4的数据中可以更明确地看出，在低管电流条件下，随着投影数目降低，在SSDE指标的对比中，SBL-RNAMBO算法保持了较低的均方误差和.在SSIM和PSNR指标的对比中，SBL-RNAMBO算法的改进效果最为突出．UIQI指标的对比中，SBL-RNAMBO算法的优化效果比对比算法高出近1倍，具有良好的重建性能和数据指标，运行时间也 最快．

图7 20mA、145个投影数目下头部CT复原对比Fig.7 Comparison of the head CT restoration under 20mA and 145 projections

图8 20mA、90个投影数目下头部CT ROI对比Fig.8 Comparison of the head CT ROI under 20mA and 90 projections

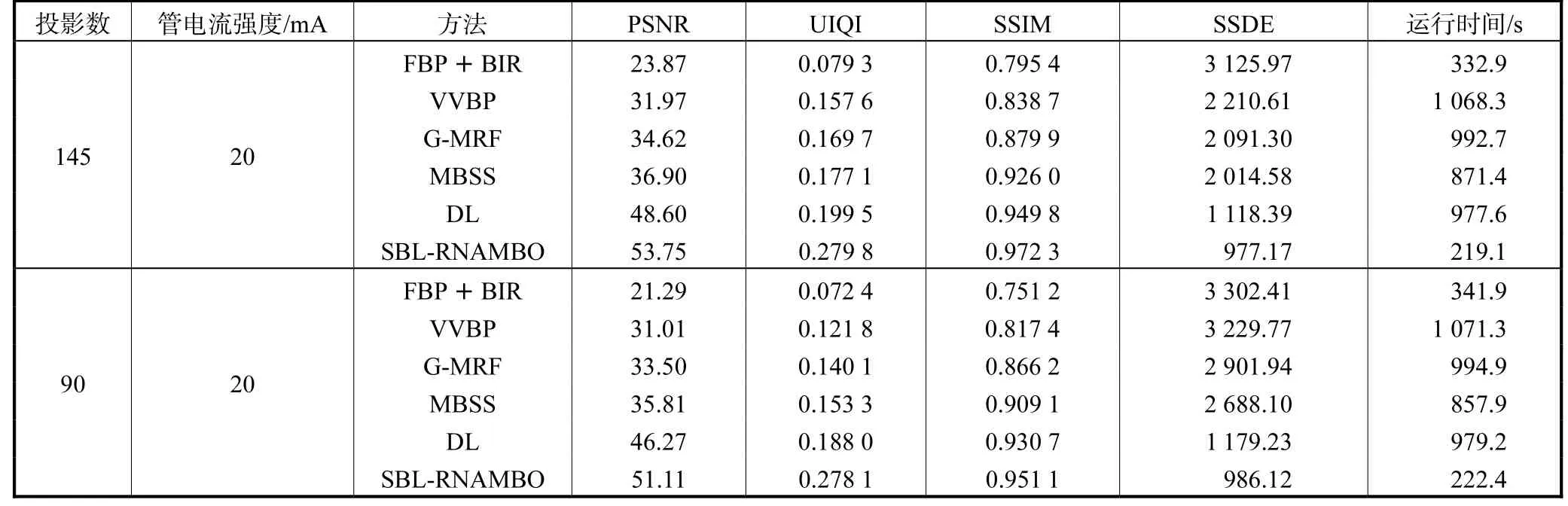
表4 头部CT定量指标对比Tab.4 Comparison of the quantitative indices of head CT

3.3 SBL-RNAMBO算法稳定性实验分析

为了验证算法在不同初始值下的性能，给定噪声方差均值为0的高斯白噪声，2σ分别为10、15、20、25的条件下，对不同的图像进行峰值信噪比实验．并给出不同RNAMBO初始参数设置条件下的实验结果对比，如表5所示，实验结果为独立运行30次的平均值．可以看出不同2σ初始值下，SBL-RNAMBO算法均可获得较高的峰值信噪比．

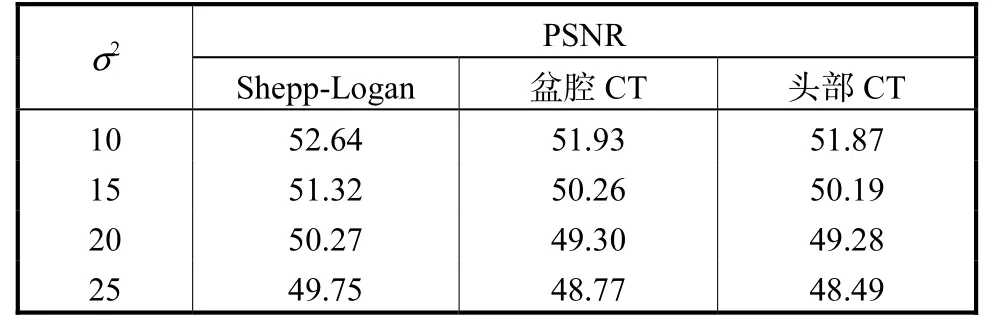
表5 90个投影数20mA管电流强度下不同初始值PSNR指标对比Tab.5 Comparison of PSNR indices with different initial values of 90 projections at 20mA tube current intensity

4 结 语

本文提出了一种基于稀疏贝叶斯学习-改进帝王蝶的低剂量CT图像盲复原算法，用RNAMBO算法优化超参数，将盲复原低剂量CT图像转化为求解最优化的问题，基于盲复原的欠定性，选用统计迭代算法进行重建，加入惩罚项约束解空间，结合智能优化加快算法收敛速度，提高图像复原质量．实验表明建立的SBL-RNAMBO模型能够实现连续迭代优化，图像保留了图像边缘和诊断所需的生理细节，视觉效果上明显优于其他算法．

该算法考虑并消除了点扩散函数的影响，求出盲复原欠定问题的最优近似解．临床实验结果显示SBL-RNAMBO算法优于其他对比算法，在数据不完备且管电流降低造成噪声干扰的情况下，可以重构出高质量的图像．同时，在定量指标评价方面，该算法对PSNR、SSIM、UIQI、SSDE、运行时间指标均有较大改进．将大量真实的病例信息作为图像的先验信息，增强了算法的可靠性及准确性，提高了算法的性能．未来将在RNAMBO与医学配准方向进行进一步的研究与实验．