埋头弹中超高速弹丸的多区间电磁检测方法

杨伟鸿，陈立，刘毅，马强平，韦云清，李兴文

(1.西安交通大学 电气工程学院，陕西 西安 710049；2.中国兵器工业西安近代化学研究所，陕西 西安 710065)

作为一种新型弹药，埋头弹在保持较低成本的同时总体性能比常规弹药提高了30%，不易损坏，引起了广泛关注[1]。虽然研究者对点火结构已经开展了相关研究，但对埋头弹的初始燃烧特性的认识不足，缺乏相应的模拟试验装置以研究埋头弹的一级点火和冲击挤进过程的特性。在点火过程中，冲击挤进过程对火炮的整体性能起着决定性的作用[2]。弹丸在冲击挤进过程中的运动特性可以直接反映埋头弹的设计、其附属装置在实际点火过程中的性能和武器特性。因此，通过对弹丸运动特性的精确评估，可以实现埋头弹及其弹道支撑装置的优化设计[3-6]。

目前埋头弹及其弹道支撑装置的设计过程很少涉及对一级点火和冲击挤进过程中弹丸运动特性的评估，而只对一些后膛线动力学参数进行分析，如弹丸出膛速度、最远射程等[7-11]。另一方面，随着新型推进剂研究的不断深入，对埋头弹点火过程的研究显得尤为重要，但在点火方案设计方面的相关研究较少。对于弹丸出膛速度的分析，最常用的方法是高速摄影法[12-13]和多普勒雷达法[12]。高速摄影法计算弹丸的速度虽然很简单，但对周围环境的要求很高，只能在高光强度及高清晰度下测量。对于一级点火过程和冲击挤进过程，弹丸的运动区域是从埋头弹弹壳到枪管的非透明区域，采用高速摄影方法是不可行的。多普勒雷达法测量精度高，可用于多种类型的弹丸速度测量。但由于其体积大、运输不便、价格昂贵，只能在某些特定场合使用。同样，在弹丸撞击挤进过程中，多普勒雷达装置发出的电磁波无法进入埋头弹腔内，因此不能对弹丸进行实时检测。所以，迫切需要一种高效、准确的检测方法。

针对现有方法在不透明结构中无法实时测速的缺点，提出了一种基于电磁感应规律的多间隔测量方法，其优点是即使在非透明的半封闭结构中，也能实现弹丸速度的实时测量。在埋头弹腔体外面轴向方向放置一系列具有特定间隔的感应线圈，以获得高速运动的磁化材料在感应线圈上产生的感应电动势信号；利用这些电动势信号，以曲线簇的过零点为时间点，采用多间隔测量法求解埋头弹弹丸的实时速度。此外，还考虑了影响测量精度和灵敏度的因素，如涡流效应和磁铁偏移，最后给出了长度测量误差和时间测量误差的综合不确定度。

由于一级点火的压力和温度没有破坏性，因此可以利用高强度的非铁磁曲面做模拟装置来研究冲击挤进过程的机理。

1 原理及测量方法

目前已经研究提出了多种测量方法。然而，它们大多受到“高分辨率要求”“不透明结构”或“快速反应”的限制。由于埋头弹的半封闭结构，在设计测量设备时应考虑以下问题：采用非接触式测量方法，以避免运动弹丸的干扰；为了实现对弹丸在冲击挤进过程中运动速度的实时监测，测试设备应具有响应快、干扰小的特点；由于埋头弹的外壳由金属制成，因此应特别考虑涡流效应和磁饱和现象，以及测试设备中使用的电磁波的穿透能力[14]。

弹丸具有磁性，其运动会引起磁场变化，因此提出了一种基于电磁感应定律的磁线圈法[15]。测量装置的装配图如图1所示。埋头弹的外壳是由非磁性金属(铜或丙烯酸板)制成的，同时，弹丸使用顺磁性材料制成，从而可以被镶嵌在弹丸末端的钕铁硼磁体(Nd-Fe-B磁铁)磁化。利用MAXWELL软件对弹丸运动和弹道特性进行评估，并对弹丸在一级点火和冲击挤进过程中的速度进行了计算。

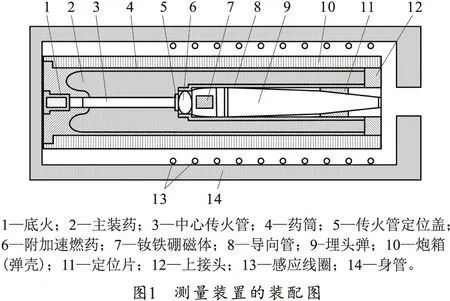
由于运动物体的半径远小于感应线圈的半径，而且物体的长度也小于线圈的半径，为了便于分析，根据感应线圈的基本原理，将磁化后的高速运动物体视为磁偶极子，其特性可以用磁矩来描述。在仿真模型中，磁矩的方向与弹丸运动的方向和线圈轴线的方向一致。因此，对线圈的分析可以转化为对磁偶极子通过半径为R、匝数为N的线圈所产生的感应电动势的分析[16]。开始时，一旦触发底火，随即点燃附加速燃药，并施加初始推力将弹丸推进至坡膛，如图1所示。在冲击挤进过程中，通过与线圈组连接的示波器可以获得一系列感应电动势的时变信号。

通过单个感应线圈的磁通量Φ为

(1)

式中：z是磁偶极子在坐标系中的位置；B为磁密；S为线圈在磁力线方向的投影；μ是相对磁导率；p为磁偶极子；R是感应线圈的半径；c是抛射体与感应线圈轴线的偏移；φ是线圈平面方位角。

由于z=z(t)，即可得到磁通量随时间变化的表达式。若c=0，即表示在弹丸和线圈的轴线之间没有偏移，则式(1)被简化为

Φ(t)=μpR2/[2(R2+z2(t))3/2].

(2)

式(1)的计算几何图解如图2所示。

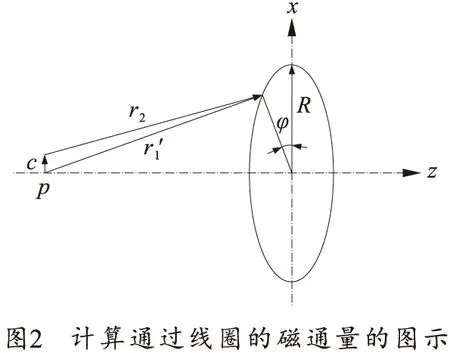
当速度为v的磁化运动弹丸通过感应线圈时，线圈中感应电动势可以表示为

(3)

考虑涡流的影响，将壳体中的电流等效为一个与感应线圈一样工作的“等效线圈”，并利用其磁场作为附加磁场，从幅值和方向上修正原始磁场。

在仿真时，利用有限元法的思想迭代求解埋头弹各点的磁场分布，并利用壳体的涡流效应对原始磁场进行修正。当弹丸向前推进时，感应线圈中会产生一系列电动势。由于磁矩的方向，即线圈轴线方向的磁通密度方向不改变，磁通密度的大小经历了从小变大、然后再变小的过程，所以系列电动势存在过零点。

由于涡流效应，埋头弹壳体内存在一个附加磁场，该附加磁场滞后于钕铁硼磁体产生的原始磁场。图3所示为壳体的结构网格，其尺寸相当于导电线圈的横截面积，由此可以等效为一组附加线圈。根据式(3)可以计算出电动势，考虑到磁饱和和集肤效应，壳体内的电流强度可以计算如下：

J=μE,

(4)

式中，μ是通过二维插值计算的磁导率，是磁场强度和温度的函数。因此，可以很容易地获得附加磁场，以修正原始磁场的分布，并提供更精确的弹丸速度检测。

如上所述，可以将壳体看作是一组附加线圈(图3中的黑色正方形)，以便在减少计算量的同时校正原始磁场。用于计算埋头弹外壳中涡流激发附加磁场分布的网格划分示意图如图3所示。

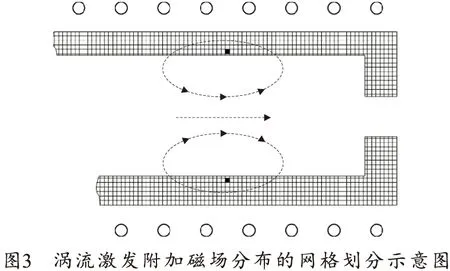
计算涡流效应的过程如下：

1)将计算域中的埋头弹壳细分为网格；

2)计算磁感应强度在计算域内的分布，进而计算感应线圈中的电动势；

3)根据欧姆定律，可以得到壳体中的电流密度，从而计算出“附加线圈”中的电流；

4)以“附加线圈”中电流产生的附加磁场作为校正量，对钕铁硼磁体产生的原始磁场进行校正；

5)重复第2步进行迭代计算，直到计算区域满足磁场的高斯方程。

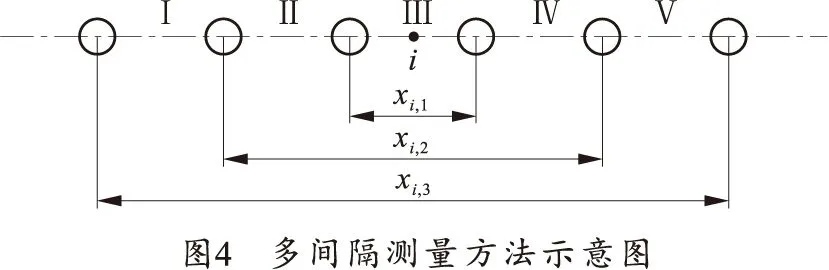
由此得到一系列过零点。采用多区间测量法求解各位置的速度[17]。各段平均速度计算如下：

(5)

式中,Δxi,j为特定截面第i个中心点计算间距的第j个长度。

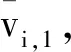
(6)

式中：vi是弹丸在位置i处的速度；∑j是多间隔方法中使用的间隔数。事实上，不同间隔之间的距离越大，速度差越大，因此，在多间隔测量方法中使用的最大间隔数不大于3.

2 计算结果与分析

为了验证仿真模型的可行性，对弹丸的运动过程进行了如下设定：弹丸从静止匀加速到70 m/s；忽略摩擦力；速度曲线是由计算得到的速度数据线性拟合而成的。对于仿真测试中不同的情况，分别使用磁体偏移量为2、5和8 mm的弹丸。

在以往的一些低速弹丸运动仿真研究中，将弹丸的运动速度定为一个常数，例如70 m/s，就可以使装置产生可检测的感应电动势。但是对于一个加速运动，要用以前的研究方法在运动的初始阶段检测到如此小的电动势是不可行的。

2.1 涡流的影响

由于涡流会阻碍磁场的变化，有涡流效应的情况下磁感应强度的变化率小于无涡流效应的情况，如图5(a)所示。有涡流效应的情况下电动势的变化率小于无涡流效应的情况，没有涡流效应的情况下，磁感应强度的大小变化比有涡流效应的情况更快更大，说明dB/dt存在差异，这也是红色曲线簇代表涡流效应的最大值小于蓝色曲线簇最大值的原因，尤其是在其负半轴，如图5(b)所示。此外，无涡流效应的电动势曲线簇略高于有涡流效应的情况，因此，在没有涡流影响的情况下，计算出的速度将略大于预设值，并且在预设曲线之前，如图5(c)所示。

2.2 与已有研究的比较

Keiko Watanabe等人开展了一种利用电磁线圈进行高速穿透的研究[14]，使用了高达900 m/s的速度。为了验证仿真模型的可行性，将仿真模型的结果与Keiko的工作进行了比较，如图6所示。因为弹丸在穿透箱形沙土时会减速，仿真中采用了类似的阻力系数。

从图6可以看出，仿真结果与Keiko Watanabe的实验结果非常接近。但是，由于附近线圈的磁滞效应，仿真计算得到的速度仍略大于实际速度，但只有当速度小于30 m/s时，仿真结果才小于实际速度。随着弹丸速度的降低，磁滞效应对速度的影响更加明显。

2.3 磁铁偏移量的影响

为了便于加工，埋入弹丸末端的物体一般被加工成圆柱体，与其轴线重合，如图7所示。

但是，在实际的加工过程中，误差是不可避免的；另一方面，一旦磁铁出现偏移，它将会更接近感应线圈，在感应线圈所在的平面上产生更大的磁感应强度B.当弹丸以相同的速度通过线圈时，带有磁铁偏移的情况下将会具有一个更大的dB/dt，因此感应线圈中感应电动势会变大，从而提高测试系统的灵敏度。

有钕铁硼磁体的线圈输出电压及电压最大值与偏移量的对比图如图8所示。

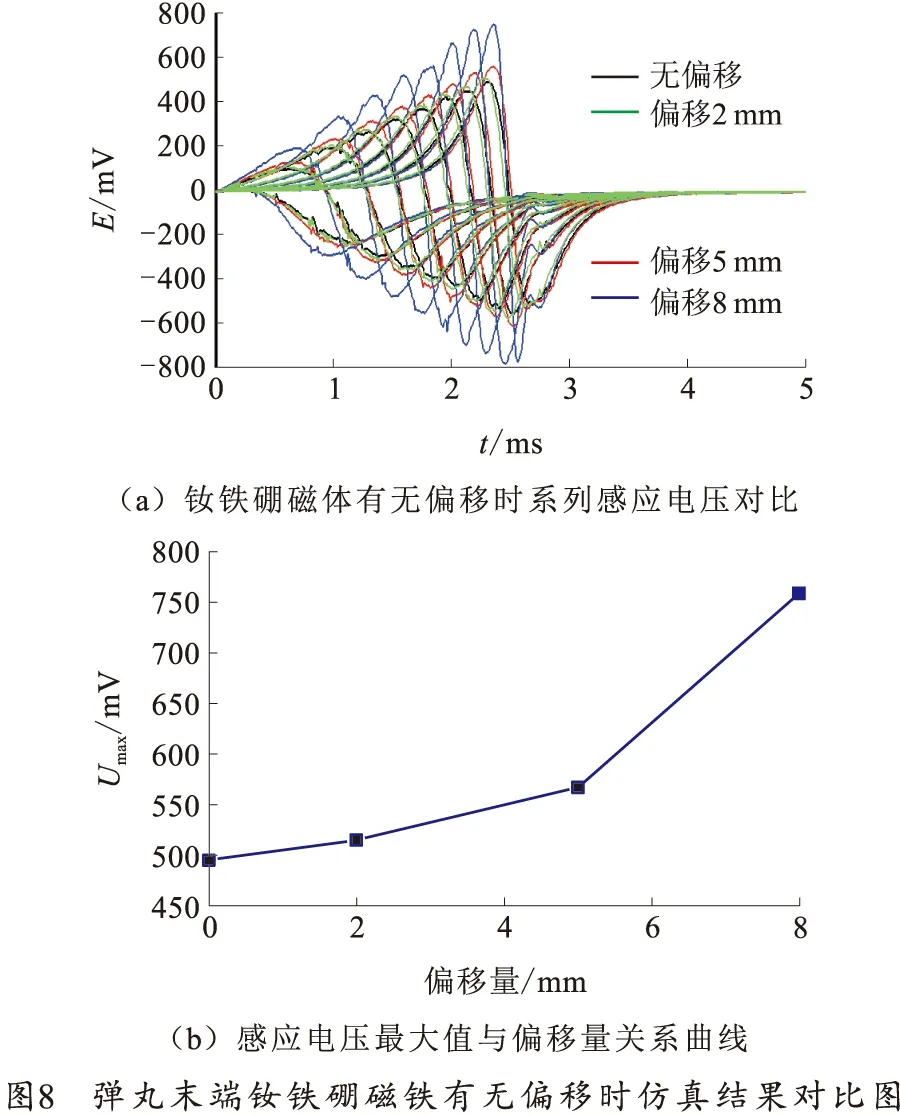
从图8 (a)中可以看出，偏移量为5 mm的情况下，感应电动势的幅值最大为70 mV，偏移量为8 mm的情况下，感应电动势的幅值最大为300 mV，而过零点几乎没有变化。如图8 (b)所示，随着偏移量的增加，感应电动势的最大值增加。在电动势增大过程中，过零点几乎不变，故测试系统的灵敏度将大大提高。在后续的实验和生产中，可以利用带有磁铁偏移的子弹来提高测试系统的灵敏度，降低精度要求。

然而，磁体在弹体末端的偏移会导致弹体质心的径向偏移，在冲击挤进过程中会引起弹体与腔体之间的抖动和摩擦，造成额外的能量损失和失准，从而可能导致弹壳卡住甚至爆炸。为了消除这种质心失衡，可以采用磁铁的对称布局，如图9所示。

2.4 不确定度分析

由于速度检测是通过测量每个间隔的长度和弹丸通过每个间隔的时间来实现的，因此速度的不确定度是长度测量和时间测量误差的函数。

检测系统的不确定度可以描述为

(7)

式中：L是每个间隔之间的默认长度；ut是时间测量的不确定度，由示波器的工作频率引入；ux是长度测量的不确定度，由测量线圈间距引起的误差ux,1、线圈不平行而引起的随机误差ux,2、非平面线圈引起的误差ux,3、线圈直径不同引起的误差ux,4和线圈平面倾斜引起的误差ux,5所组成。

各误差对综合不确定度的影响如表 1所示，各误差的影响因子由式(7)的偏微分计算。

表1 各误差对综合不确定度的影响

由表 1可知，时间测量的误差对综合不确定度的影响较小，而非平面情况的影响最大，因为磁通量是由线圈平面的面积决定的，而非平面线圈减小了磁感线通过线圈的面积。长度测量不确定度统一由RSM公式计算：

最后得到综合不确定度为0.485 8%.

3 冲击挤进试验

为分析埋头弹一级点火结构及弹丸药筒内滑动冲击挤进特性的关联性，设计了弹丸冲击挤进试验系统，系统各部分连接如图10所示。

实验中仅使用1.5 g黑火药作为底火，点火电源触发信号与数据采集触发信号由同步信号发生器进行同步控制，点火电源触发信号滞后于采集信号10 ms，确保高速相机信号、磁感应线圈输出信号、压力传感器信号可以捕捉到点火开始至弹丸运动制止过程。

对于弹丸的速度，除了使用前述磁感应线圈法(电磁法)测量之外，还采用标准刻度板高速摄像的方法获得，以作为电磁法的速度标定。弹道内弹丸前端放置轻质杆，轻质杆前端安置有信标。高速相机(IX Camera i-SPEED 510，分辨率840×594像素@20,000 fps)入射光路与身管轴线垂直，且垂直于标准刻度板(5 mm×5 mm)。弹丸冲击挤进试验轻质杆高速摄像结果如图11所示。

感应线圈输出信号按前述方法进行处理，高速摄像图像在提取信标位置信息后，计算各时间间隔内的平均速度，得到如图12所示的弹丸冲击挤进过程中的速度曲线。由图12可以看出，弹丸冲击挤进过程可以分为3个阶段：

第1阶段：底火点燃，弹丸自药室内的静止位置开始，加速运动至坡膛位置，接触坡膛后弹丸速度迅速降低。

第2阶段：自弹丸前端接触坡膛开始，至弹丸弹带接触坡膛，这个阶段由于内部压力不断增加，弹丸速度迅速增加。

第3阶段：内部压力持续增加，弹丸做匀加速运动。约18.7 s，弹丸运动受拦截器阻挡，速度迅速下降。弹丸受阻前，峰值运动速度为27.3 m/s.

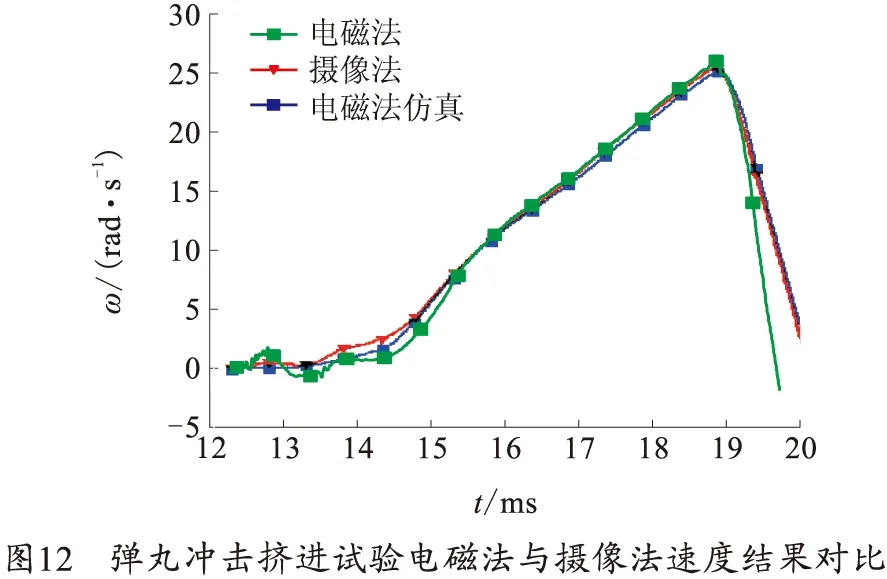
图13中的曲线展示了弹丸冲击挤进过程中弹丸的位移变化，其中摄像法所得位移曲线为拍摄记录位置，电磁法所得位移曲线为其对应的速度曲线对时间的积分。

结合图12、13可以看出，在低速阶段，电磁法测量弹丸运动速度有一定程度的低估，但总体相差不大；另一方面，轻质杆并未与弹丸进行可靠的紧密连接，由于惯性和振动，轻质杆的速度变化略微滞后弹丸的速度变化，且其变化量更小。总体而言，电磁法测量结果与高速摄像法结果吻合度较高。

将图12中高速摄像法测得弹丸运动速度数据作为电磁法仿真模型中弹丸运动的速度，从图中可以看出，在弹丸低速运动阶段，仿真所得速度曲线更为平缓，这是因为仿真模型中引入外壳涡流作用，在低速运动中涡流影响更为突出，致使速度变化略微迟滞、变化幅度更小。当弹丸运动速度提升至约8 m/s后，涡流效应影响效果减弱，仿真结果与摄像法结果吻合度较高，仿真计算所得速度峰值约27.2 m/s.

4 结论

通过MAXWELL仿真，对埋头弹发射过程中弹丸的精确速度进行测量，分析了其弹道特性和高速弹丸通过感应线圈时，涡流效应和磁铁偏移对测量系统输出特性的影响。通过仿真可以得出以下结论：

1)序列磁感应线圈输出的电动势信号幅值受高速运动速度的影响，该系统适用于速度不小于30 m/s的物体的速度测量。在初始阶段，弹丸是缓慢运动通过的，感应电动势过小而无法检测。

2)为减少考虑涡流效应时的计算量，腔体等效为附加线圈。在忽略涡流的情况下，速度测量的仿真结果在数值上有明显的提高，并且与考虑涡流时相比具有明显的时间超前性。

3)磁铁的偏移量越大，信号的幅值越大。当磁铁存在偏移时，磁铁会靠近线圈，磁密增大，单位时间磁场变化率(dB/dt)增大，从而在线圈中产生更大的电动势，而过零点几乎没有变化。然而，另一方面，磁铁的偏移可能导致弹丸轨道运动偏移，这可能造成哑弹甚至炸膛，需对弹丸本身进行配重设计。

4)基于台架测试，开展弹丸冲击挤进试验，分别采用电磁法和高速摄像法对冲击挤进阶段的弹丸速度进行测量。试验结果表明，电磁法测量弹丸在冲击挤进阶段的运动速度，其灵敏度较高，可快速响应弹丸开始运动、弹丸接触坡膛、弹带接触炮管等各个阶段；利用试验中高速摄像法获得的速度曲线作为仿真模型中弹丸的速度预设值，计算结果与预设值(高速摄像法测得的速度)趋势相同，当弹丸速度高于8 m/s，计算结果与预设值吻合度较高，相对误差小于1%.