三维网格去噪算法研究综述

张栋栋，龚伟华

（浙江理工大学信息学院，浙江 杭州 311121）

0 引言

三维网格不仅在动画和游戏制作中十分常见，而且在各种应用如虚拟现实和增强现实、三维模拟、医学形状分析等方面也发挥着至关重要的作用。在三维扫描仪出现之前，三维模型可以由模型设计师通过一些软件如Maya、3Dmax 等创建。如今可以通过扫描仪轻而易举获得现实物体的三维空间数据，但原始网格不可避免地含有噪声，因此网格去噪成为极为重要而有意义的工作。本文梳理和分析了目前学术界的研究进展，总结了已有方法存在的局限性，展望了未来的发展趋势。

1 各向同性网格去噪方法

早期一些经典网格去噪算法都是以各向同性的方式进行的，将噪声与特征都视作高频部分再进行低通滤波处理，这些方法都没有考虑网格自身的特征，如经典的Laplacian 平滑算法［1］不能保持体积，其原理就是将顶点的位置信息用其相邻点的位置信息加权平均来替换，所以在经过多次迭代后会发生收缩现象。

其中N1(i)表示面片i的Ⅰ环邻域。

从图1 的实验结果可以明显看出迭代3 次后有明显的收缩现象，如果无穷次迭代下去最终会收缩成一个圆环［2］。

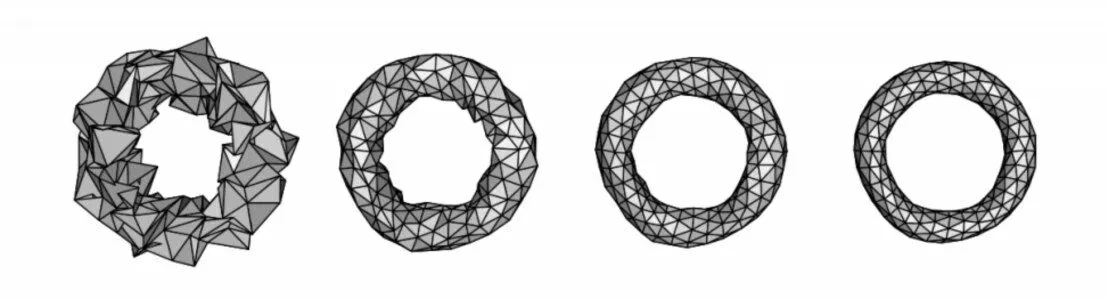
Fig.1 Laplacian algorithm applied to noisy rings图1 Laplacian 算法在有噪声环上的应用

考虑到顶点位置不应该只和临近顶点位置有关，还应该和 顶点初 始位置有关，Vollmer 等［3］提出The HC-Algorithm。在拉普拉斯平滑基础上，目标顶点是对初始位置加权的结果，几何意义上相当于把顶点的位置反向移动一定距离。因为Laplacian 平滑算法平滑过度时HC-Algorithm可以减轻平滑效果，Taubin 等［4］将用于信号处理的一些方法引入Laplacian 算法中，如下所示：

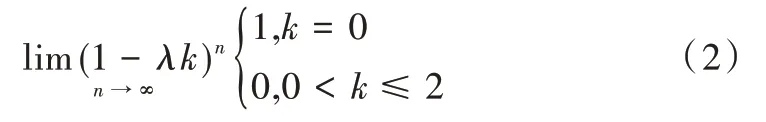
所以，当使用Laplacian 算法经过无穷次迭代后，网格模型会收缩到其重心位置。Taubin 等［4］为了减缓因拉普拉斯算子引起的收缩现象，提出一种基于扩散的方法，并证明它是一种低通滤波器，具有抗收缩性。然而，Desbrun等［5］指出这种扩散方法是有缺陷的，因为它对网格的假设不现实。他提出一种基于曲率流的方案，在每个顶点计算局部曲率法向，并以其为基础进行扩散；Meyer 等［6］进一步扩展这种思想到各向异性的特征保持领域；之后，Kim 等［7］基于前3 个方法构造一个更为灵活的二阶滤波器GeoFilter框架，其中频率根据用户选择的特征自动计算以达到预期的结果。近年来，基于三维曲面的微分性质，一些学者提出一些基于优化的方法。He 等［8］将Xu 等［9］在图像平滑中使用的L0优化算法推广到网格去噪上，提出一种基于L0优化的算法。他将网格表面分段平坦区域最大化，因此能够在平滑的同时有效保持模型的几何特征。它们在高斯噪声情况下表现出色，但计算成本也很高，去噪结果随其他噪声类型的增加而恶化；Sun 等［10］使用L0正则化描述点集的平滑度并将其去噪；Cheng 等［11］针对非凸L0优化问题开发一种基于融合坐标下降框架的高效逼近算法，该算法可以获得梯度稀疏性好、与原始输入足够接近的解。然而，由于局部像素的高度一致性，在滤波输出中可能会产生更多的楼梯效应；Ahao 等［12］利用L0范数将顶点位置和顶点法向结合起来以衡量几何特征的稀疏性，进而提出一种改进的交替极小化求解框架。有些算法利用L1范数替代L0范数避免求解非凸问题，但在某些情况下这种近似会带来较大的误差；Wu 等［13］用L1范数构造数据保证项降低了异常值和噪声对算法的影响。L1范数求解容易，但是稀疏性比L0范数弱，所以在一些情况下可能得不到稀疏解，这类基于稀疏优化的方法能够有效保持尖锐特征；Wang 等［14］认为必须满足噪声独立分布的先决条件。所以，对于符合这些几何特征的模型可以生成很好的结果，如CAD 模型。而对于大噪声模型而言高阶微分性质很敏感，结果往往并不满意。滤波器通常是局部操作的，这些方法可以很好地恢复局部特征并且计算效率高。然而出于同样的原因，它们的性能往往因为表面存在较大噪声或不规则采样率而降低。

2 各向异性网格去噪方法

2.1 顶点双边滤波

双边滤波最初应用于图像去噪，它可在图像平滑的同时保留图像的边缘和细节。双边滤波的本质是高斯滤波的扩展，Jones 等［15］、Abedi 等［16］和Flesishman 等［17］将图像去噪中的双边滤波方法推广到网格去噪上。该方法在多数情况下能够有效去噪并保持特征，但由于算法假设网格是均匀采样的，对于高度不规则即大噪声的网格去噪效果不理想；Solomon 等［18］在前者基础上提出一种通用框架，可用于任意邻域的双边和平均移位滤波；Vialaneix 等［19］利用沿曲率方向的可分离滤波器进行近似网格双边滤波，以提高双边滤波运算速度；Wei 等［20］利用人脸法线和顶点法线来充分利用特征区域的互补性。这种基于滤波器的全局优化方法比基于稀疏性的方法更容易求解，并且很容易将现有滤波器组合起来，不会产生由强稀疏假设引起的副作用。然而，这些方法只使用两个高斯核和一些简单的几何属性（如正态差异）隐式地区分特征；Duguet 等［21］通过对点云数据的射流估计，将双边滤波扩展到基于表面曲率的二阶滤波。作为双边滤波方法的完善与推广，一些三边滤波算法［22-24］相继被提出。Choudhury 等［22］提出新的三边滤波器由Tomasi 等［25］双边滤波器改进而成，它将信号平滑到一个尖锐的分段线性近似。与双边滤波或各向异性扩散方法不同，三边滤波器在高梯度区域提供了更强的降噪和更好的孤立点抑制。Wang 等［23］提出一种基于能量最小化框架的特征感知三边滤波器用于三维网格去噪。该方法以两步法为基本框架，基于滤波器和全局优化方法的优越性以保持局部和全局特征并很好地对抗高噪声和不规则采样，而不需要二步求解方法、多步策略、训练数据等，不用担心过度拟合。与Choudhury 等［22］的滤波器不同，他们的滤波器以自适应邻域指示函数作为第3 个滤波器核。

2.2 面法向滤波方法

相比于网格的顶点信息，面片的法向信息更能体现网格表面的变化，即曲面特征信息，因为它是曲面上的一阶微分量。为解决面向顶点的双边滤波方法缺陷采用两步走（Two Step）方法，首先在网格的面法向量上进行一次滤波操作，然后根据校准后的面法向量进行顶点重建。

Zheng 等［26］首先将双边滤波器核集成到二次能量函数中进行全局法线优化。这项工作保留了特征，但性能受到双边滤波器的限制，因为噪声输入信号很难可靠地反映理想输出信号的几何形状。其法向滤波定义如下：

其中，n(ci)、ci、N(i)分别为面fi上的法向量、中心和邻域；Aij表示三角面fi、fj之间的权重参数，此处采用Aij为fi的面积；W(ci)为单位化系数；ωs、ωr为权重函数，分别表示网格上两相邻面fi、fj之间的位置相似性和法向信息相似性。当两个相邻面的法向量有着较大差异时，说明这两个面位于一尖锐边的两侧。ωr定义如下：

其中σr为函数ωr的衰减程度。

面法向之间的影响应该和面片之间距离成反比，因而可以采用欧氏距离的高斯函数来定义空间域权重：

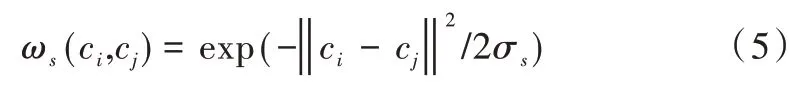
Yagou 等［27］在处理面部网格模型时使用均值过滤和中值过滤。均值滤波是邻域面片法线的加权平均值，由于均值滤波本身不是维持特征的滤波方法，因此该方法将破坏网格的原始特征；而中值滤波则是根据中心面片法向与邻域面片法向之间的夹角选取中值对应的法向作为滤波后的法向，在噪声较小的网格中，中值滤波能较好地保持原有特征，但在大噪声情况下结果并不理想。Yagou 等［27］提出一种α-截断滤波方法，通过选取不同的α得到均值滤波和中值滤波，因此这是均值滤波和中值滤波的折衷方法；Shen 等［28］提出一种基于最小二乘误差的法向和顶点位置更新的模糊中值滤波器，虽然效果比之前的方法更能保持特征，但是计算代价很大；Sun 等［29］将采样点的局部邻域限制在法向量的相似区域并对法向量进行修改。为了降低特征点的平滑性，提出一种基于双边滤波器的改进方法，用基于随机游走（Random walk）的权值对中心面片邻域内的法向量进行加权，用共轭梯度法过滤法线并求解顶点优化问题，从而保持网格特征；Zhang 等［30］提出分片常数空间及相应的微分算子，提出TV 法向滤波，滤波发现采用人脸模型面法向的变化总和可以描述更多的尖锐特征，获得良好的去噪效果，但是轻微的弯曲区域都会有明显的阶梯效应，且解要比L0方法少。这些方法虽然降低了求解难度，但也增加了更多约束，从而削弱了算法的鲁棒性。

2.3 引导法向滤波的去噪方法

双边滤波核函数有一先验条件，即邻近输入信号的差异与输出信号之间的差异相似。但这一假设并不总是成立，如果网格模型噪声过大则该假设将不再成立。因此，Zhang 等［31］提出一种导向滤波的网格去噪算法。相比双边滤波算法，引导滤波算法从原始模型上提取引导信号用于修改双边权值，为输出信号提供一个更为可靠的信息，可以更好地保持细节特征。该方法和Zheng 等［26］提出的方法相似，不同之处在于Zhang 等［31］采用联合滤波代替双边滤波。

对于网格面片fi的法向量ni做联合滤波处理，得到滤波后的法向ni：

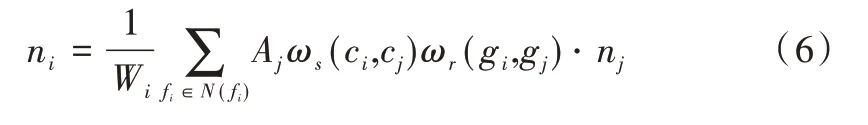
这里变量表示类似双边滤波的表达式，所不同的是函数ωr中采用了引导法向gi代替法向ni。

Wang 等［32］在Zheng 等［26］基础上提出滚动（Rolling）引导滤波，迭代过程中每一步都用原始的法向作为指导，更好地保持了原始模型的特征；Zhang 等［33］提出静态/动态（Static/Dynamic）引导滤波算法，其输入的引导网格被视为静态引导网格，迭代过程中不断更新的输出网格被视为动态引导网格，两者的特征信息相互结合，共同引导滤波过程；郭清华等［34］提出一种非线性引导滤波算法，它简便灵活，其核心是在网格面片的局部邻域内对引导网格的面片法向进行二次变换，得到法向场后，用Sun 等［35］的方法恢复网格顶点坐标，该算法可以有效防止在平滑过程中出现体积收缩、边缘模糊等现象，但是该算法每次迭代都需要调参以得到较好的引导网格；Liu 等［36］在引导滤波基础上通过特征探测识别特征面与非特征面，提出邻域选择的度量来增强特征，取得比指导滤波更好的效果，为了更有效地处理人脸网格模型，他们提出一种搜索算法来找到那些接近特征面并且具有相似几何特征的人脸，然后利用其指导滤波过程，最后根据滤波后的人脸法线更新顶点位置；Zhao等［37］使用图割（GraphCut）来生成分段平滑的块，并在其上建立指导法线。这些方案在复杂特征的合成网格上表现良好，但这些方案的主要思想是根据面法向差异找到一致的块，结构信息没有得到充分利用。扫描网格中包含多种噪声以及更复杂的形状，如锯齿噪声、阶梯状噪声和不规则的边，面法向的差异很大，所以很难区分噪声和特征。因此，要么导致伪特征，要么过度平滑。

2.4 数据驱动网格去噪方法

因为噪声网格可能包含各种不规则结构，这些结构被不同模式的噪声破坏。因此，利用特定的滤波器或先验假设去噪并不能一直产生令人满意的结果。此外，用户必须仔细微调各种模型参数。为了规避这些限制，数据驱动日益受到重视。Wang 等［38］提出了一种基于数据驱动的网格去噪技术——基于正态回归的方法。该方法可以在不假设面几何特征和噪声模式的情况下去除噪声。首先将滤波后的人脸法向描述子映射到真实输入的人脸法线，通过学习的方法得到非线性回归函数，然后应用所学习到的模型计算滤波后的人脸法线。在实时去噪过程中，首先获取噪声模型的特征，将其带入回归模型，得到与之对应的法向量，通过法向量重建模型。不同于各向同性的一些方法，该方法从训练数据中学习非线性去噪过程，对输入中的噪声分布和几何特征没有具体假设。算法先验条件为噪声只与其局部信息有关，如果噪声模型与真实模型差异太大将不能很好地完成去噪，所以其去噪效果依然存在一定缺陷。Wang 等［39］提出先从噪声模型和真实模型对中学习，使用噪声差异通过神经网络来移除噪声，然后将滤波模型和真实模型通过回归函数恢复特征。虽然这些数据驱动的方法能够在一定程度上学习去噪模式，不需要对几何特征和噪声模式进行特定假设，但它们仍然需要从噪声输入中手动提取几何描述符，例如Wang 等提出的面法向描述子（Facet NormalDescriptor）。

深度学习在图像处理中获得巨大成功，图形学研究人员也试图利用深度神经网络进行三维模型处理。然而，与具有规则像素网格结构的二维图像不同，三维模型具有不规则连通特性。因此，早期的工作探索了输入三维模型向网格结构的转换，例如体积表示［40-44］、深度图［45］、多角度图像［46］等等，通过数据转换就可直接使用深度神经网络来处理网格数据。

Zhao 等［47］提出了一种基于深度学习的网格面法滤波方案（NormalNet），第一次将神经网络用于网格去噪算法。提出了迭代训练框架，其中训练数据的生成和网络训练交替进行，真实法向作为导向滤波中的指导法线，得到目标法线，生成准确的引导法向并有效地去除噪声，同时保留原始特征并避免伪特征；Li 等［48］设计了DNF-Net，直接处理网格表面提取的局部块中的法向量。该方法不假设网格结构，也不将法线重新采样到网格中；直接处理网络每个块上的法向量以及局部三角形连接信息，并将其作为输入，输出去噪后的法向量。

这类方法训练过程很耗时，并且数据驱动方法都有一个共性缺点，即训练结果要受数据集影响。

3 其他方法

聚类信息可以从本质上消除各向异性表面的扰动。Dai 等［49］受此启发，设计了一种区域增长聚类方法，将有噪声的网格模型分割成块，再将常规的一些去噪算法如单边法向滤波（UNF）、双边法向滤波（BNF）、导向滤波（GNF）等算法应用到分块上，提高去噪效果。因为张量投票是几何处理中准确检测高质量网格特征的基本工具，一些基于张量投票法的网格去噪算法近来也被相继提出［50-52］。其中Wei 等［50］提出一个级联去噪框架，它们的方法包括多尺度张量投票、用于检测尖锐特征的顶点聚类方法和用于保留识别特征的分段拟合方法；岳少阳等［53］提出一种基于线性插值的、快速高效的网格模型去噪算法，其总体上将去噪模型看作是噪声模型和过分光滑模型的中间插值结果；Hurtado 等［40］选择邻域除了点和法向信息外考虑梯度信息来处理邻域。局部算法能够通过迭代逐渐恢复特征，但为了保持细节特征，局部算法的迭代次数往往很难自动设定。

低秩矩阵逼近方法［54-55］还用到网格去噪上，Li 等通过以法线场的形式探索三维网格上局部表面贴片之间的几何相似性，利用协方差矩阵找到相似的曲面片，设计了一个低秩恢复模型，该模型通过贴片组对法向量进行滤波，构造出相应的法向矩阵，进而通过低秩分解得到去噪后的法向。该算法虽然能够处理较大的噪声输入，但是和大多数非数据驱动类算法一样，对于特别大的噪声处理效果不理想。与此同时，如果模型中存在法向翻转也不能有效去噪。

4 实验结果与比较

除了从视觉效果比较各种方法性能，本节还介绍了3种常用的定量评价方法：均方角误差值（Mean Square Angular Error，MSAE）、基于顶点的L2误差度量和Hausdorff 距离。

4.1 均方角误差值

均方角误差值一般用来度量去噪前后法向的差异，其定义为：

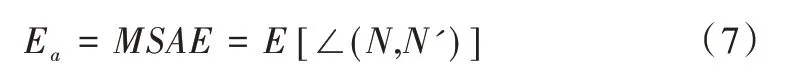
E表示期望值。MSAE的值越小，说明去噪前后面法向量越接近，表明滤波效果越好。

4.2 基于顶点的L2 误差度量

该方法定义为：

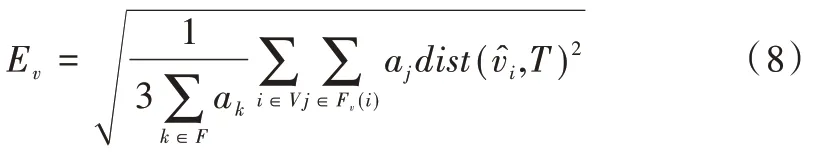
其中F、V、a分别表示面集、顶集和三角形面积。dist(,T)表示去噪后顶点与原始网格中与该顶点相邻的面片T最近的距离。

4.3 Hausdorff 距离

Hausdorff 计算得到的距离越小，说明去噪后的顶点距离真实平面越接近，去噪效果越好［56］。

设X和Y分别为两个度量空间(M,d)非空子集，Hausdorff 距离定义如下：

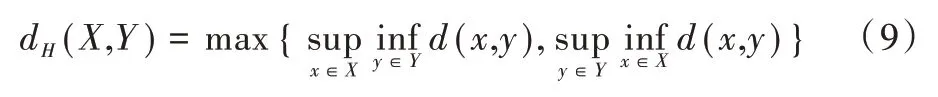
其中，sup 表示上确界，inf 表示下确界。

4.4 去噪算法的比较与分析

下面分析常见的几种去噪算法对标准网格模型的处理结果，模型包括细节较少的Eight 网格模型、细节丰富的Gargoyle 网格模型，CAD 模型Part_Lp 网格模型和Kinect 真实扫描的David 网格模型。

由图2 可知，对于细节较少的模型大部分算法都能得到较好的效果。其中非迭代方法和Tabin 方法视觉上表现稍逊，但是从表1、表2 可以发现，这两种方法在定量分析上表现却很出色。在处理CAD 模型时，双边滤波方法和非迭代方法并不能有效平滑噪声，而拉普拉斯平滑算法过渡明显平滑，网格的边缘特征已经被消除；Tabin 算法模型恢复得不是很好，因为其主要适用于大噪声模型［57］。双边法向滤波在处理标准CAD 模型时体现了其保持特征的优势，模型棱角信息保留较好。但是，从图3 可以发现，对于细节丰富的模型，双边法向滤波会丢失细节。L0算法虽然可以去除噪声，但是模型边缘地方会变扁。

Fig.2 Comparison of denoising results of various denoising algorithms for models with less details图2 各种去噪算法对细节较少的模型去噪结果比较

对于细节丰富的模型，如图3 所示，导向滤波算法结果较好，但显著的边缘特征仍存在瑕疵，一些边和尖角发生了扭曲，因为导向滤波方法适合复杂特征的合成模型；但是对于不规则噪声，如真实扫描模型中的噪声，面法向的差异很大，所以很难区分噪声和特征，因此要么导致伪特征，要么过度平滑。而基于数据驱动的方法，如RoFi 和级联回归去噪效果良好［58］。从图4 和图5 可以发现，同样都是细节丰富的模型，使用L0算法去噪结果却相去甚远，因为L0算法对参数敏感。

Fig.3 Comparison of denoising results of CAD models by various algorithms图3 各种算法对CAD 模型去噪结果比较

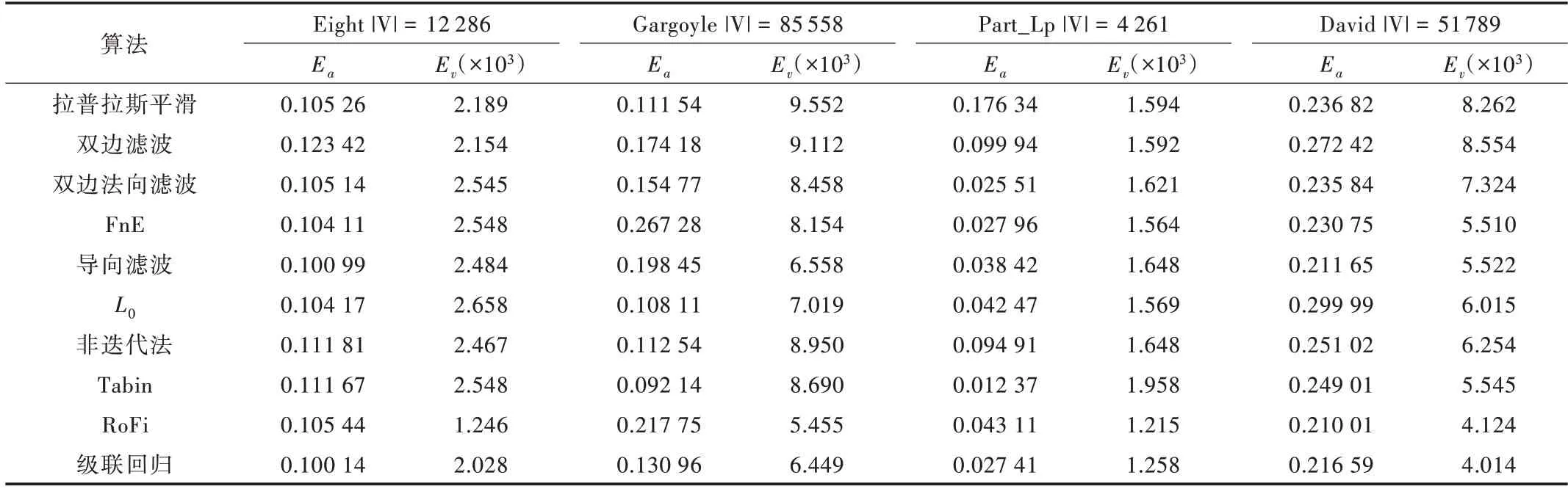
Table 1 Comparison of average angular error and error metric of various algorithms表1 各种算法的平均角误差Ea 和L0 误差度量Ev 的比较

Fig.4 Comparison of denoising results of various algorithms for models with rich details图4 各种算法对细节丰富的模型去噪结果比较

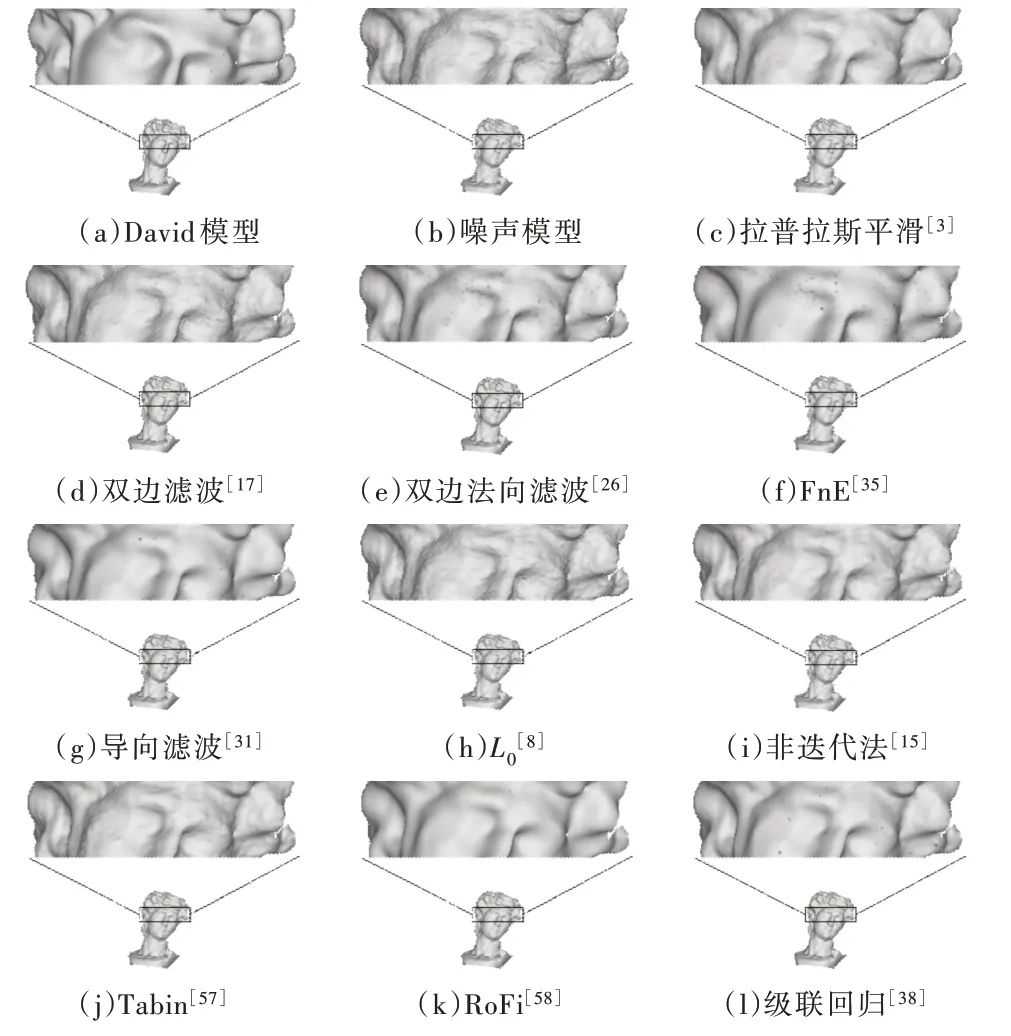
Fig.5 Comparison of denoising results of real scanning model by various algorithms图5 各种算法对真实扫描模型去噪结果比较

对于真实的扫描模型，如图5 所示，基于学习的方法，如RoFi 和级联回归都能在保持原有特征的前提下较好地完成去噪。而双边滤波、L0平滑、非迭代法都未能得到好的效果，说明基于学习的方法更能胜任相对复杂的噪声模型的去噪。这类方法的缺点是某些假设可能并不总是得到满足，但是即使在高噪声或不规则采样率下也可获得良好的结果和全局特征，因为它通过优化将误差分布在整个表面。

Table 2 Hausdorff distance between the denoising results of various algorithms and the original model表2 各种算法去噪结果与原始模型的Hausdorff 距离

5 结语

三维网格建模在计算机图形学领域应用是一个基础性研究课题，在游戏、电影行业发挥着重要作用。网格去噪是建模过程中重要的一步。本文总结了近年来网格去噪算法的一些研究成果，旨在帮助读者快速了解该领域的研究进展。

深度学习和神经网络技术在图像领域的飞速发展促使越来越多的研究者尝试将其应用到三维图形上，这是一个具有挑战性且十分有意义的研究。到目前为止，还没有一个算法能够达到完美的去噪效果，这些算法都是在去噪与保特征之间博弈。RoFi、NormalF-Net、级联回归、Normal-Net 等算法效果都较好，但是大多数网络结构还不能接受三维数据的直接输入，仍需要一些表示算法作为辅助。同时，大量训练数据的获取、算法的优化、效率提升都是需要考虑的问题。