基于客车稳定杆的载荷谱获取方法优化及应用

陈婉平， 郑炳峰， 廖家清, 纪绪北， 张雅鑫

(比亚迪汽车工业有限公司， 广东 深圳 518118)

1 背景

某4款客车(用不同型号的稳定杆)在道路试验中稳定杆发生断裂，其中A款客车断了3根同一型号稳定杆，其余B、C、D 3款客车均只断了1根稳定杆。4款客车稳定杆断裂位置均在转角弯弧处。对断裂稳定杆进行材料试验，结果显示断裂稳定杆的材料性能满足要求。

采用文献[1-2]中所述的方法，对上述不同型号的4种断裂稳定杆(与上述4款客车对应，分别记为A、B、C、D)进行有限元静力分析与疲劳分析。分析输入的载荷来源于失效稳定杆工况复现，路试采集应变谱，经计算转换获取载荷谱。稳定杆B、C、D静力分析的最大应力分别为722.8 MPa、977.2 MPa、1 267.7 MPa，大于材料屈服强度(1 274 MPa)的50%；疲劳分析寿命次数与路试断裂次数的比值分别为0.74、0.84、1.39，接近1.0。考虑材料、加工等离散性，疲劳分析能较好地估算稳定杆的路试寿命。可见，采用文献[1-2]中所述方法，估算稳定杆的寿命是可行的。

采用相同的方法，稳定杆A的静力分析最大应力为398.0 MPa(见图1)，约为材料屈服强度的31%；疲劳分析的寿命次数约为270万，路试断裂的寿命次数却为2万，比值为135。

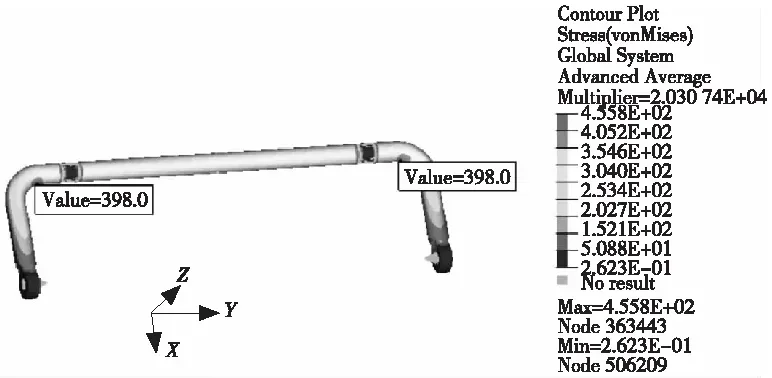
图1 静力分析应力云图_未优化方法获取的载荷

查找稳定杆A分析结果与实际路试存在大的偏差的因素是静力分析与疲劳分析时输入的载荷偏小。其原因：项目时间紧迫、杆件备件不足，仅用1根稳定杆进行载荷数据采集；试验员不认真，设置数据采集器测得应变转换成实际表面线应变的比例系数有误；优化前的载荷获取方法缺乏相应的校验措施。

而稳定杆B、C、D，试验员对相应型号的3根样件进行反复试验，并对采集的载荷数据进行反复对比分析、验证，然后取出试验载荷值作为输入进行仿真分析，与路试结果基本一致。

为提高所获取试验载荷谱的准确性，使仿真分析能更准确地预测稳定杆路试断裂风险，减少载荷谱获取过程中人为因素的影响，下面将对载荷谱获取的方法进行优化。

2 实测应变与理论载荷转换

客车稳定杆外形大体上呈“C”型，其力学简化模型[3-5]如图2所示。车辆行驶轮胎随路面上下跳动，两侧车轮出现垂向反向跳动或侧倾时，稳定杆两侧端头处产生垂向力而发生扭转变形，产生防止车辆倾覆的侧倾力矩，保证整车安全性和舒适性。

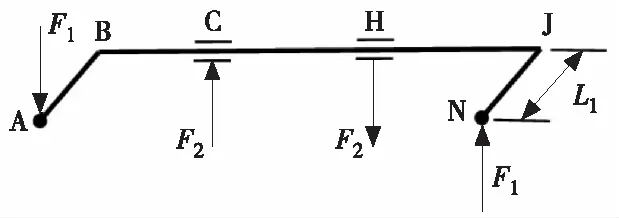
图2 稳定杆受力的数学模型

用扭转应变片测量稳定杆中间位置与轴线成45°方向上的表面线应变(以下简称为表面线应变，记作ε45°)，将其转换成端头加载点的理论载荷。图2中，端头部位A、N点为稳定杆的外接点；C、H点为稳定杆的内接点；J、N点间的距离称为垂臂长，记为L1。

下面推导稳定杆中间位置测得表面线应变ε45°与端头加载力的转换关系。

测得表面线应变ε45°后，由文献[6-7]可知：

ε45°=-γ/2,τ=Gγ,τ=T/Wt

(1)

而BJ段扭矩T=F1L1,则

F1=-2GWtε45°/L1，令K=-2GWt/L1

(2)

则有：

F1=Kε45°

(3)

式中：γ为稳定杆中间位置的剪切应变；τ为剪应力；G为材料的剪切模量；Wt为截面的抗扭截面系数；F1为两外接点的加载力；K为稳定杆中间点的扭转线应变为1 με时对应的加载力。

3 优化前载荷谱获取

3.1 优化前载荷谱获取方法

优化前载荷谱获取方法即是利用公式(3)计算的过程，具体如下：

1) 粘贴应变片。

2) 工况复现，采集稳定杆中间位置的表面线应变ε45°，得实测应变谱。

3) 利用公式(3)计算稳定杆端头加载点的载荷谱F1。

根据上述流程，在nCode软件中的实现过程如图3所示[8]。

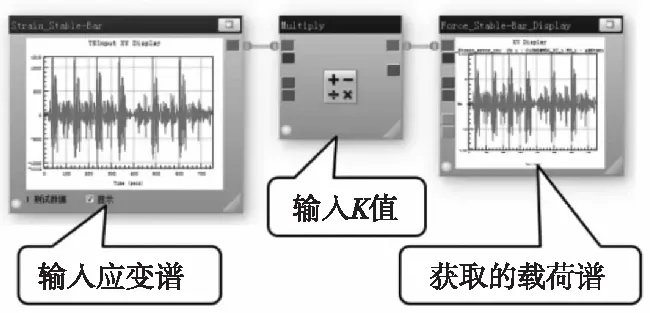
图3 未优化方法获取载荷谱的nCode流程

3.2 优化前载荷谱获取方法的缺陷

优化前载荷谱获取方法的缺陷主要有：

1) 粘贴应变片时，受试验人员经验影响，其位置可能出现偏差，采到的应变数据不准确。

2) 无校核数据准确性的措施，无法排查应变谱数据的偏差，最终计算结果与实际不符或偏差较大。

3) 为得到可靠的稳定杆载荷谱数据，需对多根稳定杆贴应变片进行道路试验，对比采集数据的一致性。这将增加试验时间和成本，且效率低下。

4 优化后载荷谱获取

4.1 优化后载荷谱获取方法

优化后的稳定杆载荷谱获取方法，其流程如图4所示。其主要步骤如下：

1) 首先进行稳定杆的台架标定[6，9-10]试验(图4虚线框内示意)，得到表面线应变与端头加载力的标定线性方程。

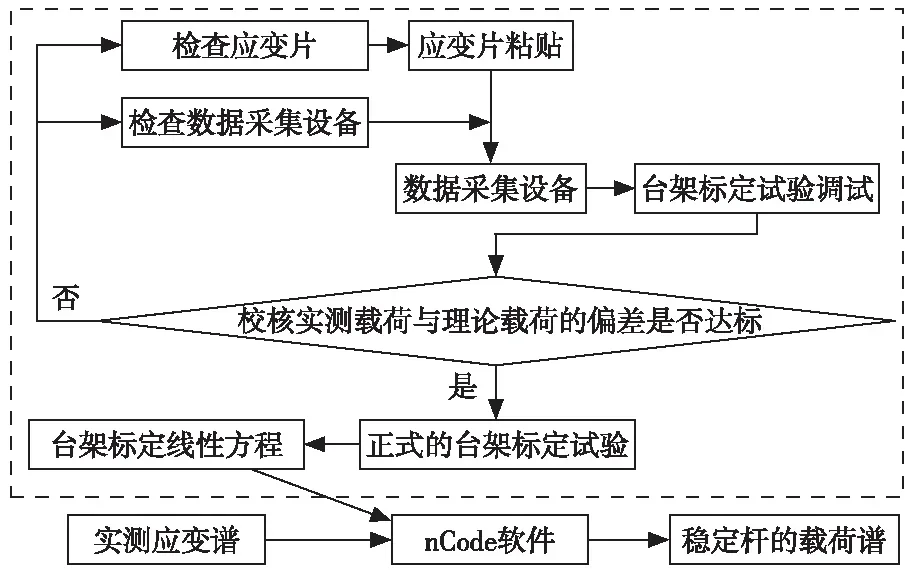
图4 优化方法的流程示意图

2) 然后进行工况复现，采集路试中稳定杆中间位置的表面线应变ε45°，得到实测应变谱。

3) 最后在nCode软件中，根据标定线性方程与实测应变谱，计算稳定杆端头加载点的载荷谱。

4.2 台架标定试验

如图5所示，在稳定杆3的中间位置，粘贴测量ε45°的扭转应变片；将稳定杆按实车的安装方式固定在试验台架上，稳定杆一端固定，另一端刚性连接到液压缸4上，稳定杆安装固定处用V形金属支承块2支撑。

图5 稳定杆台架标定试验示意图

参照商用车稳定杆标准[9]中刚度试验的方法，控制液压缸加、卸载一次，加、卸载力为±Fmax，Fmax是将2 000 με(ε45°的值)和式(2)算得的K值代入式(3)计算得到，如稳定杆A对应的Fmax值为42 kN；然后再控制液压缸对稳定杆进行加、卸载，记录3组以上稳定杆实测应变与液压缸实际加载力的数据。将实测应变数据和式(2)算得的K值代入式(3)，计算液压缸理论加载力，然后比较计算理论加载力与实际加载力的偏差。若偏差在±15%以内，则开始正式的台架标定试验。否则，按图4虚线框内的流程，对台架标定试验进行检查。

进行正式的台架标定试验，液压缸加载力的过程为0→Fmax→0→-Fmax→0，加载3个循环，每间隔2 kN手工记录试验过程中的应变与加载力的多组数据，对同一加载力下的应变数据取均值。

绘制所测表面线应变与加载力的散点图，用最小二乘法线性拟合加载力与应变的关系曲线，如图6所示，并得到台架标定线性方程：

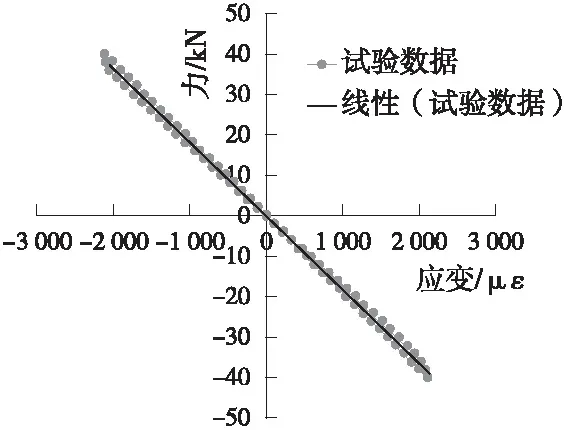
图6 应变与加载力关系及拟合曲线

F=kx+b

(4)

式中：k为垂向应变刚度；x为稳定杆中间位置的表面线应变ε45°；b为线性方程的截距；F为稳定杆端头位置的垂向加载力。

4.3 优化方法获取载荷谱

将台架标定后的稳定杆安装到实车上，工况复现，采集应变谱。根据台架标定线性方程、路试实测应变谱，在nCode软件中获取稳定杆载荷谱如图7所示。采用该方法可有效克服3.2节中所述缺陷。

图7 优化方法获取载荷谱的nCode流程

5 优化前、后载荷谱偏差分析及应用效果

以稳定杆A为例，方法优化前、后获取的稳定杆载荷谱如图8所示。

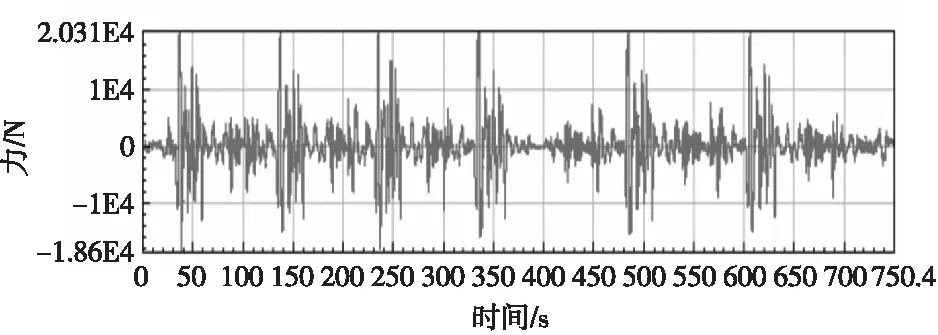
(a) 未优化方法获取的载荷谱

表1为方法优化前、后获取的载荷谱极值，两种方法载荷的偏差大于15 000 N。载荷的偏差将导致有限元静力分析与疲劳分析的结果出现严重偏差，对判断稳定杆是否断裂产生较大影响。

表1 方法优化前、后获取的载荷谱极值 N

以断裂稳定杆A为例，加载方法优化前、后获取的载荷谱进行有限元静力分析与疲劳分析。

1) 静力分析。未优化方法的静力分析结果已在第1部分中介绍。在优化方法获取的载荷作用下，稳定杆的最大应力为722.8 MPa，小于材料的屈服强度1 274 MPa，但该应力值大于材料的疲劳极限720 MPa[11]，存在断裂风险。方法优化后的分析结果与方法优化前的完全不同，而且相差较大。

2) 疲劳分析。加载方法优化前、后获取的载荷谱，对断裂的稳定杆A进行应变疲劳分析。

①计算稳定杆全局损伤分布，预测稳定杆损伤热点。如图9所示，稳定杆A的损伤热点为弯弧处的PL、PR点。

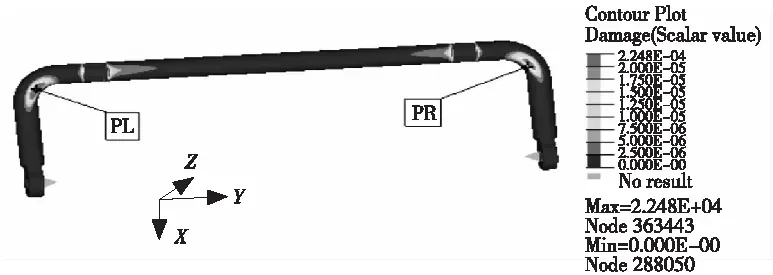
图9 稳定杆A的损伤热点

②在nCode软件中，在损伤热点处，粘贴虚拟应变花，获取热点位置的应变谱，对应变谱进行雨流计算[12]，结合材料的应变疲劳曲线，计算稳定杆损伤热点处的寿命。

稳定杆A损伤热点PL、PR处的单次循环寿命损伤及疲劳寿命见表2。方法优化前、后获取载荷谱预测的寿命约为270万次、1.5万次，结果相差大。

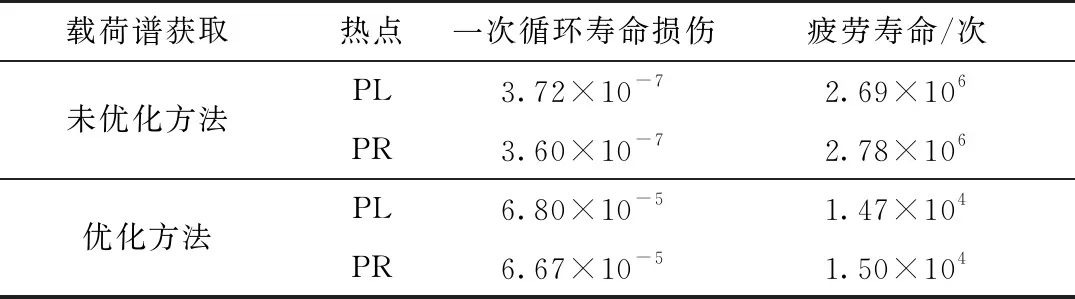
表2 不同载荷谱的热点损伤与寿命

如第1部分所述，实际路试中，稳定杆A的断裂寿命约为2万次，与优化方法获取载荷谱计算的疲劳寿命比值约为0.75，接近于1.0。考虑稳定杆材料、加工等分散性，用优化方法获取的载荷谱进行应变疲劳分析，可预测稳定杆的实际寿命。优化的载荷谱获取方法具有更高的准确性和可靠性。

6 结束语

本文以研究稳定杆断裂为基础，指出了稳定杆载荷谱获取方法优化前的缺陷，提出了优化载荷谱获取的方法，最后通过仿真与路试对比分析，表明了优化的载荷谱获取方法具有更高的准确性与可靠性。本文思路可用于其他类似的问题。