基于循环生成式对抗网络的一维时变信号自适应去噪研究*

董骏捷，唐 建，周然之，杨超越

（陆军工程大学野战工程学院，南京 210007）

0 引言

信号去噪是信号处理的重要环节。经典的去噪方法有小波分解［1-3］、经验模态分解［4-6］（Empirical Mode Decomposition，EMD）、奇异值分解［7-8］（Singular Value Decomposition，SVD）等。其中小波分解和SVD本质上都是选取某一种核，对含噪信号进行分解后，去除掉被认为是噪声的部分，重构后得到降噪信号。这类基于核的方法，需要依赖人的经验去选择核和确定阈值，自适应性差，在用于时变信号去噪时，效果往往不佳。EMD是一种依据信号本身特性的自适应分解方法，但其存在着过冲-欠冲及边界效应，导致信号在逐层分解与重构过程中出现失真。

近年来，深度学习领域中的生成式对抗网络［6］（Generative Adversarial Networks，GAN）发展迅猛，以其良好的数据生成能力、泛化能力、自适应能力，在图像去雾、去雨滴等问题上取得了良好应用，其本质上也是二维信号的去噪问题，为一维时序信号的去噪带来新的思路。

1 GAN的发展

原始GAN最初由Goodfellow等在2014年提出。其由生成器Generator和判别器Discriminator两大部分组成。如图1所示，生成器G根据输入的随机序列z来产生尽量服从真实数据分布Pdata（x）的生成样本G（z），以欺骗判别器D，而D的作用是判断输入样本是真实样本x还是生成样本G（z）。在G与D的交替训练过程中，两者之间相互对抗，互相促进，最终达到纳什均衡，使G能够生成高度逼近真实分布的G（z），而D则由于无法正确区分x和G（z），其输出最终会逼近一个固定值。

图1 GAN的原理Figure 1 Principle of GAN

GAN的目标函数如下所示：

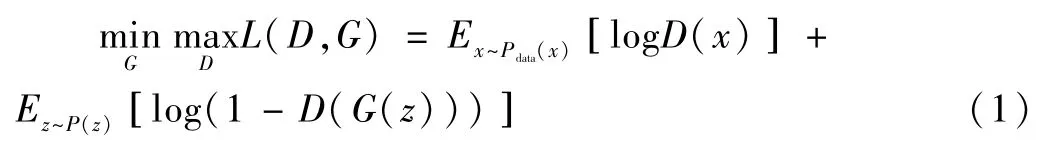
原始GAN一经提出，立即衍生出大量改进模型，如DCGAN、AC-GAN、CC-GAN、InfoGAN、LSGAN、SGAN、DualGAN、CycleGAN、BGAN等。其中，2015年，Alec Radford提出的深度卷积GAN（Deep Convolutional GAN，DCGAN），将卷积神经网络与GAN结合起来，把原始GAN的G和D所采用的多层感知机模型均改为CNN结构，大大优化了原始GAN的性能，该结构也多为其他衍生模型所借鉴。2017年，Kim提出了CycleGAN（Cycle-Consistent Generative Adversarial Networks），顾名思义，其是由两个镜像对称的GAN构成的环形网络。该模型可以实现两类有一定相关性的样本的相互转换，即通过无监督训练，使得生成网络学习到两类样本空间相互间的最佳映射。CycleGAN在图片风格迁移领域取得了成功应用，而信号去噪也是某种意义上的信号风格迁移，因而同样可利用该方法来实现信号去噪。

2 基于CycleGAN的自适应去噪

2.1 去噪模型整体结构及原理

基于CycleGAN的自适应去噪，就是寻求信号从含噪空间到无噪空间的最佳映射关系的过程。为实现这一目标，需要构建含噪信号和无噪信号两类样本集，对CycleGAN进行训练，从而获得两个生成器。其中一个生成器以含噪信号为输入，以无噪信号为输出，也就是实现了端到端的自适应去噪功能。去噪CycleGAN的结构及原理如图2所示。

图2 去噪CycleGAN的结构及原理Figure 2 The structure and principle of denoising CycleGAN

两个对称的GAN共享两个生成器GAB和GBA，分别完成从含噪信号样本空间A到无噪信号样本空间B的映射与逆映射，并各自带一个判别器DB和DA。DB用于分辨真实的无噪信号与生成的伪无噪信号；DA用于分辨真实的含噪信号与生成的伪含噪信号。一个单向GAN存在由G损失和D损失组成的一组对抗损失，一对镜像的GAN就存在GAB与DB、GBA与DA这两组对抗损失。

对于GBA与DA，对抗损失函数如下所示：

对于GAB与DB，对抗损失函数为：

此外，CycleGAN还增加了一项循环一致性损失，即要求任意一个信号依次通过两个生成器后，得到的重构信号能够与自身尽可能一致，即要求：

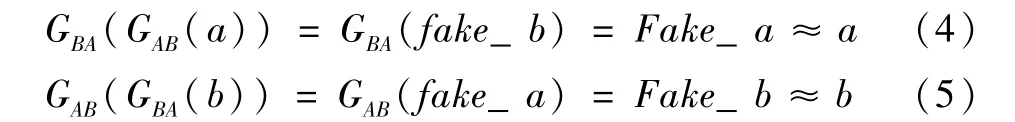
循环一致性损失函数表达式为：

至此，整个CycleGAN的总损失函数即为两组对抗损失和一组循环一致性损失之和：

2.2 判别器和生成器结构

本文所搭建的CycleGAN，其镜像的两个GAN均采用一致的DCGAN结构。

判别器由5层卷积神经网络组成。其输入为样本库的真实信号和生成器的生成信号，输出是一个1×32的判别向量，根据该向量与0向量和1向量的欧氏距离的大小，判定输入信号是真实信号还是生成器生成的假信号。

生成器的结构可分为编码器、转换器和解码器3大部分。编码器通过3层卷积模块，将1个输入信号压缩成256个特征向量；转换器由9层残差模块组成，通过组合信号的不相近特征，将信号在含噪域中的特征向量转换为无噪域中的特征向量；解码器则利用反卷积层完成从特征向量中还原出低级特征的工作，最后得到的输出是1个生成信号。

3 实验及结果分析

3.1 数据集及评价指标

实验所用训练数据集由A集和B集组成，各为5 000个无噪与增加了信噪比为1的高斯白噪声的含噪信号；测试数据集由随机生成的信噪比分别为0.5、1、1.5、2、2.5、3的含高斯白噪声的时变信号各200个组成。每个信号采样频率均为为1 000 Hz，长度为256，经一化处理。

实验采用信噪比SNR（Signal Noise Ratio）和均方误差MSE（Mean Squared Error）来评判去噪效果。其中，SNR用以评价噪声的去除情况；MSE用以评价去噪后的信号与真实信号之间的一致性。

3.2 实验步骤

首先，用训练数据集A集和B集对搭建的CycleGAN网络进行训练，待到对抗性损失与循环一致性损失收敛到稳定值时，停止训练，保存模型，此时的生成器GAB即学习到了从含噪域A到无噪域B的最佳映射；随后，选取信噪比分别为0.8、1、1.5、2、2.5、3的1～6组含噪信号测试集，分别输入具有去噪功能的生成器GAB，将输出的去噪结果再分别与小波阈值去噪结果进行定量对比，通过SNR和MSE两个指标来评判其去噪性能。

3.3 实验结果分析

图3～4所示为各组测试集的200个含噪信号用不同方法去噪后，信号的信噪比和均方误差的分布情况。6组测试结果的均值如表1所示。可知，CycleGAN去噪均方误差远小于小波阈值法，信噪比远高于小波阈值法。

图3 不同方法去噪后信号的MSE分布对比Figure 3 MSE distribution of signals denoised by different methods

图4 不同方法去噪后信号的SNR分布对比Figure 4 SNR distribution of signals denoised by different methods

图5～6分别从时域上和时频域上直观地展现了CycleGAN去噪的优良效果。可见，CycleGAN去噪有效克服了小波阈值法去噪在面对低信噪比信号时设定的阈值一刀切地将有用信号也当做噪声去除这一不足，通过模型的循环对抗训练，得到了具备自适应映射能力的生成器，对噪声能量较高的含噪信号也能很好地去噪，近乎逼真地还原为无噪信号。此外，生成网络具有良好的泛化性能，能将其他不同信噪比的含噪信号也很好地从含噪空间映射到无噪空间。

表1 不同去噪方法的实验结果对比Table 1 Experimental results of different denoising methods

图5 时域上的去噪效果比较Figure 5 Denoising effects in the time domain

图6 时频域上的去噪效果比较Figure 6 Denoising effects in the time-frequency domain

4 结束语

本文以寻找信号从含噪域到无噪域的最优映射的思想为指导，构建了一维CycleGAN去噪网络，对一维时变信号自适应去噪方法开展了研究。实验结果表明，该方法得到的去噪生成器，面对低信号比的时变信号具有比传统方法更优越的自适应去噪能力，并且具备良好的泛化性能。但对于生成器与判别器究竟如何学习到含噪信号与无噪信号的特征及其相互映射，尚不明确其数学原理。CycleGAN去噪的内部黑箱机理，值得下一步重点研究。