改进神经网络的电子音乐辨识研究
赵婕
(陕西工业职业技术学院 信息工程学院, 陕西 咸阳 712000)
0 引言
音乐可以给人们带来精神上的享受,消除人们身体和精神疲劳,减轻工作上的压力,由于电子技术不断地发展,一些专业人员通过电子设备进行电子音乐的合成,产生了大量的电子音乐,给人们提供了更多的音乐欣赏素材,但是由于每一个人对电子音乐都有自己的偏好,如老年人喜欢听一些旋律比较慢的古典音乐,而年轻人喜欢听一些快节奏的摇滚音乐,因此帮助人们对电子音乐进行有效辨识,给他们提供最适合的电子音乐具有十分重要的意义[1-3]。
由于国内外学者们的重视,当前有许多类型的电子音乐辨识方法,其中人工神经网络的电子音乐辨识方法最多,如回声状态网络的电子音乐辨识方法,BP神经网络的电子音乐辨识方法,RBF神经网络的电子音乐辨识方法、极限学习机的电子音乐辨识方法等,由于人工神经网络的工作原理与人脑的神经网络工作原理相似,可以模拟人脑对电子音乐进行辨识,电子音乐辨识效果较好,其中BP神经网络的实际应用范围最为广泛[4-6]。在实际应用过程中,BP神经网络还有许多难题没有得到有效的解决,如BP神经网络的结构不稳定,使得电子音乐辨识效果极不稳定,可信度比较低,导致电子音乐辨识效率低,而且学习速率采用经验方式随机确定,使得电子音乐辨识误差比较大[7-9]。
针对神经网络在电子音乐辨识过程中存在的参数优化问题,为了改善电子音乐辨识结果,提高电子音乐辨识精度,提出了改进神经网络的电子音乐辨识方法,采用自适应遗传算法快速、有效地寻找最优的参数,使得神经网络结构达到最优,测试结果表明,改进神经网络的电子音乐辨识精度高、速度快,具有十分明显的优越性。
1 改进神经网络的电子音乐辨识方法
1.1 BP神经网络
由于BP神经网络的学习能力强,与电子音乐辨识过程具有较强的相似性,标准BP神经网络常采用3层结构,如图1所示[10]。
电子音乐辨识特征为x1,x2,…,xm,其直接作为BP神经网络的输入,那么其相应的输出为式(1)。
(1)
隐含层的输入、输出分别为式(2)、式(3)。
(2)
(3)
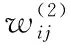
输出层的输入、输出分别为式(4)、式(5)。
(4)
(5)
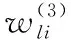
采用电子音乐辨识误差作为BP神经网络的训练目标,BP神经网络的训练过程实际就是不断对隐含层和输出层的连接权值进行调整,使电子音乐辨识误差朝最小化方向发展,如式(6)、式(7)。
(6)
(7)
式中,η为学习速率。
参数学习速率η直接影响BP神经网络的隐含层和输出层的连接权值确定的优劣。η越大,隐含层和输出层的连接权值变化量比较大,使得BP神经网络的学习速度快,但是过大,可能使得BP神经网络出现过拟合现象,即学习精度降低;而η越小,隐含层和输出层的连接权值变化量比较缓慢,BP神经网络的学习速度慢,影响学习效率。当前主要通过经验方式确定η,难以获得理想的BP神经网络的学习效果,为此本文采用自适应遗传算法确定参数学习速率η的值,在加快BP神经网络学习速度的同时,提高BP神经网络的学习精度。
1.2 自适应遗传算法
遗传算法的性能与交叉概率(Pc)和变异概率(Pm)直接相关,标准遗传算法的交叉概率和变异概率采用固定方式,在其运行过程中是一个常量,难以产生优异的后代个体,使得遗传算法易限入局部最优解,因此本文采用自适应遗传算法,其交叉概率和变异概率随着进化代数的变化而变化,这样不断产生优秀个体,避免限入局部最优解。自适应遗传算法的Pc和Pm变化曲线如图2所示。
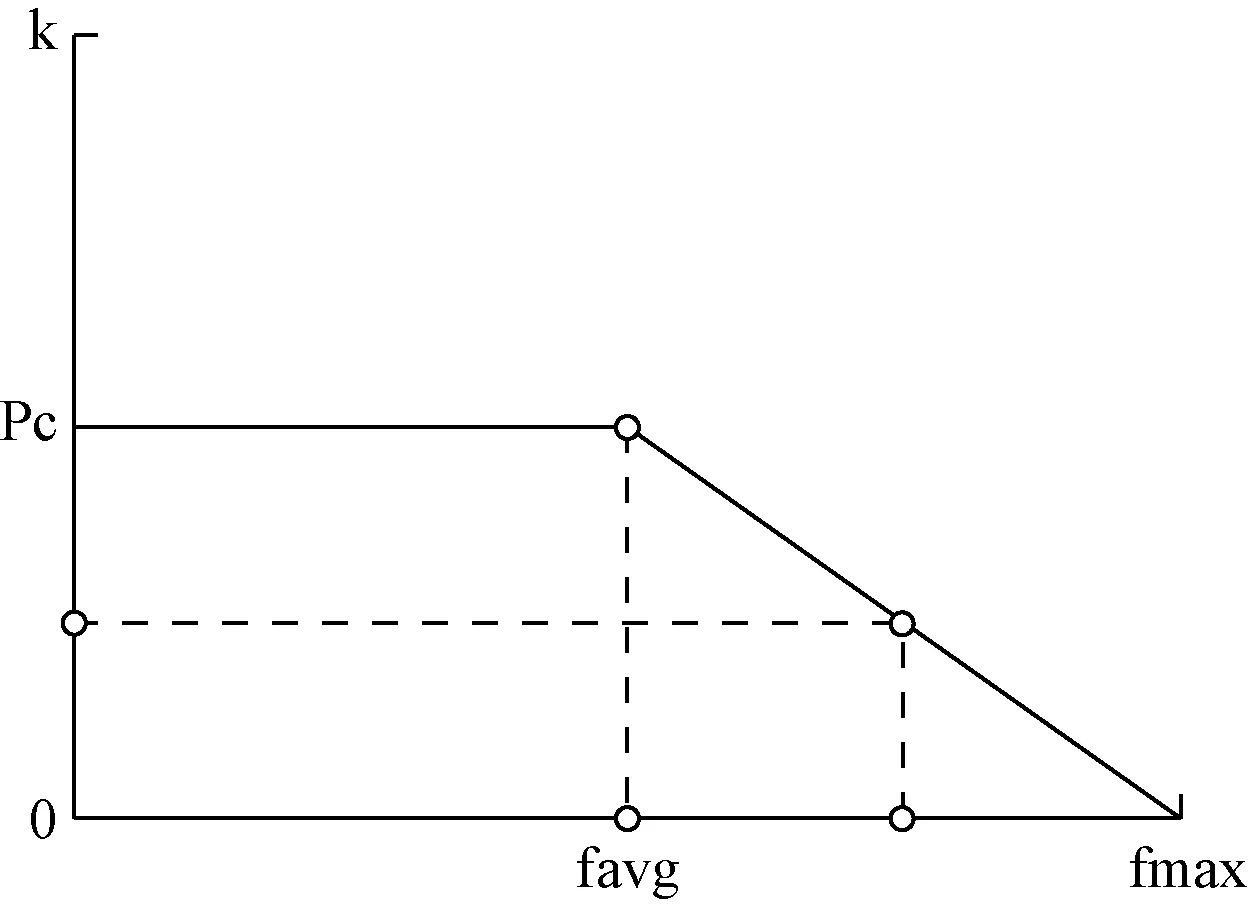
图2 交叉变异概率变化曲线
自适应遗传算法的Pc和Pm的计算式,如式(8)、式(9)。
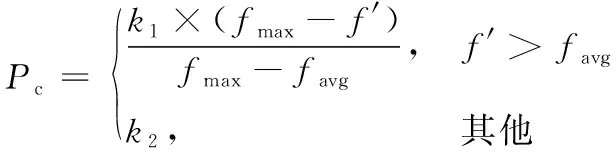
(8)
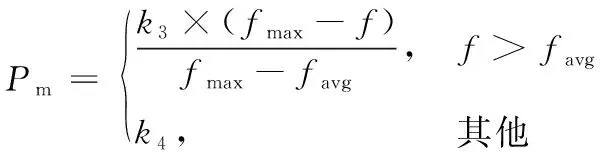
(9)
式中,fmax和favg分别为适应度函数的最大值和平均值;f′为交叉后较优个体的适应度函数值;f为变异后的个体适应度函数值;ki为0—1范围的常数。
1.3 提取电子音乐特征
本文采用电子音乐信号的短时能量特征、时域方差特征进行电子音乐辨识,它们提取步骤具体如下。
Step1:Em为电子音乐信号{y(n)}的能量,那么其短时能量计算如式(10)。
(10)
式中,c(m)为电子音乐信号的滑动窗,电子音乐信号帧长度是N。
Step2:电子音乐信号可以划分为N帧,即可以表示为Yt(n)={yt(n,1),yt(n,2),…,yt(n,N)},计算电子音乐时域的均值Ei(n)和方差Di(n),如式(11)、式(12)。
(11)
(12)
1.4 改进神经网络的电子音乐辨识步骤
Step1:采集电子音乐信号,并对其进行去噪处理,以提高电子音乐信号的信噪比。
Step2:从去噪后的电子音乐信号中提取短时能量特征、时域方差特征,并对它们进行归一化处理,如式(13)。
(13)
式中,feature(i)表示第i个特征。
Step3:对于每一种电子音乐信号,选择比较重要的特征进行建模。
Step4:根据电子音乐信号的重要特征数量和电子音乐的类型数量确定BP神经网络的输入和输出节点的数量。
Step5:根据一定的规则,确定电子音乐信号辨识的BP神经网络隐含层节点的数量。
Step6:采用自适应遗传算法确定BP神经网络参数学习速率η的值。
Step7:BP神经网络对电子音乐信号训练样本进行学习,建立最优的电子音乐信号辨识模型。
2 仿真实验
2.1 电子音乐辨识实验样本数据
为验证改进神经网络的电子音乐辨识效果,选择当前最流行的10类种电子音乐作为实验对象,而且对于每一类电子音乐,采集不同数量的电子音乐样本,如表1所示。
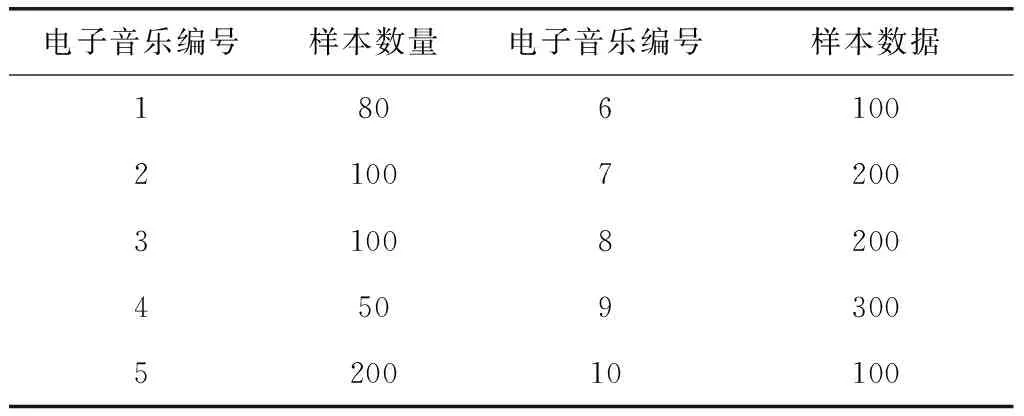
表1 10种电子音乐的样本数量
2.2 不同电子音乐的特征数量
由于电子音乐的类型不同,那么其特征数量应该不同,因此提取不同的电子音乐特征,并选择比较重要的特征进行电子音乐辨识,得到的重要特征数量如表2所示。
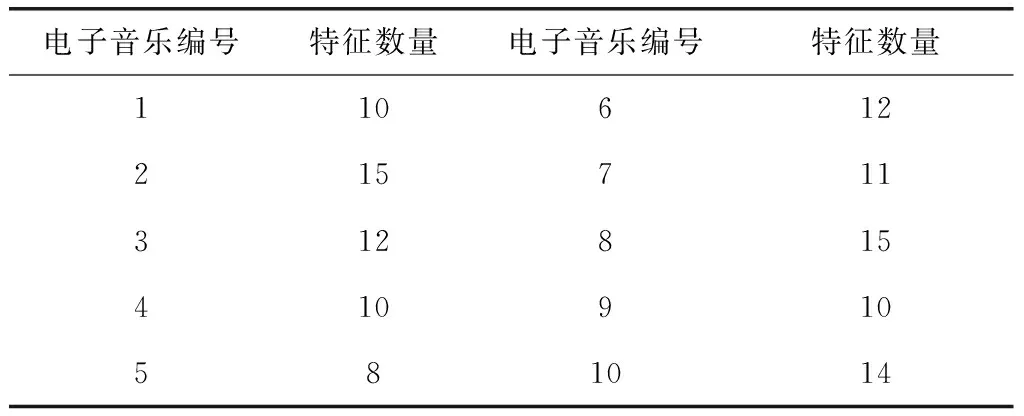
表2 10种电子音乐的重要特征数量
2.3 与传统神经网络电子音乐辨识结果对比
为了验证本文对神经网络改进的有效性,选择传统神经网络进行电子音乐辨识对比实验,传统神经网络采用经验方式确定其参数,改进神经网络和传统神经网络的电子音乐辨识精度和时间,如图3、图4所示。
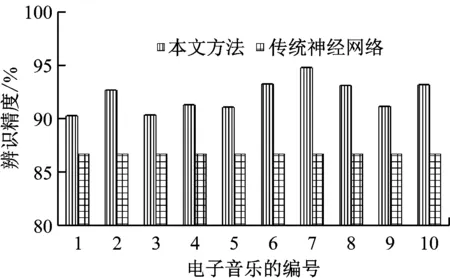
图3 与传统神经网络的电子音乐辨识精度对比
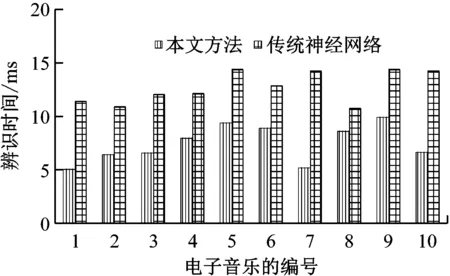
图4 与传统神经网络的电子音乐辨识速度对比
从图3和图4可以看出,无论是电子音乐辨识精度或者是电子音乐辨识速度,改进神经网络均要明显优于传统神经网络,这是因为改进神经网络引入自适应遗传算法解决了参数优化的难题,能够获得更优的神经网络,建立了高精度的电子音乐辨识模型,而且加快了电子音乐辨识速度,在相同时间可以辨识更多的电子音乐辨识样本,这样可以降低电子音乐辨识成本,实际应用价值更高。
2.4 与经典电子音乐辨识方法的结果对比
为了进一步测试改进神经网络的电子音乐辨识的优越性,选择当前经典电子音乐辨识方法进行对比实验,具体为:隐马尔可夫模型的电子音乐辨识方法[11]、支持向量机的电子音乐辨识方法[12],所有方法的电子音乐辨识精度如图5所示。
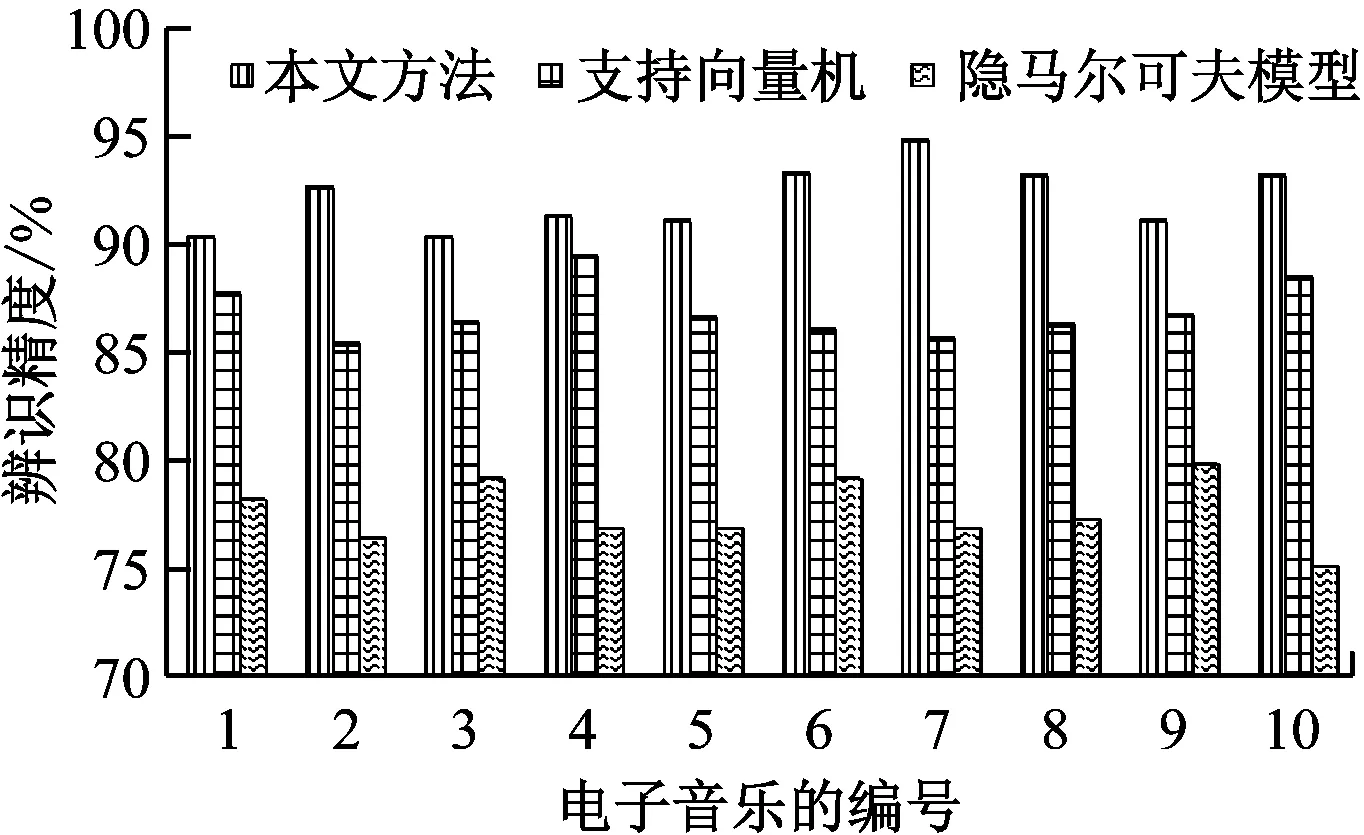
图5 与经典电子音乐辨识方法的精度对比
从图5可以看出,相对于支持向量机、隐马尔可夫模型,改进神经网络的电子音乐辨识精度均有了不同程度的得升,这表明改进神经网络可以有效减少电子音乐辨识错误率,能够准确辩识各种电子音乐,改进神经网络可以解决当前电子音乐辨识方法存在的弊端,获得了更加理想的电子音乐辨识结果。
支持向量机、隐马尔可夫模型、改进神经网络的电子音乐辨识时间变化情况,如图6所示。
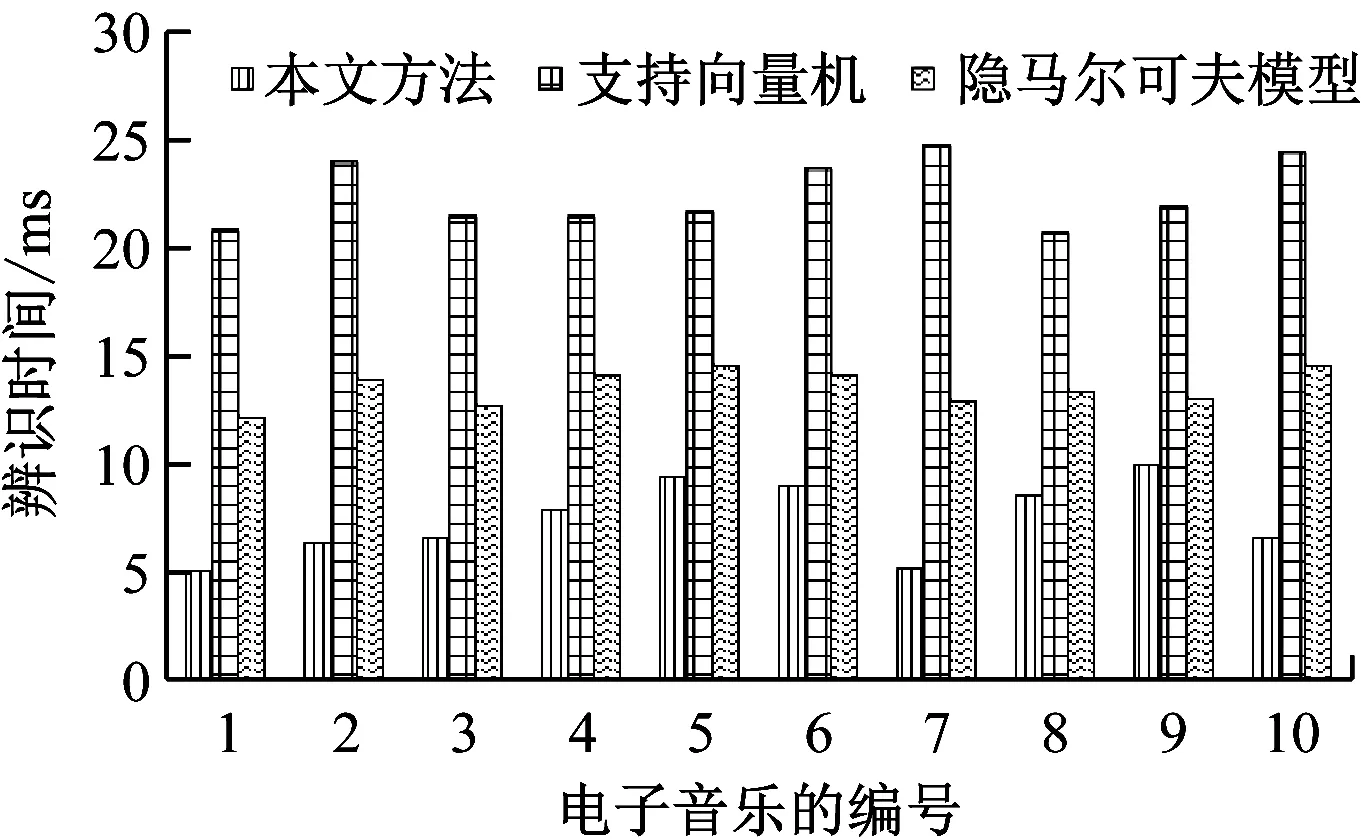
图6 与经典电子音乐辨识方法的速度对比
对图6的电子音乐辨识时间进行对比可以清楚看出,相对于支持向量机、隐马尔可夫模型,改进神经网络的电子音乐辨识时间明显减少,改进神经网络的电子音乐辨识时间复杂度明显降低,提高了电子音乐辨识效率,电子音乐辨识速度得到了明显的改善。
3 总结
为了改善电子音乐的辨识精度,针对当前神经网络存在的缺陷,提出了改进神经网络的电子音乐辨识方法,并与其它方法进行了电子音乐辨识仿真实验,通过对仿真实验结果分析可以发现,改进神经网络的电子音乐辨识精度高,不仅错误率要小于其它电子音乐辨识方法,而且电子音乐辨识速度快,具有十分广泛的应用前景。

