复合实验方法研究温度对管线钢氢脆的影响
邢 潇, 李凤英, 刘建国, 崔 淦, 李自力, 罗小明
(中国石油大学(华东)储运与建筑工程学院,山东省油气储运安全重点实验室,山东青岛 266580)
0 引 言
随着能源工业的发展,高强度的X系列钢材成为能源运输中应用最广泛的材料。在长输油气管道建设中,随着钢材强度的增加,管道壁厚可以相应减小,因此,管道建设成本可以大幅度降低。然而,高强管线钢,如X80、X90钢材随着强度的提升,氢脆敏感性会显著增强,导致管道止裂性能大幅度降低[1-2]。据加拿大能源公报显示,38%的管道失效是由氢脆导致的断裂引起的。温度是对氢脆影响最严重的外部条件,研究温度对管道氢脆断裂失效的影响,对于预测和防止事故的发生具有重要的意义[3]。
氢脆的研究存在多个尺度的研究方法。Xing等[4-5]通过传统的电化学实验方法发现随着提高近中性pH溶液的温度,钢材的基体氢浓度会显著提升。Beck等[6]通过拉伸实验,并辅助以扫描电镜(SEM)检验氢扩散率与温度的关系,得到氢扩散率与(-1/T)存在指数关系。Jiang等[7]通过有限元模拟的方法,确定了氢原子在钢材中的跃迁路径为四面体间隙,并确定氢原子扩散系数Do为0.15 mm2/s。Hou等[8-9]通过分子动力学模拟确立了氢原子运动速率与裂纹扩展速率的关系,并量化了两者的正相关性。Dadfarnia等[10]的模拟研究显示,位错会囚禁氢原子,直到饱和后,多余的氢原子才能继续向裂纹尖端扩散。因此,只有在裂纹前端未被囚禁的氢原子,即自由氢原子可以对裂纹的生长做出贡献。
温度对氢脆的影响,既涉及化学反应,又涉及力学性能,单一的实验方法无法满足研究的需要。为了明确温度对管道氢脆的影响,本文提出了宏观-微观-纳观结合的跨尺度复合实验方法。宏观上通过拉伸实验和渗氢电流密度实验确定不同温度下的钢材断面收缩比和不同温度下的钢材基体氢浓度;微观上通过扫描电镜观测试样断面的特征,确定断裂温度阈值;纳观上,通过分子动力学模拟,确定氢原子扩散率与温度的关系。最终通过量化不同温度下氢原子扩散到裂纹尖端,并使裂纹尖端应力集中区饱和的速率,来预测管线钢氢脆温度阈值。
1 实验材料与方法
实验材料选用国产X90管线钢,其主要化学成分如表1所示。室温下,其抗拉强度为675 MPa,屈服强度为592 MPa,伸长比为26%。

表1 X90钢的主要化学成分(质量分数,%)
1.1 慢应变拉伸实验
慢应变拉伸(SSRT)实验试样沿管道环向取样,以保证试样拉伸时主受力方向与工程上管线的主受力方向一致,并参照国家标准加工成如图1(a)所示试样。实验前将试样编号并取中间段30 mm进行标距,在标记范围之外用704硅胶密封,用水砂纸将标距区域表面逐级纵横交错打磨至1 500#,打磨方向与拉应力方向一致,以避免磨痕对裂纹萌生的影响。打磨后依次用丙酮、去离子水和酒精清洗,以去掉表面油脂和杂物,冷风吹干后放入干燥器中干燥24 h备用[11]。

图1 试样与拉伸试验示意图(mm)
本实验的实验介质为标准NS4模拟溶液[12],采用分析纯试剂和去离子水配制而成,本试验温度范围内pH为6.6~7.1。拉伸实验前先缓慢通入纯度为99.5%的N2,对溶液进行除氧处理,时间为1 h,以保证实验在无氧环境条件下进行。实验过程中持续加入5%CO2+95%N2以维持近中性pH环境。
为研究温度的影响,本实验设计了可以用于控制局部温度的腐蚀箱。该装置如图1(b)所示。实验过程中,试样的标距部分始终浸没于腐蚀箱中的NS4溶液中,腐蚀箱周围夹层中通入循环流动的恒温液体(10℃以下采用酒精,10℃以上采用纯净水)来控制NS4溶液的温度。恒温液体由恒温槽(型号为DC-2006)来控制,并通过磁力驱动循环泵循环流动。采用深圳万测试验设备有限公司生产的ETM-105D型微机控制电子万能试验机对试样在不同温度的NS4模拟液(0、10、20、30、40和50℃)中进行SSRT实验。所有拉伸实验的应变速率均为1×10-6s-1。实验前先施加490N的预载荷,以消除减速齿轮、夹具等的间隙[4]。试样拉断后,用除锈液超声清洗,酒精擦拭并吹干。测量试样断口面积和延伸量,计算试样的断面收缩率和延伸率。并采用扫描电镜(SEM)对试样断口及侧面的形貌进行观察。
1.2 Devanathan-Stachurski电化学实验
电化学渗氢实验采用Devanathan-Stachurski双电解池,其装置如图2所示,两个电解池互不相通,工作电极即测试试样,辅助电极为厚度为几百μm的金属铂片。阴极池为充氢电解池,阴极池的工作电极与辅助电极连接直流电源,可对试样进行恒电流或恒电位充氢。充氢时试样为阴极,接通电流iC后,在阴极上产生原子氢,一部分原子氢复合成分子氢释放;另一部分扩散进入试样内部。阳极池为测试电解池,相应的试样面称为测试面。阳极池的三电极系统连接电化学工作站,其作用是在测试面上加适当的氧化电位,将由试样的阴极面渗透过来的原子氢完全氧化,从而产生阳极电流iA,该电流可被电化学工作站采集记录。实验全程采用氮气驱氧。随着电化学渗氢实验的进行,阳极电流密度随时间而逐渐增大,最后趋于一个稳定电流密度值i∞。由此可得金属基体氢浓度c0=J∞L/Deff。其中:J∞为氢扩散通量;L为样品厚度;Deff为有效氢扩散系数。
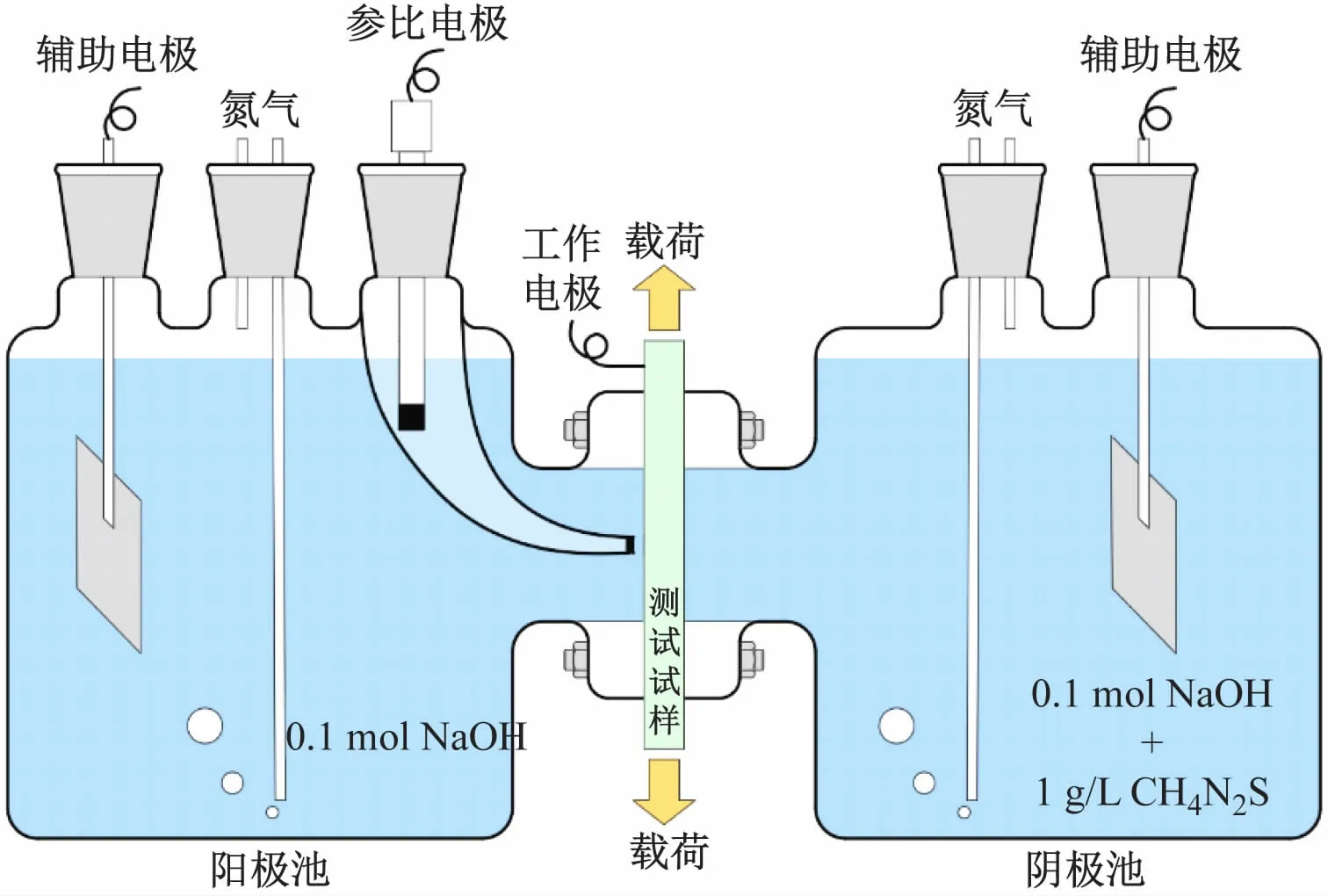
图2 Devanathan-Stachurski实验装置示意图
1.3 分子动力学模拟
模拟系统包含55 297个铁原子和54个氢原子,系统的体积为(7×10×10)nm3。周期性边界条件被分别施加到和z-[ 110] 3个方向。模拟利用正则系综(NVT)[13-14]调整系统原子的速度,使用Nose-Hover[14-15]方法调整系统的温度。通过嵌入原子势能(EAM)调整原子间的相互作用[16-17],其中Fe势能由Mendelev研发,根据密度泛函理论(DFT)[17]计算得到的大量能量和原子构型数据库被用于拟合H和Fe的交叉相互作用。系统采用单晶体心立方结构ɑ铁,如图3所示,所有的模型都在300 K温度下建立,其后再对模型进行温度处理。
2 实验结果与分析
2.1 慢拉伸实验结果分析
X90钢试片在空气中293K下和在NS4溶液中不同温度下的应力应变曲线如图4所示。不同曲线的弹性模量没有显著区变,但是在断裂前的伸长比率有明显不同,在空气中的伸长比率明显高于在NS4溶液中的伸长比率。另外,应力应变曲线末端投影到x轴上覆盖的面积在空气中也明显最大,说明X90钢试样在空气中的韧性也是最大的。因此由图可知,在NS4溶液中的试样发生了明显的氢脆现象。

图3 单晶体心立方结构ɑ铁

图4 不同温度下NS4溶液中X90试片应力应变曲线
试样断裂前的伸长比δ和试样断面的收缩比φ这两个参数可以用来定量试样受到氢脆影响的程度。伸长比和收缩比越大,则试样的韧性越好,受到氢脆的影响越小。在图5中,伸长比和收缩比呈现一致的变化趋势,趋势可以记为:273 K>283 K>333 K>323 K>293 K>303 K>313 K(δ,φ)。前人研究表明,在空气中,随着温度升高,物质的韧性增强,脆性下降。在NS4溶液中,由于氢脆现象的存在,这种规律被打破。试样在273~283 K条件下,韧性最好。在283 K以上韧性急剧下降,直到在313 K韧性达到最低。在温度继续升高后,试样韧性反而升高,在333 K时恢复到与283 K相似的韧性。上述结果表明,X90钢材在313 K时氢脆最为剧烈,容易发生断裂失效。

图5 不同温度下NS4溶液中X90试样断裂时的伸长比和断面收缩比
为了直观比较不同温度下,受氢脆影响的X90钢材的韧性,SEM拍摄的断面图片可以作为参考。为了简化比较过程,只把303~323 K的断面图片在图6中展示。在同样的分辨率下,303 K和323 K下的试样断面上有明显的韧窝和河状裂纹,而313 K下的试样断裂面相对平整,没有明显的韧性断裂特征。另外313 K下的试样断面面积明显更大,且无明显的断面收缩现象,进一步印证了313 K下的断裂为脆性断裂。

图6 NS4溶液中的拉伸实验后试样断面SEM图
2.2 Devanathan-Stachurski实验结果分析
体积氢浓度与钢材的强度无关,因此X80钢中的渗氢电流密度可以在本研究中被应用[4]。渗氢电流密度对应的是图7中的平台值i∞。而钢材基体氢浓度与电流密度的换算公式为:co=i∞lz/(FD)。其中:F为法拉第常数;lz为试样的厚度。由图可知,i∞随温度的升高显著增加。然而co的值不仅与i∞相关,也与氢原子的扩散系数D相关,而D的数值也随温度增加而增加,因此欲得到co值与温度的关系,也要量化D与温度的关系。
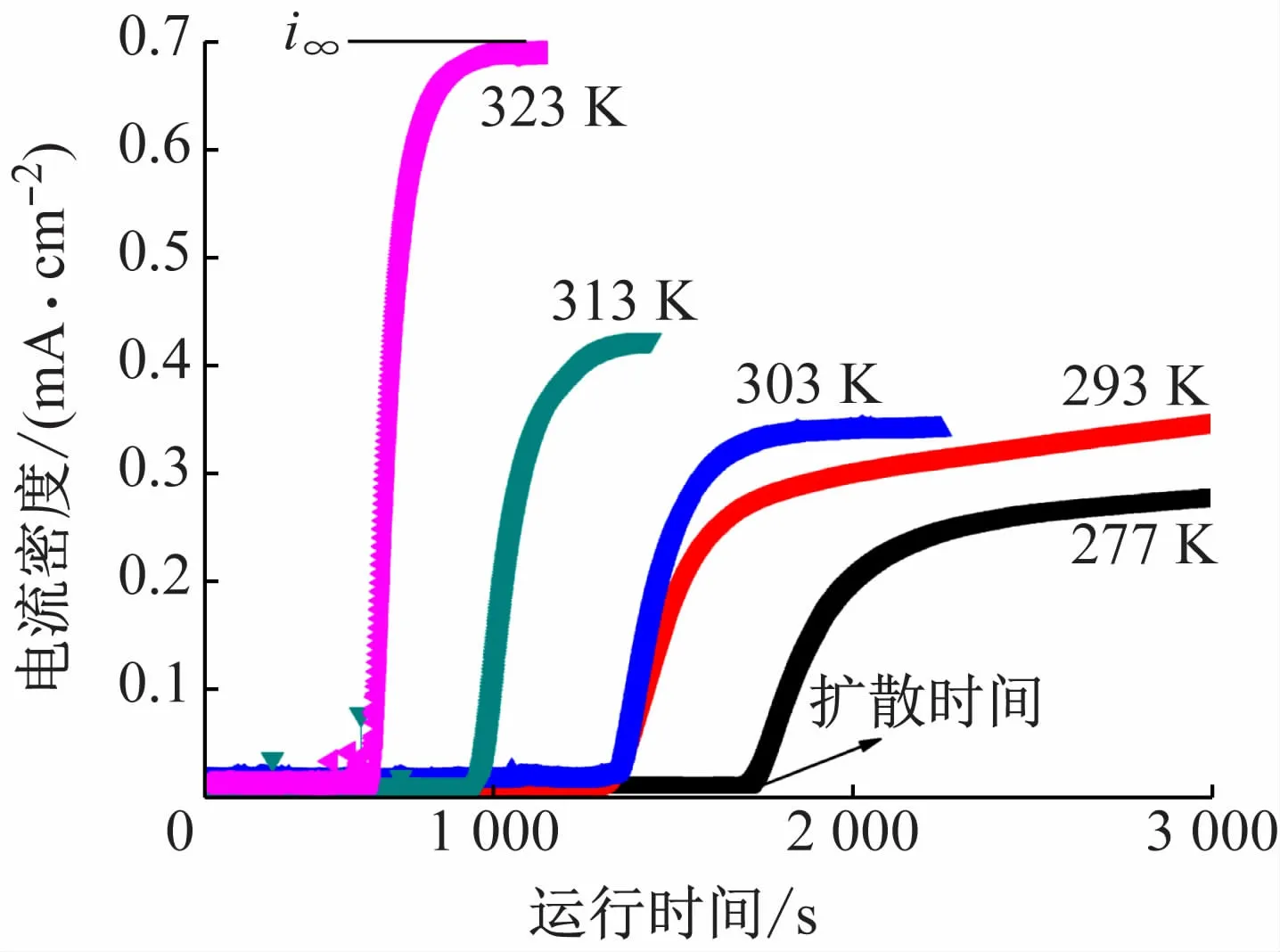
图7 不同温度下X80钢试样的渗氢电流密度
2.3 分子动力学模拟结果分析
模型在所需温度下处理500 ps后,使用下式可以计算氢原子在不同温度下的均方位移(MSD)。

式中:d表示计算所涉及模型的轴向,体扩散时该值等于3;N是氢原子总数;r(to)是H原子的初始位置;r(to+Δt)是时间间隔Δt之后氢原子的位置,结果如图8(a)所示。通过获得MSD曲线的斜率与时间的关系,可以计算得到扩散率D,如图8(b)所示。结果表明,温度促进了钢材中氢的扩散。
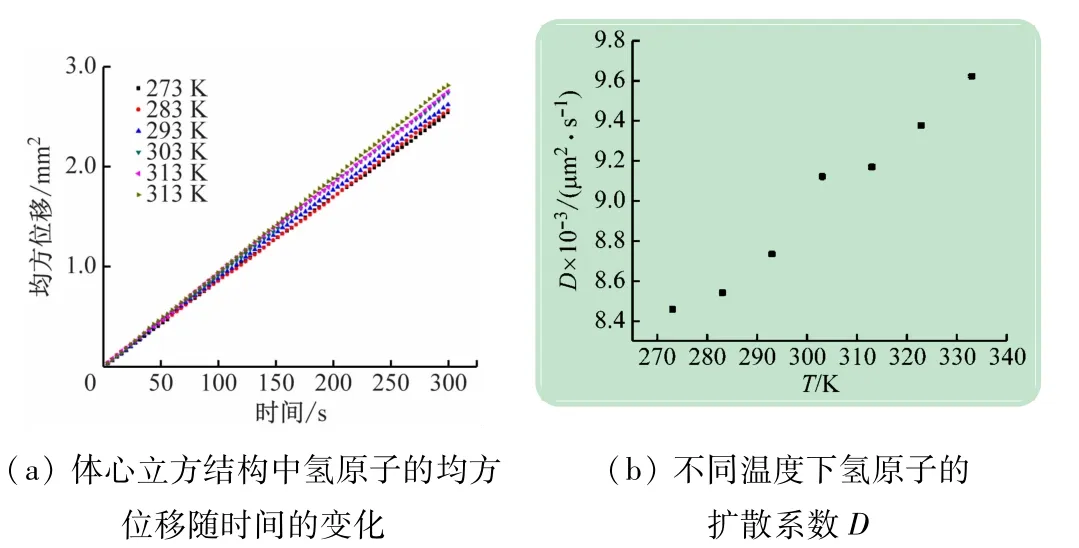
图8 在体心立方结构中氢原子均方位移和扩散率随时间的变化关系
扩散率D与温度T的函数关系,

式中:Do是扩散常数,特征值为0.15 mm2/s[7];kB为玻尔兹曼常数;T是温度;Eo是扩散势垒,范围在0.035~0.142 eV之间,根据模拟拟合的值为0.08 eV,与经验结果吻合良好。
2.4 温度对X90钢氢脆的影响
氢脆的剧烈程度取决于氢原子填充微观裂纹尖端应力集中区所需的时间,所需时间越短,则氢脆程度越强。为了研究这一过程,选择了微裂纹产生作为参考。微裂纹周围的应力分布为

式中:v为X90钢的泊松比;KI是裂纹尖端的应力强度;r是从特定位置到裂纹尖端的距离。特定温度和应力强度下的平衡氢浓度[5]可以表示为
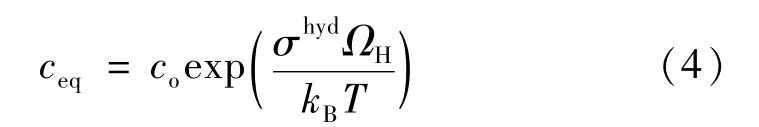
式中,ΩH是氢原子在钢材中的组分体积。氢致开裂速率与氢原子向微裂纹尖端累积的速率有关。然而,氢原子需要优先饱和裂纹尖端之前的集中应力区。随后,剩余的可扩散氢原子扩散到裂纹尖端,使裂纹扩展。假设裂纹尖端前方的纳米圆形区域将捕获氢原子并阻止氢扩散到裂纹尖端。如果该区域能够更快地被填充饱和,则氢脆断裂更容易发生。因此,应力集中区填充饱和所需氢原子总数与氢移动速度之比可用于表征氢脆的水平。
氢原子向裂纹尖端富集的速率[5]为
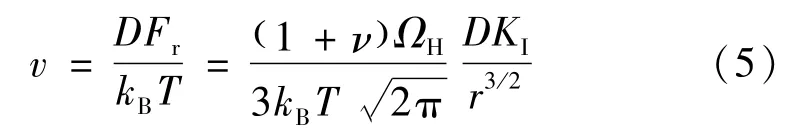
纳米富氢区域的尺度选择根据Song[9]的模型为R≈160 nm,则填充饱和该区域需要的总氢原子数为
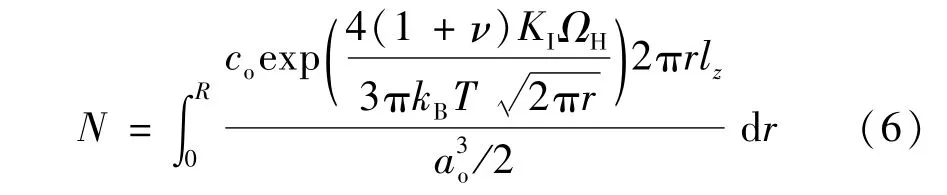
如前文所述,N/v的比值可以表征不同温度下氢脆的程度。其值越小,代表应力集中区被氢原子填充饱和的速率越快,即氢脆程度越剧烈。图9展示了N/v值随温度的变化。结果显示,在温度为313 K时,这一比值达到最小,即在此温度下,X90钢的氢脆最剧烈。

图9 不同温度下X90钢的N/v比值
3 结 语
(1)本文采用宏观实验、微观检测、纳观模拟相结合的复合实验手段,明确了温度对管线钢氢脆程度的复杂影响。
(2)氢脆的剧烈程度取决于可扩散氢原子到裂纹尖端的填充速率。温度的升高,增加了氢原子的移动性,同时也增加了裂纹尖端应力集中区可以捕获的氢原子量,但是两者增加的趋势不一致,因此存在一个阈值,使得管线钢氢脆断裂最严重。
(3)X90管线钢的氢脆温度阈值为313 K,大于该温度,氢脆随着温度升高而减弱,小于该温度,氢脆随着温度升高增强。因此X90钢材的工作环境应当尽量避免这一温度,以减弱氢脆的影响。通过这一复合实验方法,明确不同管线钢材的氢脆温度阈值,对于管线钢运行、操作、维护有重要意义。

