半潜式起重铺管船起重机吊高与跨距的优化配置

徐京阔 李立涛 黄山田 刘顺庆 秦立成 李新超 孙文明

(海洋石油工程股份有限公司，天津 300461)

0 引言

大型起重机的吊载起重量和吊载的幅度的匹配是决定起重机最主要的性能的关键，扒杆的长度、宽度和吊高与跨距的关系确立后可更加充分并且合理的利用扒杆的性能。

起重机吊高与跨距的关系是一个相对的矛盾体，即当被吊载物体提升到一定的高度后，容易与吊臂的下弦杆产生干涉问题，所以既需要吊臂长一些且截面小一些，符合吊臂与被吊载物不产生干涉，又需要吊臂短一些且截面大一些，符合吊载重量较大的要求。因此，找到二者都满足的平衡点比较困难。以往做法通常是设计好吊臂，通过作图法测绘吊载物体在一定幅度和高度下是否与吊臂干涉，如果出现干涉，局部修改吊臂本身，计算吊臂的弦杆应力，循环反复。通过循环反复的试凑法让其满足吊载，整个过程十分繁琐，每次排图后需要计算吊臂的主弦杆应力，因此需要优化二者关系，以达到最好的匹配。

1 研究方法——基于粒子群算法改进的蚁群算法

蚁群算法是一种用来寻找优化路径的概率型算法，它由Marco Dorigo于1992年在他的博士论文中提出，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。蚁群算法在求解复杂优化问题方面具有一定的优势，在一般函数优化问题中也证明有明显的效果，对于函数不连续、不可微、局部极值点密集等情况，具有较好的优化能力。

粒子群优化算法是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法，该算法由Kenndy和Eberhart于1995年提出。通常单个自然生物并不是智能的，但是整个生物群体却表现出处理复杂问题的能力，群集智能就是这些团体行为在人工智能问题中的应用。微粒群优化最初是处理连续优化问题的，目前应用已扩展到组合优化问题。由于其简单、有效的特点，已经得到了众多学者的重视和研究。

粒子群算法虽然具备较快的全局搜索能力，但没有较好地利用系统中的反馈信息，易形成冗余迭代，求解效率低；蚁群算法具有较好的全局收敛能力和并行性的优点，且易于与其他方法相结合，但算法初期信息素不足，易使算法的速度变慢。

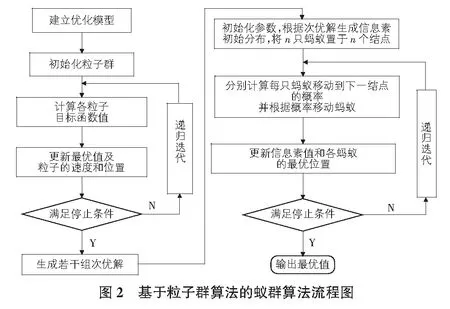
为了更好的发挥上述两种算法的优点，弥补各自的缺陷，形成优势互补，首先利用粒子群算法快速的全局收敛对优化问题进行前期搜索，将得到各粒子的历史最优位置值转化为下步蚁群算法的信息素初始分布，再利用蚁群算法的并行性、正反馈性及求解效率高的特性，将上述最优位置值作为后期蚁群算法各个蚂蚁的位置，同时将信息素初始分布重新设置。这样融合后的改进算法，时间效率上优于粒子群算法，在求解效率上优于蚁群算法，形成了时间效率和求解效率都比较好的改进算法。

2 实例计算分析

2.1 数学模型

1)模型的建立。

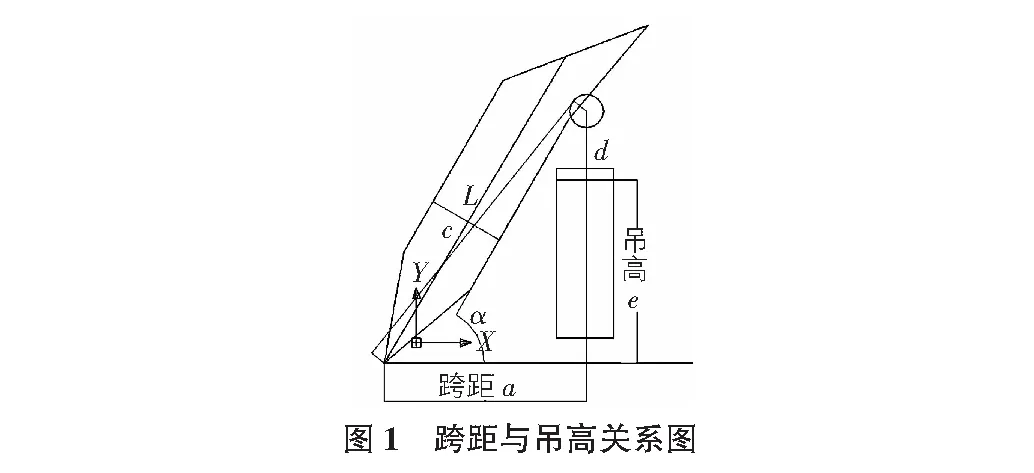
吊高与跨距的关系如图1所示。

2)算法流程。

采用基于粒子群算法改进的蚁群算法，其分析流程如图2所示。

何良诸仿佛遭受重重一击，瘫仰在座椅上，浑身阴溲溲。赵集把他从井下瓦斯禁区背出来，送进小勺酒店，侍候他吃侍候他喝，养息好后，把他送回北大坎市。从此他柳暗花明，步步高升，一去不回头。万万没有想到，他们这样重逢了！

3)设计变量。

根据数学模型，跨距a、吊高e、被吊载物的宽度d是定值，设定吊臂长度L、吊臂高度c和吊臂的仰角α为变量。

4)目标函数。

5)约束条件。

a.应力约束，要求各个杆件的应力均满足条件；b.位移约束，要求跨距达到指定跨距；c.高度约束，要求吊高达到指定吊高。

6)初始目标值见表1。

表1 初始值表

2.2 计算结果

首先研究臂长对吊臂的影响，根据分析结果显示：臂长越长，应力越大，稳定性相应也越差，如图3所示。

其次，研究臂架高度对吊臂的影响，根据分析结果显示：臂架高度越高，应力越小，如图4所示。

最后，看吊臂角度对吊臂的影响，根据分析结果显示，吊臂角度越大，应力越小，如图5所示。

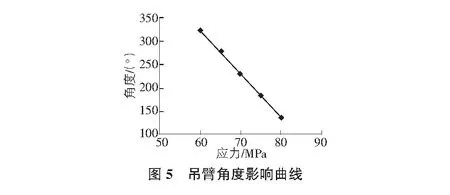
上述曲线也验证了优化的矛盾性，因此对数学模型进行计算优化，计算得到的结果如表2所示。

表2 计算得到的参数

2.3 吊装工况

根据半潜式起重铺管船吊装设计要求，选取如表3所示典型工况进行适应性校核。

表3 吊装工况

通过表4计算结果可以看出，工况三时吊臂与吊载物之间的距离最小，约2.5 m，吊臂与水平面之间的夹角为65°，由于半潜船存在波浪补偿的问题，因此还需要根据需要调整约束条件，即修改主要工况的3.6 m间隙，可调整其他各工况的间隙及角度。

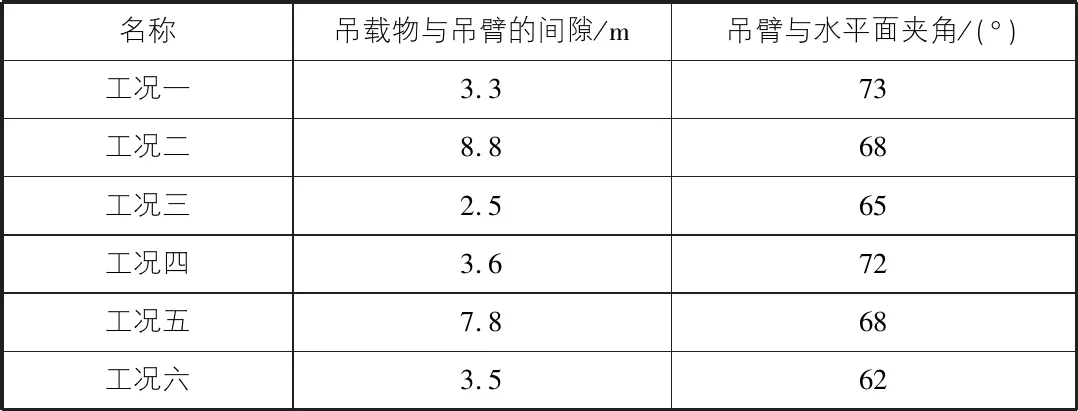
表4 计算结果表

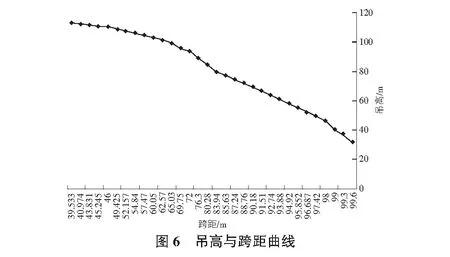
2.4 吊高与跨距关系

根据优化后的吊机扒杆尺寸，计算得到吊机的吊高与跨距关系曲线见图6。经过优化，起吊时吊臂主弦杆正应力最小。

3 研究结论

本文以起吊时吊臂主弦杆正应力最小为优化目标，采用基于粒子群算法改进的蚁群算法对吊机吊高与跨距进行了参数优化，表5为优化前后对比情况。

表5 优化前后对比

由表5可以看出，在保持主弦杆管径660 mm不变的前提下，将吊臂长度、吊臂高度以及吊臂角度都所有提升，同时吊臂管壁厚度也缩减了5 mm，优化后的起重机的吊高与跨距参数能够满足吊装作业工况的设计要求。