曲线线型对公路隧道运营通风影响研究

白 赟 袁 松

(四川省交通勘察设计研究院有限公司，四川 成都 610017)

近年来，随着我国山区高速公路的大力发展，为了提升线路高程、缩短隧道长度和选择合适的洞口，曲线线型越来越多地在隧道平面设计中被采用。但曲线隧道运营通风时的通风阻力明显异于常规直线隧道，而我国公路隧道运营通风的计算与设计仍停留在直线隧道层面上，《公路隧道通风设计细则》关于直线隧道运营通风的计算，对不同曲率的曲线隧道适用性如何，是在隧道通风设计阶段一个亟待解决的问题[1]。

对于公路隧道通风阻力问题，已有很多学者进行了研究。Martegani采用数值模拟方式对隧道侧壁粗糙度与隧道通风阻力之间的关系进行了研究，得到的模拟结果与试验结果吻合度较高[2]；Bener等采用理论公式和CFD模拟相结合的方法对公路隧道洞口局部阻力及局部摩阻损失系数进行了相关研究，经验证，其值与实际情况较为贴合[3]；仇玉良等以秦岭终南山特长公路隧道为工程背景，对喷射混凝土壁面的摩阻损失系数进行了测算与分析，并总结了壁面粗糙度与沿程阻力系数的关系[4]；王亚琼等以茅荆坝隧道的通风斜井为依托，对隧道通风斜井壁面的沿程阻力系数进行了测算并对隧道通风相关计算提出了参考建议[5]；温玉辉采用数值模拟的方法对公路隧道沿程阻力系数进行了模拟分析，并给出了最小值和最大值的取值参考[6]；武义凯基于隧道通风与流体力学的基本理论，采用CFD软件FLUENT进行模拟，得出壁面在不同粗糙单元高度和不同粗糙单元间距下壁面的摩阻损失系数及规律[7]。针对曲线隧道的通风问题，王峰等采用CFD方法对曲线公路隧道的沿程阻力系数及射流风机的布置方式进行了研究，并提出了小半径隧道沿程阻力系数的计算方法[8,9]；芦峰以一半横向通风的曲线公路隧道为研究对象，对曲线型公路隧道的火灾烟气控制进行了数值模拟研究，并探讨了在曲线区域应用射流风机控制烟气的可行性[10]；何佳以干海子曲线公路隧道为工程依托，应用大涡模拟技术，对小半径曲线公路隧道火灾烟气蔓延规律进行了数值模拟研究，并提出了烟气危害的控制方法[11]。通过查阅文献可以发现，国内外学者对于直线公路隧道的通风问题研究较多，关于曲线隧道通风问题有一些研究，但也多是针对曲线公路隧道火灾控烟问题的研究，仅有王峰针对曲线公路隧道沿程阻力系数做了相关研究，并无针对曲线公路隧道较直线隧道通风效率的相关研究。

本文采用流体力学计算软件FLUENT，对不同曲率半径的曲线隧道通风过程进行三维模拟计算，通过对通风过程中曲线隧道内相对通风阻力的对比，探究曲线线型对公路隧道运营通风效率的影响。

1 计算理论

空气在隧道内流动属于非定常湍流流动，而湍流的特点是任一时刻流体内任意点的运动仍然满足连续介质的流动特征，即隧道内流场中所有的空间点满足质量守恒、动量守恒和能量守恒三大方程[12]。各方程表达如下[13,14]：

质量守恒方程为:

(1)

其中，ρ为流体密度；ui为流体在i方向的速度；xi为i方向的坐标。

动量守恒方程为:

(2)

其中，ρ为微元体上的压力；σij为微元体受到的粘性应力；ρgi为i方向的体积力；Fi为污染源、热源等引起的源项。

能量守恒方程为:

(3)

其中:

其中，T为绝对温度；E为单位体积总能，E=CVT，CV为定容比热；K为热传导系数；μ为动力粘性系数；δij为克罗内克符号，当i=j时，δij=1，当i≠j时，δij=0。

2 数值模拟

2.1 计算模型的建立

采用建模软件Gambit建立三维模型，隧道横断面采用高速公路隧道常用的两车道断面(如图1所示)，分别建立曲率半径为600 m，1 200 m，2 400 m的隧道模型，计算模型如图2所示。

2.2 边界条件的设定

隧道壁面和路面设定为壁面(wall)边界条件，隧道入口设定为速度入口(velocity-inlet)边界条件，隧道出口设定为压力出口(pressure-outlet)边界条件[15]。

2.3 模拟工况

为研究曲线线型对隧道通风阻力的影响，分别对曲率半径为600 m，1 200 m，2 400 m和∞(直线)各1 000 m长的隧道进行通风模拟，计算时隧道入口风速取4 m/s。各数值模拟工况见表1。

表1 数值模拟工况

3 模拟结果及分析

分别就隧道内流速场和压力场两方面来分析曲率半径对隧道通风的影响。

3.1 不同曲率半径下隧道流速场分析

不同曲率半径下隧道中部横断面风速分布云图见图3。

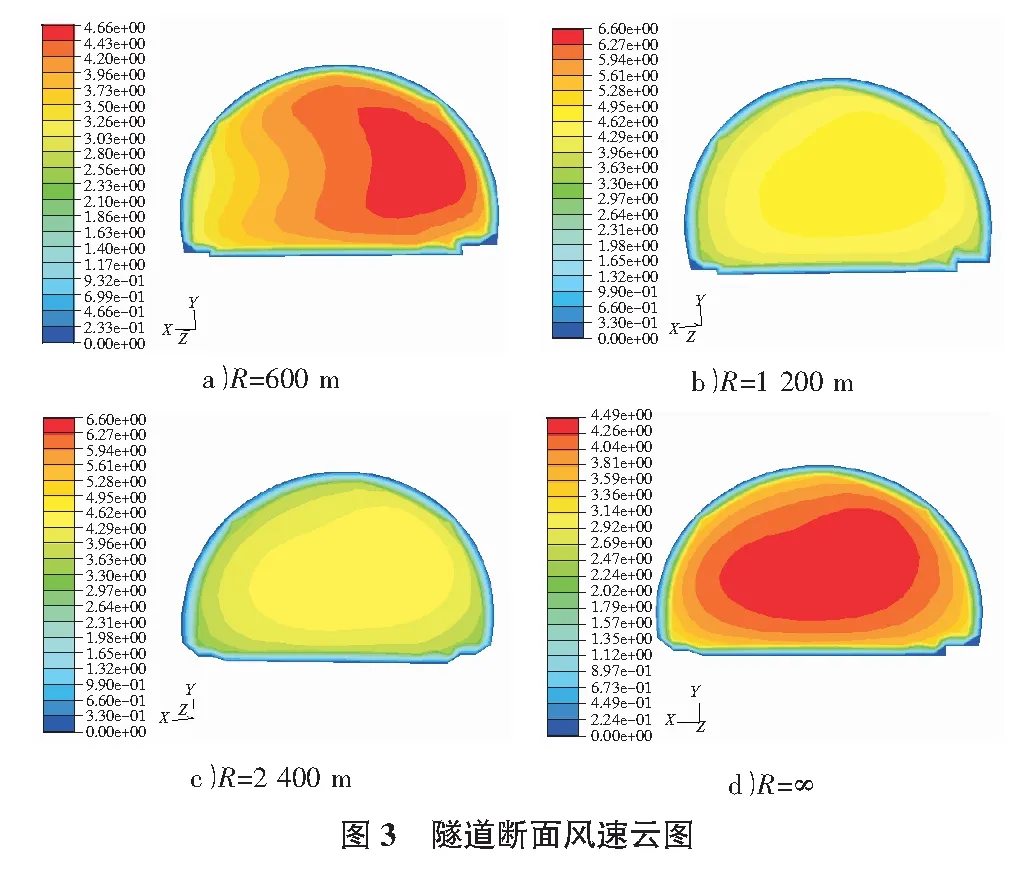
由图3可知，隧道横断面风速受隧道曲线线型的影响，呈现出不对称的特征，相同长度的隧道，曲率半径越小，隧道横断面内风速不对称性越明显，隧道外侧风速越大；当曲率半径为600 m时，隧道内有效风速已偏移到断面外侧1/3区域处。反之，隧道曲率半径越大，隧道中部断面风速分布越均衡，其分布特点越接近直线隧道；当曲率半径为2 400 m时，隧道中部断面风速已接近于直线隧道的分布。

3.2 不同曲率半径下隧道压力场分析

不同曲率半径下隧道中部横断面压力分布云图见图4。

由图4可知，曲线线型影响隧道横断面内压力的分布，相同长度的隧道，曲率半径越小，隧道横断面内压力分布的不对称性越明显，隧道横断面内较大压力区域越往外侧偏移；当曲线半径为600 m时，隧道中部横断面内较大压力分布在断面外侧1/3区域。反之，曲线半径越大，隧道横断面内的压力越接近于对称分布；当曲率半径为2 400 m时，隧道横断面内的压力分布与直线隧道类似，已接近于对称分布。

将隧道出口断面与入口断面的平均压力差视为该隧道的通风压力损失，即通风阻力，并令该值与入口断面初始压力之比为该隧道的相对通风阻力，该值表示隧道通风动力损失率。通过模拟计算结果得到不同曲率半径隧道的相对通风阻力如表2所示。

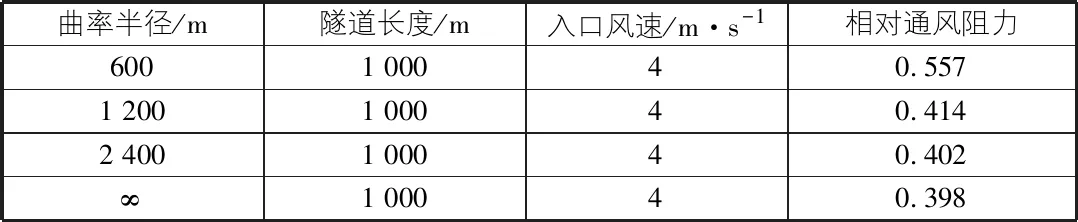
表2 不同曲率半径隧道的相对通风阻力

由表2可知，相同长度的隧道，在入口通风风速相等的情况下，隧道线型的曲率半径越小，隧道的相对通风阻力越大，表明隧道通风动力损失率越大，即隧道通风动力的有效利用率越低；反之，增大隧道线型的曲率半径，隧道通风时可以有效利用通风动力，当曲率半径大于1 200 m时，相对通风阻力与直线隧道较为接近；因此，从隧道通风动力利用率角度考虑，建议曲线隧道的曲率半径不小于1 200 m。

4 结论

本文采用流体力学计算软件FLUENT，计算分析了不同曲率半径对曲线线型隧道通风效果的影响，并就曲率半径、隧道长度和通风风速对曲线隧道通风动力利用率进行了研究，得到如下结论：

1)曲线隧道通风时，曲线线型影响隧道横断面内风速和压力的分布；相同长度的隧道，曲率半径越小，隧道横断面内风速和压力分布的不对称性越明显，隧道横断面内较大的风速和压力区域越往外侧偏移。

2)相同长度的隧道，在入口通风风速相等的情况下，隧道线型的曲率半径越小，隧道的相对通风阻力越大，表明隧道通风动力损失率越大，即隧道通风动力的有效利用率越低；反之，增大隧道线型的曲率半径，隧道通风时可以有效利用通风动力。

3)当曲率半径大于1 200 m时，相对通风阻力与直线隧道较为接近；因此，从隧道通风动力利用率角度考虑，建议曲线隧道的曲率半径不小于1 200 m。