考虑时间影响的桩锚支护深基坑流固耦合分析

周 勇，王 宁，王正振，王延凯

(1. 兰州理工大学甘肃省土木工程防灾减灾重点实验室，兰州 730050； 2. 兰州理工大学西部土木工程防灾减灾教育部工程研究中心，兰州 730050； 3. 兰州理工大学土木工程学院，兰州 730050)

随着中国经济建设的迅猛发展，城市人口越来越多，地下空间的开发和使用变得十分必要，由此产生了大量的深基坑工程。在地下水位比较高的地区，深基坑在开挖前往往需要降水，因开挖卸荷以及降水渗流导致的土体应力、强度、变形等特性的改变已经成为影响基坑开挖稳定性的关键性因素。然而地下水对支护结构的作用机理的理论研究还远落后于实践经验，目前基坑支护设计方法[1]只是考虑了水土合算还是分算问题，而没有考虑到基坑开挖和降水是应力场和渗流场共同作用的过程，因此，深基坑降水开挖很有必要考虑流固耦合效应，基于比奥固结理论运用有限元数值计算方法解决流固耦合问题是目前比较有效的方法[2-7]。

朱彦鹏等[8]运用有限元软件分析了渗流场-应力场耦合作用下的支护结构位移，发现降水与未降水相比，降水工况下基坑总位移大于未降水工况下的总位移。张俏楚等[9]应用三轴试验对基坑开挖与降水交替作用下土体强度和变形进行模拟分析，发现降水能显著减小坑内土体回弹。郑刚等[10]、曾超峰等[11]从基坑开挖前预降水对基坑支护结构变形的影响做了深入研究。刘念武等[12]认为管道沉降和地表沉降的变化趋势相似，且均呈一定的空间效应，管道沉降和土体沉降的差异主要是由于管道具有一定的抗弯能力所致。杨果林等[13]分析了泥炭土深基坑考虑流固耦合时支护结构变形与内力的特点，发现考虑流固耦合时排桩的最大位移和最大弯矩都发生了显著变化。

传统的基坑工程设计是基于瞬态设计的，由于分步降水和逐层开挖是动态性的，所以土体参数也是动态变化的，现分析考虑流固耦合的桩锚支护深基坑变形与支护结构内力随时间的变化，从而对设计施工提出合理性建议。

1 工程背景

1.1 工程概况

1.2 水文地质条件

场地地下水位于地表以下3m处，需要坑内降水，地下水类型包括孔隙潜水和基岩裂隙水。孔隙潜水主要分布在人工填土层，此层透水性好，属于强透水层，裂隙水主要存在于全风化及强风化花岗岩中，风化岩层透水性一般，储水性也较弱。

1.3 基坑支护设计方案

此工程采用桩锚支护，开挖深度为15m，混凝土灌注桩桩径为1 000mm，桩间距为1500mm，桩长为22m，桩嵌固深度为7m，混凝土强度等级为C30，桩顶设置混凝土强度等级为C25的冠梁，桩体外侧挂网喷浆，混凝土面层厚度为100mm，强度等级为C20。预应力锚索采用4排高强钢绞线，锚索钻孔孔径为150mm，具体锚索设计参数如表 1所示，桩锚支护结构剖面图如图 1所示。

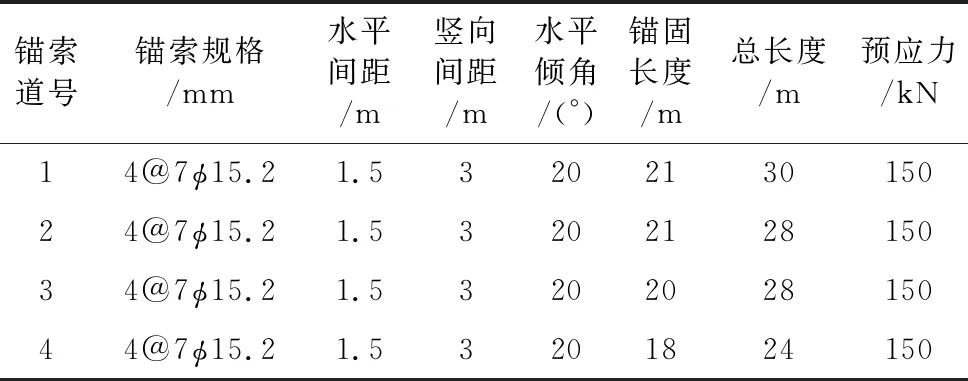
表 1 锚索的设计参数Table1 Design parameters of anchor cable

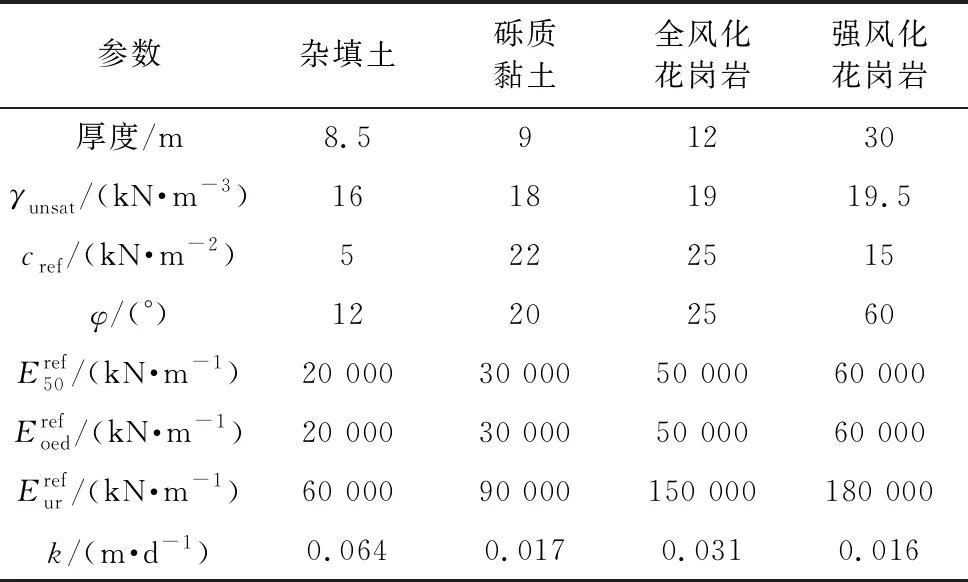
表 2 各土层力学参数Table2 Mechanical parameters of each soil layer

表 3 计算工况Table3 Calculation condition

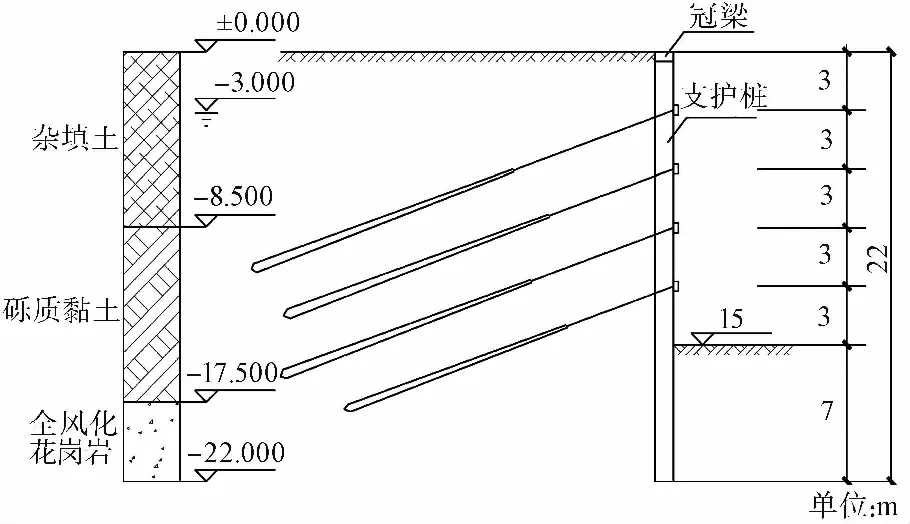
图 1 桩锚支护结构剖面图Fig.1 Cross-section of pile-anchor supporting structure

2 数值模拟

2.1 有限元模型建立

采用岩土软件PLAXIS建立两个有限元模型。其中，一个模型根据工程实际情况考虑流固耦合，在每个开挖步前设定降水步，通过调节水位实现降水，并进行渗流计算；另外一个不考虑流固耦合，初始水位设定为模型底部。并且两个模型都在每个开挖步后设定固结期(未考虑流固耦合的模型设定间隔期)，锚索钻孔及锚索安装、张拉都需要大概10d的时间保证，而这个过程基坑土体固结变形仍在进行，添加固结期或间隔期(设定为10d)来研究时间因素对深基坑变形与内力计算结果的影响，并对二者变形与内力做出对比分析。

表 2 所示为模型具体的土层参数，表 3所示为考虑流固耦合的基坑降水开挖工况，相比而言，未考虑流固耦合的基坑开挖工况仅仅没有降水步。

根据工程经验，此工程问题可简化为平面应变问题，因此，建立二维有限元模型，模型长度为120m，宽度为60m，模型底面采用固定约束，两个侧面边界限制水平位移，上表面设定为自由边界。关于透水性，模型左侧设定为透水边界，右侧边界及底部设为不透水边界。由于基坑降水开挖是个反复加卸载的过程，土体采用土体硬化(hardening soil，HS)模型，考虑流固耦合的模型计算类型均设置为固结计算，以考虑超静水压随时间的变化与消散，未考虑流固耦合的模型设定为塑性变形计算。排桩采用了板单元模拟；锚杆自由段采用点对点锚杆单元；锚杆锚固段采用土工格栅来模拟；支护结构与土体之间采用界面单元分隔开。为不失一般性，在坑外离基坑边缘10m处作用长度为10m，大小为15kN/m的均布荷载，有限元模型如图 2所示。模型建立之后进行单元格划分，总共划分了1247个15节点单元，节点数为10507个，应力点数为14964个，有限元模型网格划分如图 3所示。

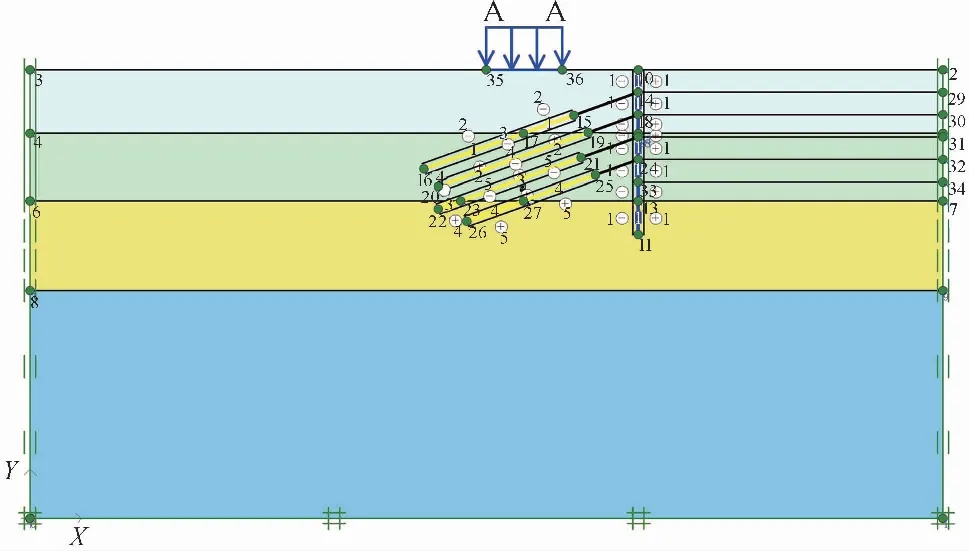
图 2 有限元计算模型Fig.2 Finite element calculation model

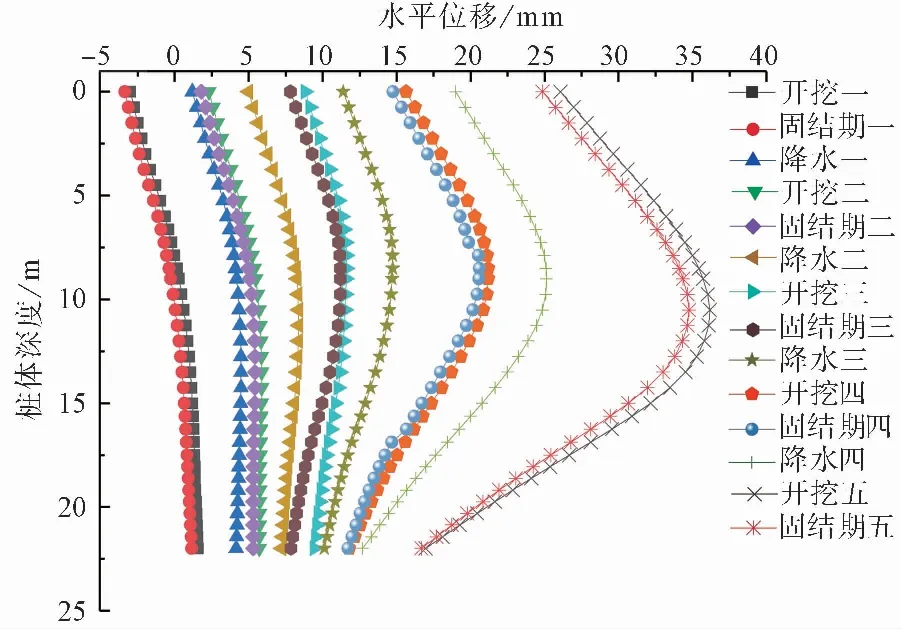
图 4 考虑流固耦合的桩体水平位移Fig.4 Horizontal displacement of pile considering fluid structure coupling

2.2 数值模拟变形分析2.2.1 桩体水平位移

图4 为考虑流固耦合时基坑开挖过程的桩体水平位移曲线。可知，随着开挖深度增加，桩体水平位移不断增大，位移最大值位置也逐渐下移，最终在桩体中部水平位移达到最大，曲线呈现出“鱼腹”状。其中，当开挖深度为3、6、9、12、15m时，桩体水平位移最大值依次为-2.93、5.95、11.68、21.25、36.24mm，需要说明的是开挖一桩体上部负位移的产生是由于开挖后锚索预应力的及时施加导致，因此，开挖后及时安装锚索有利于基坑水平位移的控制。如图4所示，降水过程将会导致明显的桩体水平位移增加，以降水四为例，开挖四的支护桩水平位移最大值为21.25mm，降水四的桩身水平位移最大值增加至25.20mm，可见降水不利于基坑稳定。此外，桩体水平位移表现出较为明显的时间效应，在每一个固结期后支护桩水平位移表现出回缩现象，如固结期五后的水平位移最大值回缩约2mm，这是因为随着时间推移，坑外土体中超静孔隙水压力逐渐消散，土体逐渐固结，并且由于时间变化，渗流导致坑内外水头差逐渐减小，以至于支护桩所受到的水压力也略有减小，最终导致桩体水平位移略有回缩，这有利于基坑安全和稳定。

TNBC由于缺乏有效的靶向治疗位点，尽管患者接受了足剂量的化疗，但仍有30%的患者发生远处转移[5]。到目前为止，研究显示ER和PR可作为乳腺癌的独立预后因子，针对ER和PR的治疗也成为乳腺癌一线内分泌治疗方案，但是女性体内不光有雌激素，还有雄激素，尤其是绝经后的女性，雌激素大量减少了，而雄激素水平却无明显变化。

图5 为不考虑流固耦合与考虑流固耦合的桩体水平位移对比图。

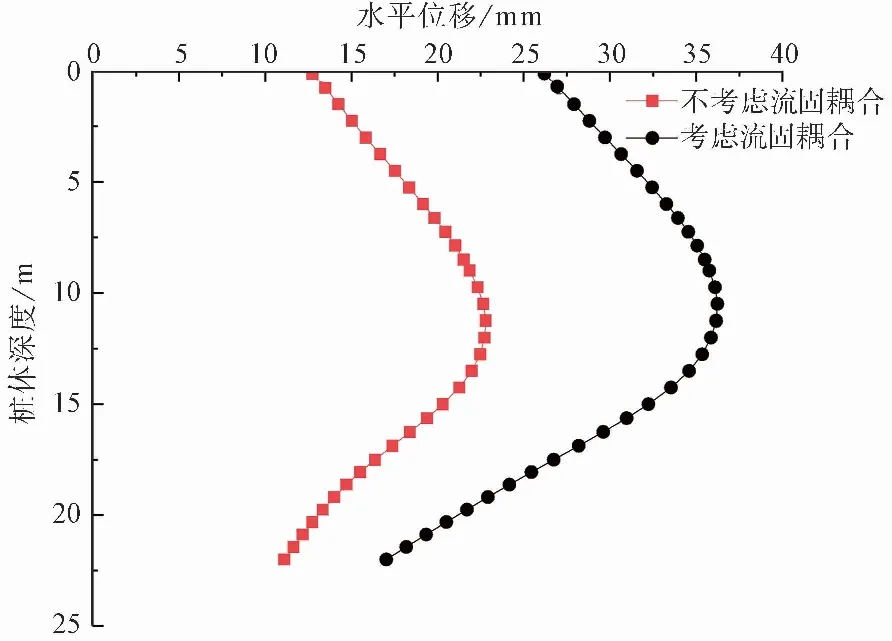
图 5 桩体水平位移对比Fig.5 Pile horizontal displacement comparison

由图5可知，考虑流固耦合与不考虑流固耦合的最终桩体变形规律相似，最大值均出现在桩体中部，上下端变形较小，但考虑流固耦合时的最终桩体变形与不考虑流固耦合的最终桩体变形相比较大。从受力的角度分析可知，考虑流固耦合的桩体不仅受外侧土体的主动土压力，还受到由于坑内外水头差引起的渗流力，所以考虑流固耦合的最终桩体变形整体大于未考虑流固耦合的桩体最终变形，但预应力锚索的及时植入可以将变形控制在允许范围内。

2.2.2 坑外地表沉降

考虑流固耦合的基坑开挖过程坑外沉降曲线如图 6所示，图 7为考虑流固耦合与不考虑流固耦合的坑外地表沉降对比图。

图 6 考虑流固耦合的基坑坑外地表沉降Fig.6 External surface settlement of foundation pit considering fluid structure coupling

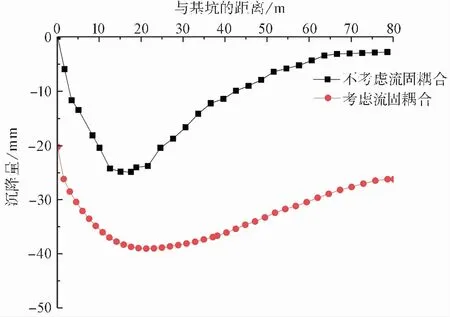
图 7 基坑坑外地表沉降对比Fig.7 Comparison of surface settlement of foundation pit

由图 6 可知，沉降分布曲线整体呈凹槽形，随着开挖深度的不断增加，沉降最大值也快速增大，并且沉降影响范围也不断扩大。开挖结束后，沉降最大值出现在距基坑边1.4H(H为开挖深度)处，最大值为36.5mm。由图可知，降水会导致坑外沉降最大值进一步增大，这是由于地下水位下降形成了降水漏斗，降水漏斗以上的土体逐渐固结，导致有效应力增大，从而使得坑外沉降值增大。同时，可以看到，每个固结步的沉降值均小于每个对应的开挖步，这说明坑外沉降也体现出明显的时间效应。如固结期五坑外沉降回弹现象比较明显，沉降最大值削减了2.66mm，这是由于随着时间推移，坑后降水范围内的土体逐渐固结，负孔压逐渐消散，导致有效应力略有减小，所以土体沉降有所回弹，这反而对基坑安全是有利的。

由图 7可知，考虑流固耦合时的最终沉降量远远大于不考虑流固耦合时的最终沉降量，并且影响范围也更大，由于杂填土土质较差，多次开挖及降水导致坑外80m依然有较大沉降，因此设计方案应充分考虑降水对支护结构及周边环境的影响。这说明降水会使坑外土体沉降明显增大，这对坑外既有建筑及设施的稳定是非常不利的。因此，降水开挖施工过程中加强坑外沉降监测次数十分必要。

2.2.3 坑底隆起

图8 为考虑流固耦合的基坑开挖过程隆起图。

基坑坑底隆起曲线整体呈增长趋势，在靠近支护桩附近隆起曲线斜率较大，随着离支护桩越来越远，曲线渐渐由陡峭变得平缓，并且在基坑对称面处达到最大值。随着基坑逐步开挖，坑底隆起最大值由开挖一的19.12mm增长到开挖五的36.55mm，这是因为，基坑的开挖实质是卸载的过程，卸载后导致土体产生方向向上的回弹。降水会导致土体有效应力增大，即降水可以看作加载过程，由图可知，每个降水步与它所对应的上一个开挖步相比，隆起量明显有所下降，其中，开挖一隆起量最大值为19.12mm，而降水一隆起量最大值下降至9.48mm。基坑坑底隆起也表现出了明显的时间效应，但规律却和坑外沉降及桩体水平位移相反，从图8可以观察到，每个固结期的隆起曲线都在其对应的开挖步隆起曲线之上，这是因为随着时间变化，土体逐渐固结，负孔压慢慢消散，有效应力减小，相当于卸载过程，最终导致固结期后的隆起量大于开挖步，这对坑底隆起稳定性十分不利。

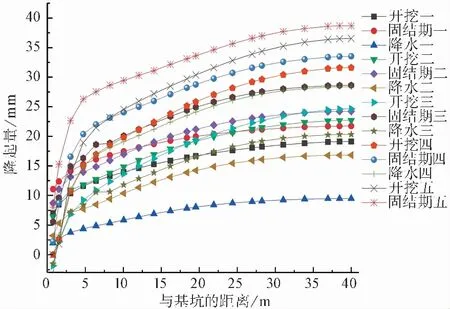
图 8 考虑流固耦合的基坑坑底隆起Fig.8 Uplift of foundation pit bottom considering fluid structure coupling

图9 给出了考虑流固耦合与不考虑流固耦合两种情况下开挖结束后的坑底隆起对比图。

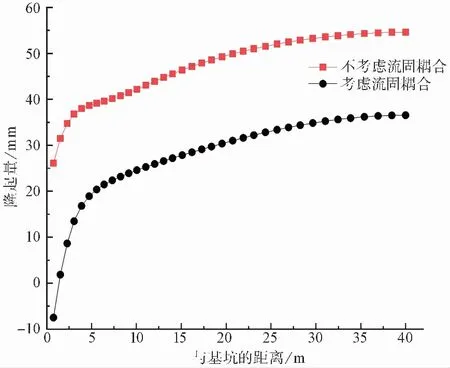
图 9 基坑坑底隆起对比Fig.9 Comparison of uplift at the bottom of foundation pit

由图 9 可知，考虑流固耦合的最终隆起量与不考虑流固耦合的最终隆起量都呈现出随距离基坑侧壁越远，而逐渐增大的趋势，并且两者都在基坑对称面上达到最大值。对比图 9两条隆起曲线大小关系可知，基坑降水对坑底隆起具有明显的削弱作用，这种削弱作用致使考虑流固耦合的基坑底部隆起量总是小于未考虑降水的隆起量。这种规律也能体现在桩体竖向位移上，根据模拟数据，考虑降水时的桩体竖向位移为-25.2mm，不考虑降水时桩体竖向位移为5.4mm。此外，距离支护桩越近，坑底隆起量越小，说明支护结构对基坑底部隆起会产生明显的限制作用。

2.3 考虑流固耦合与不考虑流固耦合的内力对比2.3.1 弯矩对比

图10 所示为考虑流固耦合与不考虑流固耦合两种情况下开挖结束后的桩体弯矩图。

图 10 弯矩对比Fig.10 Moment comparison

比较两种情况的计算结果，可知两条曲线都呈现出相似的变化规律，最大负弯距出现在坑底以下4.2m处，最大正弯矩出现在距桩顶12m处，并且在施作锚杆的位置，弯矩图产生突变。另一方面，考虑流固耦合的弯矩在坑底以上总是大于未考虑流固耦合的弯矩，正弯矩最大值相差64kN·m，在坑底以下规律恰好相反。这是由于降水产生的渗流力在坑外方向是向下的，在坑底方向是向上的，导致坑外土体主动土压力增大[15]，坑内土体被动土压力减小，即降水对土体的应力场产生了影响，导致了弯矩的变化。

2.3.2 轴力分析

表 4为考虑流固耦合与未考虑流固耦合的锚索轴力对比。可知，考虑流固耦合与不考虑流固耦合两种情况下，都是第三道锚索轴力最大，第一道锚索和第四道锚索轴力较小。另外，考虑流固耦合的最终轴力总是小于不考虑流固耦合的轴力，这是由于坑内降水导致坑内外产生水位差，使得坑外地下水位面发生倾斜，而4道锚索的锚固段长度较长，均穿过了倾斜的地下水位面，土体参数发生改变，尤其黏聚力和内摩擦角的变化让锚固段锚固性能有所削弱，导致锚索轴力相对于未考虑流固耦合而言有所下降。这种现象在第一排锚索表现得最为明显，其他三排锚索轴力也有小幅度的下降。

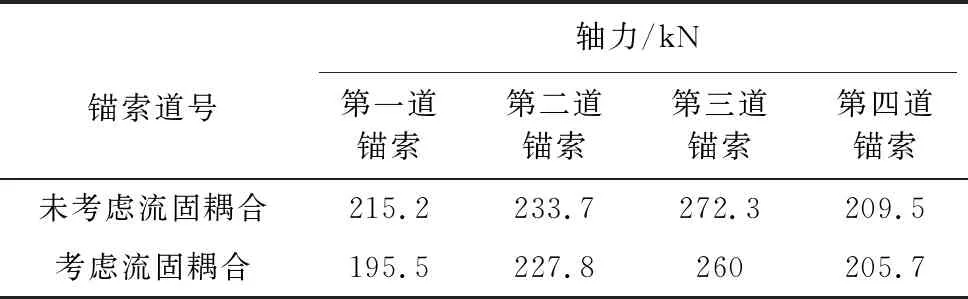
表 4 锚索轴力对比Table4 Axial force comparison of anchor cable

3 结论

(1)在桩锚支护深基坑降水开挖过程中，由于土体中超静孔隙水压力随时间逐渐消散，基坑变形表现出较为明显的时间效应。桩体水平位移和坑外地表沉降在开挖后设置的固结期产生了回弹现象，但固结期的隆起量相对于开挖后有所增大。

(2)考虑流固耦合与未考虑流固耦合计算结果相比，桩体水平位移和坑外地表沉降都明显增长，坑底隆起却明显减小，这说明降水对于坑内隆起稳定性是有利的，对坑外土体和桩体水平位移是不利的。另一方面，由于桩土相互作用，降水对桩体竖向位移和坑底土体隆起有类似的影响，并且桩体对坑底隆起具有削弱作用。

(3)从内力方面进行对比分析，桩体弯矩在坑底以上部分，考虑流固耦合时更大，而坑底以下部分，考虑流固耦合时弯矩却小于未考虑流固耦合时弯矩。另外，考虑流固耦合时的最终轴力小于不考虑流固耦合时的最终轴力，这是因为考虑流固耦合时锚固段穿过了倾斜的地下水位面，土体参数的改变让锚固段锚固性能有所削弱，导致锚索轴力相对于未考虑流固耦合而言有所下降。

(4)经过分析，得出地下水位较高的深基坑支护设计一定要考虑降水渗流带来的影响，这样设计方案才能更加安全。在施工阶段，要充分考虑时间因素对开挖变形的影响，应该在开挖完成后及时施作锚杆(锚索)，并适当增加监测频次，有利于防止基坑变形失控。

(5)有限元数值模型能反映出工程实践规律，是省时省力且比较经济的一种研究方法，但由于地质的复杂性及施工过程的不确定性，数值计算大小仅供参考。