基于MATLAB/Simulink的氢燃料电池系统建模与仿真

张可健, 曲大为, 兰洪星, 于 锋

(吉林大学汽车仿真与控制国家重点实验室，长春130022)

质子交换膜燃料电池具有众多突出的优点，如能量转化率高、能量密度高、噪声低以及零排放等，可以广泛应用于列车、飞机、汽车等交通工具及便携式移动电源等场合[1]。质子交换膜燃料电池系统兼具高效率、高能量密度、高度清洁、大滞后性、非线性、时变性等特点，系统工作过程中涉及电化学、热力学、流体力学、传热传质理论等。目前中外学者建立的燃料电池系统模型主要包括机理模型、经验模型和半经验模型，其中以机理模型居多。

最早的燃料电池建模工作始于20世纪90年代，Springer、Bernardi和Verbrugge等先驱者建立了燃料电池一维模型，提出了解释水分通过膜的机制，并提出了膜电导率与膜中含水量之间的关系，同时对燃料电池的性能进行了初步研究[2]。Zhang等[3]基于建立的燃料电池供气的一维仿真模型，对空气压缩机与燃料电池系统的匹配特性进行了分析，得出设计人员应注重扩展喘振边界，在有限的设计转速下将高效工作区域扩大到低质量流量区域，而不是仅仅扩大有效工作范围的结论。吉林大学雷宗坤[4]基于某电堆设计参数建立燃料供给系统以及输出特性的动态模型，针对特定电流需求条件下的电堆工作点分布与流量-压力特性进行仿真，并基于压力补偿对系统进行控制优化。东北大学马冰心[5]基于系统的机理模型，采用MATLAB/Simulink搭建燃料电池系统仿真平台，围绕燃料电池氧化剂供给控制算法展开研究，通过优化控制器参数得到稳定的系统输出净功率。

针对上述问题，采用单一的建模方法难以准确地得到一个可以描述实际系统的数学模型。现采用机理建模和辨识建模相结合的方式对模型进行推算，反映电堆工作压力、电堆温度、阴阳极工作压力差和氧气过量比等电池运行关键参数的静态和动态响应过程以及绘制出不同工况下电池的输出性能随负载电流的变化曲线图。

1 氢燃料电池输出电压模型

燃料电池可以直接将化学能转化为电能，其理论输出最大电压为热力学理论电动势，即开路电压。但是由于燃料电池自身的结构特点及电化学反应本身，使其存在三项不可逆损失，分别是活化极化电动势、欧姆极化电动势和浓差极化电动势。输出电压模型如图1所示。

正是由于极化现象的存在，使得燃料电池的实际输出电压总是小于理论值，燃料电池实际的输出电压可以表示为热力学理论电动势与极化现象产生的电压损失的差值[6]，即

V=Enernst-Eact-Eohmic-Econ

(1)

式(1)中：V为燃料电池单体的实际输出电压；Enernst为燃料电池单体的热力学理论电动势；Eact为燃料电池单体的活化极化电动势；Eohmic为燃料电池单体的欧姆极化电动势；Econ为燃料电池单体的浓差极化电动势。

在燃料电池输出电压模型的研究中，热力学理论电动势一般由能斯特方程表示，能斯特方程根据阴阳极侧燃料的分压力及温度参数，可以推导出燃料电池单体的热力学理论电动势，又称能斯特电动势，其表达式为

(2)

式(2)中:ΔG为吉布斯自由能，ΔG=237180J/mol；ΔS为标准摩尔熵，由于反应中温度被认为是定值，故熵的变化量近似认为是一个常数，被设为标准值[7]，ΔS=-163.15mol·K；PH2、PO2分别为氢气分压力、氧气分压力，Pa；F为法拉第常数，F=96485C/mol；T为反应过程中的热力学温度，K；T0为参考温度，取为298.15K；R为通用气体常数，取为8.3145J/(mol·K)。

活化极化是一种电极电化学反应迟延造成的电极电位偏离平衡电位的现象，活化极化现象的产生是由于电化学反应过程中，需要消耗能量打破参与反应的物质的化学键，引起了电子的转移，能量的消耗就带来了电压的损失。阴阳极的活化极化电动势由Butler-Volmer表示为

(3)

式(3)中：Eact，a为阳极活化极化过电势；Eact，ca为阴极活化极化过电势；α为电荷传输系数，通常取0.5；i0为交换电流密度，阴阳极两侧的氧化还原反应速度相差较大，交换电流密度也相差较大，通常阴极的交换电流密度要比阳极的交换电流密度低约5个数量级，故活化极化对电池的影响，一般忽略阳极[8]。

欧姆极化损失遵循欧姆定律，且随着电流密度的增大而增大，则欧姆极化损失可以表示为

Eohmic=IRohmic

(4)

式(4)中：I为燃料电池的输出电流；Rohimc为燃料电池单体的内阻，燃料电池单体的内阻主要来自质子交换膜的等效阻抗RM和质子电子转移过程中的阻抗RC，即

Rohmic=RC+RM

(5)

质子交换膜的等效阻抗的表达式为

RM=ρMl/S

(6)

式(6)中:l为质子交换膜的厚度；S为质子交换膜的有效活化面积；ρM为质子交换膜的电阻率，是质子交换膜水含量和电池运行温度的函数，其表达式为

(7)

式(7)中:Tst为燃料电池运行温度；ν为质子交换膜的含水量，仿真膜含水量假设为100%。

浓差极化现象一般发生在高电流密度区域，质子在通过交换膜时，膜附近质子浓度升高，在浓度梯度的作用下，质子向低浓度区域扩散，形成边界层，产生浓差极化电动势。

浓差极化电动势的大小与燃料电池的结构及工作状态相关，其表达式为

(8)

式(8)中：imax为极限电流密度，即所用燃料电池能达到的最大电流密度，一般可以达到2.2A/cm2。

2 氢燃料电池管道模型

氢燃料电池系统模型中，气体管道模型主要包括供给管道模型和返回管道模型。供给燃料经电磁阀流出后进入供给管道，经过加湿器处理后进入电堆，对于空气来说，参与反应之后的废气需通过返回管道排出电堆，对于氢气来说，尾端采取封闭结构，则无气体排出，维持电堆内部参与反应的燃料的分压力及电堆内部的水平衡。质子交换膜燃料电池(proton exchange membrance fuel cell, PEMFC)的阴阳极两侧的供给管道模型基本一致，区别仅为管道内部流体不同，这里仅介绍阴极供给管道模型。

燃料电池供应管道模型指供气管路的集总体积，可以将供气系统从空气入口到电堆阴极所有管路及阀件理解为该模型之中[9]。供气管路中的气体压力变化可以根据质量守恒定律描述为

(9)

式(9)中：Psm为供气管路的压力；Tsm为供气管路中的气体温度，由于供气管路的出口直接进入电堆，故这里用电堆温度来代替供气管路中的气体温度；Vsm为供气管路的集总体积；Matm为入口干空气的摩尔质量；Wsm.in为供给管道入口的空气质量流量；Wsm.out为供给管道出口的空气质量流量。

由于进气管路中的压力与电堆内的压差较小，故可以认为供给管道出口的空气的质量流量与电堆和管道内的压差成线性关系，可表示为

Wsm.out=ksm.out(Psm-Pca)

(10)

式(10)中：Pca为电堆阴极的压力；ksm.out为管道的流量系数。

返回管道即出气管道，反应后的废气经出气管道及尾排阀从电堆排出到大气中。返回管道模型仅对于阴极，对于阳极侧来说，由于采用死端方式，故不对出气管道建模。出气管道模型同供给管道模型类似，根据质量守恒定律，其动态模型可以描述为

(11)

式(11)中：Prm为出气管路的压力；Vrm为出气管路的集总体积；Tst为出气管路中的气体温度，由于出气管路的温度与电堆内的温度相差不大，故这里用电堆温度来代替出气管路中的气体温度；Matm为入口干空气的摩尔质量，Wrm.in为阴极流道出口的空气质量流量；Wrm.out为出气管道出口的空气质量流量。

由于出气管道压力与大气压力值相差较大，故阴极出气管道出口采用非线性的喷嘴方程来确定出口流量大小，即

(12)

式(12)中：CD为管道卸流系数；AT为出口处的截面积；Trm为出气管道内的气体温度，模型中近似为电堆的温度;γ为空气热比率系数；Prm为出气管路的压力；Wrm.out为出气管道出口的空气质量流量。

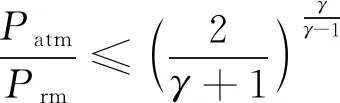
3 氢燃料电池净功率模型

氢燃料电池堆的输出功率可以表示为各个电池单体功率的和，假设电池单体的发电情况基本一致，则燃料电池堆的输出功率可以表示为

Pout=VoutI=nVI

(13)

式(13)中：n为燃料电池堆单体的数目。

在氢燃料电池系统中，一般空气由空压机提供，空压机的能耗来源于燃料电池所产生的能量，氧气过量比越高，则带来的空压机的功耗相应增加，空压机的能耗一般比较高不容忽视。

根据文献[11]可知，空压机等熵功率模型可以表示为

式(14)中：Cp为空气的恒压热容；ηcp为空压机等熵效率；P0为大气压力；γ为空气热比率系数。

净功率模型忽略其他电子附件的能耗，如水泵、电磁阀等，可以表示为系统的输出功率与空压机功率模型的差值，即

Ppure=Pout-Pcp

(15)

根据已搭建完成的氢燃料电池测试系统对建立模型进行模型验证，采集不同工况下的试验数据绘制燃料电池极化曲线，并与仿真结果对比，仿真过程中主要参数如表 1所示。

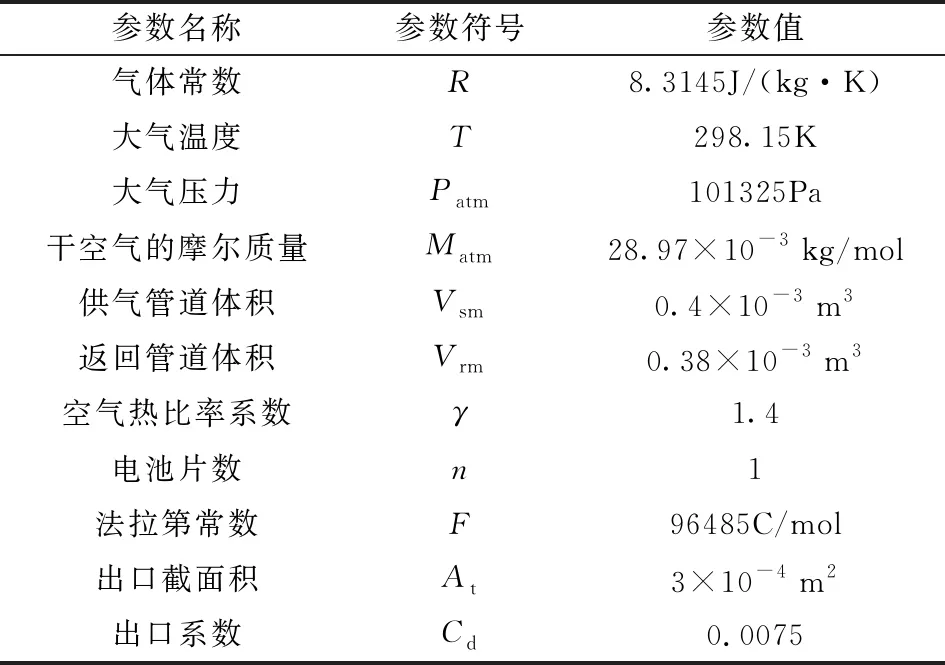
表 1 氢燃料电池系统模型参数Table 1 Hydrogen fuel cell system model parameters

仿真与试验过程中，采用工况为：氧气过氧比为2，环境温度保持25℃，电堆温度保持60℃，阳极侧压力比阴极侧压力高2×104Pa，阳极侧压力随阴极侧压力大小改变，负载电流在0～300A，对应燃料电池电流密度为0～1.2A/cm2。

仿真曲线与试验数据对比如图 2所示。

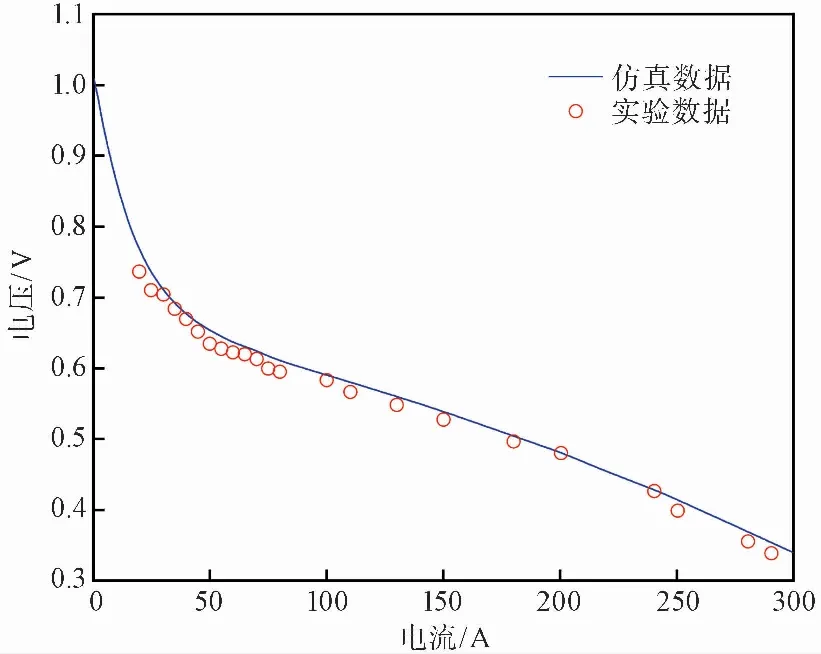
图 2 仿真数据与试验数据对比图Fig.2 Comparison diagram of simulation data and test data

试验数据在极化曲线曲率变化较大区域加密了采样点，燃料电池空载时的开路电压可达1.1V。在低电流密度区域，活化极化的影响显著，由于试验过程中电堆温度分布不均，质子交换膜润湿状况差等因素的影响，电堆内阻增大，试验数据点整体略低于仿真结果；在中间电流密度区域，欧姆极化的影响显著，试验数据点均匀分布在仿真曲线附近，误差较小；在高电流密度区域，因为燃料电池内部水浓度较高，反应生成的水覆盖于催化剂表面不能及时排出，所以浓差极化的影响显著。综上所述，试验数据点的趋势与极化曲线一致，在误差允许范围之内，模型符合燃料电池的运行情况。

4 氢燃料电池系统模型仿真结果分析

4.1 稳态性能分析

4.1.1 阴阳极压差的影响

设置电堆温度为40℃，阴阳极压差分别为0、1×104、2×104Pa。仿真结果如图 3所示。

图 3 不同阴阳极压差下输出电压随负载电流的变化曲线Fig.3 Variation curve of output voltage with load current under different cathode and anode pressure difference

由图 3可以看出，随着负载电流的增大，电堆输出电压在不同的阴阳极压差下性能表现接近，再将曲线局部放大之后，可以看出，在负载电流相同时电堆的输出电压以及输出功率(输出电压曲线与X轴所围成的面积)随着阴阳极压差的增大而增大。这是由于阳极压力高于阴极压力时，在压差的作用下一定程度上促进了水合氢离子从阳极向阴极的迁移，加速了电荷的转移，进而提升了电堆的输出电压以及输出功率。

4.1.2 电堆温度的影响

在研究电堆温度对电堆输出性能的影响时，选择电堆温度分别为40、60、80℃，设置阳极压力高于阴极压力2×104Pa。仿真结果如图 4所示。

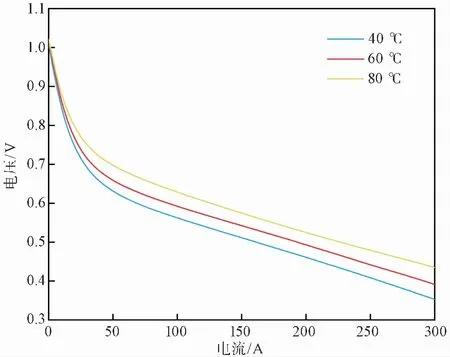
图 4 不同温度下输出电压随负载电流的变化曲线Fig.4 Variation curve of output voltage with load current under different temperature

根据图 4可以看出，随着电堆温度的升高，电池的输出电压逐渐升高，在相同的负载电流下，电堆的输出功率随温度的升高而升高，电堆输出电压以及输出功率的升高率也随着温度的升高而呈上升趋势。这是由于电堆温度升高，可以加快电化学反应中粒子的运动速度，加快氧化还原反应的进程，同时温度的提高可以改善电堆内部加湿条件，有助于质子的迁移，进而提升电堆的输出性能。为了满足实际电堆的要求，电堆的工作温度后续仿真中依然取60℃。

4.1.3 氧气过量比的影响

在氢燃料电池系统工作过程中，氧气过量比可以用来描述供给系统性能的优劣，是PEMFC系统工作过程中的一项重要指标。氧气过量比即为空气供给系统中氧气的供给量与实际电化学反应中消耗的氧气量的比值，可以表示为

(16)

式(16)中:λO2为氧气过量比。氧气过量比越大，一般情况下参与反应的氧气越多，输出电压越高，但是受限于质子交换膜的有效面积，氧气过量比较高的时候，输出电压的增加越来越不明显，同时，氧气过量比越高，空压机的功耗越高，PEMFC系统的净功率就受到影响。当氧气过量比较低时(如小于1)，氧气供应不会造成氧饥饿的现象，对燃料电池造成损伤。一般氧气过量比在2左右比较合适。

仿真过程中，阴阳极压力差为2×104Pa，电堆温度为60℃恒定，负载电流分别为20、40、60、100A。在同一负载电流下，改变氧气过量比，是为了防止发生氧饥饿现象，氧气过量比仿真中最小为1.5，PEMFC系统的净功率随氧气过量比的变化关系如图 5所示。

图 5 PEMFC净功率随氧气过量比的变化曲线Fig.5 Change curve of PEMFC net power with oxygen excess ratio

图5 可以看出，PEMFC系统的净功率随氧气过量比的变化而有波动，变化幅度不是很大。在同一负载电流下，净功率随氧气过量比的增大均先增大后减小，主要是因为随着氧气过量比的增大，供气系统主要是空压机所消耗的能量越多，使得整体的功率下降，在该负载电流下，存在着一个最佳氧气过量比，在此时PEMFC系统净功率最大，且最佳氧气过量比与负载电流相关。负载电流为20A时，最佳氧气过量约比为3.5，负载电流为40A时，最佳氧气过量比约为2.9，负载电流为60A时，最佳氧气过量比约为2.3，负载电流为100A时，最佳氧气过量比约为2.3，可以认为在高电流密度区域内(大于60A)，最佳氧气过量比的值为2.3，而在低电流密度区域(小于60A)，最佳氧气过量比与负载电流呈反比例函数的关系。要保证氢燃料电池堆维持最大有效功率输出，就需要将氧气过量比控制在该负载电流下对应的最佳氧气过量比上。

4.2 动态性能分析

为了研究PEMFC系统的动态特性，设置电堆运行温度为60℃，阴阳极压差为2×104Pa，负载电流的变化如图 6所示，在0～15s，负载电流为150A；在15～25s，负载电流为170A；在25～35s，负载电流为200A；在35～45s，负载电流为180A，在45～55s，负载电流为140A；在55～60s，负载电流为160A。氧气过量比的值如图 7所示，对应的电堆输出电压、输出功率分别如图 8和图 9所示。

图 6 负载电流变化曲线Fig.6 Load current curve

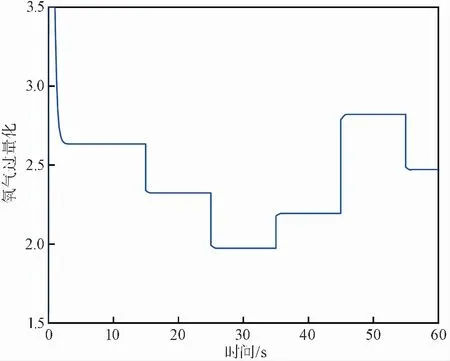
图 7 氧气过量比变化曲线Fig.7 Oxygen excess ratio change curve

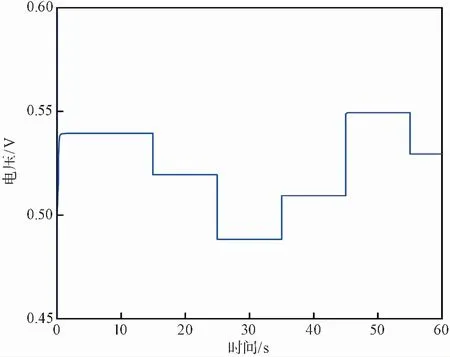
图 8 电堆输出电压变化曲线Fig.8 Stack output voltage change curve

图 9 电堆输出功率变化曲线Fig.9 Stack output power change curve

由图 7的仿真结果可知，负载电流变化时，氧气过量比的大小也随之改变，其变化规律与管路压力以及电堆阴极压力的变化规律类似，负载电流增大时，氧气过量比减小，负载电流减小时，氧气过量比增大，由于响应速度较快，响应速度与负载电流变化的关系不是很明显。

由图 8的仿真结果可知，负载电流变化时，电堆的输出电压随之变化，输出电压的变化规律与氧气过量比的变化规律完全相同。

由图 9的仿真结果可知，负载电流变化时，电堆的输出功率随之变化，输出功率的变化与负载电流的变化呈现出相同的规律，负载电流突然增大时，输出功率比突然增大，负载电流突然减小时，输出功率也突然减小。

由氢燃料电池系统的动态仿真结果可以看出，负载电流的变化会直接影响系统不同位置的压力状态，打破系统压力的平衡点，影响电堆的输出性能。负载电流突然增大时，由电化学反应方程式可知，在供气量不变的情况下，系统所消耗的燃料(氧气和氢气)就越多，导致氧气过量比突然下降，燃料直接消耗的环境压力会突然下降，也就是阴极内部压力会最先下降，而后供给管道压力也下降，负载电流增加得越多，所消耗的氧气就越多，供给系统就越偏离原有平衡点，在压力差的作用下也更快地恢复到一个新的平衡点；负载电流突然增大时，导致参与反应的气体分压突然降低，直接影响了系统的输出电压，致使输出电压降低，尽管输出电压降低，但是降低的幅度相对负载电流来说比较小，系统的输出功率整体依旧是增大。

5 结论

首先对PEMFC系统模型的描述做出合理假设，在此基础上，搭建了PEMFC的输出特性模型、供给管道模型以及净功率模型，其中输出特性模型包括输出电压模型、输出功率模型以及净功率模型，供给管道模型包括氢气供给管道模型和空气管道模型。此外，根据空压机的工作特性，将空压机看作是一个稳定的空气源，通过调节空压机后的电磁阀可以实现空气流量的调节，有效地避免了空压机带来的不利影响，通过净功率模型确立了电堆工作的最佳氧气过量比，该方式大大提高了供给系统的响应速度以及响应时间。

对模型分别进行了稳态仿真和动态仿真研究。稳态仿真主要研究了PEMFC系统的阴阳极压差、阴阳极工作压力、电堆的工作温度以及氧气过量比对电池性能的影响，分析不同工况下关键参数对电池的影响规律；动态仿真为负载电流突变时，得到工况突变时电池的输出性能随时间的变化关系曲线图，分析PEMFC系统进气特性和输出特性的动态响应。根据仿真结果，得出结论如下。

(1)电堆的工作压力、温度、压力差的升高对电堆的输出性能有积极的影响。

(2)氧气过量比的适当增大可以提高电堆的输出性能，但氧气过量比过大时，则会降低氢燃料电池系统的净功率。

搭建的燃料电池模型同样适用于研究不同参数指标的燃料电池系统，具有一定的普适性。根据仿真分析结果确定部分仿真研究的工作参数，为接下来系统控制目标的提出、控制策略的制订奠定了基础。