可重构单驱动3-RRR平面并联机构连杆曲线与姿态的数值解法

李庠，李瑞琴，李辉，宁峰平

(中北大学 机械工程学院，山西 太原 030051)

0 引言

目前，在多工件多位姿的搬运、装配、包装等领域主要采用多驱动的并联机构[1]、串联机构[2]或者连杆机构[3]来实现。多驱动的并联机构由于其正解复杂，导致其控制系统复杂，而单驱动能够简化控制系统，使机构摆脱对传感器的依赖，显著降低连续驱动时的能耗。因此，实现多个精确位姿的单驱动平面并联机构在工程上有重要的应用价值。

3-RRR平面并联机构是典型的平面并联机构，相关文献研究了其运动学和动力学性能[4-8]。Li等[9]研究了3-RRR机构的曲柄存在条件，揭示了该机构的可转动性。Zhang等[10]采用转换驱动模式的方法，在不改变其拓扑结构、不增加冗余的情况下消除平面3-RRR机构的Ⅱ型奇异性。Quintero-Riaza等[11]提出了一种平面并联机构的尺寸综合方法并应用于3-RRR机构，能够优化得到预期的灵巧度好、传动力大、覆盖特定工作区间的机构。

有些学者将平面并联机构约束为连杆机构，进行机构综合分析。Soh等[12]提出由一个平面并联机构约束两个R-R(转动- 转动)的曲柄综合方法，设计出能够实现5个指定位姿的8连杆机构。Chen等[13]通过一个连杆连接两个4连杆，生成一种能够实现11个指定位姿的8连杆机构。Chung[14]提出将两个4杆机构串联起来转化为可以实现17个指定位姿的连杆机构，但该机构具有两个自由度。Surez-Velsquez等[15]提出了一种1自由度的连杆机构，可以实现8个指定的位姿。

Bai等[16]提出的一种通过平行四边形机构约束3-RRR平面并联机构得到1自由度平面并联机构的连杆综合方法，计算得到动平台能够实现10个位姿。但该文献没有对输入- 输出(IO)方程进行求解，必须借助计算机辅助设计(CAD)模型仿真结果确定方程的解属于机构的何种构型，因此还需要进一步研究机构运动轨迹与姿态的求解方法。

在此基础上，本文研究单驱动3-RRR平面并联机构的IO特性，提出一种IO方程的数值解法，利用此方法精确生成机构的连杆曲线(即运动轨迹)和姿态，能够判断在某一输入下得到的多个解分别属于机构的何种构型，摆脱构型分析对CAD模型的依赖；提出一种单驱动3-RRR平面并联机构的重构方法，计算机构重构后的连杆曲线与姿态。

1 3-RRR平面并联机构的数学表示

传统3自由度3-RRR平面并联机构如图1(a)所示，需要3个原动件同时驱动，在通过指定多个位姿的连续运动中，需要传感器实时检测机构的运动位置，驱动电机还需要频繁地进行正/反转的切换，经常进行加速、减速运动，能耗较大，控制系统复杂。为改善以上问题，本文在实验室已有3自由度3-RRR平面并联机构的基础上，提出一种单驱动3-RRR平面并联机构，在实现指定多个位姿的同时，降低软件与硬件成本和能耗。

单驱动3-RRR平面并联机构如图1(b)所示。图1(b)中，Ai、Bi、Ci(i=1，2，3)表示第i个支链的各转动关节，G、H为支链2约束支链1、支链3的转动关节，l1i表示杆BiCi的长度，l2i表示杆AiCi的长度，e1、e2表示动平台A1A2、A2A3的边长，θi0表示第i个支链的初始角度，OBXBYB为固定在B2点的静坐标系。3-RRR平面并联机构有3个原动件，但杆B1C1与B3C3分别被C1G与C3H约束，形成两个平行四边形连杆B1C1GB2和B3C3HB2. 由于杆B1C1、B3C3的转角θ10、θ30分别与B2C2的转角θ20相差θ1-2=θ10-θ20、θ3-2=θ30-θ20，3个角度可以相互表示，故机构自由度为1. 使用θ2j作为输入角θj，其中j表示机构处于第j个姿态：当机构处于初始姿态时j=0；当杆B2C2转过某一角度θ时，会带动B1C1和B3C3同时转过θ角，此时θj=θ20+θ.

图1 3-RRR平面并联机构Fig.1 3-RRR planar parallel mechanism

为了便于描述，将静坐标系固定在B2点，动坐标系固定在动平台的A2点并随之移动，如图2所示。图2中，OAXAYA为固定在A2点的动坐标系，以支链B2C2A2为例，使用向量b2表示B2的位置(由于b2为0向量，故不在图2中标出)，向量a20、c20表示A2、C2的初始位置，向量a120表示初始位姿下A2指向A1的向量。当机构处于第j个位姿时，用向量rj和角度φj描述动平台的位置和姿态，向量a2j、c2j描述A2、C2的位置，a12j表示A2指向A1的向量。支链B1C1A1和支链B3C3A3同理可表示。

图2 机构原动件的初始姿态与第j个姿态Fig.2 Initial orientation and jth orientation of driving link of the mechanism

假设连杆A2C2为刚体，可得

(1)

同理可得关于A1C1与A3C3的方程，故(1)式可写为

(2)

式中：aij=rj+Qjai20；cij=bi+Rjc′i，c′i=ci0-bi；Qj、Rj为平面旋转矩阵，Qj=Q(φj)、Rj=R(θj).

故(2)式可以写为

(3)

(4)

式中：dij=rj+eij，eij=Qjai20-bi.

(4)式简写为

Jicosθj+Kisinθj+Li=0，

(5)

式中：Ji、Ki、Li均为系数，

(6)

(5)式即为机构的综合方程。

2 单驱动3-RRR平面并联机构的IO方程

建立单驱动3-RRR平面并联机构的IO方程，便于研究机构的连杆曲线与姿态，判断机构的构型情况。

图3所示为IO分析的机构运动简图。图3中，μ1为杆A1A2与杆A2C2的夹角，μ2为杆A2C2与杆A2A3的夹角，α为杆A1A2与杆A2A3的夹角，ψ1为杆A2C2与线C1C2的夹角，ψ2为杆A2C2与线C2C3的夹角，σ为线C1C2与线C2C3的夹角，d1、d2分别为C2点到C1点、C3点的距离。

图3 IO分析的机构运动简图Fig.3 Kinematic diagram of the mechanism for IO analysis

对图3所示机构的任一个位姿，使用Freudenstein方程将平面连杆机构的IO方程写成无量纲形式：

k11-k12cosμ1-k13cosψ1+
cosψ1cosμ1-sinψ1sinμ1=0，

(7a)

k21-k22cosμ2-k23cosψ2+
cosψ2cosμ2-sinψ2sinμ2=0，

(7b)

式中：k11、k12、k13为等效4杆机构A1C1C2A2的Freudenstein参数，

(8)

k21、k22、k23为等效4杆机构A2C2C3A3的Freudenstein参数，

(9)

为了方便求解，需要利用输入和输出角度的几何关系减少变量的个数，即

μ1=2π-μ2-α,

(10)

ψ1=2π-ψ2-σ,

(11)

式中：当给定输入角θj后，利用几何关系计算可得σ.通过(10)式、(11)式消除μ1、ψ1两个变量后，(7a)式可重写为

k11-k12cos(μ2+α)-k13cos(ψ2+σ)+
cos(ψ2+σ)cos(μ2+α)-
sin(ψ2+σ)sin(μ2+α)=0,

(12)

(12)式简写为

D1cosψ2+E1sinψ2+F1=0,

(13)

式中：

(14)

同理,(7b)式可写为

D2cosψ2+E2sinψ2+F2=0,

(15)

式中：

(16)

联立(13)式、(15)式，可得

(17)

得到最终的IO方程为

f(μ2)=(E1F2-F1E2)2+(D1F2-D2F1)2-
(D1E2-D2E1)2=0，

(18)

(18)式中只包含一个变量μ2，令t=tan(μ2/2)，利用万能公式

(19)

将(18)式化为一个关于变量t的6次多项式，此时t是可解的。得到t后，μ2和ψ2也能够解出。当解出μ2和ψ2后，A1、A2和A3都能用μ2和ψ2表示，

(20)

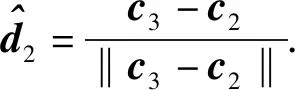
当已知动平台3个顶点中任意2个顶点的位姿时，便可求得rj与φj. 假设已知A1、A2两点的坐标，由图2可知，A1、A3可表示为

a1j=rj+Q(φj)(a10-a20)+a20,

(21a)

a3=rj+Q(φj)(a30-a20)+a20,

(21b)

(21a)式和(21b)式转置后相减，得

(a1j-a3j)T=[Q(φj)(a10-a30)]T=
[cosφj(a10-a30)+sinφjE(a10-a30)]T.

(22)

(22)式等号两边同时右乘E(a10-a30)，得

(23)

(22)式等号两边同时右乘a10-a30，得

(24)

令u=sinφj，v=cosφj，则φj可表示为

(25)

此时，rj可表示为

rj=a1j-a20-Q(φj)(a10-a20).

(26)

由于(18)式为6次多项式，最多具有6个实数解，其每个解都是在机构原动件参数不变情况下的不同构型，即机构除了图1所示的构型外，最多还存在5种不同的构型。

3 单驱动3-RRR平面并联机构的重构方法与IO方程的数值解法

3.1 机构的重构方法

机构重构简图如图4所示。图4中，θRE为重构角度，是B1G1与B1C1的夹角，θRE0为重构后的初始重构角。在杆B1C1的C1点固定一个圆心为B1、半径为B1C1的圆弧形导轨，使G1点能够沿着弧形导轨滑动θRE后固定，以此改变机构的初始重构角θRE0，此时θRE0=θ10+θRE，约束杆B1C1的平行四边形变为B1G1G2B2.θRE每改变一次，则实现对机构的一次重构，每次重构后均可得到一个新的机构。在不同原动件上增加弧形导轨，均能够实现对机构的重构，通过此类方法可以得到若干个新的机构。不失一般性，在此以杆B1C1为例，研究机构重构后连杆曲线的求解方法。

图4 重构的机构运动简图Fig.4 Kinematic diagram of reconfigured mechanism

3.2 机构IO方程的数值解法与重构后IO方程的数值解法

由于建立IO方程时使用了万能公式，采用解析法求解IO方程各个参数时需要进行角度判定，从而增加了解方程的工作量。并且由于(18)式为6次方程，可能存在多个实数解，但无法确定在不同输入角θj下每个实数解之间的对应关系，导致难以求解机构的IO方程，因此本文提出一种IO方程的数值解法。

机构的初始位置如图1(b)所示，以点B2为原点，假设机构各设计参数与运动参数已知。计算(8)式、(9)式，将所得的Freudenstein参数代入(18)式、(19)式求解t.通过(19)式计算得到μ2的所有实数解，即得到机构的所有构型。利用(17)式解出ψ2，代入(20)式计算A1、A2、A3在初始相位角θ10时的值，此时rj与φj均为0，将其作为MATLAB软件中fsovle函数的初值代入(5)式中，计算当θ10转过一个微小角度Δθ后θj的rj与φj，并得到此时A1、A2、A3的值。再将此时的rj与φj作为fsovle函数的初值代入(5)式中，计算θj转过一个微小角度Δθ得到新的输入角θj时机构的rj与φj，得到此时A1、A2、A3的值，以此循环，直到θj=360°时，即可获得机构的连杆曲线。

若已知机构某一位姿，则可将该位姿代入不同构型的方程中(参数t、μ2、ψ2以及动平台初始位姿不同)，检查计算是否收敛，以此判断该位姿属于何种构型，也可判断不同位姿下t的多个解的关系。

当机构重构时只改变了机构的初始重构角θRE0，故上述方法同样适用于重构后的机构。在求解时，只需要改变机构的初始重构角，重复上述方法即可得到机构重构后的连杆曲线，计算流程如图5所示。

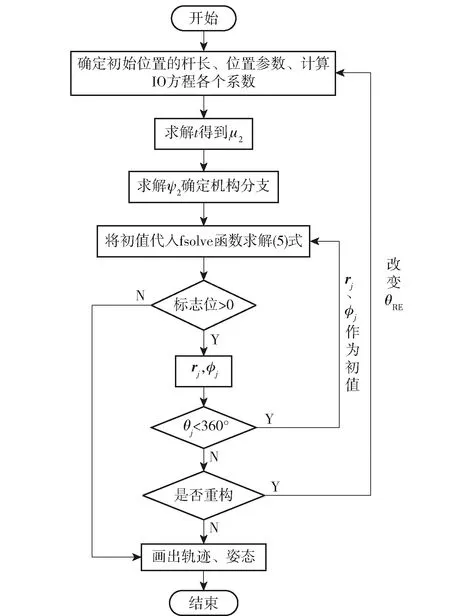
图5 机构连杆曲线计算流程图Fig.5 Flowchart for calculating coupler curve of mechanism

4 数值算例

如图1(b)所示，以点B2为原点，机构的设计参数如表1所示，运动参数如表2所示。

表1 机构的设计参数Tab.1 Design parameters of mechanism

表2 机构的运动参数Tab.2 Kinematic parameters of mechanism

通过(18)式和(19)式计算得到μ2有2个实数解，如表3所示，表明该机构除了图1(b)所示的构型以外，还存在一种构型，如图6所示，即该机构共有两种构型。

表3 IO方程的两个解Tab.3 Two solutions of IO equation

图6 单驱动3-RRR平面并联机构的构型ⅡFig.6 Configuration Ⅱ of single-driven 3-RRR planar parallel mechanism

将图1(b)所示的机构称为构型Ⅰ，图6所示的机构称为构型Ⅱ，构型Ⅰ与构型Ⅱ的设计参数与运动参数完全相同，但动平台A1A2A3的位姿不同。构型Ⅰ的ψ2通过计算所得的值为155.48°，但图1(b)中ψ2明显大于180°，因此ψ2=360°-155.48°=204.52°. 这表明若采用解析法求解IO方程，则还需解决角度判定问题，因此本文提出的数值解法能够很大程度上化简求解IO方程的工作。

构型Ⅰ与构型Ⅱ的重构方法和连杆曲线与姿态的计算步骤相同，因此本文仅以构型Ⅰ作为算例。按照图5所示计算流程计算得到构型Ⅰ的连杆曲线与姿态φj，通过三维建模SolidWorks软件仿真得到连杆曲线，将理论计算曲线与仿真曲线进行比对验证，发现二者完全吻合(以B2为坐标原点、A2为动平台原点)，如图7所示。构型Ⅰ的连杆曲线在x轴上的坐标最大值和最小值分别为50.89 mm和-85.01 mm，跨度为135.9 mm；在y轴上的坐标最大值和最小值分别为102.1 mm和9.76 mm，跨度为111.86 mm.

图7 构型Ⅰ的连杆曲线Fig.7 Coupler curve of configuration Ⅰ

通过动力学仿真ADAMS软件对其姿态φj进行仿真，其仿真结果与理论计算所得姿态的曲线吻合，最大误差约为0.3°，如图8所示。构型Ⅰ的φj在一个转动周期内的最大值和最小值分别为21.67°和-3.91°，跨度为25.58°.

图8 构型Ⅰ的姿态Fig.8 Orientation of configuration Ⅰ

通过仿真结果和理论计算结果的对比，表明IO方程与求解方法的正确性。本文提出方程的求解思路同样适用于其他IO方程求解工作复杂、困难的连杆机构。

机构重构的连杆曲线如图9所示，随着重构角θRE的增加，机构在x轴上的工作范围越来越小，在y轴上的工作范围越来越大。构型Ⅰ在θRE=45°时，连杆曲线在x轴的坐标最大值和最小值分别为25.07 mm和-55.4 mm，跨度为80.47 mm；y轴的坐标最大值和最小值分别为119.6 mm和-7.53 mm，跨度为127.13 mm. 相比于原机构，连杆曲线的工作范围在x轴上减少了40.79%，在y轴上增加了13.65%.由此可得，重构主要影响了构型Ⅰ的连杆曲线在x轴上的工作范围，且θRE每增加15°，连杆曲线在x轴上的坐标最大值减少9 mm左右，坐标最小值增加10 mm左右。

图9 构型Ⅰ重构的连杆曲线Fig.9 Coupler curves of reconfiguration of configuration Ⅰ

由图9(a)可知，重构改变了构型Ⅰ的连杆曲线，但所有重构后的曲线都集中相交于M、N两点附近，在实际应用中可将这两点作为机构的特征点，再通过具体工况选择合适的连杆曲线。

构型Ⅰ重构后的姿态φj如图10所示。由图10可见：随着重构角θRE的增加，构型Ⅰ姿态φj的曲线极值点在横坐标上发生迁移，曲线的大致形状相似，都存在一个波峰和一个波谷，且姿态φj的最大值和最小值也随之增大和减小；当θRE=0°时姿态φj的最大值和最小值分别为21.67°和-14.78°，当θRE=45°时姿态φj的最大值和最小值分别为32.05°和3.911°，最大值和最小值的跨度分别为10.3°和18.691°.

图10 构型Ⅰ重构的姿态Fig.10 Orientation of reconfiguration of configuration Ⅰ

图10(a)中，仿真的姿态φj曲线的个别地方出现局部的峰值，这是因为在仿真过程中该点接近于机构的奇异位置，从而导致机构运动的突变。由于奇异位置的存在也限制了仿真过程中仿真步长的设置，最终导致姿态φj局部峰值的出现，与理论结果出现差异，因此在之后的研究中还要对机构的性能进行分析与优化。

由图9、图10可知，构型Ⅰ通过理论计算得到连杆曲线与姿态φj都与仿真结果相符，表明本文所提IO方程数值求解方法的正确性，并能够适用于重构后机构的计算。

5 结论

本文利用Freudenstein方程推导出单驱动3-RRR平面并联机构的IO方程，提出一种数值求解方法。在此基础上，提出了一种通过改变某一驱动转动副的初始角度实现重构的方法并通过数算例求解验证。得到以下主要结论：

1)提出一种IO方程的数值解法，得到机构的所有构型及其连杆曲线与姿态，能够通过计算判断某一位姿属于机构的何种构型。

2)通过对比理论与仿真得到的连杆曲线与姿态φj的曲线，证明该数值求解方法的正确性。该方法化简之后的构型分析工作，可为其他求解IO方程工作复杂、困难的连杆机构提供参考。

3)使用提出的求解方法计算了该可重构机构的运动轨迹，理论计算结果与仿真轨迹相符，证明了该方法同样适用于重构后的单驱动3-RRR平面并联机构。

4)提出的约束方法能为其他多驱动平面并联机构转化为单驱动或少驱动机构提供研究基础；采用的重构方法可为单驱动机构改变运动轨迹的重构设计提供参考。

参考文献(References)

[1] 李建钢，杨桂林，张林，等.基于柔性并联机构的变刚度夹持器设计分析[J].机械工程学报，2019，55(21):64-72.

LI J G,YANG G L,ZHANG L,et al.Design analysis of a variable stiffness gripper based on flexible parallel mechanism[J].Journal of Mechanical Engineering,2019,55(21):64-72.(in Chinese)

[2] 郑昱，广晨汉，李前，等.一种新型物料装填机器人的设计与轨迹优化[J].兵工学报，2020，41(4):763-770.

ZHENG Y,GUANG C H,LI Q,et al.Design and trajectory optimization of an object loading robot[J].Acta Armamentarii,2020,41(4):763-770.(in Chinese)

[3] 彭京徽，王德石，张弘弨.舰炮含钳爪回转机构的伸爪运动特性研究[J].兵工学报，2020，41(5):874-880.

PENG J H,WANG D S,ZHANG H C.Research on the motion characteristics of extendable gripper of rotary conveyor mechanism in naval gun[J].Acta Armamentarii,2020,41(5):874-880.(in Chinese)

[4] CAN E,STACHEL H.A planar parallel 3-RRR robot with synchronously driven cranks[J].Mechanism and Machine Theory,2014,79:29-45.

[6] LIU S,QIU Z C,ZHANG X M.Singularity and path-planning with the working mode conversion of a 3-DOF 3-RRR planar parallel manipulator[J].Mechanism and Machine Theory,2017,107:166-182.

[7] WU X Y,BAI S P.Analytical determination of shape singularities for three types of parallel manipulators[J].Mechanism and Machine Theory,2020,149:103812.

[8] ZHANG X C,ZHANG X M.A comparative study of planar 3-RRR and 4-RRR mechanisms with joint clearances[J].Robotics and Computer-Integrated Manufacturing,2016,40:24-33.

[9] LI R Q,DAI J S.Crank conditions and rotatability of 3-RRR planar parallel mechanisms[J].Science China-Technological Sciences,2009,52(12):3601-3612.

[10] ZHANG Z K,WANG L P,SHAO Z F.Improving the kinematic performance of a planar 3-RRR parallel manipulator through actuation mode conversion[J].Mechanism and Machine Theory,2018,130:86-108.

[12] SOH G S,YING F T.Dimensional synthesis of planar eight-bar linkages based on a parallel robot with a prismatic base joint[C]∥Proceedings of the ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.Portland,OR,US:ASME,2013.

[13] CHEN C,ANGELES J.A novel family of linkages for advanced motion synthesis[J].Mechanism and Machine Theory,2008,43(7):882-890.

[14] CHUNG W Y.Synthesis of two four-bar in series for body gui-dance[J].MATEC Web of Conferences,2017,95:04006.

[16] BAI S P，LI Z Y，LI R Q.Exact synthesis and input-output analysis of 1-DOF planar linkages for visiting 10 poses[J].Mechanism and Machine Theory,2020,143:103625.