舰船纵摇突变对舰面流场的影响
李 通,王逸斌,赵 宁
(南京航空航天大学 非定常空气动力学与流动控制工业和信息化部重点实验室,南京 210016)
0 引 言
近年来,我国各种先进的作战舰艇陆续下水服役,第一艘航母“辽宁舰”和第二艘航母“山东舰”分别于2012年和2019年交付海军,近两年我国的大型驱逐舰和两栖攻击舰也相继下水。这些舰艇的抛头露面,使得海军武器装备体系逐步现代化和完备化,其中舰载机已经成为了必不可少的配套作战装备。舰船甲板是舰载机于海上作业的主要起降场地,而甲板上的流场受海面自然风、岛式上层建筑与舰船运动综合影响,当舰船运动或者有风时,上层建筑后方会产生不均匀的尾流场,常伴随有分离、回流、旋涡等运动形式的发生。例如当舰载直升机在甲板上进行起降作业时,旋翼与舰船之间会形成复杂的混合涡流区,使得飞行甲板上方的飞行作业变得极具危险性。所以必须首先对舰船飞行甲板上方的空气流场特性有一个清楚的认识。
早期舰面流场研究主要采用实船测量和风洞实验两种手段。2000年,国内南京航空航天大学的顾蕴松等[1]使用七孔探针三维流场测试设备,对实际航行中的某驱逐舰舰尾飞行甲板流场进行实测,给出了飞行甲板直升机起降区域流场的速度矢量图。2007年,赵维义等[2]通过某型舰船模型风洞实验的PIV结果,介绍了舰船尾流场特性,指出尾流场中下冲气流和涡流区对直升机的影响最大。随着近年来计算机技术的迅猛发展,计算流体力学(CFD)数值模拟手段得到逐步完善与发展,并被广泛应用到舰面流场的研究中。Polsky和Woodson分别对LHA级美国海军舰船和海军驱逐舰DDG-81周围的非定常流场进行了数值模拟计算,为CFD方法成功应用于舰面流场模拟提供了依据[3-4]。郜冶等[5]通过数值模拟研究了舰载机滑跃起飞过程对舰面气流分布的影响,之后他们在美国CVN级航母上进行了风向变化对甲板涡结构特征影响的研究[6]。2009年洪伟宏等[7]研究发现减少上层建筑尺寸可以较明显地改善上层建筑附近区域的舰船空气流场特性。陆超等[8]认为风向角的变化对舰船舰面空气流场的形态有较大影响,且越靠近上层建筑区域气流变化越剧烈。2012年赵永振[9]计算了舰船在艏摇运动状态下,飞行甲板上方的非定常空气流场,但是计算周期较短,没有给出流场变化的周期性。2014年,刘长猛等[10]发现在0°风向角时,机库门敞开有助于改善飞行甲板的气流场状况。还有学者采用分离涡模拟方法对舰面流场进行了不同方面的数值研究[11-13],捕捉到了舰船尾流场中较为精细的涡结构。近两年,中国船舶工业系统工程研究院的许多学者在舰面流场方面也做了大量的研究[14-19]。其中赵鹏程和李海旭等研究了直升机舰上起降安全的影响因素,指出了空气流场特性参数对舰载直升机的影响[14]。宗昆等使用“作用盘方法”和“运动嵌套网格”方法对舰载直升机起降区空气流场进行了对比研究[16]。王金玲和姜广文等研究了甲板风和大气边界层对舰船空气尾流的影响,认为0°~15°的风向角范围适合舰载直升机的起降作业[17-18]。高杰等通过主动控制技术,改善了航母的公鸡尾流环境[19]。国外学者Watson等[20]在2019年对英国新航母伊丽莎白女王号上的非定常气流进行了数值计算和实验建模研究,发现在斜风状态下,该航母的双舰岛结构会导致飞行甲板上产生更加复杂的气流。
目前大多数舰面流场的研究都是在舰船静止的状态下进行的,而在真实海况下,舰船会产生不同程度的横摇、纵摇、艏摇、横荡、纵荡和垂荡,这些随机运动使甲板上方的流场更加复杂,可能会严重影响到舰载直升机的起降安全。然而国内有关舰船在摇摆状态下舰面流场特性的研究相对较少,特别是海浪随机性造成的摇摆参数突变对舰面流场带来的重要影响。因此,本文基于两栖攻击舰的简化模型,使用CFD方法对不同纵摇状态下的舰面流场进行数值模拟研究,在舰船最大纵摇角度和纵摇周期突变的情况下,对舰面流场特性的变化做了进一步的分析和总结,进而得到舰船纵摇突变对飞行甲板上方流场的影响,为舰载机的甲板作业提供一定安全参考。
1 数值方法及验证
1.1 控制方程和计算方法
由于舰船甲板上方的流动为低速不可压流动,所以给出不可压流动的控制方程:
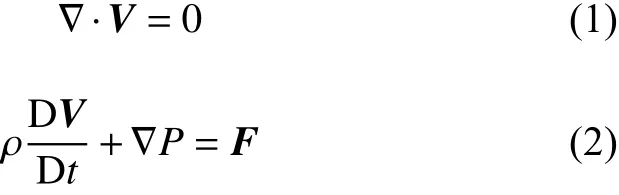
式(1)为连续方程,其中V为速度矢量。式(2)为动量方程,其中D/Dt为物质导数,描述运动流体微团的某个量随时间的变化率,ρ为流体的密度,P为流体所受的压强大小,F为黏性力矢量。使用Fluent软件对流场进行非定常数值计算,采用雷诺平均方法中的k-ϵ湍流模型来封闭方程,同时选择基于压力的SIMPLE(Semi-Implicit Method for Pressure-Linked Equation)算法进行计算。
对于纵摇运动的实现,采用动网格方法,在定义边界运动时,利用Fluent自带的UDF (User Defined Function)功能对运动区域的运动方式进行指定,网格更新采用弹簧光顺法和网格重构法。在弹簧光顺方法中,网格被理想化为节点间相互连接的弹簧,根据胡克定律可以得到网格节点的弹簧力:

其中 Δxi和 Δxj分别为节点i与节点j在形变作用下发生的位移,ni为 与节点i相连的节点数量,kij为节点i与节点j之间的弹簧刚度,定义如下:

其中kfac为弹簧因子,在本文中取0.5。
当处于平衡状态时,与节点i相连接的所有弹簧力的合力为0,可以得到如下迭代计算:

其中m为迭代数,在本文中取30。当迭代计算收敛后,节点i的位置通过下式更新:
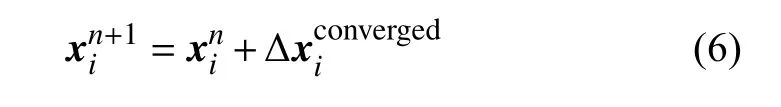
1.2 计算方法验证
为了建立一个舰船尾流验证数据库,国外提供了高度简化的护卫舰外形(SFS)几何结构模型[11,21],图1中给出了SFS和更新版本SFS2。为了验证SFS/SFS2预测真实护卫舰飞行甲板上方流场的可靠性,许多学者利用不同的计算方法对SFS/SFS2的舰面流场进行了一系列的数值模拟研究[22-28]。
本文对SFS2模型周围的流场进行了数值计算,并将结果与实验数据及其他文献的计算结果进行了比较[11,26]。在SFS2甲板上方取一横向观测线,该观测线平行于甲板表面,长度为甲板宽度的两倍,其在垂直方向上的投影位于甲板中心。图2给出了观测线上的速度分布曲线的对比。其中y表示观测线上的点到甲板中心的距离,已用甲板宽度b无量纲化;u、v、w分别表示流向速度、横向速度和垂向速度,已用来流速度V∞无量纲化。通过对比可以看出本文的数值计算结果与Li等的计算结果较为吻合。数值计算得到的横向速度和垂向速度分布与实验结果基本一致,而甲板中心处的流向速度与实验结果存在一定偏差,造成这种差异的原因是流动经过机库后会发生流动分离现象,且在机库后方形成紊乱的涡流区,导致占主导地位的流向速度变化剧烈,而湍流脉动量被RANS模型平均化,不能较好地捕捉到这种变化。但是总体上本文的计算结果和其他学者的研究结果比较吻合,且本研究主要关注垂向速度的变化,所以该方法可以满足研究需求。

图1 SFS2模型示意图(SFS模型用深灰色表示)[11]Fig. 1 Schematic of SFS2 model (SFS model is shown in dark shading)[11]

图2 实验数据和数值计算结果的对比Fig. 2 Comparison between the experimental data and numerical simulation results
为了进一步验证RANS方法对舰船运动流场数值模拟的准确性,图3给出了舰船以式(7)进行纵摇运动时的RANS和DES数值计算结果对比,采用的舰船模型如图4所示,其中1#~4#表示舰载直升机在甲板上的4个起降位置。各选取1#和4#起降位置上方10 m高度的两个观测点,得到了无量纲垂向速度随时间的变化曲线。对于舰首的1#位置,受涡流影响较小,所以两种方法得到的曲线比较光滑且相吻合,但是舰尾4#位置由于受到脱落的舰首涡和上层建筑尾涡的严重影响,导致速度波动比较大,RANS未能很好的捕捉到这种波动,但是整体的变化趋势和DES结果较为一致。从表1中也可观察到两种方法得到的垂向速度平均值(AVE)和标准差(STD)较为接近。因此,可以认为RANS方法能够满足本文的研究需求。

图3 DES和RANS结果的对比Fig. 3 Comparison of the DES and RANS results

图4 舰船模型示意图Fig. 4 Schematic of the ship model

表1 不同数值方法下垂向速度的平均值和标准差Table 1 Mean and standard deviation of vertical velocity computed from different methods
2 计算模型与网格
所用两栖攻击舰简化模型如图4所示,甲板上4个白点作为舰载直升机起降位置,从舰首至舰尾依次编号为1#~4#,其中1#位于舰首,2#和3#位于上层建筑左侧,4#位于舰尾。整个流场的计算域为长方体,如图5中的黄色区域所示,舰船正前方为速度入口边界,后方为压力出口边界,上下为对称边界,当正向来流时,舰船左右侧为对称边界。绿色长方体为运动区域,随舰船一起做纵摇运动,蓝色长方体为舰船周围加密区域。计算的网格采用非结构网格。图6为经过上层建筑的截面网格,总的网格单元数量大约为1 300万。
在真实海况下,由于海浪的随机性,舰船的摇摆情况比较复杂,一般为不规则的运动,但是已有学者将舰船摇摆运动假设为简谐运动,进行直升机/舰组合风限图计算方法的研究[29-30],因此本文为舰船纵摇建立简谐运动模型,其运动方程为:

其中 ωy表示舰船绕y轴转动的角速度,单位为rad/s(1 rad = 57.296°);A表示最大角速度,单位为rad/s;t和T分别表示任意时刻和纵摇周期,单位为s;θ为初相。图6中的红点表示纵摇中心,α表示纵摇角。
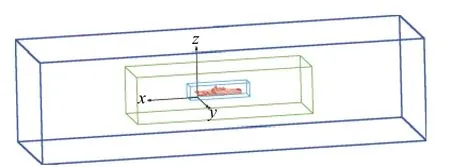
图5 流场区域示意图Fig. 5 Schematic of the flow field
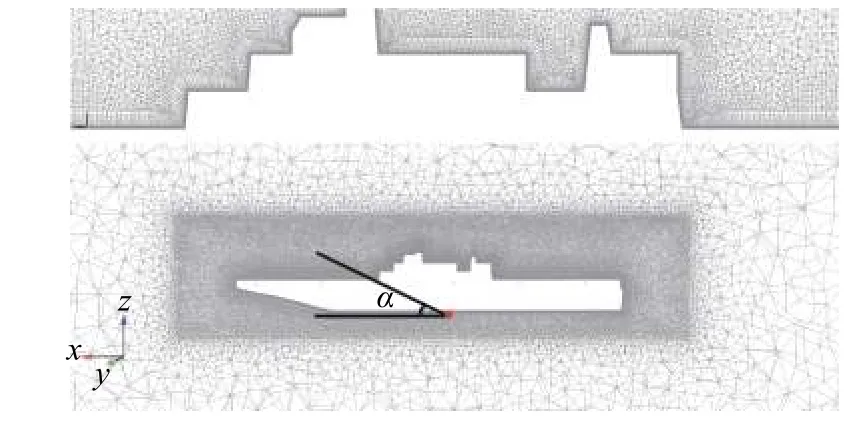
图6 经过上层建筑的截面网格Fig. 6 Section grid cutting through the superstructure
3 结果与分析
首先在初始周期和振幅的纵摇状态下,对舰面流场进行了数值模拟,给出甲板上方流场结构的变化情况。然后在初始纵摇状态下,将纵摇周期和振幅减半,对舰面流场的变化做了进一步的分析和总结。为了观察流场中垂向速度大小的变化,分别选取4个起降位置上方10 m高度处的观测点,如图7中所标示。

图7 甲板上方观测点位置示意图Fig. 7 Schematic of observation points over the deck
3.1 纵摇状态下的流场结构
对于初始的纵摇运动状态,取A= 0.01 rad/s,T=20 s, θ=0,则运动方程表示为:
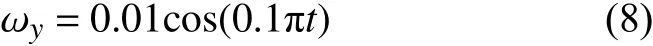
通过对式(8)从0到1/4周期积分可以得到纵摇角度的最大值(振幅)为1.82°,数值模拟的来流风向角为0°,即顶风来流。
图8为流场中的涡结构分布图,用 λ2< 0时的等值体图来表示。 λ2是 一种描述涡量的方法[31],当 λ2< 0时表示流场中有涡存在,从中可以很直观的呈现出流场中的四种涡结构,包括舰首涡、边缘分离涡、上层建筑尾涡和舰尾涡,分别用A、B、C、D表示。图中用垂向速度着色,红色区域为上洗流区域,蓝色区域为下洗流区域。

图8 涡结构分布图Fig. 8 Distribution of vortex structures
图9给出了舰船在一个纵摇周期中,甲板上方的涡结构在不同时刻的发展情况。受船体前缘钝体效应作用,来流经过舰首的尖锐边缘后,发生了较大范围的流动分离,在舰首位置形成了类似于梯形的舰首涡。随着时间的变化,舰首涡在甲板中心发展成一系列涡圈,离开舰首后沿甲板向后运动,途中受上层建筑及其尾涡影响,涡圈发生形变,破坏了其完整性,最后从舰尾脱落并和舰尾涡混杂在一起。在一个纵摇周期中,涡圈经历了从生成到发展再到脱落的过程,且会经过甲板上各个观测点,这对直升机在该位置的起降作业有一定的影响。来流在舰船两侧分别形成两条旋转方向相反的边缘分离涡,由舷外转向甲板,并在顺着来流向后发展的过程中,与舰尾涡混合在一起,然后从舰尾脱落。由于该涡系影响的甲板面较小,位置主要位于甲板左右两个边缘附近,且高度较低,所以对舰载直升机起降影响较小。来流绕过上层建筑后在背风侧发生了流动分离,进而形成上层建筑尾涡,该尾涡的主要特征为左右交错的两列涡圈,随着时间的变化向后运动并逐渐膨胀,直至破碎后从舰尾脱落。舰尾是类似于后台阶的结构,流动在舰尾再次发生了流动分离,产生了涡流区,并伴随着复杂的涡结构,即舰尾涡。
图10给出了6个纵摇周期中,甲板上方10 m高度处观测点的无量纲垂向速度变化曲线图。在第0 s时,舰船由静止状态突然开始纵摇,甲板上方的流场受到突然扰动。在运动前期,流场正在建立,处于不稳定状态。从80 s之后的垂向速度变化曲线来看,在顶风来流状态下,4个观测点处的垂向速度随时间基本呈周期性变化,周期约为20 s,即舰船纵摇运动的一个周期。同时,在一个纵摇周期中,4个观测点都会受到上洗流和下洗流的交错影响。但不同位置处的垂向速度的大小和变化趋势有着明显的不同。

图9 不同相位的涡结构分布图Fig. 9 Distribution of vortex structures at different phases

图10 甲板上方观测点的无量纲垂向速度变化曲线图Fig. 10 Variation of dimensionless vertical velocity at observation positions over the deck
从第二个周期开始,1#位置的垂向速度曲线图基本呈周期性,而其他三个位置的垂向速度峰值有继续扩大的趋势,2#和3#位置的垂向速度在第三个周期开始出现周期性变化,4#位置的垂向速度直到第五个周期开始才呈现出周期性变化,说明当舰船从静止状态开始进行周期性纵摇时,位于甲板上方不同位置的周期性流动不是同步建立的。这是因为顺着来流的方向,流场首先在舰首趋于稳定,位于舰首处1#位置的周期性流动在第二个纵摇周期就基本建立起来,而2#和3#位置处于上层建筑的左侧,4#位置处于舰尾附近,这三个位置受到不断脱落的舰首涡和上层建筑尾涡两种涡系的混合干扰,进一步影响流动的周期性,所以这三个位置直到第五个周期开始才都建立起有规律的周期流动,滞后于舰首的1#位置。
为了进一步分析各观测点的垂向速度在纵摇突变后的波动情况,图11给出了不同时间段的垂向速度标准差,其中第0个周期段表示舰船处于静止状态,第1个周期段表示开始纵摇的第一个周期,以此类推。可以发现,从静止状态到纵摇状态,各位置垂向速度有明显的波动,在纵摇的第一个周期中,位于舰首的1#位置的波动最大,在第二个周期中略微减小,随后基本保持不变,说明该位置的流动已经建立起周期性。对于2#位置,垂向速度的波动明显先减小后增大,并在第三个周期后基本保持不变,而3#位置的垂向速度的波动在纵摇的前三个周期一直增大,之后才保持不变,说明2#和3#位置的流动从第三个纵摇周期开始建立起周期性。对于4#位置,垂向速度的波动直到第五个纵摇周期才开始保持不变。这些结果与图10的结果是一致的。对于舰载直升机在甲板上是否能够安全起降,在国际上的判定标准为CAP 437标准[32],规定当甲板上方垂向速度的标准差低于1.75 m/s时才可进行起降作业,否则可能会导致安全事故。从图11中可以看出,各位置在纵摇过程中的垂向速度标准差都小于1.75 m/s,因此舰载机在当前纵摇环境下进行甲板作业相对比较安全。

图11 不同周期段的垂向速度标准差Fig. 11 Standard deviation of vertical velocity at different periods
在4个起降位置上方的不同高度各自再取3个观测点,分别距甲板表面高5 m、15 m和20 m。图12给出了在不同高度处,最后一个运动周期的垂向速度标准差,从中分析在纵摇状态下不同高度处垂向速度的波动情况。通过对比发现,随着高度的增加,1#位置处垂向速度的标准差有明显的减小,而其他三个位置的垂向速度标准差的变化并不明显,仅有微弱的增加或减小。由于1#位置位于舰首附近,其流场受纵摇运动的影响比较大,而且在较低位置还会受到舰首涡脱落出的涡圈的影响,导致在5 m高度时,其垂向速度的标准差相对比较大,随着高度的增加,逐渐离开了运动和舰首涡的影响区,使得垂向速度的波动也逐渐减弱。整体而言,各位置处垂向速度的标准差随着高度的增加有减小的趋势,在离甲板比较近的区域中,垂向速度的标准差相对比较大,随时间的波动比较强。各位置在不同高度处的垂向速度标准差都小于1.75 m/s,舰载机的起降环境相对比较安全。
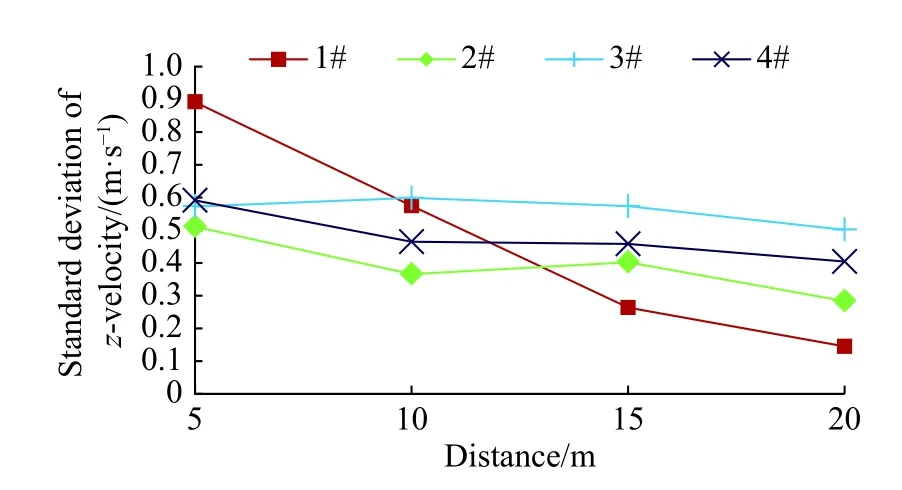
图12 不同高度处的垂向速度标准差Fig. 12 Standard deviation of vertical velocity at different heights
3.2 纵摇周期突变对流场的影响
在舰船航行的过程中,由于海浪和海风的不确定性,会带来舰船摇摆参数发生突变,特别是摇摆周期和摇摆角,使得舰面流场的变化难以预测。本节首先研究纵摇周期突变对舰面流场带来的影响。因此,在第120 s时将运动周期减半为10 s,此时最大纵摇角度依然是1.82°。变化后的舰船纵摇角速度为:

为了观察各个位置处的流场在纵摇周期突变前后的变化情况,图13给出了周期突变前后,第t=T个时刻甲板上方的流线对比图。该流线所在的纵向平面经过甲板上方10 m高度的4个观测点(黑点表示),同时流线用垂向速度着色。其中A图表示周期突变前的流场图,B图表示周期减半后的流场图。通过对比可以发现,当周期减半后,1#位置从之前的弱上洗流陷入了强下洗流,2#位置附近也出现了下洗流区域,会影响直升机的起降作业。3#位置前方出现了较强的上洗流区域,旋翼如果位于2#和3#位置之间,会受到向前的俯仰力矩,容易造成旋翼前倾。4#位置的前方也出现了较大的上洗流区域,后方有弱下洗流区域,旋翼如果位于4#位置,容易造成旋翼后倾。因此纵摇周期减半后,舰船摇摆速度加快,恶化了甲板上方的流场。

图13 周期突变前后的流场对比图Fig. 13 Comparison of flow fields before and after a sudden change in the pitching period
图14中给出了周期突变后,甲板上方10 m高度处观测点的垂向速度变化曲线。可以发现,大约在变化后的一个周期中,即120 s至130 s,由于受到运动变化的扰动,流场进入不稳定状态,在130 s之后,即周期突变后的第二个周期开始,1#位置处的流场重新稳定,其垂向速度又开始呈周期性变化,2#和3#位置的垂向速度在突变后的第三个周期开始出现周期性变化,4#位置的垂向速度大约在突变后的第五个周期开始才呈现出周期性变化,这与图10的结果相一致。相比于周期突变前的稳定状态,此时1#位置处的垂向速度变化范围有明显的增大,是因为1#位置离纵摇中心最远,当周期缩短后,舰船摇摆的频率加快,纵摇角速度增加,造成了甲板上方垂向气流的加速,对1#位置处的流场影响最大,同时舰首涡在1#位置附近刚开始形成,对其垂向速度影响较小,可以认为1#位置垂向速度的变化主要由舰船的纵摇运动引起,所以1#位置处的垂向速度变化范围明显增大。
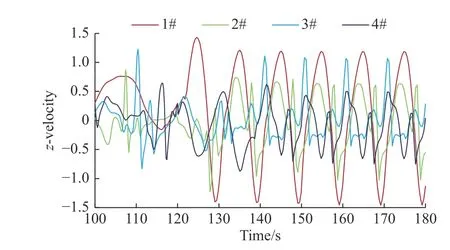
图14 甲板上方观测点的无量纲垂向速度变化曲线图(周期突变)Fig. 14 Variation of dimensionless vertical velocity at observation positions over the deck(with a sudden change in period)
图15中第0个周期段表示纵摇周期未突变的稳定阶段。当周期突然减小后,1#位置垂向速度的波动有明显的增大,随后有微弱的减小,从第二个周期后基本保持不变。比较特殊的是,3#位置在周期突变后,垂向速度的波动一直减小,直到突变后的第三个周期才有所增加,之后保持不变。还可以发现1#位置的垂向速度标准差最大,接近于CAP 437标准中规定的1.75 m/s,因此舰载机在该位置上进行甲板作业可能会引起安全事故。在纵摇周期突然减小后的稳定阶段,各位置垂向速度的标准差均大于突变前的。
图16给出了纵摇周期减小后,不同高度处的垂向速度标准差。可以明显观察到,1#位置的垂向速度在距甲板表面5 m高的地方出现了比较大的标准差,达到了2.88 m/s,根据CAP 437标准,如果舰载直升机在1#位置进行起降时,可能会由于垂向速度的严重波动而导致发生安全事故。对于其他三个位置,不同高度处的垂向速度标准差都小于1.75 m/s,且不同高度处标准差的变化并不明显,但总体上有随着高度的增加而减小的趋势。

图15 不同周期段的垂向速度标准差(周期突变)Fig. 15 Standard deviation of vertical velocity at different periods (with a sudden change in period)

图16 不同高度处的垂向速度标准差(周期突变)Fig. 16 Standard deviation of vertical velocity at different heights (with a sudden change in period)
3.3 纵摇振幅突变对流场的影响
在本节中,研究纵摇振幅突变后,对舰面流场带来的影响,在第120 s时将最大纵摇角度减半为0.91°,纵摇周期依然是20 s,变化后的舰船纵摇角速度为:
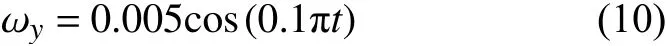
图17给出了振幅突变前后,第T个时刻甲板上方的流线对比图。其中A图表示振幅突变前的流场图,B图表示振幅减半后的流场图。通过对比可以发现,当振幅减半后,1#位置后方的下洗流区域减小,2#和3#位置周围的流场没有明显的变化,4#位置周围的上洗区域消失,总体来说纵摇振幅减半后,舰船摇摆变得平缓,改善了甲板上方的流场。
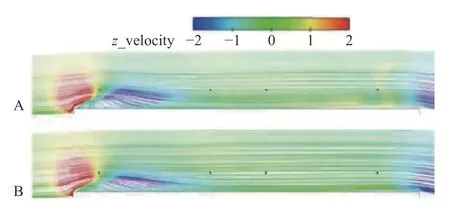
图17 振幅突变前后的流场对比图Fig. 17 Comparison of flow fields before and after a sudden change in the pitching amplitude
图18给出了振幅突变后,甲板上方10 m高度处观测点的垂向速度变化曲线图,从中可以发现大约在变化后的第一个周期中,即120 s至140 s,由于受到运动变化的扰动,流场进入不稳定状态,但在140 s之后,1#位置的流场重新稳定,其垂向速度开始呈周期性变化,其他三个位置处垂向速度周期性也基本建立,但有微小的波动。相比于变化前的稳定状态,此时各位置垂向速度变化明显减小,这是由于舰船纵摇角速度的减小而引起的。值得注意的是,1#位置的垂向速度都为正数,表示该位置完全处于上洗流中,而变化前该位置处于上洗流和下洗流的交替变化中。
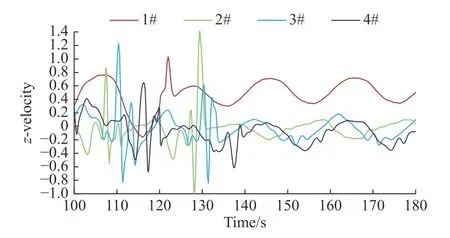
图18 甲板上方观测点的无量纲垂向速度变化曲线图(振幅突变)Fig. 18 Variation of dimensionless vertical velocity at observation positions over the deck (with a sudden change in amplitude)
在图19中,第0个周期段表示纵摇振幅未突变的稳定阶段,当振幅突然减小后,纵摇程度变得比较轻缓,1#、3#和4#位置处垂向速度的标准差都有所减小,而2#位置的垂向速度标准差在突变后先增加后减小,这一位置需要引起舰载机飞行员的注意。在第二个周期和第三个周期中,各位置垂向速度标准差基本一样,得到了和图18中一致的结果,即各位置处流场的变化从第二个周期开始就可以基本建立起周期性。还可以发现在纵摇振幅突然减小后的稳定阶段,各位置垂向速度的标准差均小于突变前的。
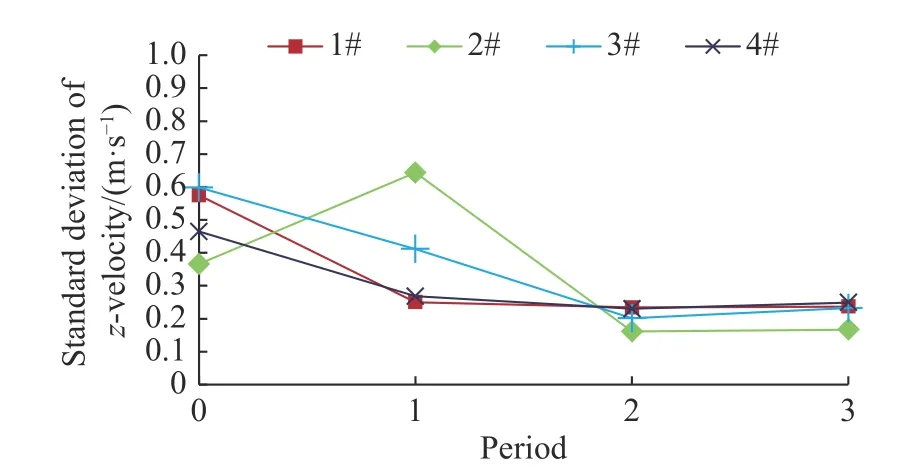
图19 不同周期段的垂向速度标准差(振幅突变)Fig. 19 Standard deviation of vertical velocity at different periods (with a sudden change in amplitude)
从图20中可以发现,当纵摇振幅减小后,各位置处的垂向速度标准差比变化之前有明显的减小,最大只有0.59 m/s,位于1#位置的5 m高度处。而且,各位置上方流场的垂向速度标准差都随高度的增加而减小,其中1#位置在近甲板区域有比较大的垂向速度标准差。
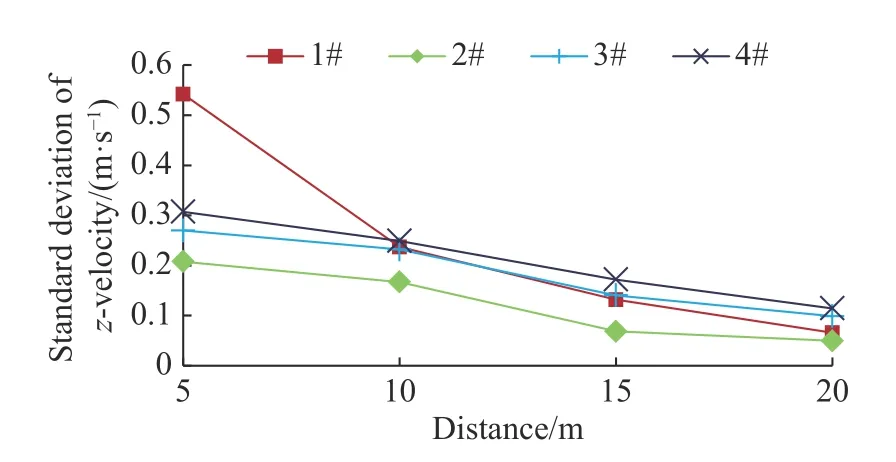
图20 不同高度处的垂向速度标准差(振幅突变)Fig. 20 Standard deviation of vertical velocity at different heights (with a sudden change in amplitude)
4 结 论
相比于以往关于舰船静止状态下的舰面流场研究,摇摆状态下的舰面流场更具有真实性,因此本文对舰船纵摇状态下甲板上方的非定常流场进行了数值模拟计算,并对流场中的涡结构和垂向速度变化情况作出分析和讨论,探究了舰船摇摆突变性对舰面流场的影响,得到的结论如下:
1)在顶风来流下,舰船在纵摇过程中主要产生舰首涡、边缘分离涡、上层建筑尾涡和舰尾涡,其中舰首涡和上层建筑尾涡会随着舰船的纵摇向后脱出一系列涡圈,导致流动变得非常紊乱复杂。
2)当舰船突然开始纵摇或纵摇周期突然减半后(其他物理量保持不变),甲板上方不同位置流场的周期性不是同步建立的,上层建筑和舰尾附近位置要分别滞后于舰首位置大约一个周期和三个周期才能建立起周期性流动,对于舰载机的起降作业需要认识到这种突变情况下的时滞性。周期减半后,舰船摇摆速度加快,恶化了甲板上方的流场,各位置垂向速度的标准差均有所增加,且在1#位置有明显的增加,其垂向速度的波动最大。
3)当纵摇振幅突然减半后(其他物理量保持不变),舰船摇摆比较轻缓,改善了甲板上方的流场,各位置垂向速度标准差在突变后都有明显地减小,除2#位置垂向速度标准差在突变后先增加后减小。同时振幅突变对1#位置带来的上下洗流变化也会影响舰载直升机的安全起降。
4)在不同情况下,各位置处的垂向速度标准差都随着高度的增加有减小的趋势,在离甲板比较近的区域中,1#位置垂向速度的波动明显强于其他位置,因此舰载直升机的起降作业应该远离该区域。
基于真实海况,舰船会出现不同方向上的摇摆和振荡之间的耦合运动,同时受到横风的影响,使得舰面流场将会更加复杂多变,难以预测。本文只进行了正向来流下,舰船模型在做简谐运动时的简单研究,对纵摇状态下的流场得到了初步的认识。后期将引入不同风向角以及舰船的耦合运动,对舰面流场展开更深入的研究,以期为舰载直升机的安全起降提供更加全面、合理的建议。

