常见最值问题的解题策略探究

■石狮市实验中学 赵 平

最值问题的有效解决，一直是学生学习过程中的重点和难点。如何有效突破，进而提升学生的综合解题能力，是一线数学教师一直反复思考的问题。笔者认为，有效解决最值问题的有效策略是：识别模型、解法归类、分解化归、熟练应用。以下笔者结合查阅的资料和课堂的教学实践，对常见的最值问题及解题策略进行梳理和归纳。

一、最值问题的常见解题策略

几何类最值问题的基本解题策略是：将相关数学问题（如果是实际问题，应先抽象为数学问题）转化为可以利用“两点之间，线段最短”“垂线段最短”“三角形两边和大于第三边”等几何定理解决的问题，并加以解决。其中“两点间线段最短”是解决几何最值问题中最本质、最核心的依据，因而也是我们进行问题转化的出发点和落脚点。在解题中应给予十足关注，才能方向明确，游刃有余。代数类最值问题的基本解题策略是：选择适当的变量，并建立该变量与目标变量之间的函数关系（含对应关系、自变量的取值范围），并利用函数的图像、性质（增减性）等相关知识解决问题。其中函数的连续性是前提，增减性是保证，而在本质上是求函数值的范围，因此体现函数三要素的有机统一。代数类最值问题也常常可以通过配方法将代数式转化为完全平方式，并利用完全平方式的非负数加以解决；有时也可利用根的判别式建立不等式模型并加以解决。

二、常见最值问题的实例与赏析

（一）代数类最值问题及赏析

【例1】已知反比例函数y=，其中k＞-2，且k≠0，1≤x≤2。若该函数的最大值与最小值的差是1，求k的值。

【赏析】本题以反比例为载体求最值问题，是很典型的代数类最值问题，基本思路为通过函数增减性及自变量取值范围求解，因为在自变量的不同取值范围内其最值往往是不同的，所以经常需要关注分类讨论，这是代数类最值问题解题的基本方法之一。如果在解题过程中能结合函数图像进行辅助性解题，则能更好地体现函数在求最值中的作用。

【例2】（2017年福建中考改编）已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M（1，0），且a＜b。若直线与抛物线的另一个交点记为N。（1）若-1≤a≤，求线段MN长度的取值范围。（2）求△QMN面积的最小值。

【赏析】本题是典型的应用函数或方程或配方求最值的代数类最值问题题目，全面体现了代数类最值问题的基本解法。（1）求MN范围，即为求MN最值。解题的关键是在画好图形的基础上（如图1），求出MN的表达式（用含a的代数式表示），并通过配方法或函数的性质加以解决。（2）解题的关键是在画好图形的基础上（如图1），求出△QMN的面积S的表达式（用含a的代数式表示），并通过配方法或函数的性质或根的判别式加以解决。

（二）几何类最值问题及其赏析

【例3】如图2，长方形ABCD中，AB=6，BC=4，在长方形的内部以CD边为斜边任意作Rt△CDE，连接AE，则线段AE长的最小值是______。

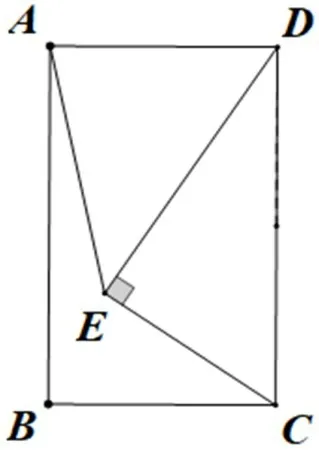
图2

图3

【赏析】本题的解题的关键在于找到动点运动的路径（轨迹）（如图3），再利用“两点之间，线段最短”即可求出最小值。

【赏析】

（1）依题意画图，为结合最值的解决提供载体，这是解决几何最值问题的起点。（2）本题俗称“阿氏圆”问题（如图4），解题的关键是利用“三角形相似对应边成比例”将。TB转化为一条线段，并利用“三角形的两边之和大于第三边”解决，体现了几何类最值问题的解题本质，其中抛物线仅为载体而已。

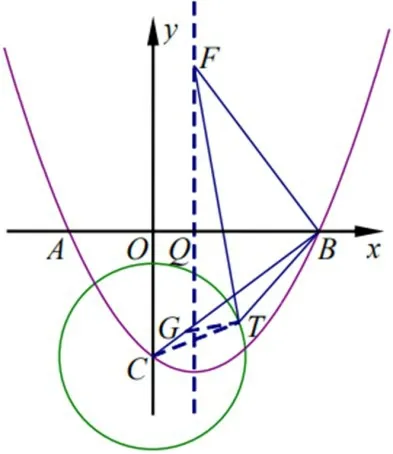
图4

【例5】如图5，四边形ABCD是菱形，AB=6，且∠ABC=60°，M是菱形内任一点，连接AM，BM，CM，则AM+BM+CM的最小值为________。

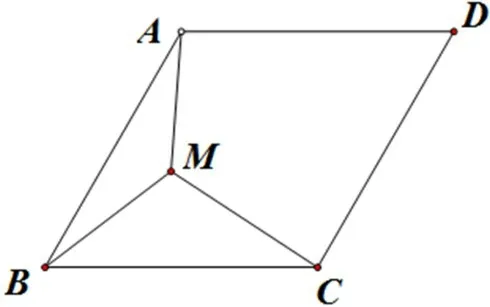
图5

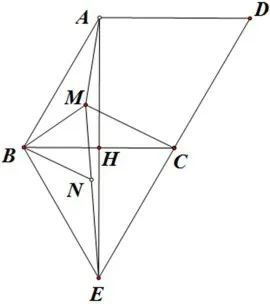
图6

【赏析】本题俗称“费马点”问题，解题的关键是通过旋转60°构造等边三角形，将三条线段（AM，BM，CM）转化在同一条直线（AE）上（如图6），再利用“两点之间，线段最短”解决问题，很好地体现了几何类最值的解题本质。

总之，识别模型、解法归类、分解化归、熟练应用，是有效解决最值问题的有效策略，在数学的学习与研究中教师应给予关注和强化，以更有效地提升数学学习效益。