阻滞增长演化网络的拓扑性质
彭 莎,覃 森
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
当前,众多现实社会系统,如社会网络中的谣言传播、电路交通网络等均可抽象为复杂网络,即将具体的对象和对象之间的关系抽象为网络中的节点与边[1-2]。复杂网络复杂性的重要体现之一是网络演化规则的复杂性。1999年,Barabàsi和Albert[3]提出了无标度网络(Scale-free Network, SF),利用节点增长性和新边择优连接性来解释现实社会中普通存在的“富者更富”现象,引起许多领域科学家的广泛关注。后续的研究表明:SF网络中增长模式与某些现实社会的节点与边增长方式并不吻合,如社交网络中同一时间会有多个新用户加入网络[4]、网络每次增加边数可能存在非线性增长或加速增长的特性[5]。此外,网络增长中存在节点的加入与衰退现象,例如:生态网络中,当生命结束时节点也会随之消失[6],而且每个节点对于环境的适应能力也不同[7]。另一方面,网络的新边连接方式不仅有择优连接,还存在随机连接和反择优连接等[8-9]。深入研究网络的演化特点获得特殊的演化规律,对于网络拓扑特性分析、动力学行为探索和网络控制均具有重要的理论意义和实用价值。在SF网络的基础上,本文提出Logistic阻滞增长网络模型,每一步添加到网络中的边数不是恒定的常数,而是符合Logistic增长,得到单个节点的度演化规律。
1 Logistic阻滞增长
人口预测问题中的指数增长模型是一类简单的生物增长模型,其最大的不合理之处在于没有考虑环境的制约。而Logistic阻滞增长考虑自然资源和环境条件等因素,能有效预测人口增长的规律,在生产预测等方面应用广泛[10]。SF网络的演化规则中,每一步添加到网络中的边数是常数m,本文在网络新增边数的规则中引入Logistic阻滞增长模式,即每一个演化时间步t,一个新节点附带到网络中的新边数m(t)满足如下规则:
(1)
式中,a是演化网络中第一步的新增边数,r是每一步连接网络中新边的增长速率,L是网络最大容纳量,即每一步添加到网络中的最大边数。众多社会系统可抽象为复杂网络,网络演化过程中,每添加一个新节点,新节点与网络中已有的m(t)个节点进行连接。在初始阶段的网络中,节点数量少,添加到网络中边数少,但增长速率快;增长一段时间后,网络中节点和边数增多,此时增长速率减缓但是仍然处于增长阶段;由于不能无限增长,最后达到网络最大容纳量,此时网络中节点多,基数大,以最大值保持不变。因此,每一步添加到网络中的边数呈现Logistic阻滞增长。L和r分别为Logistic增长每一步添加到网络中的最大边数和增长速率,a为第一步添加到网络中的边数,本文的研究针对L和r,研究其对网络拓扑性质的影响,不考虑a对Logistic网络的影响,故a取一个较小常数4。
每一步添加到网络中的边数m(t)随着时间增长的变化情况如图1所示。图1(a)中,当r=0.002时,L的取值分别为5,10,15和20。可以看出,L取定一个数值,随着t增大,每一步的网络新增边数m(t)增加并将稳定于网络的最大容纳量L。例如L=20,m(t)会增加到20,则后续每一步的网络新增边数m(t)恒为20。图1(b)中,当L=20时,r的取值分别为0.001,0.002,0.005和0.010,可以看出,增长速率r越大时,新增边数m(t)越快地达到最大值。

图1 网络新增边数m(t)随时间t变化曲线
2 具有Logistic阻滞增长特性的演化网络
2.1 网络模型构建
SF网络中,每一个时间步增加一个节点且带有m条新边,以择优连接方式进行连边。本文构建具有Logistic阻滞增长特性的演化网络,即每一步新节点附带着的边数满足Logistic阻滞增长曲线。具体演化步骤如下。
(1)Logistic增长。初始网络为由m0个节点组成的连通网络,每一步增加一个新节点,该节点与网络中的m(t)个节点连接,m(t)满足式(1),且m(t)≤t+m0。
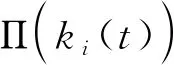
ki(t)表示在t时刻第i个节点的度。随着时间t的增加,网络规模不断增长,在时刻t网络的节点数为m0+t。当t足够大时,网络中的初始节点数可以忽略不计,即m0+t≈t。本文将时间t等价为网络规模的大小n。
2.2 节点度的性质分析
由于初始网络中有m0个节点,每一步增加一个节点且连接m(t)条新边。当时间t充分大且忽略初始网络边数时,网络中边的总数为:
新节点加入到网络中并与网络中已存在的第i个节点连接的概率为:
根据平均场理论,单个节点的演化方程如下:
假设节点i是ti时刻加入到网络中,则上述微分方程的初始条件为:
从而,解此微分方程得到网络中任意节点i的演化方程:
令r趋于0,可以得到:
(2)

图2 网络中,3个不同节点的度随时间t的演化规律

2.3 拓扑特性分析
2.3.1 度分布
由于Logistic阻滞增长模型的节点度演化方程为非线性的,其度分布难以获得解析结果,本文采用数值模拟的方法进行分析。从节点度的演化方程可知,SF网络是Logistic阻滞增长模型的一个特例。因此,这两类网络模型的度分布也呈现出相关性。不同的L和r情况下,Logistic阻滞增长网络的度分布情况如图3所示。
SF网络的度分布服从幂律分布P(k)~k-γ,在双对数坐标系中是斜率为-γ的直线[3]。探索L和r对Logistic阻滞增长模型度分布的影响,在数值模拟实验中,取n=20 000。从图3可以看出,Logistic阻滞增长模型的度分布在双对数坐标系中由两段斜率不同的直线组成,呈现出双幂律分布。在图3(a)中,前半部分线性拟合,直线斜率均接近于-3。这表明当网络增长边数L达到最大值,后续每一步添加到网络中的边数恒为最大值,网络演化退化为SF网络。后半部分度分布的线性拟合发现:斜率数值相差较大,且L越大,后半部分度分布下降越快,此时受Logistic阻滞增长的影响明显,从而与SF网络的度分布差别变大。
如图3(b)所示,在不同的r下,前半部分的度分布仍然符合SF网络,后半部分的度分布通过线性拟合得到直线斜率接近,并且r越小,双幂律分布转折点出现的越早。所以Logistic阻滞增长模型中的参数L和r分别决定了其双幂律分布后半部分的度分布指数与临界点的位置。

图3 网络在不同的L与r条件下的度分布图
2.3.2 平均路径长度
当复杂网络具有较小的平均路径长度和较大的聚类系数时,称它具有小世界特性。图4显示网络平均路径长度d在不同的L和r条件下随网络规模增长的变化情况。当网络规模固定时,L或r越大,网络的平均路径长度越小,这表明每步添加到网络中的边数越多可缩短节点之间的路径长度。如图4(b),固定L,随着网络规模增加,不同的r所对应的平均路径长度差距缩小,比如当n=7 000时,平均路径长度最大差距约为0.1。
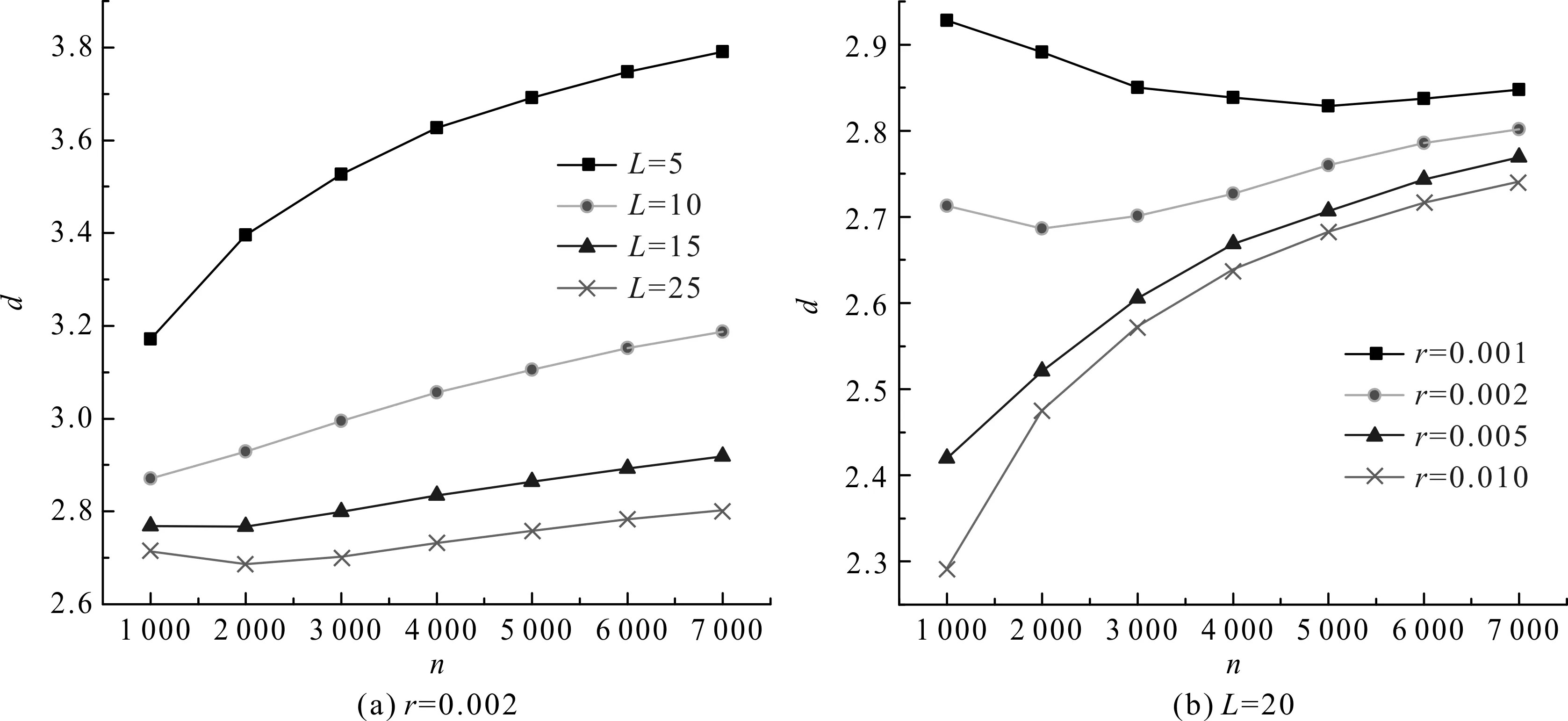
图4 网络在不同的L与r条件下的平均最短路径长度
2.3.3 聚类系数
当网络充分大时,SF网络不具有明显的聚类特征,其聚类系数C满足C~(lnt)2/t[11]。图5是Logistic阻滞增长网络的聚类系数C在不同的L和r随着网络规模的变化情况,Logistic阻滞增长网络的聚类系数较小,聚类特征不明显。其中图(a)和图(b)的内插图显示了在双对数坐标下,C在不同的L和r随着网络规模的变化情况。聚类系数随着网络的规模幂律递减,并且在双对数坐标中下降速度大致相同,即每一条代表不同参数的直线斜率接近相等,说明聚类系数随网络规模的变化速率与不同的L和r没有明显关系。
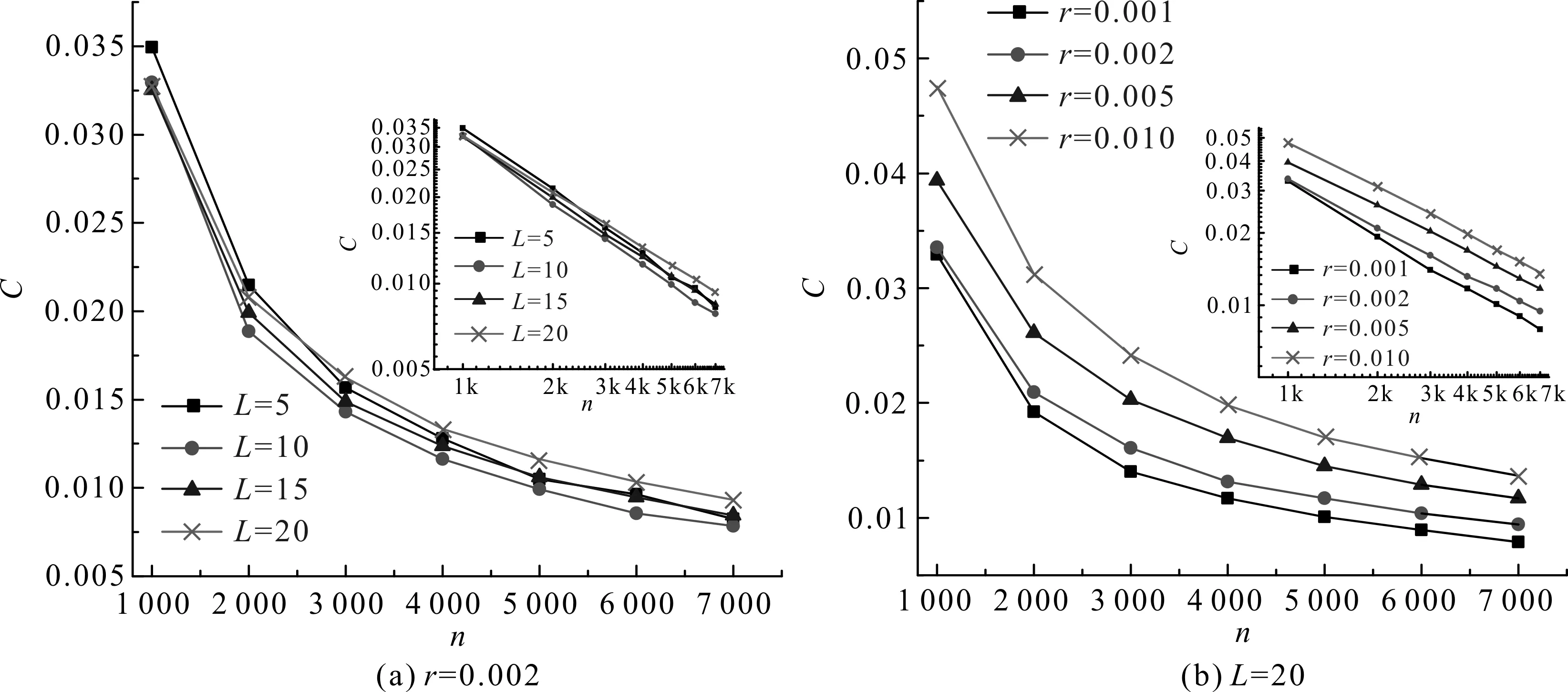
图5 网络在不同的L与r条件下的聚类系数
2.3.4 同配系数
同配系数s∈[-1,1]的大小反映了网络同配或异配的强弱程度。当s>0,网络是同配的,意味着网络中度大的节点倾向于与度大的节点连接;反之,称网络是异配的。图6显示了不同的L和r对网络同配系数的影响。数值模拟结果得到网络的聚类系数均是负数,表明网络是异配网络,这和添加到网络中的节点满足优先连接的性质相符合。图6(a)中,L越大对应的同配系数|s|越小,网络的异配性变弱。图6(b)中,网络规模n>5 000时,不同的增长速率r对应的网络同配系数接近相等。另外,随着网络规模增加,网络的同配系数趋于稳定。
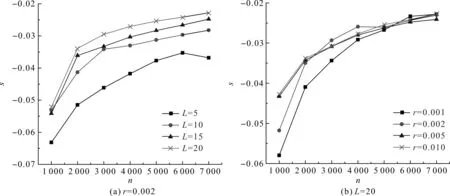
图6 网络在不同的L与r条件下的同配系数
3 结束语
基于SF网络的节点增长性,本文构建了Logistic阻滞增长网络模型,研究网络最大容纳量和增长速率的拓扑性质规律。数值模拟结果表明,网络是具有双幂律分布特性的异配网络。随着网络规模的增加,增长速率对网络的平均路径长度和同配系数的影响减弱,然而对聚类系数的变化趋势没有明显影响。网络的拓扑性质为进一步探索网络演化对网络拓扑性质的影响及其原因提供了方向,同时利用Logistic模型可有效地调节演化网络的度分布、平均路径长度、聚类系数和同配系数等拓扑特性,为研究Logistic阻滞增长网络的动力学行为和控制方法提供理论依据。

