基于认知无线电的GEO与LEO卫星频谱共存

胡晓月，杨淼，康凯,3,*，张舜卿

1. 上海大学 通信与信息工程学院，上海 200444

2. 中国科学院 上海高等研究院，上海 201210

3. 中国科学院 上海微系统与信息技术研究所 无线传感网与通信重点实验室，上海 200050

卫星通信具有覆盖面积大、地面干扰小等优点，被广泛关注[1-2]。其中低轨道(low Earth orbit, LEO)/中轨道(medium Earth orbit, MEO)卫星具有更小的传播时延和更低的传输损耗，使其可以在多个频带中被快速的部署,开创了商业通信应用的新时代[3-5]，这些包含数千颗,甚至上万颗小卫星的非对地静止(non-geostationary Earth orbit, NGEO)卫星可以提供高容量和低延迟的多媒体服务。

随着新的宽带多媒体应用的推出，对宽带无线频谱的需求大幅度增加，而由于当前的频谱分段和静态频谱分配策略，使得可用的频谱资源变的越来越稀缺[6]。但是在对已分配频段的频谱利用率进行大量的测量后，发现平均的频谱利用率非常低[7]。为了提高频谱效率，需要探索有效的频谱共存技术，使不同的卫星通信系统共享同一个频段。

然而，随着大量的NGEO卫星投入运营，众多NGEO卫星与静止轨道(geostationary Earth orbit, GEO)卫星共享频谱资源，将会对GEO卫星造成严重的干扰，导致GEO卫星的通信质量降低，甚至处于瘫痪状态(NGEO卫星运行到GEO卫星与GEO地面站视线之间)。在这种情况下，探索有效的技术来减轻GEO和NGEO卫星网络频谱共存时的在线干扰，就成为了一个高度相关且具有挑战性的问题[8]。

认知无线电通信(cognitive radio, CR)被认为是不同的卫星通信系统频谱共存和干扰避免问题的有效解决方案。但CR技术面临着诸多挑战，其中最大的挑战就是如何在特定的空间位置、特定频段内快速的检测已授权用户是否存在，并在授权用户出现的时刻迅速做出反应，以避免对授权用户的干扰[9]。频谱感知(spectrum sensing, SS)作为CR的基础步骤就致力于解决这个问题。

SS技术在地面通信环境中有较为成熟的研究，常见的SS技术包含匹配滤波器法、循环平稳特征检测法、协方差检测法以及能量检测法等[10]。其中匹配滤波器法虽然性能较好，但需要主要用户(primary user, PU)的先验信息；能量检测法计算复杂度低，但在低信噪比(signal and noise ratio, SNR)条件下检测误差较大；循环平稳特征检测法以及协方差检测法，相比于能量检测算法，可以在较低的SNR下保持相对较高的检测准确性，但计算复杂度高。在卫星通信场景中，由于信道环境较为复杂，存在各种大规模衰落与小规模衰落，导致卫星通信的SNR较低。目前应用在地面通信中的SS技术大多不能适应卫星通信。

CR技术在卫星通信的环境下受到很多的关注，文献[4,8,11]对GEO和NGEO系统之间的干扰进行分析，文献[4]针对上行和下行共存场景提出了自适应功率控制技术，以减轻在线干扰；文献[8]针对NGEO卫星对GEO地面站造成的串联干扰提出了一种认知功率控制算法，同时制定并解决了GEO卫星地面站与NGEO卫星地面站间距离最小化的优化问题；文献[11]根据卫星的运动将空间维度转换为时间维度，从而简化了干扰模型，在此基础上采用自适应功率控制算法，提高了频谱效率。文献[5]介绍了一种通过倾斜的LEO卫星相控阵天线的法线方向来减轻线内干扰的方法。文献[6,12]利用认知波束跳跃系统，考虑在不活动的主波束中存在多个辅助用户的情况，其中文献[12]提出了一种贪心算法，根据业务需求灵活的分配卫星的机载资源，以提高频谱效率。文献[13-14]利用SS技术对PU的状态进行判断，寻找时间或空间维度上的频谱空洞。文献[13]利用接收信号的极化状态，使用最优极化合并技术在卫星终端中执行SS，以复杂度为代价极大的提高了频谱效率；文献[14]在GEO为PU、两个NGEO卫星为次要用户(second user, SU)的场景下，在将信号与噪声分开的基础上，判断GEO的状态并计算GEO信号的功率，同时推导了用于判断GEO状态的阈值及功率的闭式表达式。尽管这些文献已经讨论了GEO和NGEO卫星的共存问题，但其大多数都着重关注于干扰分析及功率自适应方案，需要PU的先验知识。

本文将GEO卫星设置为PU，多波束LEO卫星设置为SU，在每个点波束范围内都采用计算简单且不需要PU先验知识的能量检测方案进行频谱感知，判断在点波束范围内是否含有正在通信的GEO地面站。为了解决能量检测方案在低SNR信道环境中性能较差的问题，本文提出了基于动态阈值的能量检测算法，针对不同的SNR实时调整判决的阈值，以更准确地判断GEO的状态信息。同时本文将能量检测算法与波束跳跃方案相结合，根据检测结果动态的调整多波束LEO卫星的波束方向，在保护GEO不受LEO卫星干扰的同时提高系统的频谱效率。

1 系统模型与问题描述

1.1 系统模型

本文提出了一种在Ka频段内GEO卫星与LEO卫星共存的场景，如图1所示，两个卫星覆盖相同的地理区域，且覆盖区域内同时包含多个GEO地面站和LEO地面站。在该场景中，GEO卫星为PU，LEO卫星作为SU部署在距离地球550 km的轨道上。每一个SU都装备一个固定的信号天线以及可操控的多波束天线。固定信号天线可覆盖一个直径约为1 000 km的圆形区域，代表SU的最大覆盖范围。可操控的多波束天线共计可产生Nb个点波束，每个点波束覆盖直径为150 km的圆形区域。但在一个时隙中，只有M个波束处于活动状态，为M个处于不同波束中的LEO卫星用户提供服务。

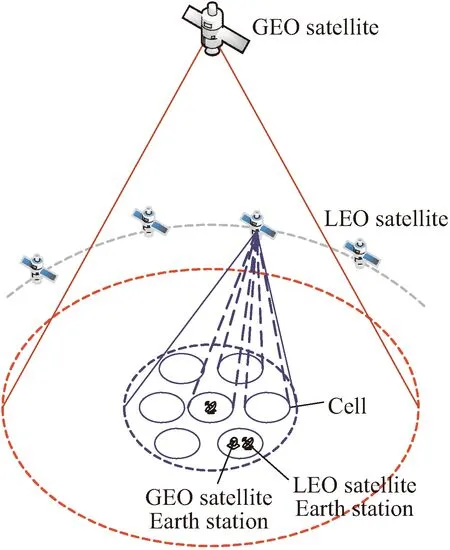
图1 GEO与LEO卫星频谱共存系统

在SU相对地球高速运动期间，SU首先利用固定的信号天线定期接收覆盖范围内所有LEO地面站的请求，然后根据接收到的Nu(Nu≥M)个请求，将处于激活状态的M个点波束随机分配给M个地面站。但由于SU地面覆盖范围与PU覆盖范围重叠，SU通信对处于同频段的PU通信产生了极大的干扰。为避免干扰，检测在每个点波束覆盖范围内是否存在GEO地面站正在与PU进行通信，若不存在，则该点波束覆盖范围内的LEO地面站与SU可成功建立通信链路；若存在正在通信的GEO地面站，则将波束随机分配给处于不同波束覆盖范围内的其他LEO地面站。

1.2 问题描述

根据提出的系统模型，本文考虑在上行链路中，应用SS技术来检测SU点波束覆盖的小区内是否存在正在与PU进行通信的GEO地面站。假设当GEO地面站正在与PU进行通信时，PU覆盖范围内的所有SU都可以接收到GEO地面站发送到PU的信息。为方便讨论，以SU的一个点波束为例，在每一个观察周期Tob内，SU通过接收信号判断GEO地面站是否存在。该问题可以定义为一个二元假设问题，当存在GEO地面站时，表示为H1，否则表示为H0[15]：

H0:y(n)=w(n)

H1:y(n)=hs(n)+w(n)

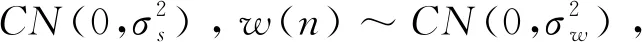
假设在一个观察周期中样本数量为N，则检测统计量可表示为：

Pd(γ)=P(Λ≥λ|H1)=

Pf=P(Λ≥λ|H0)=

其中Q(·)是标准的Q函数，Erfc (·)是余误差函数，为信道的SNR。为了提升检测的准确率，本文将会动态的选择能量检测的阈值λ，以提高检测概率Pd，降低虚假警报概率Pf。

2 基于SNR估计的动态阈值选择

2.1 信道SNR估计

在频谱感知的多种算法中，能量检测法是将收到的信号与预先设定的固定阈值进行对比，判断PU是否存在。由于其计算简单、硬件要求低以及不需要PU的先验信息等特点成为应用最广泛的算法。但其在检测的过程容易受到噪声的干扰，尤其在类似于卫星通信SNR较低的场景中，感知性能急剧下降。这种情况下，可以根据卫星通信的信道情况实时调整阈值，以提高检测的准确率。

在LEO卫星沿着固定的轨道高速运动时，如图2所示，其相对于特定的GEO地面站的距离d始终遵循着先变小再变大的规律。距离d具体表示为：

图2 LEO沿固定轨道高速运动系统示意

式中：Re为地球半径；Hs为卫星轨道高度；α为卫星与地面终端间的仰角。通过式(1)可以明显看出，当α=90°时，d达到最小值；当α=0°时，d达到最大值。

影响卫星通信信道质量的因素包括自由空间传播损耗、大气吸收损耗、降雨损耗、多径衰落等。自由空间传播损耗作为影响卫星通信的最主要因素，可表示为：

式中：Pt和Pr分别为发射功率和接收功率；Gt和Gr分别为发送端和接收端的天线增益；f为工作频率；c为电磁传播速度。根据式(2)可以得出结论，当工作频率f固定时，卫星通信的自由空间传播损耗主要由通信距离d决定。

若只考虑自由空间传播损耗，那么SNR可以计算为：

γ(dB)=Pt+Gt+Gr-Lf-kbBTe

式中：kb=-228.6 dBW/(K·Hz)为玻尔兹曼常数；Te为噪声温度；B为信道带宽。

2.2 动态阈值选择

如图3所示，LEO卫星过境期间SNR波动可以达到11.9 dB，若在此期间始终使用固定的阈值进行能量检测，则会极大增加检测错误率。为了提升检测性能，本文针对估计的SNR实时的选择能量检测的阈值λ。

图3 NGEO卫星过境期间SNR波动

在传统的能量检测算法中，一般根据虚警概率Pf选择阈值[16]：

但是当出现漏检情况时(当PU信号存在，检测结果为PU信号不存在)，SU若应用检测的频谱空洞进行通信，将会对PU产生极大的干扰。而本文致力于降低SU系统对PU系统的干扰，这种传统的阈值选择方法并不适用于GEO与LEO卫星通信系统共存的场景。本文在考虑Pf(λ)的基础上，同时引入了错误检测概率Pmd(λ)=1-Pd(λ)对阈值的影响，并以检测的总错误率Pe(λ)=Pf(λ)+Pmd(λ)表示检测的性能。可以将最优动态阈值归纳成如下的优化问题[17]：

最终的最优阈值可表示为：

根据估计的SNR动态选择最优的检测阈值，可以达到降低检测错误率的目的。

3 仿真分析

本节在应用Matlab软件在GEO卫星和LEO卫星共存的场景下，对基于动态阈值的能量检测算法进行了仿真。系统的仿真参数如表1所示[18]。

表1 仿真参数

针对不同的信道环境选择动态阈值的结果如图4所示，其中两条曲线分别代表在不同的SNR条件下，选择的归一化动态阈值λ以及一个观察周期内归一化的接收信号能量的变化趋势。可以明显看出，随着SNR的不断提高，LEO卫星接收信号的能量逐渐增大。为了使能量检测的错误率Pe最小化，选择的归一化动态阈值λ也随接收信号能量的增大而不断的上升。即当接收信号的SNR为-15 dB时，选择的阈值λ为0.76，SNR增加到5 dB时，动态阈值λ调整为1.20。

图4 不同SNR对应的归一化动态阈值与接收信号能量

在进行能量检测的过程中，根据选择的动态阈值对GEO地面站信号是否存在进行判别，其与应用固定阈值方法的检测性能对比如图5所示(仿真中固定阈值随机选择为0.79)。当采用传统的固定阈值法进行检测的过程中，可以明显观察到，当SNR在-13～-15 dB，检测的总错误率 在0.7～0.95波动。随着SNR的增加，总错误率Pe在不断下降，在SNR为-9 dB时达到最小值0.05，随后逐渐上升，最终在0.4附近波动。这种情况的出现是由于固定的阈值0.79在SNR为-9 dB时为最优阈值，但与其他SNR环境不匹配。应用传统的固定阈值检测法的整体性能表现印证了上文中所提到的观点，当信道环境较差时，传统的能量检测法性能急剧下降。而应用动态阈值进行能量检测时，可以明显看出，当SNR较低时，总错误率Pe在0.1～0.3波动，而随着SNR的逐渐增大，总错误率Pe趋近于零，其性能远远优于传统的固定阈值检测算法。

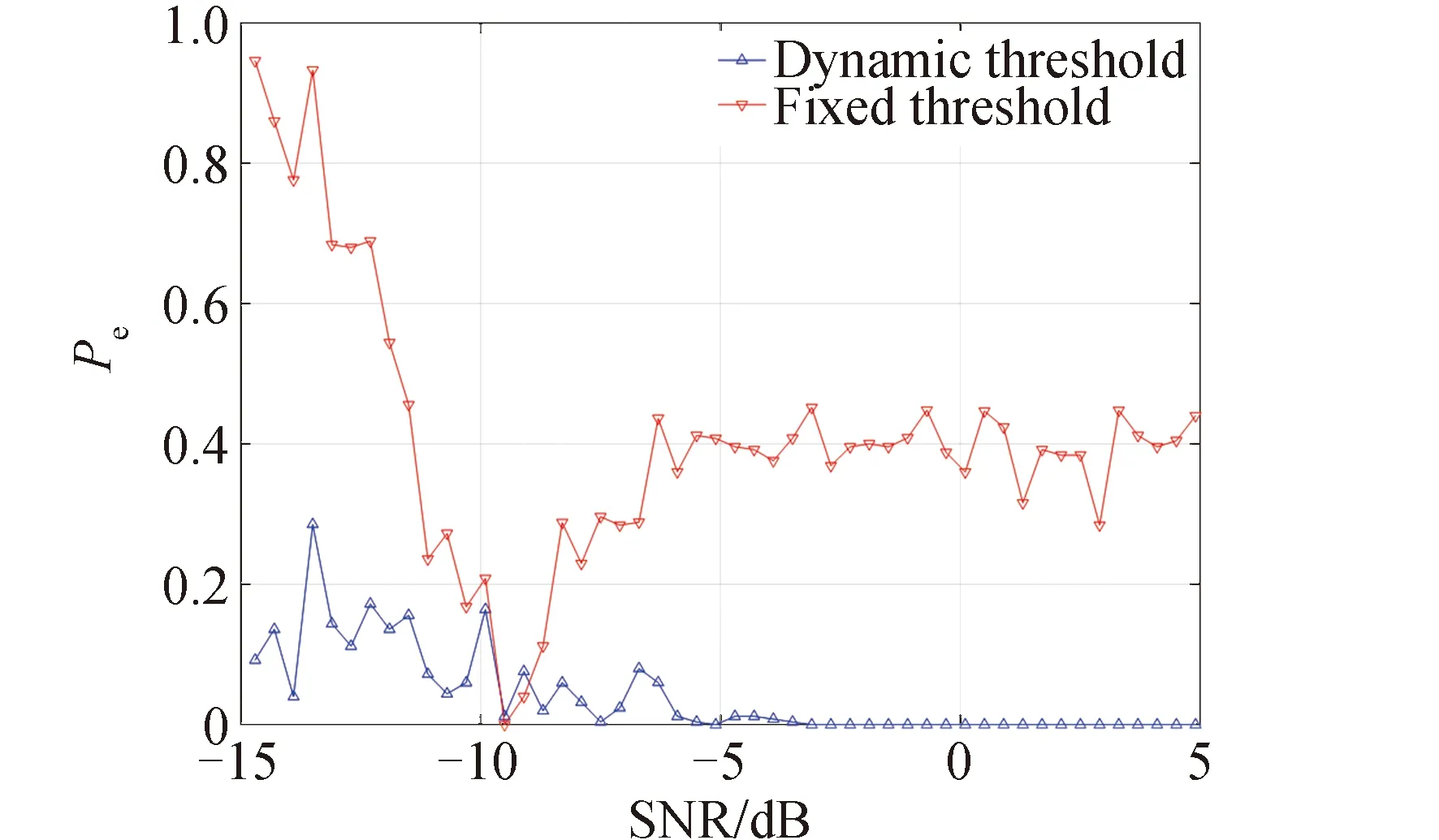
图5 基于动态阈值与固定阈值的检测性能对比(固定阈值为0.79)

前文中提到的循环平稳特征检测算法是利用接收信号的周期性特征来判断PU信号是否存在，有较好的抗干扰性。所以本文选择基于二阶循环统计量的特征检测算法[19]与基于动态阈值的能量检测算法进行对比，结果如图6所示。可以清晰地看出提出的基于动态阈值的算法性能要高于基于二阶循环统计量的特征检测算法，在SNR处于-15～5 dB，循环平稳特征检测算法的总错误率Pe始终维持在0.5左右。基于动态阈值的能量检测算法在SNR<-5 dB的情况下，总错误率最高为0.21；而在SNR>-5 dB的情况下，总错误率趋近于0。

图6 基于动态阈值的能量检测算法与循环平稳特征检测算法性能对比

4 结束语

本文针对GEO卫星与LEO卫星共存的场景，提出了基于动态阈值的能量检测算法，同时结合多波束LEO卫星的波束跳跃算法，提高了频谱利用率，降低了LEO卫星对GEO卫星通信的干扰。针对不同的信道环境采用最优的动态阈值进行能量检测，可以解决传统能量检测算法在低信噪比的环境下检测误差非常大的问题。在SNR较低时(SNR<-10 dB)，基于动态阈值的能量检测算法的平均误差比传统算法低87%；同时在SNR较高时(SNR>-5 dB)，前者的检测误差趋于0。与前人的基于二阶循环统计量的频谱感知算法相比，平均误差降低了88.4%。