部署retro-GEO巡视器的月球借力飞行轨道分析
贺波勇,马鹏斌,杜卫兵,李恒年
1. 西安卫星测控中心 宇航动力学国家重点实验室,西安 710043
2. 西北工业大学 航天学院,西安 710072
月球引力辅助甩摆力学原理最早可追溯至1687年牛顿的数学建模描述。Apollo任务中绕月自由返回轨道便是人类利用月球引力辅助甩摆提高航天员安全性的著名载人航天实践活动[1]。1990年,日本发射Hiten航天器,进行了双月旁转向飞行试验[2]。1998年,休斯公司利用月球甩摆实现亚洲三号卫星挽救转移轨道控制,成就人类第一次成功挽救人造卫星的航天传奇[3-4]。2000年,国内学者曾国强等[5-6]基于双二体圆锥曲线拼接模型研究了利用月球甩摆从地球高纬度地区发射地球静止轨道(geostationary Earth orbit, GEO)和逆行卫星轨道设计问题,表明利用月球借力发射逆行卫星可以节约一定能量,但采用简化动力学模型不能反映该类轨道参数属性。罗宗富[7]研究了双月旁转向轨道存在性力学机理与建模设计方法,一定角度上阐明了月球借力飞行的参数敏感性力学原理。彭祺擘[8]通过地月转移轨道一阶偏导数矩阵(状态传播矩阵条件数)分析了月球对轨道参数的快速非线性放大作用。随着GEO卫星数量指数增长,废弃卫星及碎片引起的GEO资产安全性问题日益严峻[9]。1984年,Oberg[10]开拓性地提出了retro-GEO(retrograde GEO)概念,并指出利用月球借力飞行部署该类轨道可以节约发射能耗。2001年,Kawase[11-12]提出利用retro-GEO监测GEO轨道带碎片构想。Aravind等[13]也通过简单的几何轨道模型比较了几种retro-GEO转移方案导致卫星剩余寿命的差别,但求解的retro-GEO轨道远低于GEO高度。可见,retro-GEO轨道可对GEO带全部资产每12 h巡视预警一次。但目前关于绕月飞行轨道设计方法模型精度不足,设计方法对参数敏感性高,且并未求解出符合要求的理想月球借力飞行轨道,也未对该类轨道参数属性进行分析。
1 问题背景
1.1 GEO资产安全性严峻
GEO轨道周期与地球自转周期相同,星下点覆盖区域稳定不变。许多导航、遥感、数据中继、气象、海洋监测和国土资源监测等重要卫星都部署在GEO轨道。由于GEO受摄动位置漂移的安全域限制和卫星数目指数性增长,几十年来,很多GEO重要位置都是多颗卫星共位控制而存在[14],加之火箭末级残骸、失效卫星及空间碎片等,GEO轨道相当拥挤。
2014年7月28日和2016年8月19日,美国分别以一箭双星方式成功发射GSSAP-1/2和GSSAP-3/4(geosynchronous space situational awareness program, GSSAP)4颗GEO轨道卫星,可通过升高或降低轨道高度对GEO资产进行邻域碎片预警,但轨道机动成本大大限制了巡视范围[15]。
1.2 西向发射条件不具备
如果直接西向发射部署retro-GEO,存在2个难题:
1)一般卫星均采用东向发射方式入轨,西向发射火箭一、二级残骸落点均不是常规无人落点区域,可能是人口密集、甚至境外区域,可能给人民生命和财产安全带来隐患,还可能引起外交纠纷和技术泄露风险。
2)东向发射可以利用成熟地面测控站行精确测控,而西向发射没有成熟测控站支持。
1.3 月球探测器技术成熟
月球是地球唯一的天然卫星,也是迄今为止人造探测器造访最多的天体。特别是2018年5月、12月中国分别发射的嫦娥4号中继星和探测器联合月球背面探测任务[16-17],经过数十个月昼月夜仍在工作,表明了中国通过嫦娥任务已成熟掌握月球探测器发射、精密轨道确定和绕月变轨等技术。
2 借力飞行轨道描述与建模设计
2.1 借力飞行轨道描述
retro-GEO相对于地球固连坐标系飞行周期约为12 h(也可略高或略低于GEO),每个周期可对GEO空间资产遍历巡视和邻域安全预警,如图 1 所示。

图 1 retro-GEO示意
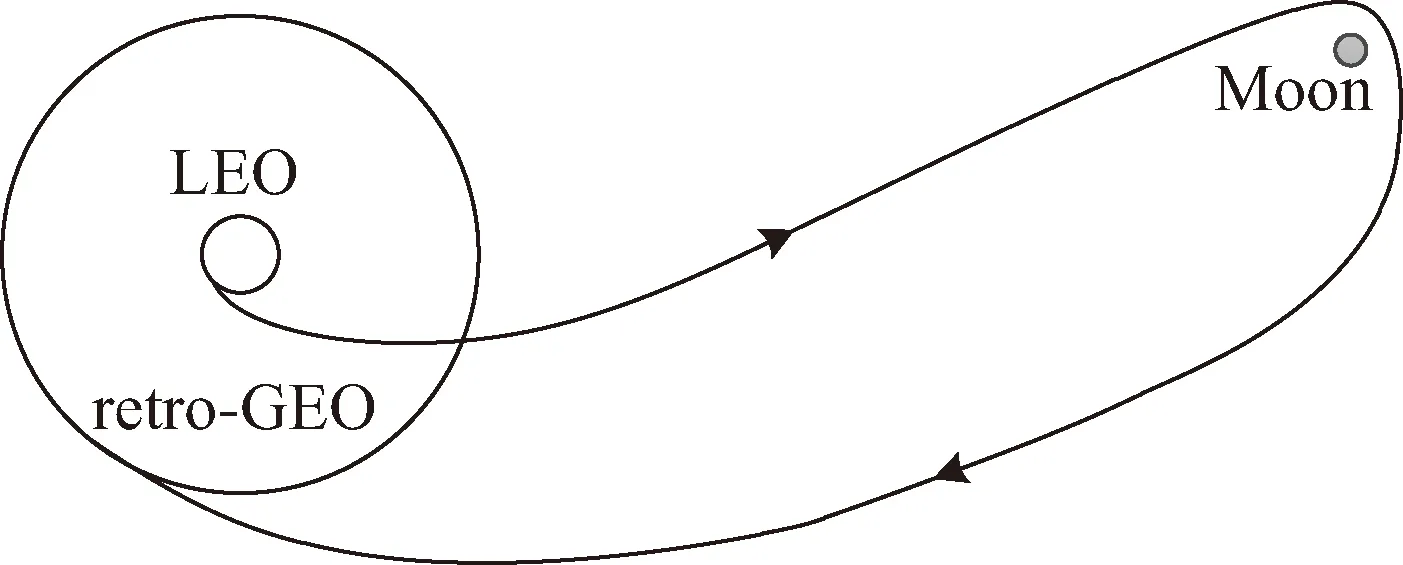
图 2 部署retro-GEO巡视器的月球借力飞行轨迹示意
如图 2 所示,利用月球借力飞行部署retro-GEO巡视器飞行轨迹是指从近地停泊轨道(low Earth orbit, LEO)切向施加一次脉冲,进入地月转移段,利用月球引力辅助甩摆后返回地球附近,近地距与GEO高度相同(可略高或略低),相对于地心J2000.0坐标系倾角为180°,在近地点施加一次切向脉冲减速制动形成retro-GEO巡视轨道。
(1)约束条件

(2)设计目标
从LEO出发至retro-GEO需要两次制动速度脉冲,设ΔvTLI和ΔvRGI(下标“RGI”表示retro-GEO insertion,逆行GEO捕获)分别为从LEO加速出发的速度增量和月球甩摆返回地球至GEO高度的减速制动速度增量。轨道设计时希望在满足约束情况下,轨道制动燃料消耗小,便于携带更大有效载荷,即
一、本刊设有专家论坛、述评、论著、学术交流、专题笔谈、综述、讲座、临床病理(例)讨论、教学园地、问题解答、临床研究、病例报告、误诊误治、技术改进等栏目,接受全国各地来稿。
Jmin=ΔvTLI+ΔvRGI
(1)
2.2 轨道设计建模
(1)轨道动力学模型
在绕月飞行轨迹参数初步设计分析时,通常会使用圆锥曲线拼接模型和圆型限制性三体模型(circular restricted 3 body problem, CR3BP)等简化轨道动力学模型。前者因其半解析特性,在Apollo任务分析中广泛运用,但在计算飞行时间较长的地月转移轨道设计问题中误差很大,甚至得到错误的结论[18-20]。而后者全时段同时考虑地月引力,结论可信度高,但需数值积分运算。
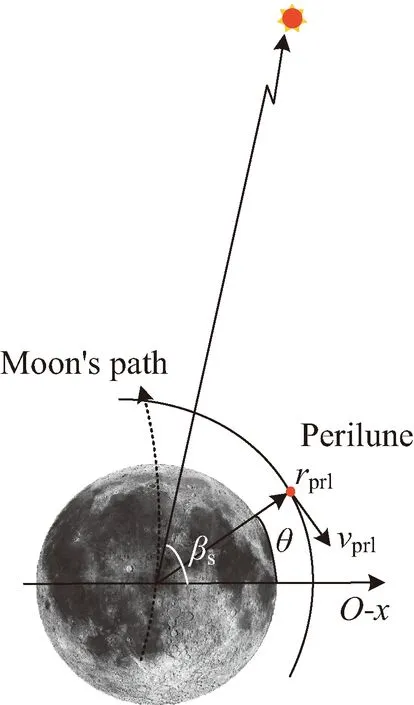
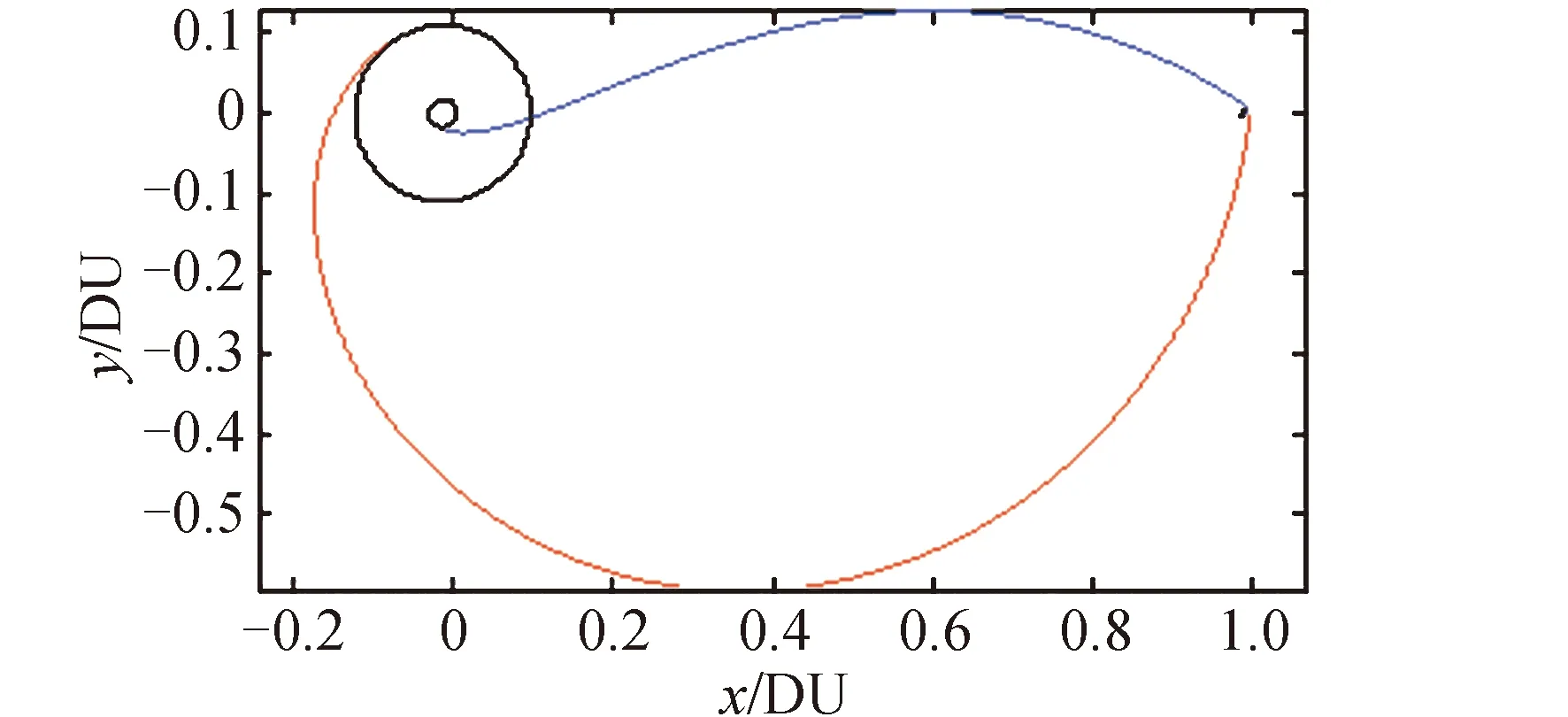
CR3BP是指存在两个主天体P1和P2,对应质量分别为m1和m2,相互绕其公共质心匀速圆周运动,研究质量为m≪m2 这里引入等效势能函数 表1 考虑太阳摄动地月空间引力场常数[21] 由于地月转移轨道在月球影响球附近受到的地球和月球中心引力均小于6×10-3m/s2,这时太阳中心引力摄动约为6×10-3m/s2[22],应在CR3BP基础上考虑第四体P3,对于地月系统而言,即考虑太阳摄动的双圆限制性四体模型(bi-circular restricted 4 body problem, BR4BP)更接近真实的地月空间引力环境。由于白道面与黄道面仅相差约5°,简化认为是日地月处于同平面。双圆是指地月围绕其公共质心做圆周运动和地月公共质心围绕太阳也做圆周运动的假设。第三体P在平面内的动力学方程为 等效势能函数 t时刻太阳相对于O-x轴的相位角为ωst,对应的位置为(ρcos(ωst),ρsin(ωst)。此时,第三体探测器P与太阳距离为: (2) 轨道设计模型 如文献[8]所述,月球借力飞行后,地月转移轨道状态传播矩阵条件数快速增大。对于部署Retro-GEO巡视器轨道而言,如果以TLI时刻飞行状态为设计变量,势必增加了轨道设计变量的敏感性和设计难度。本文提出以近月点时刻飞行状态为设计变量,分别瞄准匹配近地出发和绕月返回地球段约束条件,完成轨道设计。如图3所示,设近月点时刻太阳相对地月连线角为βs,月心距为rprl,近月点相对于地月连线角为θ,近月点速度大小为vprl,则可完全确定一条月球借力飞行空间轨迹。 图 3 近月点设计变量 以该时刻状态分别逆向和正向数值积分,可以同时计算地月转移飞行段和月球借力后返回地球段轨道参数。在实际计算时,并不知道一组近月点参数描述的月球借力飞行轨迹的近地出发时刻和绕月返回地球时刻。这时需要将逆向数值积分到近地出发时刻的飞行时长和正向数值积分到返回地球近地点时刻,分别参数化为Δtd和Δtr。由于文献[5,13]都没有成功求解严格满足近地出发和绕月返回Retro-GEO严格要求的转移轨道,本文设计轨道时,先不把式(1)所示的两次脉冲和最小作为优化目标函数,而需将惯性参考系中近地切向加速出发条件和出发时刻地心距、返回地球近地点时刻和返回时刻地心距都作为优化目标函数,则轨道设计转化为优化问题求解的模型为 式中,由于采用归一化的CR3BP和BR4BP模型,月球公转角速度为1,将近地出发和返回地球近地点约束统一未加权作为目标函数;rTLI、vTLI、rRGI和vRGI为惯性参考系中位置和速度矢量,而式(2)和式(4)中位置和速度均为会合坐标系中变量,相互转化关系如下: (3)轨道动力学模型延拓策略 为了求解式(7)轨道设计问题,先不考虑太阳摄动,利用较简单的CR3BP轨道动力学模型。即设计变量不考虑βs,并将Δtr设置为变量,利用MATLAB集成优化工具包中Multi-start求解(在优化变量区间内随机给出多个初值,以每个初值局部搜索),如图4所示。 图 4 延拓求解策略流程 再将CR3BP模型下的轨道设计变量当作设计变量初值,在某个Δtr固定值情况下,将βs在0~2π区间内遍历搜索,利用Matlab集成优化工具包中的fmincon求解,在结果中选出目标函数值最小的βs对应设计变量作为最优设计变量。两步延拓求解策略流程。 为了充分利用月球引力作用,设置归一化的近月距rprl∈[4.777,5.777]×10-3,参考文献[23],设置近月点速度vprl∈[2.3,2.7],近月点至近地出发逆向飞行时长Δtd∈[-0.8,-0.5],θ∈[-π,π]。计算得到CR3BP模型和BR4BP模型最优目标函数随Δtr∈[0.8,1.8]变化情况如图5所示。 图 5 最优目标函数变化 可见,只有当Δtr≈1.1 TU时存在最优解。当Δtr=1.1TU时,近月点时刻太阳处于方位对式(7)中目标函数影响如图6 所示。可知,太阳位于最优摄动方向(βs≈152°),才可以找到目标函数值最小的情况(式(7)中J≤7.0×10-5),此时月地段实际飞行时长约为114.79 h,该条轨道归一化后的平面轨迹如图7所示。 图 6 太阳不同方位摄动影响 图 7 部署retro-GEO巡视器的月球借力飞行轨迹 由图6可知,式(7)目标函数值处于较小值要求太阳位于的摄动方向分布范围有限,即日地月相对运动引起的发射窗口较小。说明该类轨道存在条件较为苛刻,也从另一个角度解释了文献[5,13]没有成功求解该类轨道的原因。 基于CR3BP和BR4BP模型,提出了利用近月点状态为设计变量的部署retro-GEO巡视器的月球借力飞行轨道求解方法,仿真算例表明: 1)以近月点状态为设计变量可有效减弱轨道状态传播矩阵的非线性快速增大效果,便于利用通用局部梯度优化工具求解,延拓策略可为复杂问题提供较为精确的设计变量初值,便于快速收敛; 2)部署retro-GEO的月球借力飞行轨道存在条件苛刻,只有近月点至返回地球近地点飞行时长约为114.79 h,且太阳处于最优摄动方向时,才可以找到理论意义上目标轨道。 本文揭示的该类轨道存在条件可为下一步求解该类轨道高精度轨道动力学模型解提供设计变量初值参考。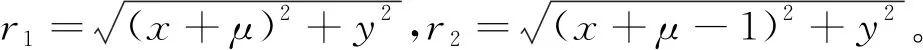


3 算例验证


4 结束语

