基于多维度控制的数控加工变形控制方法研究

吴艳芳，高鹏

(淄博市技师学院，山东 淄博 255000)

0 引言

随着科学技术的不断发展，机械制造业也随之不断进步。数控机床属于机械制造领域的核心设备。数控机床在加工过程中，其动态特性直接影响工件的形态以及生产效率。加工企业为了能够得到更多的利益，需要通过工件生产的较高效率实现。因此，数控机床加工效率的提高越来越得到重视。数控加工变形的研究受到相关学者的广泛关注，并对其进行深入研究[1-2]。

文献[3]提出将精确预拉伸技术引入到数控机床中，提高数控机床的精度稳定性。该方法优化丝杠传动结构，分析新的丝杠精确预拉伸方法，解决不能精确控制丝杠预拉伸量导致丝杠滚道变形的问题。该方法通过拉伸量控制，实现了数控机床加工工件时形变的控制，但该方法仅仅考虑了最大的丝杠传动结构，较为片面，控制的精度不佳。文献[4]提出基于扰动观测器的机床加工误差迭代学习控制方法。该方法分析了数控机床运行轨迹，创建了机床进给系统误差平面简图，建立驱动系统动力方程式，在经典比例微分(PD)控制方法的基础上，采用李雅普诺夫函数对改进后的控制方法进行证明。该方法采用PD控制方法，缩小了数控机床双轴加工时产生的误差，但该方法操作过程较为复杂，导致数控机床加工时间较长。基于上述问题的存在，本文提出基于多维度控制的数控加工变形控制方法。

1 基于多维度控制的数控加工变形控制方法

1.1 多维时间序列的数控机床加工变形参数采集

进行基于多维度控制的数控加工变形控制方法研究，需要对数控机床加工变形参数进行采集，采用自回归平均模型以及多维时间序列状态模型对数控机床加工变形参数进行采集。

1) 自回归移动平均模型

自回归移动平均模型是用于分析时间序列的核心技术。其针对非指定的数控加工数据时间序列Y={y1，y2，y3，…，yh}，在时刻h的取值为yh，其不但和前m个时间段的数控加工参数值yh-1、yh-2、yh-3、…、yh-m存在较大关联性，还和n个非指定白噪声干扰项bh-1、bh-2、…、bh-n也存在较大关联性，那么(m，n)阶的ARMA模型yh为

(1)

式中:bh代表误差干扰项；δ代表自回归系数；β1为移动平均系数；如果β1=0，那么自回归模型为AR(m)；如果δ1=0，那么移动平均模型为MA(n)。

考虑到数控机床加工参数真实属性，基于序列y构建自回归方程。

如果数控加工序为y={y1，y2，y3，…，ym，…，y2m}，

那么数控加工序列元素符合方程：

(2)

2) 多维时间序列状态模型和判断模型

多维时间序列可理解为检测数控加工变形参数的一组指标，在差异时段中得到一组检测结果，同时根据数控加工时间顺序排列而建立的数字集[5]。如果数控机床加工参数共有n种类型，同时按照固定采样频率得到m个数值点，那么将Hn×m设成数控机床加工过程数据的n行m列的多维时间序列矩阵。

按照对应分类标准，将数控加工参数设成非多维时间序列向量y1与多维时间序列矩阵y=[y1，y2，y3，…，yn]，伴随时间h的改变而发生变化。

在机床参数时间序列矩阵Hn×m中，设定数控机床加工的状况模型为采样时间跨度为M的序列矩阵几何，描述数控机床设备状况加工变动趋势。

将数控机床的历史状态设成时间窗口M中矩阵集合为H={H1，H2，H3，…，H(m/M)+1}，其中H(m/M)+1代表需采集的数控机床加工变形数据。

围绕数控机床加工状况模型矩阵Hn×m，构建一致加工状态衡量标准与评估函数。通过特征向量、特征趋势距离标识状况模型，使用差异性将数控加工状况实施进行判断[6]。

假设随机数控机床加工状况矩阵Ht∈Hn×m，变形特征向量Gt={gty，gtx}，依次描述数控机床加工变形状况矩阵内某时间段向量和平均值向量最高、最低偏差量为：

(3)

式中Hj为数控加工变形参数处于M时刻点hi的参数值。

针对随机数控机床加工状况矩阵Ht∈Hn×m，数控机床加工变形特征趋势间距设为二范数Et，判断获取数控机床加工变形的变动规律与平稳性特征矩阵Et(Hn×m) 为

(4)

二元组Ft=(Fj，Ei)由变形特征向量与变形特征趋势间距构成，那么随机两个变形状态Hj与Hi的差异水平εji为

(5)

数控机床加工状况的差异水平能够判断数控机床加工状况间整体差异，差异水平较大表示加工状态矩阵吻合水平较差，加工变形相似度较大，否则加工变形相似度较高，以此实现数据机床加工变形参数多维度采集。

1.2 基于多维度控制的误差补偿方法

基于多维度控制的误差补偿方法主要通过直线运动补偿方法、圆弧运动补偿方法完成多维度变形控制[7-9]。在获取的数控加工变形参数基础上，使用直线运动补偿，对其实现三维空间内随机直线方向补偿[10]，然后使用圆弧运动补偿，实现三维空间内圆弧方向补偿[11]，最终实现多纬度控制的误差补偿。

1)直线运动补偿

将获取的数控加工变形参数加工变形直线k的起点与终点坐标设为(P1，Q1，R1)、(P2，Q2，R2)，第j个插补点坐标设成(Pj，Qj，Rj)，直线k在PQ平面中的投影依次和P轴、Q轴夹角设为v、u，直线k和PQ平面内投影的夹角为o。

(6)

式中将插补点设为j，按照插补点坐标实现数控加工变形的直线运动补偿[12]。

2)圆弧运动补偿

将圆心角设为τ，起点、终点向量和P轴正向夹角依次设成τ1、τ2，圆弧起点、终点和圆心坐标依次设成(P1，P1)、(P2，Q2)、(P0，Q0)，第j个插补点坐标设成(Pj，Qj)。

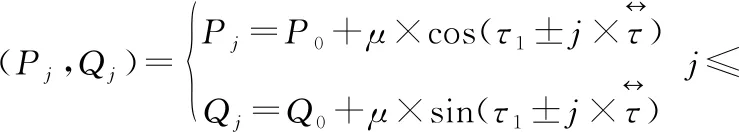
(7)

按照插补点坐标实现数控加工变形的圆弧运动补偿[13]。

在数控机床进行加工时，加工的工件出现变形时，误差补偿的目的是通过改变数控机床运行路径，使加工工件的误差实际位置回到理论位置上，从而保证加工的精度。在上述坐标获取基础上，给出插补点坐标，对同一坐标点，原坐标不变的情况下，可得到加工变形后数控机床应补偿的量为(Δx，Δy，Δz)，即：

(8)

2 实验分析

2.1 实验环境

为了验证所提方法的有效性，进行仿真实验分析。该实验选择某轴承厂生产的西门子840D/810D数控系统进行操控，实验操作系统选择Windows XP系统，CPU为Inter Pentium，8G内存，检测软件为Matlab 2019a。具体实验所用工件如图1所示。

图1 实验用工件

2.2 实验参数设置

为了验证所提方法的可靠性，实验参数设置如表1 所示。

表1 实验参数

在上述参数基础上，加工一个大小为50 mm×25 mm×6 mm的齿轮工件，比较所提方法、精确预拉伸方法以及扰动观测器的加工误差控制方法，实验指标为工件变形控制的误差率、误差补偿后的变形率以及控制的时间。为了保证实验的可靠性进行了多次验证。

2.3 实验结果分析

1)不同方法工件变形控制的误差率分析

为验证所提方法的可靠性，实验分析了所提方法、精确预拉伸方法以及扰动观测器的加工误差控制方法在进行工件加工时工件变形控制的误差率。其中，变形误差率越低效果越好。实验结果如图2所示。

图2 不同方法工件变形控制的误差率分析

分析图2可以看出，在相同情况下，采用三种方法控制数控加工变形的误差率存在一定差距。其中，采用所提方法进行控制的误差最低，始终低于2%以下，而其他两种方法的误差较高，相比之下，采用所提方法进行控制的误差率最低。这是由于所提方法采用多维度控制的方法，将数控机床进行加工时的运行轨迹进行多维度补偿，提高了控制的稳定性，验证了所提方法的有效性。

2)不同方法控制工件变形效果分析

为了验证所提方法的可行性，采用三种控制方法对实验用的工件变形进行控制。其中，与实验用工件吻合度越高，说明控制得越好。实验结果如图3 所示。

图3 不同方法控制工件变形效果对比

分析图3可以看出，采用三种方法控制数控机床加工工件的变形效果存在一定差异。其中，采用所提方法生产的工件与原始元件最为吻合，而其他两种方法控制加工工件变形程度较严重，均出现了不同程度的变形，相比之下，采用所提方法进行控制后的效果更佳，验证了所提方法的可行性。

3)不同方法误差补偿后的变形率分析

为了进一步验证所提方法的有效性，实验分析五种数控加工变形数据，通过三种方法进行加工控制，从直线运动补偿、圆弧运动补偿两个维度实现变形控制，实验结果如图4 所示。

图4 不同方法运动补偿效果对比

分析图4可知，三种不同方法对五种数控加工变形运行补偿后，与两种传统方法相比，所提方法应用后工件变形率更低。其中，当工件变形类型为折叠时，所提方法变形率低于2%，而其他两种方法均高于2%，验证了所提方法的有效性。这是由于所提方法针对工件加工进行直线和圆弧运动补偿，弥补了加工时工件变形的可能。

4)不同方法数控加工变形控制用时

为了测试所提方法在控制数控加工变形时的鲁棒性，实验分析了三种方法在数控机床进行加工时形变的控制用时，实验结果如表2所示。

表2 不同方法数控加工变形控制用时 单位：min

分析表2中数据可以看出，采用三种方法进行控制的用时存在一定差异。当迭代次数为3时，所提方法的控制用时为2.3 min，精确预拉伸方法的控制用时为4.7 min，扰动观测器的加工误差控制方法控制用时为3.7 min。相比可知，采用所提方法的控制用时最短，与另外两种传统方法相比，分别节省了2.4 min 和1.4 min，有效缩短了数控加工的工作用时。这是由于所提方法在多个维度上对数控加工形变进行处理，故有效缩短了控制用时。

3 结语

针对数控机床加工变形控制效果不佳的问题，提出基于多维度控制的数控加工变形控制方法。引入多维度控制方法，从不同角度对数控加工变形进行运行补偿，实现了数控加工变形控制。通过与传统方法相比，得到以下结论：

1)采用所提方法对工件变形控制的误差率低于2%，验证了所提方法的有效性。

2)采用所提方法控制工件变形效果更佳，生产的工件与理想工件更为吻合。

3)采用所提方法进行数控加工的运动补偿，工件变形类型为折叠情况下，所提方法变形率低于 2%。

4)采用所提方法进行数控加工变形控制的用时最短，最高为2.3 min。

综上所述，所提方法对数控加工变形控制的综合性能较好，是一种可行的数控加工变形控制方法。