基于ARIMA模型的地铁车门夹紧力预测
梁鑫,郑向东,仓恒,李宝林,高文科
(1. 兰州理工大学 能源与动力工程学院,甘肃 兰州 730000;2. 兰州轨道交通有限公司 机电设备处, 甘肃 兰州 730000)
0 引言
地铁车门是乘客上下地铁列车的重要通道,其系统工作的可靠性关系到乘客的安全和地铁的正常运营。由于地铁车门在不同站点频繁开闭,导致地铁车门系统的故障率较高。统计表明,在地铁车辆的各类故障中,车门系统部分故障占比可达40%[1]。因此,地铁车门系统的可靠性分析与研究对保障地铁的安全运营显得尤为重要。
地铁车门系统可靠性问题也引起了学界和企业界的广泛关注。李勃旭等[2]采用EMD-ARIMA模型对地铁车门夹紧力峰值进行分析,实现了对地铁车门系统的早期故障预测。CHENG Xiaoqing等[3]采用FMECA方法对地铁车门系统进行可靠性分析,分析结果有助于对地铁车门系统的维护。相对而言,以地铁车门夹紧力为对象分析车门传动系统状态的退化及预测方面的研究少有报道。
目前,地铁车门传动系统以丝杆传动居多。传动系统是车门系统中负责力和运动控制的执行机构,也是车门的重要组成部分。关于机械传动系统退化方面的研究,一直是学界和企业界关注的焦点。李苗苗等[4]利用ANSYS Workbench软件针对承受热应力和结构应力共同作用下的角接触球轴承进行疲劳寿命分析,分析结果为机床主轴轴承寿命的预测奠定基础。YAN J和LEE J[5]提出一种逻辑回归模型,运用极大似然法求解模型的参数,并基于模型所得的参数去评估系统可能发生的故障。不同学者基于传动系统性能退化参数对传统系统的剩余寿命进行了研究,由此可看出传动系统可靠性研究的重要性。
时间序列预测模型是利用观测的序列数据去预测未来变化趋势的一种数学模型。其中AR模型和MA模型是时间序列中较为简单的模型。ARMA模型是AR和MA两种模型的混合模型,针对平稳时间序列可以进行预测。针对非平稳时间序列须通过对原始时间序列进行平稳化处理,故引进了改进的ARMA模型,即ARIMA模型。ARIMA模型因具有良好的预测精度而被广泛应用于机械、能源和经济等不同领域。李琪和郝学军[6]运用ARIMA模型对燃气调压器出口压力进行预测,并通过已建立的故障诊断模式对燃气调压器进行了故障诊断。PENG Hongbo等[7]在经过处理的起飞EGTM数据的基础上,采用ARIMA模型对航空发动机的EGTM进行了预测。杨艺等[8]基于齿轮箱油泵出口压力SCADA的数据,采用ARIMA模型对齿轮箱的出口压力进行短期预测,进而分析齿轮箱的运行状态。
综上所述,鉴于地铁车门在地铁日常运营中的重要性,研究人员从不同角度对其可靠性和故障诊断方法进行了研究。同时,作为一种典型的机械传动系统,时间序列模型也在其变化趋势的预测方面有广泛的应用。此外,李勃旭等[2]前期采用EMD-ARIMA模型对地铁车门夹紧力的峰值进行预测,虽对地铁车门的维护有一定的参考,但仅从夹紧力峰值单项指标进行评估仍不够全面。因此,本文将地铁车门关闭过程夹紧力的变化波形作为研究对象,再考虑夹紧力相邻采集点之间的相关性,从两个维度运用ARIMA模型进行预测,实现对地铁车门夹紧力变化趋势的预测和分析。
1 ARIMA模型
本节主要从数据的平稳性检验、模型参数估计、模型检验和建模方法对ARIMA模型的建模过程进行介绍。
1.1 ARIMA模型介绍
ARIMA模型建模的基本思路:若原始数据是平稳的,直接选用ARMA模型进行建模;若原始数据不是平稳数据,则使用差分法对原始数据序列进行平稳化处理。通过观察p(AR阶数)、q(MA阶数)和d(差分阶数)这3个参数来进行模型的选取从而预测时间序列数据。ARMA模型的表达式为
yn=φ1yn-1+φ2yn-2+…+φpyn-p+εn-θ1εn-1-θ2εn-2-…-θqεn-q
(1)
将AR和MA模型结合经过差分形成ARIMA(p,d,q)模型,该模型的表达式为
∇dyn=φ1∇dyn-1+…+φp∇dyn-p+εn-θ1εn-1-…-θqεn-q
(2)
式中∇=1-B为差分算子,B为滞后算子,即Byn=yn-1,且φpθq≠0;同时{εn,n=0,1,2…}为白噪声序列,即E(εn)=0,var(εn)=σ2<∞,则称yn为自回归移动平均序列,记做ARIMA(p,d,q)。当|B|≤1时:
(3)
(4)
由式(3)-式(4)得
φ(B)(1-B)dyn=θ(B)εn
(5)
记φ(B)=φ(B)(1-B)d,则上式可写为
φ(B)=θ(B)εn
(6)
传统上述模型可以应用于一维时间序列问题的建模。针对地铁车门传动系统的退化不仅要考虑单点数据采集次数的维度,还要考虑同一次采集数据相邻两点间的时间维度,但传统模型在车门夹紧力的预测中忽略了对夹紧力相邻数据间相关性的考虑,故本文提出一种二维ARIMA预测法用于车门夹紧力的预测。
1.2 二维ARIMA预测方法
原始数据相邻两点之间存在递增或递减的约束关系,基于此本文采用二维预测的方法分别从单点和斜率两个方面对原始数据进行分析。基于ARIMA模型的车门夹紧力二维预测法是获取车门夹紧力数据列后,再通过差分对原始数据列做平稳化处理,最终运用ARIMA模型对车门夹紧力进行预测。主要步骤如下:1)获取原始数据并对原始数据进行平稳性检验,若数据不满足平稳性条件则对数据进行差分,一直差分到满足平稳性条件为止。2)数据列平稳后,计算数据列的相关系数。3)ARIMA模型参数估计,ARIMA模型包含p、d、q三个参数,其中d的估计比较简单。对原始数据列进行平稳性检验,若不满足平稳性条件则需进行差分,一直差分到满足平稳性条件即可,此时经过的差分阶数就是d的值。若一直达不到平稳条件则不适用于ARIMA模型。参数p和q的确定则需根据PACF(partial auto-correlation function)图和ACF(auto-correlation function)图进行确定。4)采用QQ(quantitle-quantitle)图对残差进行检验,数据靠近45°线则模型适合预测,否则需重新选取模型。5)利用已通过检验的模型对数据进行预测,最后把单点预测输出的数据和斜率预测输出的数据求算术平均值作为最终预测值输出。二维ARIMA模型建模流程图如图1所示。
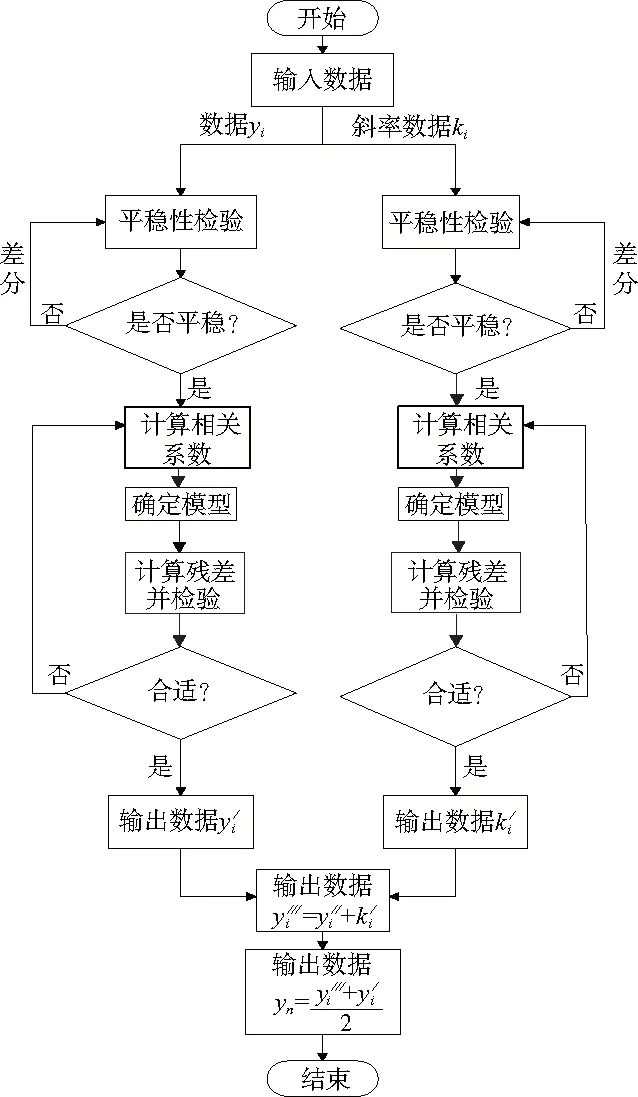
图1 二维ARIMA模型建模流程
2 地铁车门夹紧力预测
本节分别从地铁车门传动系统和地铁车门夹紧力数据建模两个方面展开介绍。
2.1 地铁车门传动系统概述
地铁车门传动系统主要由基架、丝杆、驱动装置、长/短导柱、携门架、LS型锁闭装置、端面解锁装置与行程开关组成。其中基架为其他部件的安装提供基础;丝杆是车门系统实现开关门动作的动力传递部件;驱动装置是实现车门开关动作的动力来源;长/短导柱为车门横、纵向移动提供自由度;携门架将门扇的所有质量和动力传送给长导柱;LS型锁闭装置应用自锁原理实现门机的锁闭与无源自解锁;端面解锁装置负责丝杆的解锁;行程开关负责控制车门的开关。地铁车门传动系统工作原理可简述为:当地铁到站开门时,驱动电机通过相关连接装置带动丝杆及与其配合的螺母锁闭装置,进而带动携门架等导向部件动作,并最终使得车门通过短导柱向外摆出。当车门完全向外摆出后,车门将通过长导柱向左右两侧作平行于车体的平移运动,直至车门门扇完全打开并与缓冲头相接触。关门动作则与上述过程完全相反。工作原理简图如图2所示。

图2 地铁车门结构示意图
在地铁车门关闭的行程中,取左门扇作受力分析,受力分析图如图3所示。

图3 车门受力分析图
分析可得传动系统传递到车门上的力F(t)与地铁车门打开方向的平衡方程如下:
(7)
(8)
(9)
式中:F(t)为传动系统传递到车门上的力;p为轴传递的功率;n1为电机轴的转速;Z1为小齿轮齿数;Z2为大齿轮齿数:η为丝杆传动效率,0.9~0.95;Ff为地铁车门单个门扇在打开或关闭的过程中摩擦力;L为地铁车门单个门扇的最大行程;l为弹簧自由长度,即弹簧未受力时的长度;x(t)为单个门扇在关门过程中的位移量;m为单扇车门的质量;Ft(t)为弹簧弹力。
由上述方程式可知,实际采集到的车门夹紧力Ft(t)将在[L-l,L-h]行程段,并与车门运行过程中摩擦力Ff、传动系统传递到车门上的力F(t)有关。而从式(7)可以看出,F(t)与齿轮齿数、电机转速、轴的传递功率等因素有关。在传动系统中,这些参数的变化会直接导致F(t)的变化,并相应地引起所测夹紧力Ft(t)的变化。其次,随着地铁运行时间变长,车门开关次数越来越多,车门传动系统将会产生机能退化,例如丝杆、长/短导柱的磨损等。这些机能退化将引起摩擦力Ff的变化,从而也会引起夹紧力Ft(t)的变化。故通过夹紧力测量装置测得的夹紧力数据可在一定程度上反映车门传动系统的退化状态。因此本文选取地铁车门夹紧力Ft(t)为研究对象。
2.2 建模过程
本文把在某地铁公司运行一段时间的某型号地铁车门采集的夹紧力作为研究对象,展开地铁车门夹紧力的预测研究。一维预测首先将采集到的地铁车门夹紧力数据作为原始数据yi进行平稳性的检验,检验结果h=0则进行差分。进行一次差分后h=1,此时d=1。下一步根据差分数据列计算得出的自相关系数(ACF)和偏自相关系数(PACF)暂定模型参数p和q,不断对模型调节参数进行拟合,最终确定ARIMA模型(p,d,q)。二维预测获取地铁车门原始数据列相邻两点之间的斜率,把获取的斜率数据作为二维预测的原始数据ki输入,重复上述建模过程,预测斜率数据输出后,将斜率预测获得的数据y‴与一维预测获得的数据y′求算术平均值作为最终的预测结果yn输出。
3 案例分析
本文采用已有的采集装置对某地铁公司运行一段时间的地铁车门夹紧力进行数据采集,每隔2周采集1次数据。前8次数据为现场采集数据,后5组数据均由插值获得。在已有13组夹紧力数据的基础上,采用已通过检验的ARIMA模型,分别从单点和斜率两个方面对地铁车门夹紧力进行预测,并采用二维预测的方法对地铁车门夹紧力进行5步预测。5步预测结果如图4所示。

图4 5步预测结果
从图4中可看出,在5步预测中,二维预测曲线与原始曲线的走势一致,说明二维预测法对于车门夹紧力的预测是可靠的。为了验证二维预测法在多步车门夹紧力预测的可靠性,又分别对车门夹紧力做了10步和15步的二维预测。预测结果如图5-图10所示。
通过图5-图10的对比可知,二维预测曲线与原始曲线的重合度比一维的好。为了验证这一观点,对此预测结果进行多角度评估,评估指标如下。

图5 第18步的一维预测
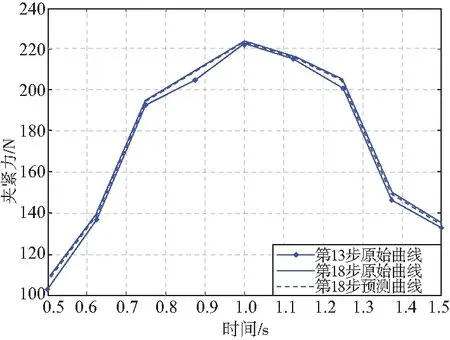
图6 第18步的二维预测

图7 第23步一维预测
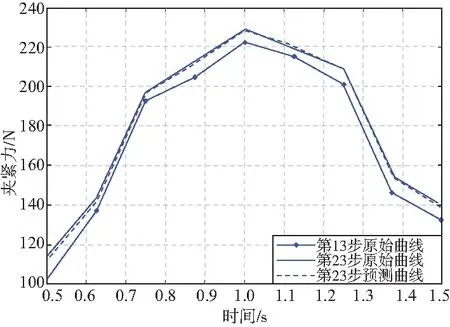
图8 第23步二维预测
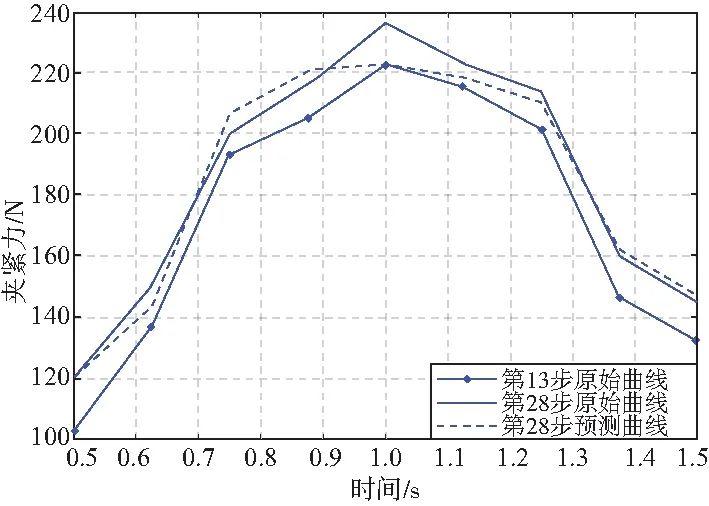
图9 第28步一维预测

图10 第28步二维预测
平均绝对误差:
(10)
平均相对误差:
(11)
预测均方差:
(12)
式中:yi为真实值;yn为预测值。MAE、MRE和MSE计算结果分别如表1所示。由表1可知二维预测曲线的MAE、MRE和MSE均小于一维预测曲线,进一步说明二维预测曲线与原始曲线的重合度更高。
从图5-图10可以看出,因为地铁车门夹紧力也受到预测精度和其他一些因素的影响,预测出的夹紧力数值不可能与真实的夹紧力数据完全一致,所以采取了误差分析。对预测后的夹紧力数据和真实夹紧力数据进行误差计算,分析计算结果是否在允许的误差范围内。在工程上,误差在原始数据5%以内是可以接受的。误差图如图11-图13所示。
由图11可知,第18步的二维预测误差小于一维预测误差,且由表1可知二维预测曲线的MSE值小于一维预测曲线。由此可知,在第18步的曲线预测中二维预测精度高于一维预测精度。

表1 MAE、MRE、MSE值
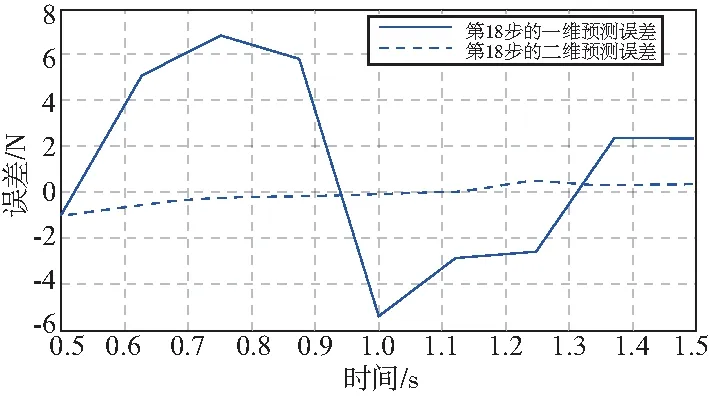
图11 第18步的预测误差
由图12可知,第23步的一维预测误差最大值为8.6,二维预测误差最大值为2.1。由此可知,二维预测曲线的精度高于一维预测曲线。

图12 第23步的预测误差
由图13可知,一维第28步预测误差图中,第5个点的真实值为236,预测值为222.4,其误差的绝对值达到13.6,其误差已超出可接受范围。综上所述,二维预测精度比一维预测精度高。
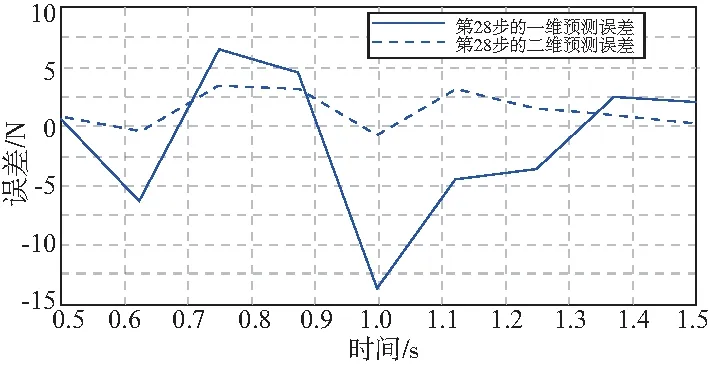
图13 第28步的预测误差
4 结语
本文以地铁车门夹紧力为研究对象,采用ARIMA模型的二维预测法对地铁车门夹紧力进行了预测。通过对预测数据和实际数据之间的对比,得出以下结论:
1)采用ARIMA模型用二维和一维预测方法分别对地铁车门夹紧力进行了5步、10步和15步预测,结果表明在同等步长下,二维预测曲线与原始曲线的拟合度高于一维预测曲线。
2)采用ARIMA模型的二维预测法相比一维预测法在预测精度方面得到了提高。同时,二维预测法的预测步长高于一维预测法。
3)采用ARIMA模型实现了对地铁车门夹紧力曲线的预测,预测结果可为地铁车门系统的故障诊断提供支持。

