城市轨道交通多普勒雷达测速算法研究

王强，史学森，詹洁，张子龙

(1. 中国电子科技集团公司第十三研究所，河北 石家庄 050051； 2. 北京理工大学 信息与电子学院，北京 100081； 3. 北京中电科卫星导航系统有限公司，北京 100040)

0 引言

城市轨道交通系统具有运量大、占地少、单位运量能耗小等诸多优点，成为世界各国交通建设的重点[1]。随着以高铁和地铁为代表的轨道交通系统的快速发展，轨道交通车辆的速度检测作为列车运行控制系统的关键技术之一，是列车安全保障体系的重要组成部分[2]。实时、准确地获得列车速度是列车安全高效运行的重要保障。随着列车运行速度的不断提升，对列车测速的精度及可靠性也提出了更高的要求[3]。

比较常用的测速方法有列车转轴转动测速、GPS(global positioning system)导航定位测速和雷达测速[4]。转动测速是一种直接接触式的测量方法，结构简单，测量误差较大。GPS导航测速是一种非接触式的测量方法，利用GPS卫星定位实时获得列车的运行速度，受天气及环境影响较大。雷达测速也是一种非接触式测速方法，根据多普勒效应，通过测量多普勒频率差，得到列车的运行速度信息。雷达测速在测速原理、精度及可靠性方面的优势使之更加适合对高速列车进行速度测量，特别是随着微处理器技术的飞速发展，雷达测速技术在列车测速领域具有广阔的应用前景。雷达测速的原理是根据列车的运行与发射信号之间的多普勒频差，解算出列车运行速度信息。因此，高精度频偏估计方法是雷达测速的关键技术之一。

频偏估计方法大致可以分为时域估计法和频域估计法。时域法存在较高的信噪比门限，适用于高信噪比条件，而频域法的信噪比适用范围和频偏估计范围均较时域法广，因此得到了广泛的应用[5]。频域估计法基于信号周期图，通常先利用傅里叶变换获得信号的频谱峰值信息，再利用频谱矫正技术对初始估计的频率进行修正。由于能量泄露和栅栏效应，频率估计值与实际频率值存在较大误差，因此众多学者研究了各种频率校正算法。常见的主要有插值法[6]和能量重心法[7]。插值法的估计精度受到频率真实谱线位置分布的影响，估计性能不理想。能量重心法是以周期图频率粗估计为基础，根据加窗后信号功率谱的能量重心逼近主瓣重心的特性，对信号频率峰值进行修正。实际中，信号叠加噪声会干扰谱线的正确选择，从而影响能量重心法频率矫正的精度[8]。因此通过优化谱线选择可以有效提高频率估计精度。另外，学者们还把自相关技术应用到频率修正算法中[9-11]，提高了现有信号频偏估计的精度。在前人研究的基础上，针对现有的基于能量重心法在频率修正方面存在的局限，本文对能量重心法进行改进，并采用自相关处理来抑制噪声，提高频偏估计的精度。

1 多普勒雷达测速原理

1.1 系统组成

多普勒测速雷达通过检测多普勒频移完成对目标运动速度的检测，其主要由信号处理单元、基带、射频发射接收单元、天线和接口电路(串口)等构成，系统原理框图如图1所示，测速雷达实物图如图2所示。基带和射频发射接收单元主要产生一定频率的微波信号，并由天线将这个信号定向发射出去，同时对于反射回来的信号进行接收、混频等；信号处理单元主要完成基带信号的处理，以便获得能反映目标真实运动的多普勒频率；接口电路按照使用要求将获得的目标运动速度信息送出。

为获得稳定可靠的多普勒频率，本系统在一部雷达上集成两个不同角度的多普勒测速模块。通过提取轨道方向的分量进行各自处理，得出最终的结果。即使某一个模块出现了问题也可以保证测速正常，能够有效提高产品的可靠性。

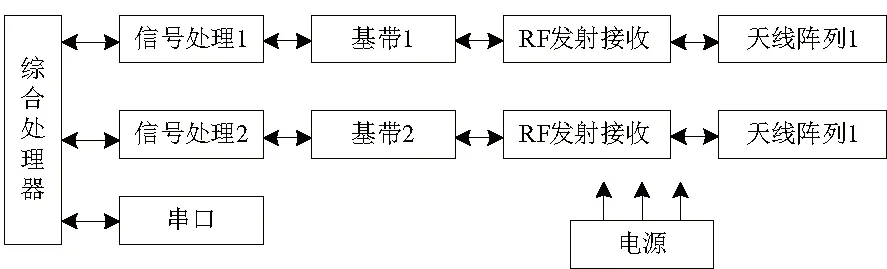
图1 多模块雷达测速原理框图

图2 测速雷达实物图

1.2 雷达测速算法原理

雷达测速的原理是利用多普勒效应对目标速度进行测量，如图3所示。当目标与雷达存在相对运动时，会产生多普勒频移，而目标的速度大小可通过多普勒频移计算得到，计算公式为

(1)

其中：fd为多普勒频移;λ为雷达波的波长;φ为雷达天线与地面的夹角。从公式(1)可知，提高频率估计精度可以有效提高雷达测速精度。

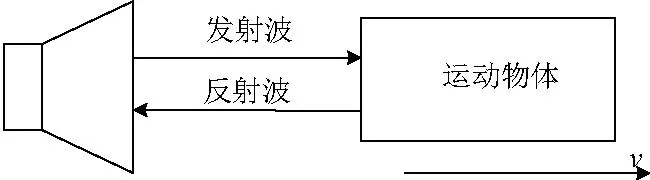
图3 多普勒效应示意图

2 基于自相关和改进能量重心法的频偏估计算法

设信号模型为单频复正弦信号，对信号进行采样截断后得

x(n)=Aexp(2πf0n/fs+φ0)+nr(n)

(2)

其中：A为信号幅度；f0为信号频率；fs为采样频率；信号功率Es=A2；nr(n)表示复高斯白噪声，其实部和虚部的均值为0、方差都是σ2，所以复噪声功率为N0=2σ2，信噪比(SNR)为Es/N0=A2/(2σ2)。对信号进行N点傅里叶变换变换得

(3)

其中Ts为采样周期。频谱分辨率为Δf=fs/N，X(k)幅值最大处谱线的索引记为kmax，kmax是最接近信号频率真实值的谱线。由于信号截断引起的能量泄露和采样引起的栅栏效应，不可避免地导致估计精确度受限。利用频谱矫正技术计算修正因子δ进行补偿，可以得到矫正后频率估计值为

(4)

其中修正因子δ的实际物理意义是：信号实际频率f对应谱线的位置相对于幅度峰值谱线kmax的偏差，并且有-0.5≤δ<0.5。

2.1 自相关处理

根据信号与噪声之间的相关特性可知，对信号进行自相关预处理，可以有效抑制噪声，提高信噪比，从而提高信号的频率估计精度[12]。对信号进行自相关预处理后的自相关函数可以表示成[13]

(5)

其中l表示相对时延。从上式可以看出，自相关函数包含了信号的频率和相位信息;φl表示零均值相位噪声，其概率密度分布函数为：

p(Δφ|χ)=

(6)

其中χ=A2/2σ2表示信噪比。x(n)的自相关序列表示为[14]：

Rxx(l)=Rss(l)+Rsz(l)+Rzs(l)+Rzz(l)

(7)

其中:Rss和Rzz分别是正弦分量s(n)和余弦分量z(n)的自相关函数;Rsz和Rzs分别是s(n)和z(n)的互相关函数，z(n)是随机噪声，和s(n)没有相关性。

当N足够大时，则s(n)和z(n)的自相关函数分别为：

Rzz(l)=σ2δ(l)

(8)

(9)

近似有：

(10)

所以Rxx(l)可以写成

(11)

综上分析可见，对信号进行自相关预处理，可以有效抑制噪声，提高信号处理的信噪比，从而提高频率估计性能。

2.2 改进的能量重心法

能量重心法是根据信号功率谱的重心逼近主瓣重心的特性为基础，对频率估计值进行修正的方法。设G(k)为信号的功率谱，有

G(k)=|X(k)|2/L

(12)

其中L为自相关参数。

设δECC为能量重心法计算得到的频率修正值，则有

(13)

由能量重心法计算得到的修正值与谱线的选取有关，当真实频率接近量化频点时，估计精度较高，当真实频率接近量化频点中间位置时，估计精度较低。对此文献[8]提出了一种改进算法，记为ECC_m。该算法在峰值谱线左右各增加一条谱线用于计算修正值，方法如下：

(14)

其中δl和δr分别为峰值谱线左侧和右侧增加一根谱线计算得到的修正值，R(±1)=Re[X(kmax±1)X*(kmax)]为谱线之间幅角相位差的余弦值。

能量重心法的精度不仅与谱线选择有关，还与频偏真实值的分布有关[14]。当真实频率与峰值谱线对应的频率差位于区间[-0.2, 0.2]，采用奇数根谱线能量重心法获得的估计精度较高，而位于<-0.2和>0.2的区间时，增加一根谱线来获得修正值可以提高频率估计精度。

所以本文对能量重心法进行改进，基于改进的能量重心法的频率估计算法描述如下：

1) 对采样后的接收信号进行自相关预处理；

2) 利用周期图法得到频率的粗略估计值；

3) 采用常规能量重心法计算频率修正值δo；

4) 根据δo的所在区间获得最终的频率估计结果。当δo位于[-0.2, 0.2]区间上时，则直接采用δo作为信号频率估计的修正值。当|δ0|≥0.2时，如果δo的符号为正，增加一根峰值谱线右侧的谱线计算得到δr的值作为信号频率修正值，如果δo的符号为负，增加一根峰值谱线左侧的谱线计算得到δl的值作为频率修正值。

3 仿真验证

本文通MATLAB软件对所提算法的频偏估计性能进行Monte-Caro仿真，并与现有基于能量重心法的频偏估计算法进行比较，实验次数为2 000次。采用修正克拉美罗界(MCRLB)作为频偏估计参考指标，其表达式为[5]

(15)

其中χ为接收信号的信噪比。设置接收信号采样频率fs为60 MHz，数据长度为1 024点，自相关参数为512，对自相关序列R(l)进行512点FFT运算。

对改进后的能量重心法在不同条件下的性能进行仿真验证，并与常规能量重心法进行比较。所有算法均进行自相关预处理，仿真结果如图4所示。ECC_tra为常规能量重心法，ECC_left和ECC_right分别为峰值左侧和右侧增加谱线的改进型能量重心法。仿真结果表明，随着信噪比的增加，频率估计精度所有提升。常规算法在区间δ=[-0.2,0.2]的估计精度最高，峰值左侧增加谱线法在区间δ>0.2时的估计精度最高，而峰值右侧增加谱线法在区间δ<-0.2时的估计精度最高。

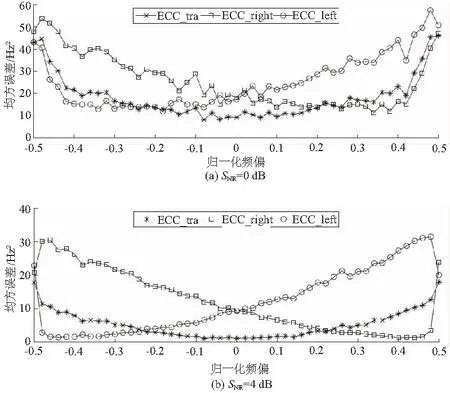
图4 谱线选择对能量重心法精度的影响

图5 不同δ条件下的频偏估计精度

对所提算法在不同信噪比条件下的估计性能进行仿真，常规的插值法(IC_tra)和ECC_m算法进行比较，所有算法均进行自相关预处理，仿真结果如图6所示。在此取仿真的频偏区间为[-4δ,4δ]，并对频率的均方误差关于δ取平均。仿真结果表明，随着信噪比的增加，信号的频率估计性能有所提升。所提算法的平均估计性能优于另外两种算法，尤其在低信噪比条件下，所提算法相较于插值算法的优势更加明显。

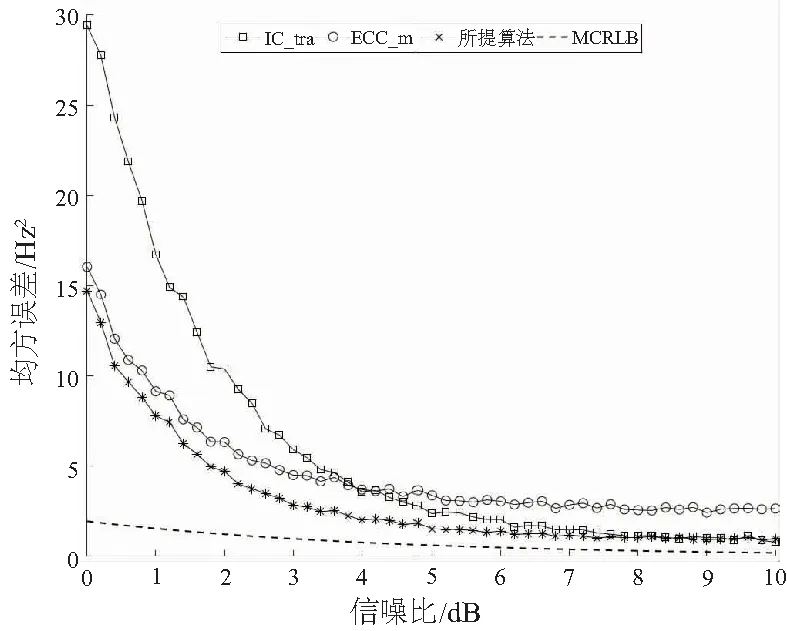
图6 不同信噪比条件下的频偏估计平均精度

由于3种算法均进行傅里叶变换运算和自相关处理，在运算量上的差异仅体现在对修正值的计算，修正值计算的运算量相比于自相关处理和傅里叶变换运算占比很小，所3三种算法的运算量在一个量级上。能量重心法通过功率谱计算修正值，运算量比插值方法略大，而所提算法的运算量与常规改进的能量重心法相比运算量相同。

4 结语

多普勒雷达测速可实现对列车运动速度的高精度测量，而频偏估计算法的性能对雷达测速的精度至关重要。本文提出了一种基于自相关预处理和改进能量重心频谱矫正的频偏估计方法。采用自相关处理进行噪声抑制，然后利用改进的能量重心算法对多普勒频偏进行估计。最后通过仿真对所提算法进行了仿真验证。结果表明：所提算法比常规算法具有更好的频偏估计性能。目前该算法被成功应用到西安、长沙等地铁项目的测速设备中，有效提高了测速的精度。