港口流动机械转向系统的优化及应用
凌君安, 陈 燕, 陈 康
(长沙君祥科技有限公司, 湖南 长沙 410100)
0 引言
港口集装箱的装卸除了由场桥、岸桥、门座起重机等大型起重设备完成之外, 还有相当一部分的装卸作业是由流动机械完成的。 港口流动机械主要用于集装箱的搬运、堆垛,典型设备如正面吊运机、空箱堆高机、重叉、仓储叉车等。 港口流动机械不仅能够吊运重达几十吨的重箱,还能同时堆垛两个空箱,机动性较强,换向频率较高,如何设计一套安全合理的转向系统则尤为重要。 鉴于港口流动机械多为前轮驱动,后轮转向,本文主要讨论后桥转向桥的优化设计方法。
1 转向桥简介
港口流动机械多采用液压式横置油缸式转向机构,主要由转向桥梁、转向油缸、转向节、连杆、转向销轴、轮胎等组成,结构如图1 所示。该转向机构具有转向角度大、转向一致性好、维修方便等优点[1]。

图1 转向桥结构示意图
2 转向桥的优化目标
转向桥的优化目标:①保证较高的机动性,在有限的场地面积内具有迅速和最小转弯能力, 即最小转弯半径要小;②保证转向时,轮胎做纯滚动,即全部车轮绕一个瞬时转向旋转,降低轮胎磨损程度[2];③优化油缸的受力,降低转向过程中,转向油缸承受的轴向力和径向力,通过减小径向力和径向弯矩来降低油缸漏油故障率, 同时通过减小轴向力来降低油缸缸径/杆径的尺寸; ④减少转向时打方向盘的圈速,降低驾驶时的疲劳感。
2.1 最小转弯半径
本文所指的最小转弯半径[3]是最小外侧转弯半径,即空载时打满方向盘后将转向轮置于极限转角位置, 并已最低稳定速度行驶时, 整车瞬时中心距车体外侧最远点的距离。 考虑到本文是对后桥进行优化,不涉及车架体,为便于进行对比, 取后桥轮胎压痕的中心作为最小转弯半径,如图2 所示,并满足如下公式:

式中:R—最小转弯半径;L—轴距;M—主销距;m′—轮距;α—外转角;β—内转角。
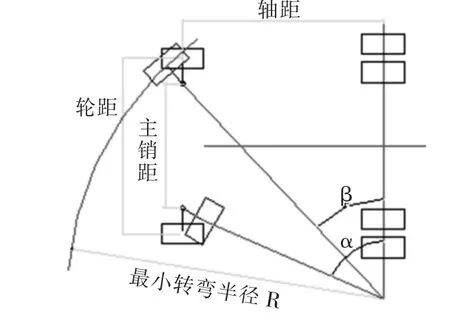
图2 转角示意图
2.2 轮胎磨损
轮胎磨损除了与其承受的载荷及作业场地的静、动摩擦系数有关之外, 还与在转向过程中是否做纯滚动有关。所谓纯滚动即转向过程中,所有车轮的轴线延长线都时刻相交于一点, 且各个车轮的转速与各车轮至转向中心的距离成正比,即满足如下公式:

如果转弯时左右转向轮不是绕一个点作纯滚动,而是绕相距很远的两个不同点转动,就会导致轮胎侧滑,加剧轮胎磨损。然而实际过程中,转向轮是不会时时刻刻都做纯滚动的, 实际上的转向角与理论上的总是有点偏差,我们将这个偏差作为衡量轮胎纯滚动的指数。 偏差值越大,指数就越低,轮胎发生偏磨的可能性就越大,因此降低理论与实际上的转向角偏差也是转向优化的目标之一。
2.3 油缸受力优化
油缸受力优化主要是指优化油缸活塞杆所承受的轴向力和径向力。 转向油缸中液压油的转向压力主要是由负载决定的,如果总的轴向力过大,在缸径、杆径不变的情况下,势必会增加转向油压的压力。转向压力升高一方面会增加主液压泵的负担, 另一方面还会导致转向油缸漏油故障。 除此之外,如果活塞杆承受的径向力(径向弯矩) 较大, 压坏了导向套或者使活塞杆产生大的挠度变形,也会导致漏油故障甚至活塞杆断裂等严重故障。只有油缸所承受的轴向力和径向力都降低了, 才有可能适当缩减油缸缸径、杆径尺寸,使得后桥看起来更轻便化。
2.4 减小转向圈速,提高驾驶舒适性
这里所说的驾驶舒适性具体指在转向时,沿方向盘的切向力要小,同时转向的圈速也要小。虽然转向时打方向盘的切线力与转向器有关,与后桥转向机构无关,但是转向圈速却与后桥有关, 主要是与转向时流过转向油缸液压油的体积有关,即转向油缸的缸径、杆径及行程有关[4],并有如下公式:

式中:V—转向油缸的有效容积;q—转向器排量;n—方向盘的最大转向圈速;ɑ—从转向器马达到转向腔的容积效率。

式中:D—缸径;d—杆径;S—油缸行程。
通过优化油缸受力,在满足零件材料强度的条件下,降低油缸活塞杆承受的径向力来缩减杆径, 同时降低轴向力来同比例的降低油缸缸径, 进而减小转向液压油的体积,达到减小圈速的目的。
在上述四个目标的优化过程中往往会出现以下情况, 比方说为了降低最小转弯半径, 势必会增大油缸行程,导致油缸轴向力和径向力加大,还有可能增加转向圈速; 将主销靠近轮胎, 可以减小轮胎的转向阻力距的力臂,降低轴向力,但会影响到轮胎的存滚动性和最小转弯半径, 也就是说以上四个优化目标具有不一致性性和非线性,在对一个主优化目标优化的时候,就必须限制其他优化目标的范围, 因此这是一个多变量多目标多约束的优化设计问题。
3 优化设计方法
在转向桥的优化设计过程中, 通常已给定了整车的轴距(L),轮距(m′),最小转弯半径(R)三个参数,以上三个参数是在产品总体设计时就定下来了的。 需要我们优化设计的是主销距(M),活塞杆长(l),油缸的左右行程(S),转向节与连杆铰接处的位置参数等。
针对这种多目标多约束的优化设计问题, 本文采用的是基于ADAMS 的参数化建模方法[5]。 参数化建模即先简化转向桥模型,建立转向机构杆系模型,如图3 所示,将以上6 个铰接点的横、纵坐标设计成变量,考虑到转向机构模型的对称性,共设有5 个独立变量。根据各构件关系建立约束副, 活塞杆与地面建立移动幅, 其他为旋转副;加载转向阻力矩;创建传感器Sensor-1,即当最小转弯半径满足要求时停止优化仿真;定义运动:在活塞杆中心处创建沿轴向的直线运动Motion-1;建立测量,有“内转角、外转角、活塞杆左端x 向力、活塞杆左端y 向力、理论内转角、理论外转角与实际内外转角之差”等。 通过优化转向机构,使得轮胎纯滚动指数更高,并优化轴向力及径向力,满足上述所提到的优化目标。详细步骤及参数如表1 所示。
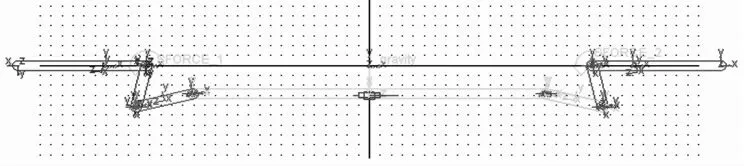
图3 转向机构ADMAS 模型图
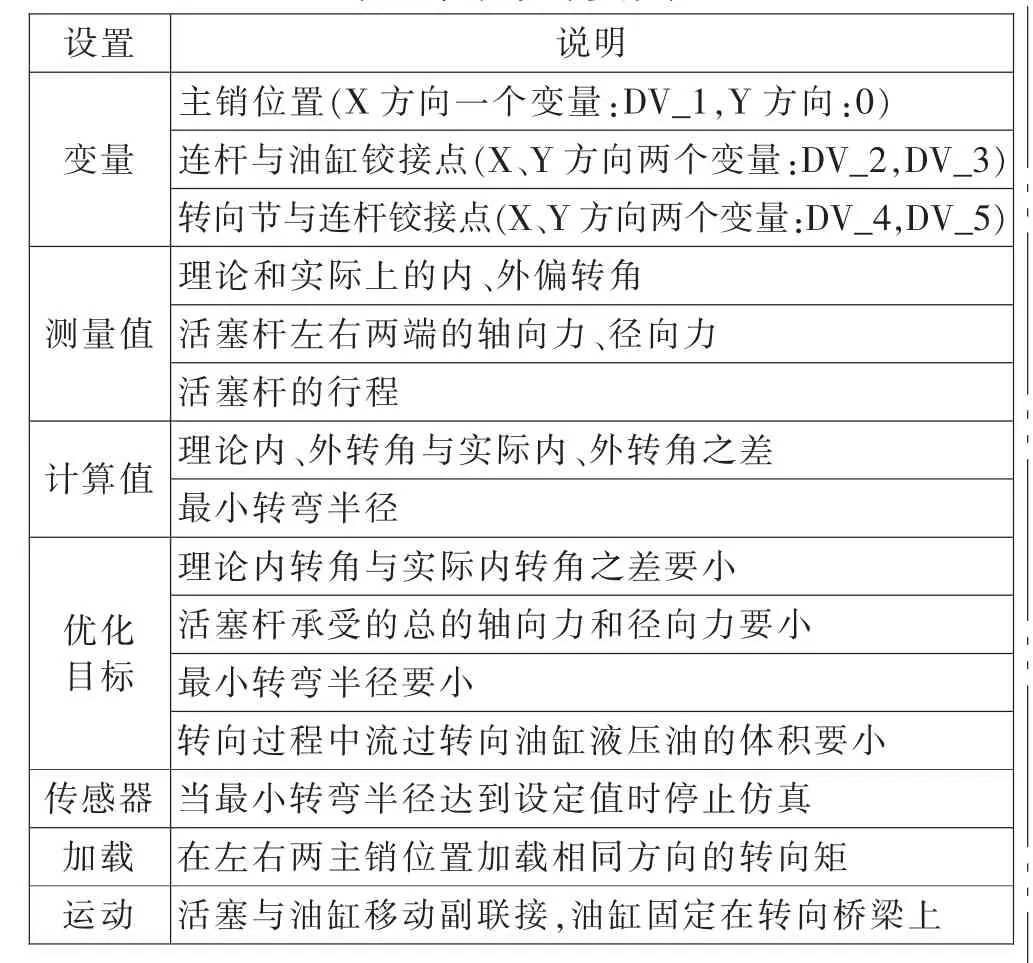
表1 优化设计参数表
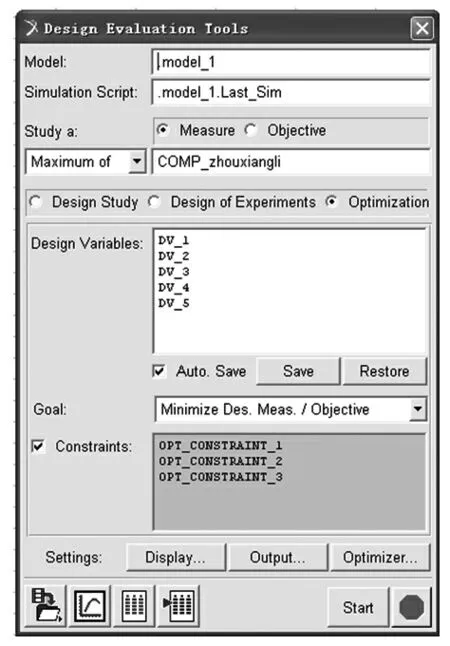
图4 ADAMS 多目标优化界面
图4 为ADAMS 多目标优化界面,我们取轴向力为主优化目标,图4 中研究的是轴向力(COMP_zhouxiangli)的最大值,其目标是使其最小化;约束函数则代表其他优化目标, 并给定了一个限制范围, 比方说将OPT_CONSTRAINT_1 设定为转向角的最大偏差值 (绝对值) 小于0.5 等。 点 击START 之后,ADAMS 就会自动迭代计算, 当满足优化条件后就会自动弹出每个参数的具体值, 这几个数值便是转向机构的铰接点位置, 有了这几个位置就可以进行三维模型设计了。 为了避免干涉, 还需对转向桥三维模型进行机构仿真,并利用PROE 的回放功能,检查有无干涉现象,当有干涉时,会出现红色阴影区或者停止仿真,见图6。
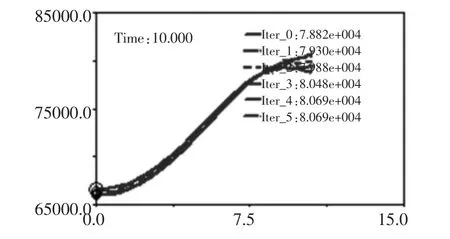
图5 迭代运算界面
图6 机构仿真中的回放界面
4 应用
现举我司一台流动机械为例。 主机轴距L=4550mm,后桥轮距m′=2150mm, 原后桥转向机构的铰接点位置分别为:DV_1=825,DV_2=598,DV_3=-150,DV_4=598 ,DV_5=825,通过上述提到的ADAMS 多目标多约束优化方法,优化后得出:DV_1=959,DV_2=725,DV_3=-169,DV_4=1008,DV_5=-239, 各个优化目标的优化情况如图7~图12 所示,其中红色虚线代表改进前,蓝色线代表改进后。从图7中可以很明显看出轴向力是大大降低了, 由原来的8.92吨力降低为7.1 吨力,下降了19.3%。 图8 为径向力的优化前后对比图,径向力由2.44 吨力降低为2.02 吨力,下降了17%。 图9 为连杆受力的对比图,连杆所受的最大力由原来的5.44 吨力下降为4.45 吨力,下降了18.2%。 图10 为最小转弯半径,优化前后相当。 图11 为内角偏差值的优化情况,之前最大偏差角度为1.62°,优化后仅0.5°。 图12为外角偏差值的优化情况,由之前1.21°降低为0.38°,轮胎存滚动性得到极大的提升,大大降低了轮胎发生偏磨的机率。 同时由于油缸所受的轴向力和径向力大大降低,我们也适当降低了油缸的缸径和杆径,并算出了改进后转向油缸的容积下降了15%, 即转向圈速会降低15%左右。
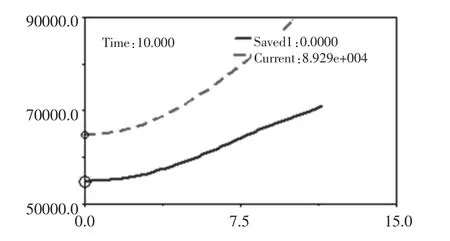
图7 轴向力优化前后对比
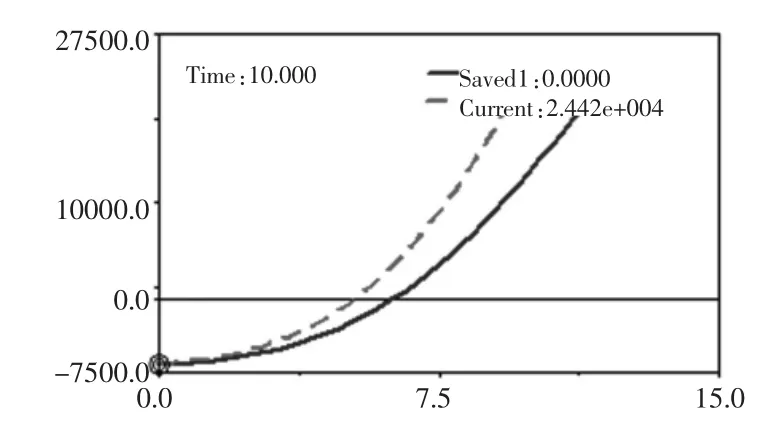
图8 径向力优化前后对比

图9 连杆受力优化前后对比

图10 最小转弯半径优化前后对比
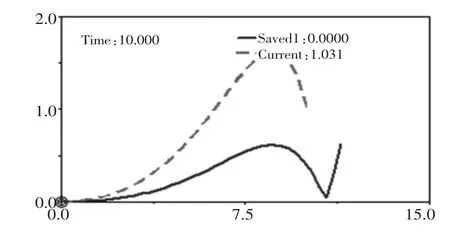
图11 内角α 偏差值优化前后对比
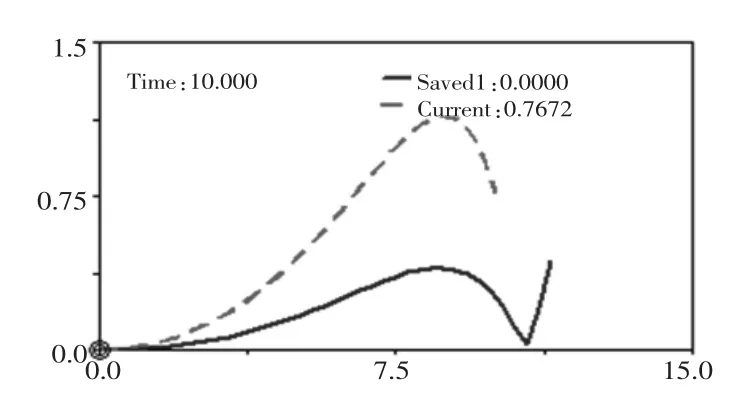
图12 外角β 偏差值优化前后对比
通过测量转向油缸中油口的压力, 得出优化前与优化后的转向压力相当,说明轴向力的的确确是降低了。 另外转向圈速也由原来的4.5 圈变为4 圈,验证了上述优化方法的可靠性。 最小转弯半径(后轮压痕中心)由原来的5866 变为5870,满足主体设计要求。
5 结束语
转向桥的优化设计问题, 是一个多参数多目标多约束的优化设计问题。 本文通过建立转向桥的ADAMS 参数化模型, 并对其优化设计,达到了降低油缸所受的轴向力和径向力,提高轮胎纯滚动指数、缩减方向盘转向圈速的目的,测试数据也表明轴向力和转向圈速的的确确是降低了,验证了本文所述的方法是进行转向桥优化设计行之有效的方法,同时针对其他工程领域中的多参数多目标多约束问题的求解也具有较强的指导意义。

