表贴式永磁电机转子无铁心解析法磁场分析
陈 中,刘丹丹
(盐城工学院,盐城 224051)
0 引 言
永磁电机的发展与贡献在现代工业领域已成为无可争议的焦点,无论在普通家用电器、医疗器械,还是航空航天等领域总能发现永磁电机的身影。国家2025规划纲要明确提出,提升工业自动化的升级换代,加大在新能源领域的基础设施建设,建设智能化节约型的现代化国家。结合永磁电机本身的特点,一般常将其分为:表贴式、表面插入式、埋入式。每一类电机都有着各自的特点,表贴式电机多用在伺服控制领域,其转子形状的特点并不会引起电感在直交轴分量的参数变化,便于电机的精确控制。对表面插入式电机以及埋入式电机,由于转子磁路在物理空间上的非对称性,转子在旋转过程中会引起电枢绕组中电感在直交轴上的分量发生变化,并且会产生磁阻转矩,故在高功率密度电机应用场合被广泛应用,如电动汽车领域。
结合磁钢材料的发展,加工工艺的完善,从之前的铁氧体材质,到现在的钕铁硼的广泛应用,给永磁电机行业带来生机活力。永磁材料充磁方式也多种多样,常见有径向、平行、Halbach、正弦等。其中径向充磁可产生梯形波的反电动势,平行、Halbach充磁可获得近似正弦波的反电动势;正弦充磁可获得较理想的反电动势波形,但在实际充磁过程中需要的技术条件也往往比较高。因此,结合电机驱动器电流波形的特点,在无刷直流电机领域,一般采用径向充磁;而在永磁同步电机领域,一般采用平行充磁,Halbach与正弦充磁在实际应用中需要的充磁设备条件较高。
文献[1]采用解析方法对径向、平行充磁进行了充分研究,但针对的是转子有铁心的结构。文献[2]采用解析方法对转子磁极形状设计作了详尽分析,指出转子中注入三次谐波可提高电机转矩输出能力,同时也会带来转矩脉动增大的问题,但也是针对转子有铁心结构。文献[3-4]借助解析方法,针对有铁心结构的转子磁极不等厚永磁采用Halbach阵列作了研究,指出Halbach充磁方式可有效提升气隙磁密波形的正弦度,降低谐波含量。文献[5-6]主要对梯形结构永磁在无铁心盘式电机轴向磁场进行分析,指出梯形结构永磁在盘式电机可减小永磁的利用,增大气隙磁密中的基波幅值,削弱磁场中的谐波含量。文献[7]只采用有限元法对转子有铁心和转子无铁心结构进行了分析,指出转子有铁心结构相对无铁心结构,可降低电机的铁耗,提升电机的效率,但并未采用解析法进行分析。文献[8-11]对表贴式永磁电机解析法分析了空载气隙磁密与反电动势的关系,并用有限元法进行了验证,但并未对转子无铁心结构模型作进一步分析。
本文主要针对表贴式永磁电机转子无铁心的特点,结合电机电磁场的相关知识,利用麦克斯韦方程建立无转子铁心的解析模型,分析电机的气隙磁密、空载反电动势等参数,利用有限元法对解析模型进行了验证,采用解析建模的方法可为无转子铁心电机磁场的设计提供一种快速分析计算的方法。
1 表贴式转子无铁心永磁电机的结构
本文的表贴式转子无铁心电机为24槽8极,电机的额定转速设置为750 r/min。电枢绕组采用星形连接方式。在定子表面开有梨形槽,转轴采用具有非导磁性能的合金。永磁材料选用铁氧体。电机尺寸如表1所示。
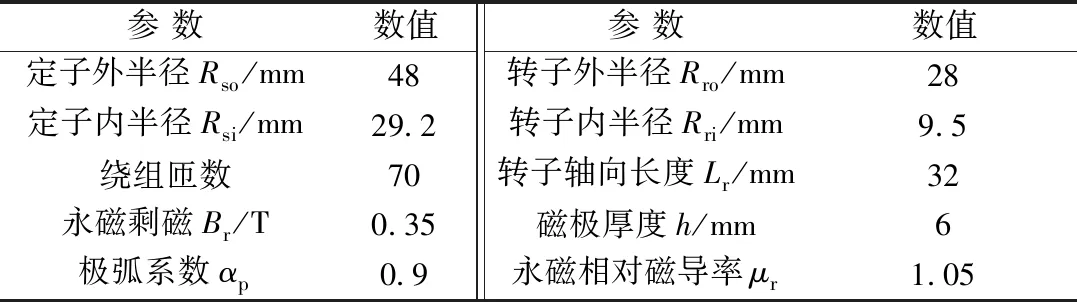
表1 电机的结构参数
电机的定转子结构如图1所示。
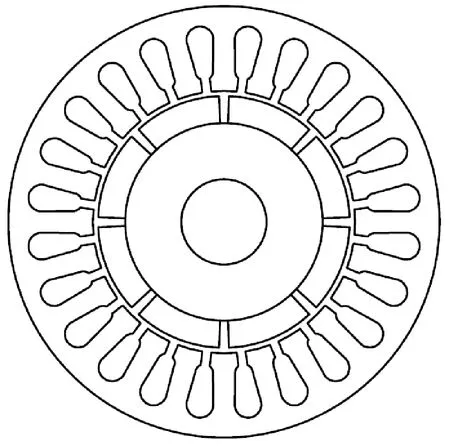
图1 电机整体结构
2 转子无铁心解析法建模
2.1 转子平行充磁分析
针对电机转子中的永磁充磁方式,结合相关文献,以及目前生产加工中相对成熟的工艺,电机转子中永磁体的充磁方式选用平行充磁方式,充磁方向如图2所示。
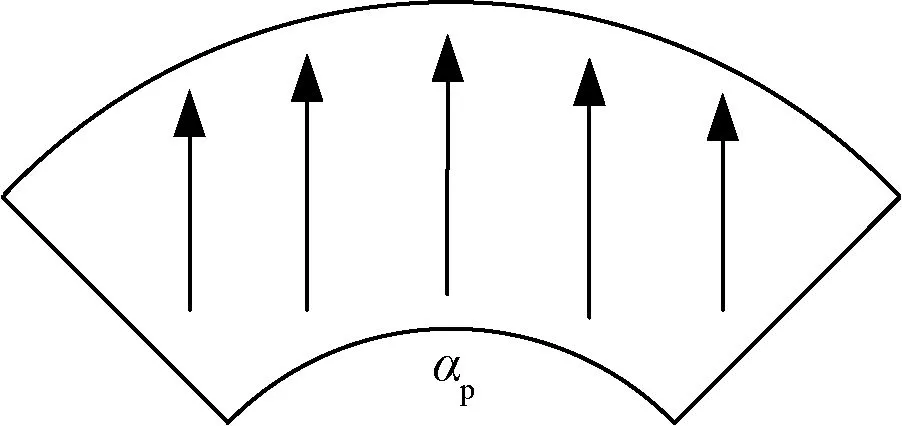
图2 转子平行充磁示意图
在一对极周期内,对平行充磁沿径向和切向方向作矢量分解,其中αp表示永磁区域在一个磁极中的有效占比。矢量分解结果为Mr和Mθ,Mr和Mθ分别为磁化强度沿着径向和切向方向上的分量。
(1)
(2)
(3)
(4)
(5)
从上式可以看出,Mr和Mθ的数值与转子所在的空间位置有关。
2.2 电机空载磁场建模
利用电机电磁场相关知识,首先假设电机定子内表面光滑,电机铁磁材料内部不存在磁密饱和,且定子铁心材料的磁导率假想为无穷大,转子永磁磁极采用表贴式瓦片形结构,永磁材料为平行磁化,且为线性退磁特性。
结合拉普拉斯方程和准泊松方程,根据电机磁场边界条件具有连续变化的特点,可将整个电机的区域划分为以下几个区域:电机气隙磁场区域Ⅰ,转子永磁体区域Ⅱ,转子无铁心区域Ⅲ。电机磁场划分区域如图3所示。
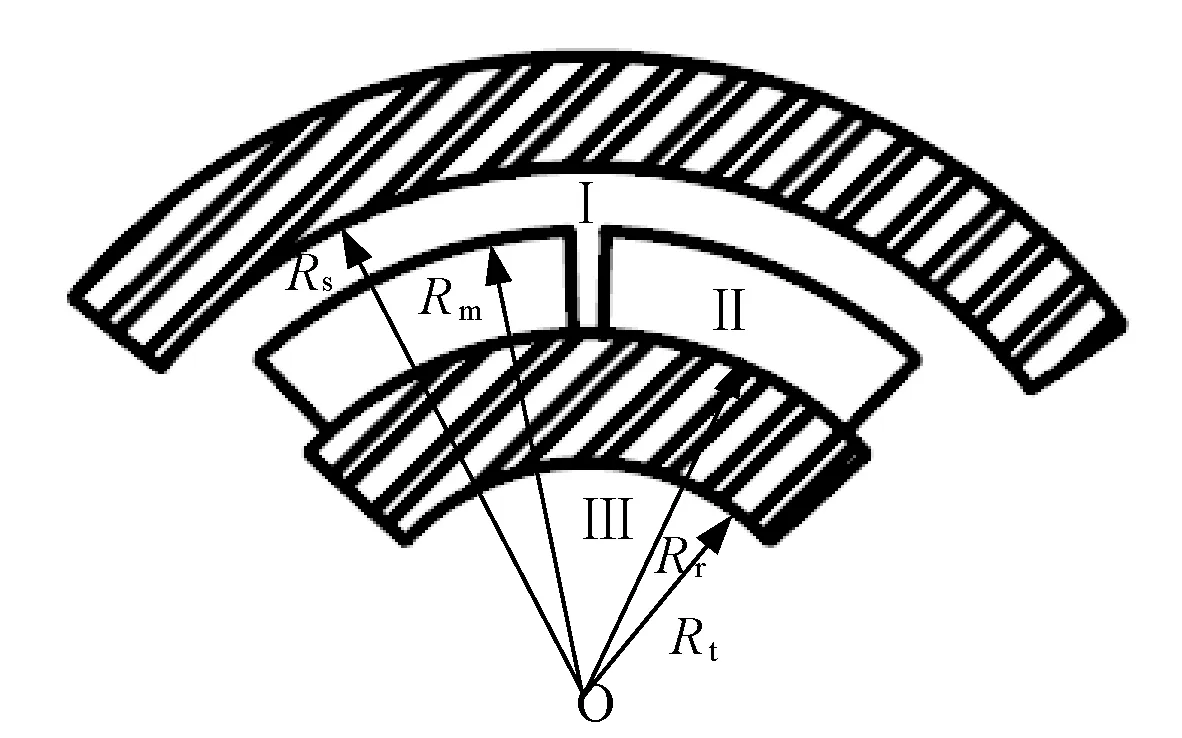
图3 磁场分析区域划分
在图3中,永磁体厚度是由Rm和Rr决定的,Rt表示铁心的半径,当Rt=0时,表示电机无转子铁心,Rs表示定子的内半径尺寸。
对于气隙区域以及永磁体区域,它们的标量磁位方程则有如下关系:
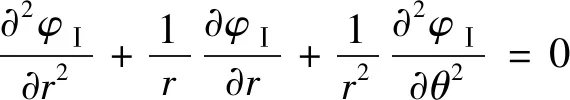
(6)
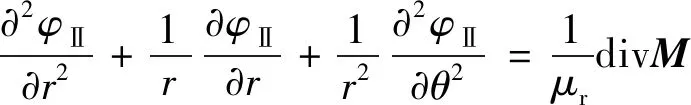
(7)

(8)
磁场强度H在径向和切向方向上的分量具有下列关系:
(9)
同时,将磁化强度M写成矢量分解求和的形式:
M=Mrer+Mθeθ
(10)
式中:Mr和Mθ分别为磁化强度沿着径向和切向方向上的分量。
磁场强度H与磁感应强度Br在磁场边界处需满足如下关系,
(11)
为便于计算,可将磁化强度分量写成级数累加的形式:
(12)
(13)
同时,将电机的转子磁极沿圆周对每一极进行划分,则每极占有π/p机械角度,由于一对磁极中包含N和S极,即存在下列关系:
(14)
进一步对磁化强度求散度计算,则满足下列关系:
(15)
结合上述微分方程及磁场的边界条件,联立后可得径向和切向气隙磁密表达式:
(16)
(17)
式中:

(18)
(19)
(20)
(21)
(22)
3 转子无铁心空载气隙磁场的分析
从图1中看出,电机定子结构部分开有梨形槽,定子内表面是非光滑连续,气隙磁密在定子齿尖处会发生畸变,造成磁密中的谐波含量增加,引发电磁噪声、电磁振动等问题。
在采用解析法分析表贴式永磁电机转子无铁心问题时,已假设定子内表面光滑连续。为了便于验证解析模型的正确性,采用有限元法对其进行验证,但在实际计算时,有限元法必须对电机模型作适当修改,简化为定子内表面光滑连续。
图4是采用有限元法获得的电机径向气隙磁密,分别分析了考虑定子齿槽效应和忽略定子齿槽效应(需对定子内表面作适当修改,保持定子内半径不变)两种情况。
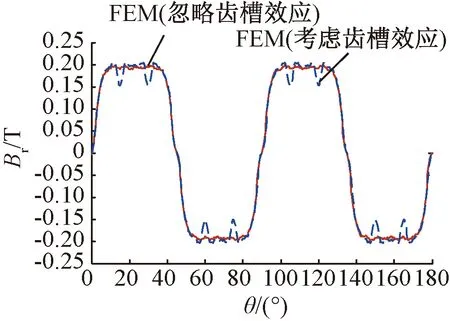
图4 考虑齿槽效应与忽略齿槽效应时有限元法获取的径向气隙磁密波形对比
从图4中可以看出,气隙磁密波形在定子开口处出现非光滑下凹的现象,发生了部分畸变。当忽略定子齿槽时,气隙磁密波形仍保持光滑连续。由此可以得出,定子开槽破坏了电机气隙长度的均匀性,由于铁磁导率远大于空气磁导率,磁密波形在接近定子槽口处磁通路径必然要发生一定的改变,造成气隙磁密波形中谐波成分的增加。
对图4的考虑定子齿槽效应以及忽略定子齿槽效应的磁密波形分别作FFT分析,如图5所示。

图5 空载径向气隙磁密FFT分析
从图5中可以看出,在定子开槽情况下获得径向气隙磁密基波幅值为0.233 3 T,总谐波为27.59%。当忽略定子齿槽效应时,定子内表面光滑,获得的径向气隙磁密基波幅值为0.236 9 T,磁场中的谐波含量占25.48%。对比分析可知,在电机定子结构上开槽,会降低磁密的基波幅值,增大THD。
同样,采用有限元法获得的电机切向气隙磁密如图6所示。
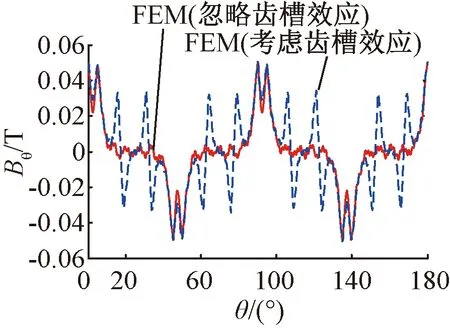
图6 考虑齿槽与忽略齿槽效应时有限元法获取的切向气隙磁密波形对比
从图6中可以看出,切向气隙磁密波形反映了定子齿槽结构的影响,定子开槽波形变化非常明显,主要是由于在定子各个齿尖处磁密中的切向分量变化比较迅速,加剧了磁场中的谐波含量。
上述分析都是基于有限元法,为了便于突出所建立解析分析法的准确性,以下分析选用忽略电机定子齿槽效应的结构。在电机参数完全一致的情况下,解析法与有限法获得的径向气隙磁密波形如图7所示。

图7 解析分析法与有限元法获得的径向气隙磁密波形比较
采用同样的分析方法,获得的电机切向气隙磁密波形如图8所示。

图8 解析分析法与有限元法获得的切向气隙磁密波形比较
从图7和图8中可以看出,对于电机转子无铁心结构模型,解析法与有限元法获得的电机径向、切向气隙磁密波形完全一致,验证所建立的转子无铁心电机空载磁场的解析法的准确性。
利用所建立的解析分析模型,仅改变表1中电机的极弧系数αp,永磁采用平行充磁,获得电机的径向气隙磁密曲线,并对其作FFT分析,磁密的基波幅值与THD随αp的变化规律如图9所示。
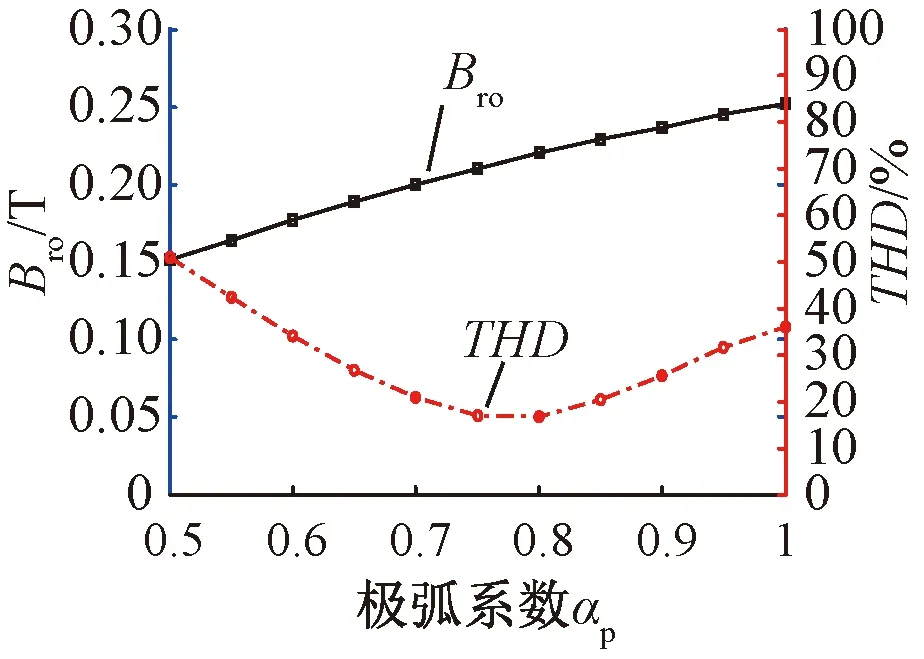
图9 磁密基波与THD随αp的变化规律
从图9中可以看出,径向气隙磁密的基波幅值随着极弧系数αp的增大而增大,总谐波THD随着αp的增大出现先减小后增加的趋势,当αp在0.75~0.8之前时可获得较低的THD。因此,电机在设计时选取合适的极弧系数可有效降低气隙磁场中的谐波含量。
从以上分析中可以看出,解析法相对有限元法具有快速计算的特点,在分析处理相关变量时非常简便,获取参数变化对磁密的影响也更清晰。因此借助解析法分析转子无铁心的空载磁场分布更具有优势。
4 空载反电动势分析
电机在空载场下相反电动势是反映电机电磁状态的关键参量,在电机设计时必须对其充分讨论。
根据电磁学相关知识,一个导电线圈所产生的磁通量[10-11]:
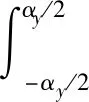
(23)
式中:αy表示为绕组的节距;l代表电机的轴向长度。
结合绕组磁链与相反电动势的关系可知:
(24)
Kdpn=Kpn·Kdn
(25)
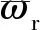
(26)
从绕组的相反电动势解析式中可以看出,相反电动势大小与线圈绕组的匝数、电机定子内径尺寸、转速、绕组因数、磁密幅值、电机轴向长度等参数有关。
采用解析法与有限元法获得的相反动势波形如图10所示。
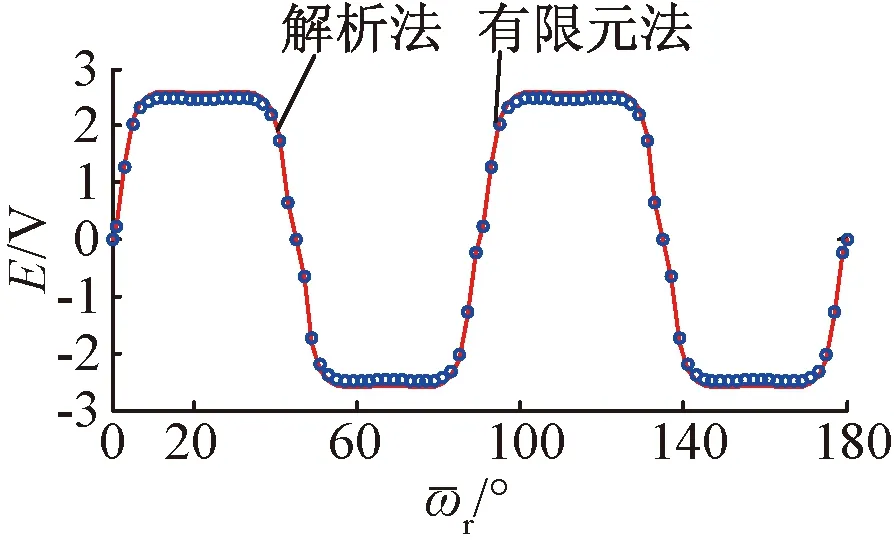
图10 解析法与有限元法获得的空载反电动势
从图10中可以看出,对于转子无铁心结构,解析法与有限元法对相反电动势的分析基本一致,但在曲线吻合度上稍有些差异,没有气隙磁密曲线的分析结果更精确。主要原因归于,作用在绕组中的磁势主要来源于磁密中的径向分量,转子在旋转过程中切割线圈,绕组也会受绕组分布系数、节距系数的影响,另外解析法在实际计算反电动势时,是由一系列级数累加而成,选取的多少会影响到曲线的逼近程度。但从整体变化趋势以及反电动势幅值可以看出,用解析法计算反电动势仍是可行的。
5 结 语
本文主要针对表贴式转子无铁心永磁电机结构,转子永磁采用平行充磁方式,借助有限元法对考虑定子齿槽效应以及忽略定子齿槽效应的电机空载磁场进行讨论。同时,为了便于解析建模,对电机磁场的边界条件进行简化,解析法在分析时忽略了定子齿槽效应的影响。研究结果表明,对于转子无铁心结构,采用解析法获得的径向和切向磁密波形与有限元法完全一致,在求解反电动势时与有限元法曲线的拟合度上存在细微差异,但对反电动势波形的幅值并无无实质的影响。相比于有限元法,解析法在改变电机参数变量获取相关变化规律时具有很强的时效性,因此在表贴式转子无铁心电机结构的设计过程中具有一定的实际应用价值。

